基于用户兴趣差异改进矩阵填充的个性化推荐算法

王志远 王兴芬

1(北京信息科技大学计算机学院 北京 100101)2(北京信息科技大学信息管理学院 北京 100192)

0 引 言

当今大数据时代面临的主要问题之一是如何从庞大的数据海洋中寻找到用户需要的信息，即信息过载问题。个性化推荐技术逐渐兴起，相比于信息系统、搜索引擎等技术，个性化推荐技术有着精准定位、因人而异的优点，它往往不需要用户搜索式地输入信息，而是通过用户的历史行为记录或历史评价信息为用户提供个性化的信息推送和智能决策。个性化推荐技术在很大程度上能解决传统搜索中的信息冗余问题，尽可能地避免用户浏览大量的无关信息和不感兴趣的信息，极大地提升了用户的体验。以往推荐算法的功能是在当数据中没有满足用户需求的信息时，向用户推荐尽可能接近用户需求的信息。而目前推荐算法需要解决的问题是，当数据中有大量符合用户需求的信息时，根据用户的历史数据推测出用户的潜在需求，然后根据用户的潜在需求进一步从数据库中筛选出用户可能需要的信息，排序后推荐给用户。这种潜在的需求可能是用户自身都没有察觉到的个人偏好，但它是真实存在的，就蕴藏在数据之中。

推荐技术的出现和不断成熟使得这些网络平台的内容提供商的个性化服务功能不断完善，用户的实际体验也逐步攀升，甚至对推荐系统产生依赖性，增加了用户的黏性，带来了巨大的经济价值。而对于广大的用户来说，一个高度智能的推荐系统不仅节约了大量宝贵的时间，快捷高效地获得想要的信息数据，而且极大地降低了寻找感兴趣的信息的难度。因此无论是对信息服务的提供商还是对于广大的普通用户，推荐技术的应用都有着其独特的重要意义。

1 研究现状分析

协同过滤算法是个性化推荐中使用最为广泛的方法，然而在用户和项目的数量十分庞大但是用户只在很少的项目上有评分记录时就会导致数据稀疏性问题。在协同过滤算法中，数据稀疏会使得用户之间计算相似度时可以用来进行计算的数据过少，导致求得的用户相似度不准确，最终影响预测评分的准确度。

针对协同过滤中存在的数据稀疏性问题，国内外学者进行了大量的研究。在融合多源数据方面，王建芳等[1]针对用户交叉评分项较少的情况，提出一种相似度与社交网络中信任因子结合的协同过滤算法，在对评分矩阵填充时存在误差的项目通过信任因子动态调整，获得更符合实际的相似度；万惠等[2]根据社区划分的思想，采用凝聚式层次聚类算法对电影类别划分为不同的社区，在目标用户所属的社区里通过用户的标签和评分数据计算用户间的相似度，进而对目标用户进行推荐，提高了推荐的效果；肖成龙等[3]融合社交网络和关键用户信息，在用户-项目矩阵的基础上得到了社交信任矩阵和关键用户评分矩阵，然后分别赋予这三个矩阵不同的权重，协同计算出用户对目标项目的预测评分，有效地缓解了数据的稀疏性问题。在矩阵分解方面，李晓菊等[4]提出了一种基于变分循环自动编码器的概率矩阵分解方法,将商品的描述文本编码成一个特征向量,然后将该特征向量融合到概率矩阵分解模型中,在评分矩阵极其稀疏的情况下,能更有效地预测用户感兴趣的商品列表,提高推荐准确性；毕闰芳[5]提出了一种基于SVR的矩阵填充模型，首先通过对原始的用户评分矩阵中的空缺值使用预测值填充，然后采用协同过滤算法形成初步的推荐列表，最后借助用户兴趣偏好画像对推荐列表进行二次筛选；罗国前等[6]通过融入情境偏置和全局偏置在矩阵分解算法的基础上对目标项目预测评分，一方面使得矩阵规模大大下降，另一方面通过情境因素对预测评分的修正，提高预测的准确度；蔡念等[7]通过加入用户和项目的影响因子改进传统的矩阵分解模型，同时与跨通道卷积神经网络结合，提高了预测模型的准确度。在融合多模型方面，于欢[8]采用多模型融合的算法深层次提取了用户的偏好，同时重点关注用户的近期偏好，使得模型在推荐结果的准确度和惊喜度上更加灵活，为不同用户提供的推荐更个性化，有助于进一步提升用户的真实体验；胡芳燚[9]全面分析了用户评分所造成的全局影响，并且利用物品相似度与用户之间的映射关系提高了用户间相似度计算的准确性，同时根据用户评分时间通过引入艾宾浩斯遗忘曲线调整评分数据的权重，挖掘用户的兴趣变化规律，分析群体性行为对用户兴趣偏好的影响；汤颖等[10]针对传统的推荐算法难以捕捉用户兴趣偏好的问题，设计了一种基于用户局部模型加权融合的算法，该算法借助LDA主题模型于语义层次计算用户的特征向量实现用户聚类，进而提高了电影的个性化推荐效果。

以上改进研究在一定程度上提高了推荐的效果，但没有充分挖掘分析在实际应用场景中用户属性和项目内容相较于其他领域的特殊性及其对推荐结果的影响。本文聚焦于电影推荐领域,针对协同过滤算法只考虑用户评分而忽略用户属性和项目内容的缺点，研究不同用户的兴趣差异，在对用户未评分项目进行预测时，着重分析了用户兴趣差异和项目属性对预测结果的影响。经过在电影评分数据集上的实验验证，本文算法在数据稀疏的情况下仍能保持预测评分的准确度，有效地提升了算法的推荐性能。具体的算法模型如图1所示。

图1 改进矩阵填充的推荐算法模型

2 优化项目选取的矩阵填充算法

把不同用户对商品的评分数据转化为用户-商品矩阵，每一行为一个用户，每一列为一个商品，矩阵的每一个取值为该行对应用户对该列对应商品的评分，若无对应评分则为空值。但是因为商品数量众多，对于每个用户来讲，他所评价过的商品只占所有商品很小的一部分，所以生成的用户-商品矩阵是极度稀疏的。KNN算法的假设是：喜欢相似物品的用户具有相似性，在商品推荐中即为对商品有相近评分的用户具有相似性，有相近评分的商品越多两位用户的相似度越高。所以通过KNN算法计算得到的相似的用户往往在两者的商品评分列表中需要有足够的交集。这就导致有许多相似用户因为相交部分过少甚至没有相交部分而被忽略，但是这种情况会随着用户有评分的商品的数量的增加而减少。因此本文对用户-商品矩阵进行填充，降低用户-商品矩阵的稀疏程度，推高商品推荐的准确度。

2.1 基于关键词的相似度计算

在经典的Slope One算法中，每一个被填充的项目的分值都受到所有其他项目的影响，然而实际上其他项目可以分为与被填充项目相似的项目和无关的项目两部分，如果能准确地将其划分，那么一方面可以大大减少许多不必要的计算量，提高矩阵填充的速度，另一方面，由于减少了无关项的干扰，也可以使预测评分的准确度得到提高。因此，在采用Slope One算法进行矩阵填充之前，要先计算出不同项目之间的相似度。

在计算电影之间的相似度时，若以电影的标签为基准则颗粒度过于粗糙，只能笼统地分为几类或是十几类。所以，为了提高电影的相似度计算结果的精度，本文采用了电影的关键词数据来进行计算。表1展示了部分数据的关键词，可以看出，电影的关键词对电影的主题以及包含的元素都有较为细致的体现，因此通过对关键词的计算可以衡量不同电影之间内容的相似度。

表1 电影关键词表

在本文使用的数据集中，每部电影有10个左右的关键词，关键词满足约束条件：每个关键词仅包含一个明确语义，不同关键词语义之间可以有交叉，但不完全重复。以上约束可以保证，两个关键词的语义越相似则相关度越大。将所有的关键词k组成一个集合K，每一部电影对应的全部关键词看作一个事件T，则每个事件都是项集的一个子集。统计所有的事件T中不同的ki和kj共同出现的频数，计算ki和kj的相关度cori,j，表示为：

(1)

两部电影之间的相似度frei,j，即为这两部电影的关键词列表中相关度最高的前m项的平均值，计算式如下：

(2)

2.2 基于选择倾向度的用户聚类

用户在选择商品时，往往会对某一类或某几类的商品情有独钟，在选择电影时也是如此，即当用户在选择看电影时有对电影种类的倾向性。同时，当用户给某部电影一个很低的评分时，事实上对于这位用户而言，他已经给这部电影投过赞成票，也就是说在没有观看之前，他对这部电影是感兴趣的。据此可以推断出用户对这类型电影的标签是感兴趣的，但是由于这部电影本身的质量不佳或与该用户的预期不符导致最终该用户对这部电影的评分不高。因此，虽然用户对电影的评分很直观地反映出了该用户对这部电影的最终评价，但仍可以通过对其行为规律的挖掘，找到隐藏在评分背后的用户兴趣倾向。用户对电影类型的选择倾向度计算式如下：

(3)

式中：I为电影的类型集合；NA,i为用户A观看过的i类电影数；treA,i为用户A对i类电影的选择倾向度。计算出每位用户对不同类型的电影的选择倾向度之后，得到了一个用户—电影类型矩阵，矩阵中的每个值为对应用户对相应电影的选择倾向度。矩阵的结构如表2所示。

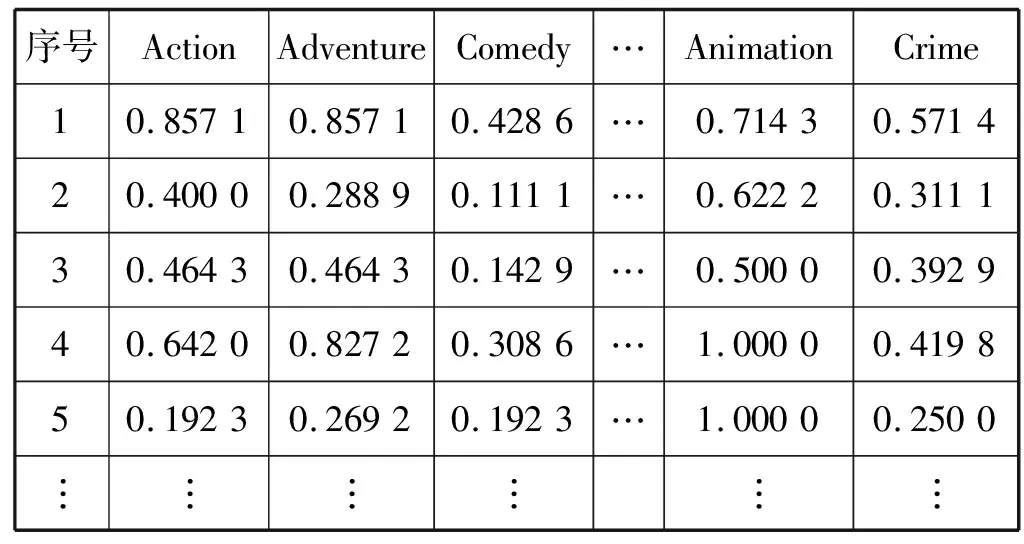
表2 用户选择倾向度

表2中的每一行代表不同用户，每一列代表不同的电影类型，共有二十种，分别为：Action，Adventure，Animation，Comedy，Crime，Documentary，Drama，Family，Fantasy，Foreign，History，Horror，Music，Mystery，Romance，Science Fiction，TV Movie，Thriller，War，Western。基于这个矩阵，就可以根据用户对不同类型电影的选择倾向度采用k-means聚类算法将用户聚类。

k-means聚类算法是基于划分的聚类算法，使用最为广泛，有着简单准确的优点，在各领域备受欢迎。其基本思想是，通过度量不同点之间的距离，迭代地调整聚类中心的位置，直到中心点的位置变化差值小于某一阈值。经典的k-means算法的缺点是选取聚类个数和聚类中心具有盲目性，使得聚类结果容易收敛到局部最优解并且收敛速度缓慢。考虑到在协同过滤算法计算用户相似度时，两名用户都有评价的项目越多，计算结果就会越准确。因此，结合用户相似度计算的特殊性在采用k-means算法选择初始的聚类中心时，首先筛选出评分数据中评分数量最多的极小部分用户，计算他们的相似度，然后采用两两之间相似度差值最大的k位用户作为初始的聚类中心。在选择聚类个数的时候，可以通过多次实验对比结果的办法，找到效果最佳的聚类个数。

2.3 填充用户-项目评分矩阵

Slope One算法最早由Daniel Lemire教授于2005年提出，该算法假设两个项目的评分之间存在线性关系，只要计算出两项目的评分的平均偏差以及两位用户的评价尺度偏差，就可以计算出对某项目的预测值。用户对项目的评分用矩阵Rm×n表示，Ru,i为用户u对项目i的评分，Iu为用户u的所有评分项目，Ui为对项目i有评分的所有用户的集合，Ui,j=Ui∩Uj为对项目i和项目j都有评分的用户的交集，Ni,j为集合中元素的个数，则项目i和项目j之间的评分偏差Devi,j以及目标用户x对项目i的预测评分prex,i的计算公式为：

(4)

(5)

经典的Slope One算法简单高效并且易于扩展，但是没有考虑到用户的兴趣偏好和项目的内容之间存在的相似性，随着数据规模的不断增大，会导致内存占用大、运算效率低并且预测结果的准确度也会变低。因此，利用前面得到的基于选择倾向度的用户聚类结果和电影的相似度计算结果，在对用户-电影评分矩阵进行填充时，只使用同类型用户中与待填充项相似的电影评分进行计算，可以大大减少预测某一评分时所需的其他评分数据量，提高系统的运行速度。另外，只采用同类用户和相似项目的评分进行预测，可以使预测更加准确更有说服力，同时提高整个推荐系统的个性化程度。

3 基于用户偏好修正的协同过滤算法

协同过滤是推荐系统中被最广泛采用的推荐方法，它大致可以分为三类：基于用户的协同过滤、基于项目的协同过滤和基于模型的协同过滤。本文采用基于用户的协同过滤算法，它基于与某用户相似的用户喜欢的物品该用户也会喜欢的基本假设，通过对用户的历史数据进行分析，找到与该用户最相似的用户群，然后根据该用户群里的其他用户对项目的评分情况，找到该用户可能感兴趣的项目。

3.1 相似度计算方法

基于用户的协同过滤首先要计算用户之间的相似度，主流的相似度方法有欧式距离、皮尔逊系数、余弦相似度以及它们的变种。在电影推荐系统中，皮尔逊系数往往比其他计算方法更为有效，因为皮尔逊系数在计算相似度时充分考虑了不同用户的评价准则不同对相似度计算结果的影响。在经过多次对比实验，在其他条件都相同时，基于皮尔逊系数的相似度有较小的MAE值，且较为稳定。在计算某两名用户的相似度时，只需要把他们共同评价过的n部电影取出来，用对应的评分值作为这n维向量每个维度的值，即可根据公式计算两向量的皮尔逊相关系数得到两位用户的相似度。

(6)

由于对于每个用户来说，有评价的电影只占很小的一部分，将所有用户的评分转化为用户-评分矩阵是极其稀疏的。同时，利用皮尔逊系数计算出的相似用户的必要条件是两位用户都有评分的电影有足够大的交集，若都打过分的电影数量不足时，计算出的相似度就会不准确。因此，本文采用矩阵填充的方法，将用户对电影的预测评分插入评分矩阵中，拓展用户向量的维度，弥补交集数量不足的影响。但是预测评分往往和真实评分之间存在误差，而用两个有误差的数据进行计算显然会造成误差的累积。因此，首先找到两位用户有真实评分的电影集合的并集，然后对并集中没有某一用户评分的电影采用对应的预测值进行补全，最后用补全后的集合计算两位用户的相似度。

3.2 形成Top-N推荐列表

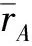
(7)

根据电影的标签，将A对电影的评分转化为对标签的评分，得到A的偏好列表。然后根据电影m的标签，修正用户A对电影m的评分预测值：

(8)

式中：rA,g为用户A对电影m对应的标签g的偏好值,α为修正系数，修正系数的取值为使得真实评分值与类型标签加权后的评分预测值间的平均误差ε取得最小值时的权重系数。具体的计算公式如下：

(9)

式中：Num为该用户的评价电影数。

改进后的协同过滤算法步骤如下：

输入：用户A，评分矩阵Rm×n。

输出：针对用户u的Top-N推荐列表。

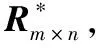
Step3根据最近邻居集UA里用户的评分，利用式(7)计算出用户A对待预测项目的预测评分。

Step4利用式(8)对用户A的预测评分进行修正，将修正评分后的项目降序排列，把前N个项目推荐给用户A。

4 实验结果及分析

本文的实验数据来源于Kaggle网站上的The Movies Dataset，在该数据集中包括270 000位用户对超过45 000部电影的约2 600万条评分数据，根据式(10)计算出数据的稀疏度为1-26 000 000/(270 000×45 000)=0.997 8。

(10)

式中：spares为矩阵的稀疏度；Nr表示总评分数；Nu表示数据包括的总用户数；Ni表示数据包括的总项目数。

该数据集包括了5个数据文件：存储包括海报、背景、发布日期等元数据信息的文件movies_metadata.csv，存储电影情节关键词信息的文件keywords.csv，存储演员和制作人员信息的文件credits.csv，存储所有评分数据的文件ratings.csv，以及该数据集中所有电影对应的TMDB id和IMDB id文件links.csv。在实验中采用五折交叉法进行验证以避免偶然性，将数据集中每位用户的评分数据随机分为大致均匀的5份，每次实验取其中4份为训练集，剩余的1份为测试集，经过独立的5次实验后，取结果的平均值作为最后的实验结果。

4.1 用户聚类结果

对聚类的效果进行评判的标准一般为各个样本之间的距离或相似度，对于聚类生成的不同簇来说，将簇内的距离或相似度称为凝聚度，将簇间的距离或相似度称为分离度。通常簇内距离越小或者相似度越高则凝聚度越大，反之则越小；簇间距离越大或者相似度越低则分离度越大，反之则越小。然而凝聚度和分离度两者并不独立，其和等于每个样本到总均值距离的平方和，因此不应该单独地使用凝聚度或分离度作为聚类效果的评价标准，在本文中采取结合了凝聚度和分离度的轮廓系数作为聚类效果的度量标准。

轮廓系数的计算可以分为以下两步：

第一步计算样本个体的轮廓系数，假设样本di被划分到簇A中，ai为该样本到它所属的簇中其他所有样本的平均距离(体现凝聚度)，bi为该样本与不包含它的任意簇中其他所有样本的平均距离(体现分离度)，则该样本的轮廓系数silhouettei的计算公式为:

(11)

第二步计算这次聚类结果的平均轮廓系数silhouettek，n为样本的总数，k为聚类的个数，则silhouettek的计算公式为：

(12)

样本的轮廓系数可以衡量该样本划分的匹配程度，其取值silhouettei∈[-1,1]，值越接近1表示该样本与它所属的簇内的其他样本越相似，越接近0表示该样本越靠近簇的边缘，越接近-1则表示该样本更应该被分到其他的簇中。平均轮廓系数silhouettek可以用于评估本次聚类的效果，通过比较所有可能的分类个数，取其中silhouettek最大的分类数k为最终的聚类个数。

本文对用户可能的聚类个数进行实验，得到选择不同聚类个数k时的轮廓系数走势，如图2所示。可以看出，聚类结果的轮廓系数随着聚类的个数增多有下降的趋势，在等于2时取得最大值，但只是简单地将用户分为两类并不能将用户的兴趣偏好多元化地呈现出来，因此考虑第二个波峰，即聚类个数等于5或6的情况。由于后续的步骤中会在不同兴趣偏好的用户群组的内部进行计算，又希望不同群组中包含的用户数量尽可能均匀，因此参考不同聚类个数下的方差，经计算在聚类个数为6时簇内方差的平均值比聚类个数为5时小。综合以上两点考虑，本文选取的聚类个数k为6。

图2 不同聚类个数时的轮廓系数

4.2 矩阵填充结果

Slope One算法的实质是预测用户对某一个项目的评分，它依赖于用户与用户评分尺度的差值以及项目与项目之间平均评分的差值，有着准确率高、易于实现的优点。但传统的Slope One算法存在盲目性，它并不对参与预测计算的值进行筛选，对于某两位兴趣偏好截然不同的用户或者某两个内容毫不相关项目显然并没有可比性，使用所有数据进行计算一方面会使计算量比较大，另一方面数据来源并不精准会导致预测结果的个性化程度降低。

传统的Slope One算法可以根据用户-项目评分矩阵对矩阵中绝大部分的空缺值计算出预测值，但是本文在这一步中的目标并不是计算出所有空缺值的预测评分，而是希望降低用户-项目评分矩阵的稀疏程度。因此利用用户以及项目之间的相似度对Slope One产生的预测值数量进行限制，在预测精度与预测数量之间进行取舍，将高准确度的预测值填充进用户项目矩阵。

根据式(5)，对于某一待预测的项目添加限制条件：待预测项目和与它相似项目的共同评分用户数量需大于阈值Nu。通过对阈值Nu进行调整即可控制预测评分的数量，根据不同的阈值计算出填充后的矩阵稀疏度如图3所示。可以看出，当阈值取8时矩阵的稀疏度为0.952 3，最接近理论值，因此本文选择将Nu=8时计算出的预测值填入用户-评分矩阵。原始数据对应的用户-评分矩阵的稀疏度为0.997 8，填充后对比原始矩阵的稀疏程度降低了(1-0.952 3)/(1-0.997 8)=21.68倍，有效地降低了评分矩阵的稀疏度。

图3 阈值与矩阵稀疏度的关系

4.3 推荐效果

个性化推荐算法性能的指标非常丰富，不同的指标侧重于推荐结果的不同方面，主要有覆盖率、多样性、新颖性和惊喜度等。而对于离线实验往往采用评分预测准确度来进行衡量，常用的指标主要有平均绝对误差和均方根误差。

平均绝对误差MAE和均方根误差RMSE都是根据用户的实际评分值和预测评分值来进行误差度量的，MAE或RMSE的值越小则评分的预测值越准确。假设P为用户的预测评分集合，R为用户的实际评分集合，pi和ri为某用户对某一电影对应的一组评分预测值和真实值，pi∈P且ri∈R，N为数据集中的评分总数，MAE和RMSE的计算公式如下：

(13)

(14)

本文选择平均绝对误差MAE和均方根误差RMSE作为评分预测准确度的度量指标，从现有方法中挑选了最具代表性的SVD++[12]、NNMF[13]、FML[14]3种方法作为基线，与本文提出的方法分别在MovieLens 100k数据集[11]和The Movies Dataset上进行对比实验。

1)SVD++：在考虑用户和商品偏差项的矩阵分解模型的基础上引入了隐反馈。

2)NNMF：使用多层感知机来对用户和商品间的关系建模，实验中使用了4个隐藏层。

3)FML：引入了度量学习对用户和商品间的关系建模。

MovieLens 100k数据集是电影推荐领域最常用的数据集，它包括来自1 000个用户对1 700部电影的100 000个评分，根据式(10)计算得出其稀疏度为0.941 2，The Movies Dataset的稀疏度为0.997 8，是前者的(1-0.941 2)/(1-0.997 8)=26.73倍。

最近邻的个数k也是影响推荐结果的一个重要因素，实验一将本文算法SFCF与其他3种算法在MovieLens 100k数据集上比较，结果如图4所示。可以看出：随着最近邻数目增大，各算法的MAE值都迅速下降，当超过某个值时，会趋于稳定并有一定波动。以SVD++算法为例，在最近邻数目40左右时MAE取得最小值，之后会有明显回升，其他2种算法与它类似。而本文提出的SFCF算法在最近邻数目增大时较为稳定，起伏不大，说明填充后的矩阵中每位用户的相似用户数目较多，不会因为相似用户数目过多而导致选取低相似度用户进行评分预测计算，有效地保持了预测评分的精度，这一特性也符合为解决数据稀疏性而对评分矩阵进行填充的效果预期。

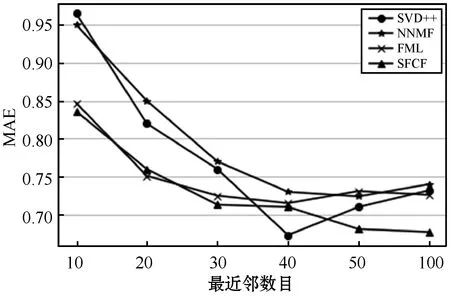
图4 4种算法随最近邻数目变化对比

实验二将本文算法SFCF与其他3种算法分别在MovieLens 100k数据集和The Movies Dataset上进行对比实验，结果如图5和图6所示。

图5 4种算法在MovieLens 100k的MAE和RMSE对比

图6 4种算法在The Movies Dataset的MAE和RMSE对比

通过对比可以看出在数据相对稠密的数据集MovieLens 100k上，本文算法的MAE和RMSE均比NNMF算法和SVD++低，与FML算法基本相同。但在数据更为稀疏的The Movies Dataset上，本文算法的MAE和RMSE均低于其他3种算法。同时，当数据的稀疏性增大时，其他3种算法的准确度都有大幅度下降，而本文算法仍能保持较高的准确度，证实了本文算法通过深入分析用户和电影的各维度属性数据，将挖掘出的不同用户的兴趣差异与协同过滤算法结合，有效地缓解了数据稀疏性问题对协同过滤算法的影响。

5 结 语

本文针对经典的协同过滤算法由于数据的稀疏性导致的推荐结果质量下降的问题[15-17]，提出一种基于用户兴趣差异改进矩阵填充的个性化推荐算法。首先利用优化项目选取的Slope One算法对用户-评分矩阵进行填充，然后使用填充后的矩阵形成Top-N推荐列表，最后根据用户的兴趣偏好对推荐列表再次过滤，得到最终的推荐结果。实验通过与其他协同过滤算法的比较，验证了本文算法可以缓解数据稀疏性的问题，在数据规模及其稀疏性不断增大的情况下，能有效地提高系统的推荐质量。本文提出的推荐算法在计算用户和项目的相似度时还有提升空间，在下一步的研究中，将考虑更多的用户的年龄、职业、地域，以及电影的导演信息、演员构成等更多维度的数据，以提高用户以及项目的相似性度量结果，从而提高最终的推荐质量。