基于相似性的社交网络结构建模

马 翔 徐名海 吴宇鹏

(南京邮电大学江苏省无线通信重点实验室 江苏 南京 210003)(南京邮电大学通信与信息工程学院 江苏 南京 210003)

0 引 言

社交网络是一种特殊且广泛存在的复杂网络[1]，社交网络结构建模是社交网络众多研究方向的基础研究领域，社交网络模型的合理性直接影响基于其上的其他相关领域研究成果的可靠性。在当今社交模式高度网络化时代，社交网络的研究是具有实用价值和重要理论意义的，社交网络建模可以挖掘社会网络中的关系，有效地模拟各种社会行为，更好地明白和解释各种社会现象包括信息传递、病毒传播、谣言传播等，它能从各个方面协助人们更深入理解真实世界。但由于社交网络具有很多动态性的结构特征以及无法对社交网络特殊对象做实验，研究面临着如何定义和衡量节点链接关系相关的重大障碍。例如，估算社交网络的主要工具是使用各种调查或对相关方的访谈。鉴于每个人有数百甚至数千个社交关系，让他们以任何所需的准确度回忆相关的人是很困难的。此外，可能无法联系或观察网络中的所有节点，并且在联系时，他们可能有理由扭曲或隐藏关系。即使是最近对网页、共同作者、电子邮件和引文网络的研究，虽更容易获得其中数据，但也忽略了其他测量特性。此外，社交网络随着时间的推移不断变化，并以各种方式重叠，亲密的朋友可能无法长时间互动。关于社交网络结构的大部分信息来自对链接的有限测量，这些链接通常采用静态和离散的视图，而这些视图本质上是动态的和易变的。所以有必要通过其建模来探究社交网络的演化，而如何构建逼近真实社交网络的结构模型是具有挑战的。

目前学术界对社交网络结构建模的研究相对较少，现有的研究主要从单一的网络特征来建模或从大数据的统计特性来说明社交网络，但这些方法具有一定的缺陷。从宏观角度来看，大数据是用软件工具捕捉收集到的一系列数据集合，所以由大数据得到的各种社交网络拓扑结构和各种特性具有后验性，其对于社交网络在信息传递的预演无能为力。从微观角度来看，社交网络的拓扑结构呈现是由多种因素驱使的，单一特征不足以说明其演化的特性。

针对上述问题，本文创新性地提出了一种相似网络模型。首先通过分析网络中节点间的各种活动行为、节点的个性特征，对用户行为相似度及特征相似度进行量化，将量化结果作为节点外部生长链接边的概率；然后根据网络结构影响完成内部演化；最后从度饱和的角度不停地更新网络链路。

1 研究背景

许多学者们为了能够更好地解释和模仿社交网络的生成规律和演化规律，纷纷提出各种方法模型试图来构建符合现实世界特征的社交网络。1998年，Watts等[2]提出了小世界网络模型，该模型基于现实世界中人们有相同数量朋友的假设，其度分布为泊松分布且峰值取平均值，平均路径短且聚集系数大。1999年，Barabasi等[3]提出了一种增长模型(BA无标度模型)，通过加入新的节点来实现网络的连续增长，而这些新的节点总是倾向于连接已经拥有大量连接的节点，他们应用了优先附着的概念，其中新节点以非均匀概率附加到网络图。文献[4]提出的最近邻模型中，新节点i连接到随机节点j和i周围的两跳邻居的随机对，可以对模型进行参数化来确定节点的数量及其连接的概率。Bodine-Baron等[5]提出了基于格的网络模型，该模型在任何具有足够小的距离依赖连接概率时的度分布服从泊松分布，并且这种网络具有可搜索性。Newman[6]分析了科学合作网络，发现两个节点熟悉的可能性随着他们共同的合作者数量的增加而增加。近年也有研究从社团结构[7]、优先连接与三角结构[8]来构建社交网络模型。

这些网络模型虽然捕获了社交网络的基本属性，但其仍然忽视了一些社交网络中存在的关键属性，因此有必要进一步研究与现实世界更为一致的社交网络结构特征。社交网络的相似性属性在真实世界中是具有广泛实践背景的。从心理学上来说，节点总倾向于与自己行为活动、个性特征相同的节点认识，他们的链路连接率比两个个性不同、活动不同的对象连接率更高，这说明了节点在社会网络中的连接有可能是基于某种相似的性质，节点与节点之间是由于存在某种共同的特性才相连。从历史的演进来说，社交网络的超稳定是基于网络结构一些相似的特征，网络的结构背景在网络演化过程中会促使节点间边的建立与断开，节点间边的断开和新建又促使网络不停地变化，但总体上各个时期的网络结构是相似的。近年，学术界的关注焦点转向了复杂网络的相似性。文献[9-11]证明了不同的局部网络可以覆盖不同的边框，来揭示复杂网络的自相似性，并使用盒子计数来统计复杂网络的自相似性。还有许多研究人员从历史位置[12]、节点影响力[13-14]、节点行为[15-16]和节点邻居[17]来分析研究并计算节点的相似度。但是鲜有学者从相似性和网络结构影响来探讨社交网络建模。本文就社交网络广泛存在的相似性提出一种基于相似性与网络结构的社交网络建模方法，本文所提出的相似性概念基于节点的内在属性与外在行为活动。每个节点有自己活动范围和个性特征，节点的相似性由这些节点间属性重合集合决定，两个节点的某种相似度特征越高，则这两个节点越有可能建立边的关系。相似性是社交网络中存在的重要属性，它不是偶然的，它应该发生并始终保持在网络演化的进程中。因此建立并研究基于相似性网络演化模型有利于更好地认识现实世界中的社交网络。

2 相似网络模型

复杂网络的相似性属性在真实世界中具有广泛的实践背景，人们总是乐于与那些在各个方面都与自己相似的人交朋友，类似于多米诺骨牌效应。社交网络的节点并不总是异质的，在许多方面都表现了相似的特征。本文所提出的相似网络模型是基于相似性的，并考虑网络结构影响，如果两个节点行为相似和特征相似大于相似度阈值，则其建立连接并形成复杂网络的相似特征。要计算节点的相似性，必须选择相关的节点属性，对于节点间的相似性，我们从节点的内在属性与外在行为活动来考虑。对于外在行为活动主要考虑签到集，内在属性主要考虑节点个性，而网络结构则在整个网络演化过程中影响网络链路的刷新。

2.1 社交网络相似性原理

每个活跃用户在不同位置聚类上有不同活动程度的行为模式，一个用户的外出位置一定程度上反映了该用户的活动行为，用户间所在位置相同的概率越大，用户就越有可能认识。本文在基于位置的社交网络中，组合节点所在物理位置与线上虚拟地点来探究用户活动，通过将位置集群与用户签到相结合来挖掘个人外在的行为模式，然后基于个人用户的所有签到集，计算用户之间的行为相似性。如图1所示，网格代表了不同的位置，用户可在不同的位置活动，当两用户所处同一位置越多时，行为相似度越高。

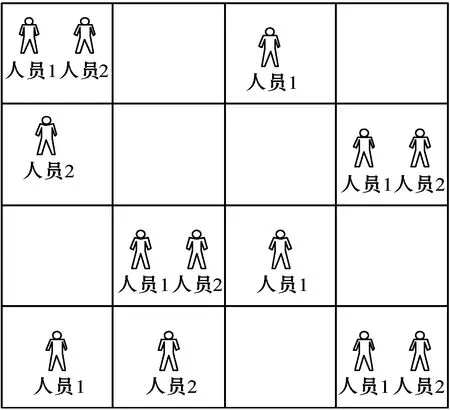
图1 用户位置活动

定义1在不同位置集群中各个节点的活动行为称为签到集。

节点A与节点B的行为相似定义在位置活动的一致性，则节点A与节点B的行为相似性表达式为：

(1)

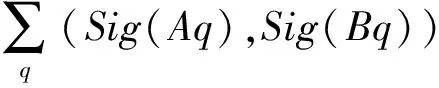
用户的内在属性主要表现在节点的个性特征上。一个用户的内在属性决定他的网络圈，也决定了他在信息传递过程中所参与的互动性，个性相同的用户更乐意在一起交流，传递信息。若两个对象存在共同的内在属性，则定义两个对象具有特征相似，其表达式为：

(2)

式中：C表示节点个性集合；Ci⊂C；C(A)表示节点A的共有多少种个性选择；Ci(A)表示节点A个性为Ci；Ci(A)×Ci(B)表示节点A与节点B个性相同都为Ci。如果两个节点具有相同的个性特征，则他们比两个个性特征不同的对象更相似，更倾向于建立连接。

2.2 网络结构的背景影响

构建社交网络模型，除了考虑节点的特征外，还需考虑社交网络结构的背景影响。对于单个节点周围的网络结构从节点邻居切入，对于大规模的网络结构从群结构切入。一个用户在网络结构中所受到的影响与其邻居密切相关，用户拥有共同的邻居结构，受到的影响越相似，用户越有可能建立连接。网络拓扑在一定程度上能够反映出节点之间的连接关系，如图2所示，当两个节点拥有多个相同的邻居结构时，他们会倾向于建立连接，其中图2(b)新出现的边代表两个节点基于拥有多个共同的节点建立的边关系。

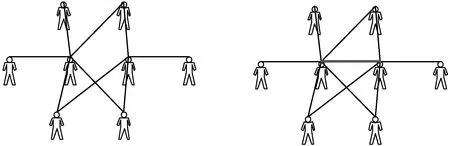
(a) (b)

社交网络大规模的结构背景在网络演化过程中会促使节点间边的建立与断开。当信息在社交网络中传输时，会促使一些节点形成群结构，如果两个节点在同一个网络群范围内接收相同的信息，则两个节点受到网络结构推动的影响，会相互建立连接。图3展示了群结构的形成，信息传输促使节点形成群结构进而推进节点间边的建立。社交网络群结构在演变时，一些节点会在不同的群结构中来回切换并扮演不同的角色，那些微交互的节点在群结构的变化中更容易受到影响进而断开连接。图4展示了节点边的断开，网络群随着时间的推移而变化，弱连接的节点容易断开连接，转而与其他节点建立连接。

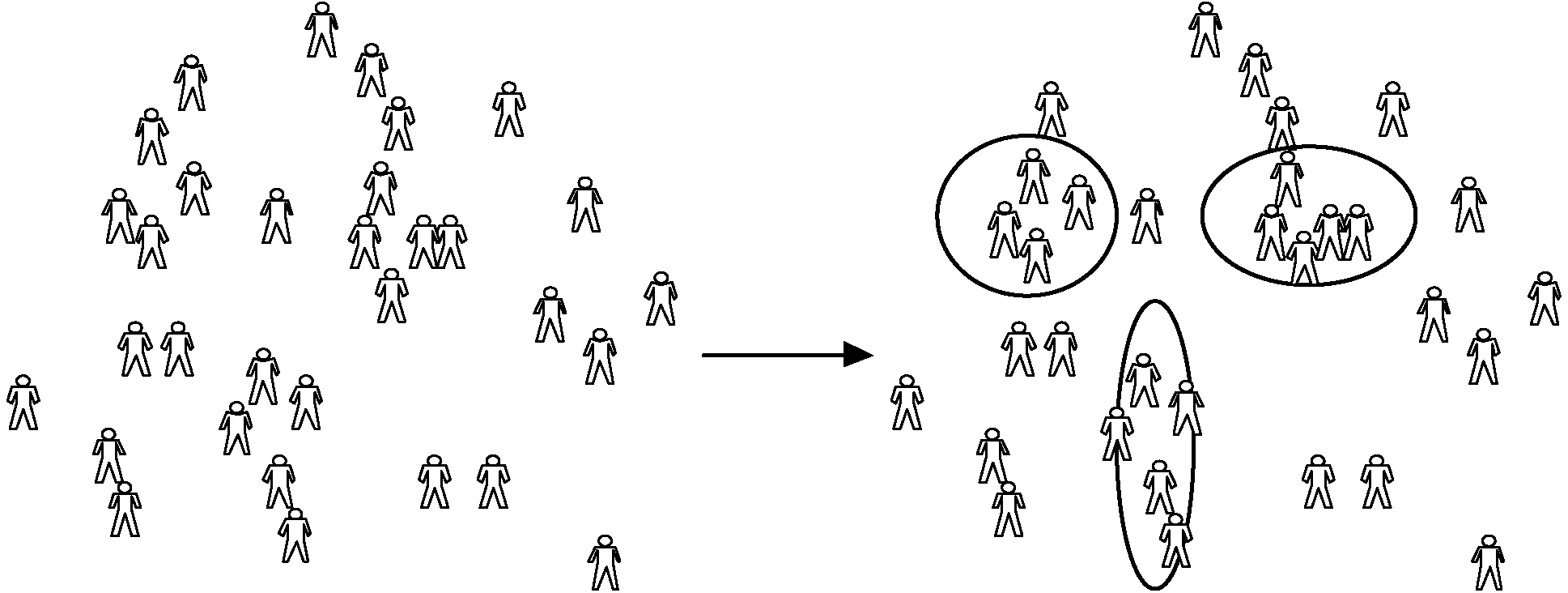
图3 群结构的形成

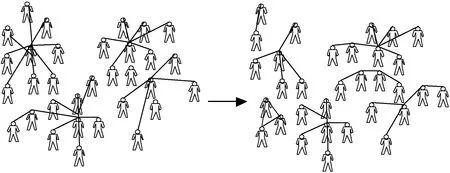
图4 节点边的断开

对于具有共同相邻结构的节点，我们可通过节点网络局部拓扑重合程度的量化，求其邻居集来说明节点受到的影响。

定义2在网络拓扑结构中节点两跳内所有邻居节点称为节点的邻居集。

若两个节点拥有共同的邻居结构，则节点受到相同的影响。节点A与节点B的共邻结构定义为节点存在共同的邻居集，其表达式如下：

(3)

式中：N(A)是指节点A的邻居集；N(A)∩N(B)表示节点A和节点B共有的邻居；N(A)∪N(B)表示节点A和节点B所有的邻居。当节点A与节点B存在多个相同的邻居时，则节点A与节点B共邻结构性越高，他们所受到的影响越相同。

对于群结构变化作于节点的影响定义为:

ifn(i)join one group

thenn(i)neighbors increase and group clustering increase

ifn(i)leave one group

thenn(i)weight change with neighbor

它表示群结构的形成促使节点边的建立和群聚类变化，群结构的变化促使节点边缘权重发生变化，n(i)表示节点i。

3 基于相似性的社交网络建模

综合第2节内容，本文从节点的内在属性与外在行为活动，以及网络结构背景影响来提出相似网络模型，在网络演化过程中节点A与节点B的节点相似度S为：

S(A,B)=activity(A,B)⊗neighbor(A,B)⊗

character(A,B)

(4)

式中：⊗算子表示在社交网络生长过程中由节点的内在属性与外在行为活动以及网络结构共同作用所产生的演化关系。节点A与节点B有边的关系的概率取决于两者某些属性相似的程度，相似度越高，节点A与节点B越有可能连接。

基于以上所考虑的签到集，节点特征，网络结构，本文提出了一种相似网络模型。在构建网络的过程中针对不同属性的新加入节点根据不同的相似性指标来进行网络的外部增长，并对网络中已有的节点进行内部演化，在此基础上不断更新网络中的边缘关系，直到网络规模达到预期。具体模型算法过程如下所述。

步骤1网络初始状态下，设置共有m0个节点，它们呈现随机连接的状态并赋予这m0个节点属性特征，同时设置一个规模上限N、相似度阈值T，以及一个节点度上限值θ。

步骤2网络中每新增一个节点，就赋予该节点属性特征，包括该节点的位置集群和个性特征。

步骤3根据式(1)-式(2)来计算所增节点与其他节点的行为相似与特征相似度。当行为相似与特征相似的加权和大于阈值相似度T时，建立新增节点与所属网络节点的边。该步骤实现了社交网络的外部增长。

步骤4已经存在于网络中的个体节点根据节点共邻结构和群结构来进行两两连接。节点会由于邻居拓扑结构和群结构的形成与其他节点建立边关系或断开边关系。当两个节点拥有多个共同的节点或两节点一起组成新的群结构时建立连接，当两个节点属性变化时不再存有共同的行为相似和特征相似，则断开边的连接关系，根据式(3)和群结构作用于节点影响的伪代码来完成。该步骤实现了社交网络的内部演化，即存在网络中的节点有新的边产生也有旧的边断开。

步骤5遍历网络中已生成的个体节点，判断其节点度是否大于θ。对于节点度大于θ的个体节点，它们将与节点相似性最小的邻居节点断连；对于节点度小于等于θ的个体节点，它们将随机与节点相似度低的一级邻居节点断连。根据邓巴数的概念，人类拥有稳定社交网络的人数，当社交网络中某个用户的节点度达到一定的上限值后，则认为该用户的节点度达到饱和，其必然要与某些弱连接的邻居移除边缘关系来为下一步的网络生长提供空间，而其他不饱和节点也会随机与某些弱连接的邻居进行断连。该步骤实现了社交网络边缘关系的更新。

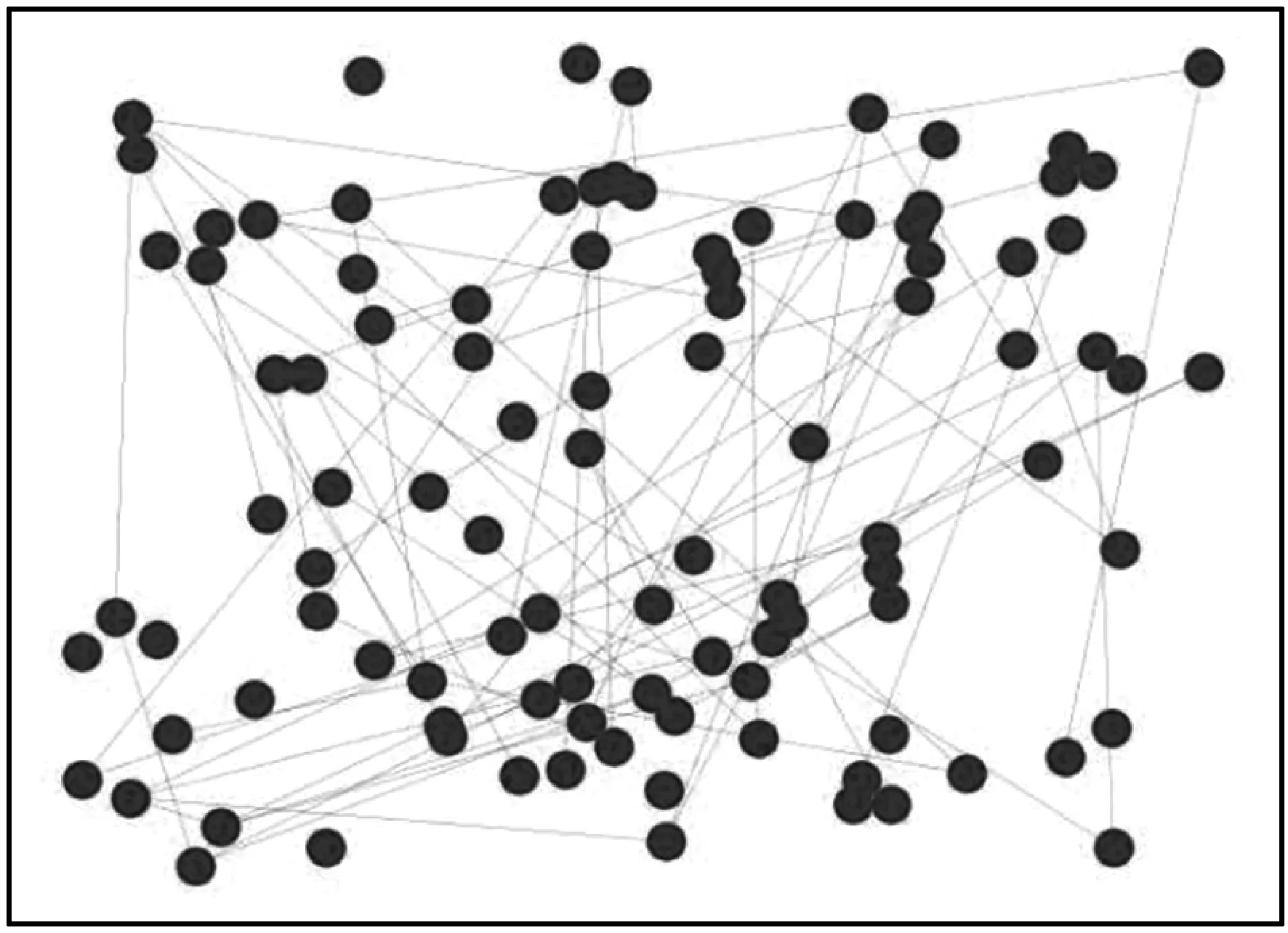
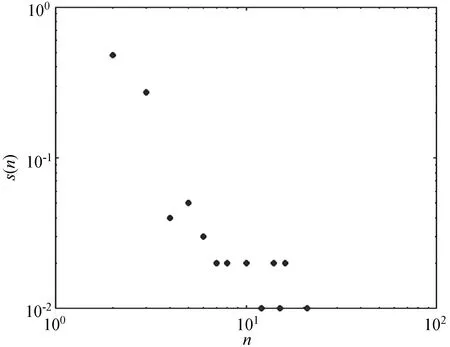
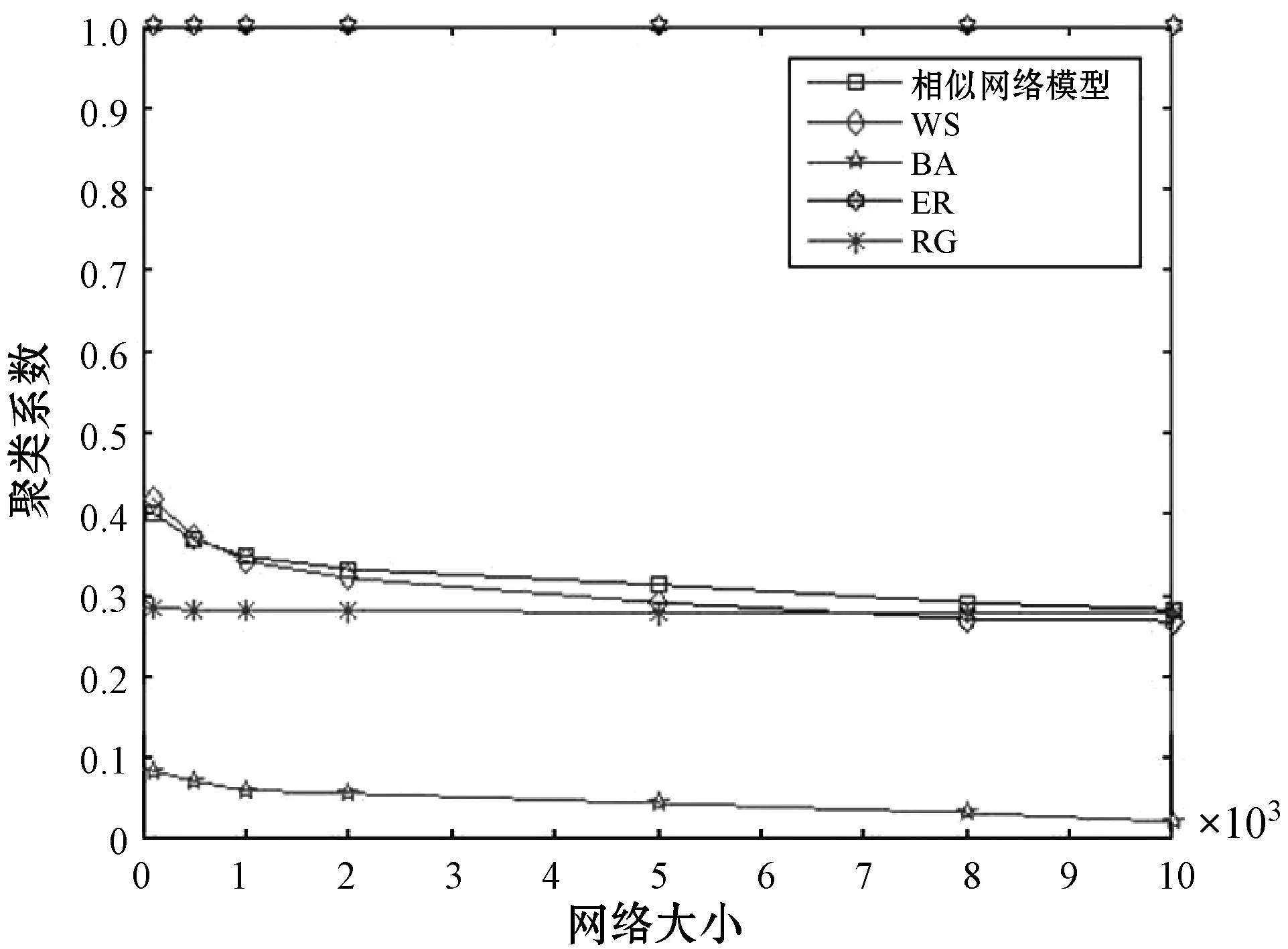
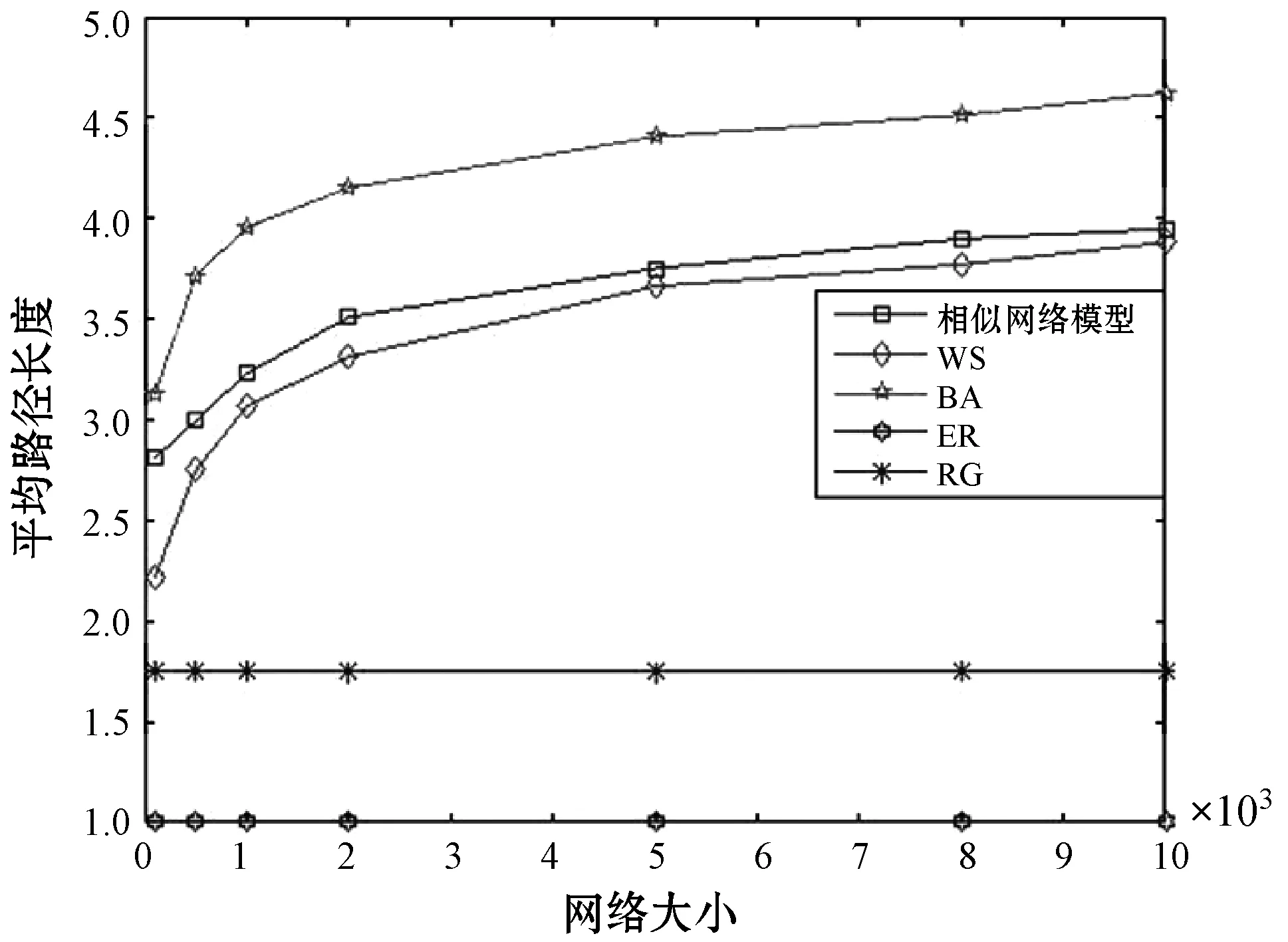
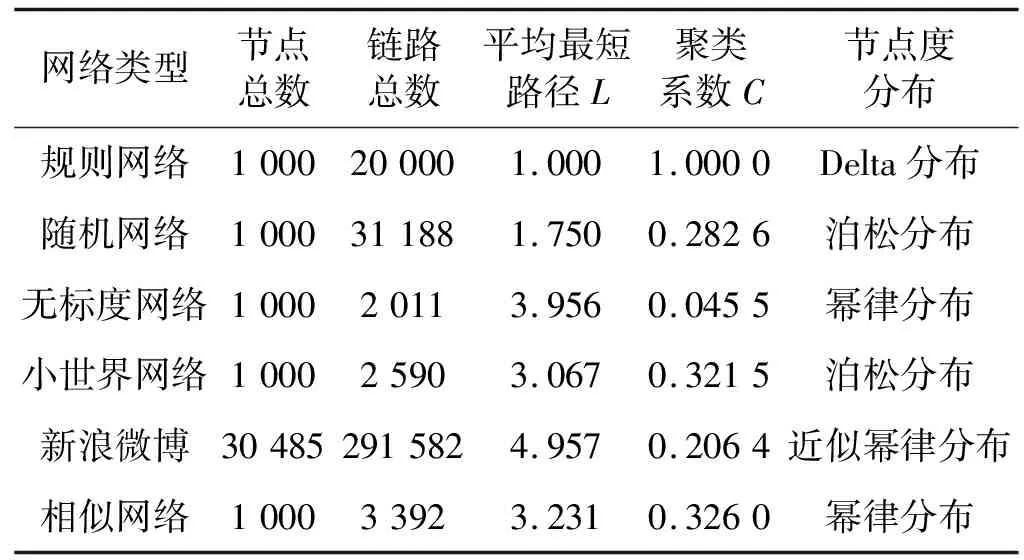
步骤6比较此时网络中个体节点数N0与网络规模上限N，当N0

与传统模型算法相比，该算法在基于相似性的社交网络演化生长的过程中，不仅考虑了节点的内在属性和节点的外在行为，而且考虑了网络结构的影响。网络中节点边缘关系的变化不只产生在新节点间，也存在于旧节点之间。节点间的边缘关系也不仅考虑了链路的建立，还考虑了链路的移除。社交网络的生命周期会经历增长、扩展、均衡、更新四个阶段。网络中节点与节点间关系的变化是不规律的，呈现出局部起伏变化，整体节点规模呈螺旋式上升。本文所提出的基于相似性的社交网络建模符合社交网络的增长模式与内部演化结构。

4 仿真与结果分析

本文实验使用Python语言，实验初始化节点设为m0=6；根据邓巴数的概念，每个节点的节点度上限设为θ=150；考虑到真实网络相似节点的连接，我们建立相似度阈值T=0.75。网络上限N∈{100,500,1 000,2 000,5 000，8 000,10 000}。

4.1 网络拓扑

网络构建效果如图5所示。N=100的网络是一个小型的社交网络，其边缘比较稀疏，节点的度值都比较小，存在少量孤立节点。N=1 000和N=5 000的网络是中等的社交网络，边缘相对密集，节点的度值相对较大，它能划分成多个结构相似的网络，也显现出了整体网络结构与部分网络结构相似性，即具有网络相似性。随着节点的不断增加，得到了N=10 000的大型社交网络，其边缘密集，许多节点度达到了邓巴数上限值150，具有一定的社团结构。节点的活动集群越多，就越容易与其他节点建立边的关系。整个演化过程，随着节点数的不断添加，边缘的密集性、节点度的变化呈现出网络结构相似性，这与实际的社交网络演化一致。

(a)N=100

4.2 度分布

在本文提出的相似网络中，度分布表示的是网络中一个节点所拥有的边的数量。图6展示了不同节点规模的社交网络所呈现的度分布。可以看出拥有不同节点规模的社交网络的度分布都近似呈现出幂律分布的特征，而且幂律指数变化区间为2～3。显然，这表明幂律并不总是优先联系的结果，并且随着网络规模的增大，节点度出现两极分化，在考虑边缘关系的更新与度饱和的状态下消除了网络中节点拥有巨大度的情况，这与实际社交网络特征一致。

(a)N=100

4.3 聚类系数与平均最短路径

本文将相似网络的聚类系数和平均路径长度与复杂网络基本网络模型进行了比较，其中：WS表示小世界网络；BA表示无标度网络；ER表示随机网络；RG表示规则网络。越来越多的节点加入使得网络规模增大，网络的聚集性被不断稀释，这使得网络的聚类系数不断减小。图7为聚类系数随网络大小增大的变化曲线，在相同的网络规模下，相似网络的聚类在[0.282,0.401]之间，BA的聚类在[0.021,0.088]之间，WS的聚类在[0.268,0.418]，ER与RG的聚类基本不变化，因此相似网络的聚类高于BA网络，低于WS网络，这符合实际社交网络聚类变化的特征。网络中新的链路的生成促使网络中的平均最短路径长度不断增大。从图8所示的平均路径长度变化曲线可知，相似网络的平均路径长度在[2.811,3.948]之间，而BA的平均路径长度在[3.128,4.612]之间，小世界的平均最短路径为[2.218,3.881]，ER与RG的平均最短路径基本不变化，这表明相似网络的平均路径长度小于BA，大于WS，这与实际社交网络最短路径变化一致。可见，基于相似性和网络结构影响形成的网络更容易聚集，平均路径长度更短，具有更快的信息传输，这些特征变化都符合实际社交网络特征的变化。

图7 聚类系数

图8 平均最短路径

表1直观地给出了复杂网络基本网络模型的统计特征对比，其中新浪微博的数据从微博数据中心获取。可以看出，现实生活中的社交网络同时拥有较短的平均最短路径和较大的聚类系数，度分布近似幂律分布。规则网络和随机网络的平均最短距离太小，与实际情况不符。小世界网络的度分布呈现泊松分布，也与实际情况不符。无标度网络的度分布很好地呈现了现实网络的特征，但其聚类系数较小，不符合实际情况。本文所提出的相似网络模型不仅度分布呈现幂律分布，还同时具有较短的平均最短路径和较大的聚类系数，可以较好地反映真实网络的情况。

表1 复杂网络基本网络模型的统计特征对比

5 结 语

社交网络结构建模与现实世界演化越一致，越有利于研究其他基于社交网络动态特征分析的内容。本文提出了一种相似网络模型。仿真结果显示，该模型的度分布近似呈现出幂律分布，所产生平均路径小于BA网络，聚类系数大于BA，其链路数随着网络规模的扩大在建立与阻断的过程中呈螺旋式增长，表明本文模型更接近社交网络结构特征。

未来工作可以考虑节点间特定的关系对社交网络的影响来构建社交网络模型。如互锁效应，当一个节点在网络中受到影响时，与其相关的其他节点在某种程度上也会受到影响，此时网络结构会有所波动，考虑更多符合实际网络的特征来构建模型能够达到更加逼近现实社交网络的效果。