拉格朗日微分中值定理纵横观
2020-12-12 09:35:06卢占化
卷宗 2020年28期
卢占化
(商丘工学院 基础部,河南 商丘 476000)
1 引言
拉格朗日定理:设函数f(x)在闭区间[a,b]上连续,在开区间[a,b]内可导,可设a<b则,则至少存在一点ξ∈(a,b),使得成立.
显然罗尔定理是拉格朗日定理的特殊情况,拉格朗日定理可以进一步推广为柯西中值定理.这些结论,可用于讨论泰勒展开式,洛必达法则等,它是微积分学的精华.学习及研究这部分内容,无论从理论上,还是从应用上都有重要意义.
2 若干结论
结论1 如果函数满足以下条件:
1)f(x)在闭区间[a,b]上连续;
2)f(x)在开区间(a,b)内可导.
那么,至少存在一点ξ∈(a,b)使得成立.
证明 反向分析法 作辅助函数

容易验证

即φ(a)=φ(b).应用罗尔定理,至少存在一点ξ∈(a,b),使得φ'(ξ)=0.
结论2 设函数f(x)满足的条件如结论1所述,则至少存在一点ξ∈(a,b),使得
证明 作辅助函数
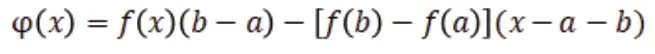
容易验证

即φ(a)=φ(b).应用罗尔定理,至少存在一点ξ∈(a,b),使得φ'(ξ)=0.
结论3 函数f(x)满足结论1的条件,则至少存在一点ξ∈(a,b),
使得

证明 作辅助函数

其中c为一个常数.容易验证
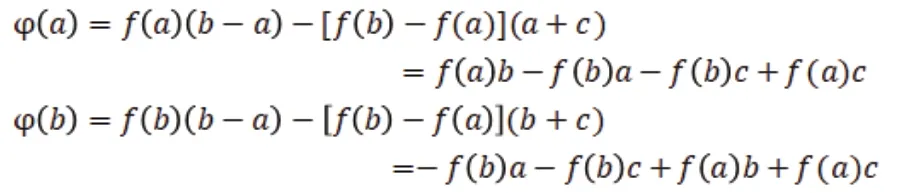
即φ(a)=φ(b).应用罗尔定理,存在ξ∈(a,b),使得φ'(ξ)=0.
3 几何意义
的关键是后面的式子k(x+c),k=f(b)-f(a).事实上这样的c有无穷多
例如 记k=f(b)-f(a),c=1,c=2,可以得到如下一些平行线.

由此可以看出这样的φ(x)有无穷多.它们通过某个函数可以上下平移得到.通过这些分析,便于启发学生探讨问题,开阔学生视野,提高学生学习兴趣.
猜你喜欢
科技风(2022年32期)2022-12-01 01:09:14
数学物理学报(2019年1期)2019-03-21 05:26:18
咸阳师范学院学报(2016年6期)2017-01-15 14:18:41
水利科技与经济(2016年9期)2016-04-22 01:07:30
智富时代(2015年9期)2016-01-14 06:51:24
佳木斯大学学报(自然科学版)(2015年5期)2015-04-14 08:06:10
科普童话·百科探秘(2014年7期)2014-08-07 01:41:31
太空探索(2014年3期)2014-07-10 14:59:39
武汉工程大学学报(2014年4期)2014-04-25 11:31:06
故事大王(2014年2期)2014-02-20 01:48:37

