基于传输相位和几何相位协同调控的消色差超透镜

申益佳，谢 鑫，蒲明博，张 飞，马晓亮,3，郭迎辉，李 雄，王长涛，罗先刚*

基于传输相位和几何相位协同调控的消色差超透镜

申益佳1,2，谢 鑫1,2，蒲明博1,2，张 飞1，马晓亮1,2,3，郭迎辉1,2，李 雄1,2，王长涛1,2，罗先刚1,2*

1中国科学院光电技术研究所微细加工光学技术国家重点实验室，四川 成都 610209；2中国科学院大学光电学院，北京 100049；3中国人民解放军军事科学院国防科技创新研究院，北京 100071

超透镜是超表面在成像领域中具有较大应用潜力的平面光学器件，但限于色差和较窄的工作带宽，通常难以应用于彩色成像及显示技术。本文设计了一种相位调控型透射式超透镜，实现了400 nm～650 nm波段的宽带消色差聚焦功能，带宽范围内焦平面处的平均聚焦效率约为29%。该方法利用具有低损耗、高折射率优势的二氧化钛(TiO2)介质柱结构，在可见光波段内获得了类似截断波导产生的传输相位响应。同时分析了几何相位和传输相位相结合的色散调控机制，并使用粒子群算法对构建的相位响应仿真数据库进行优化，完成了实际波面与理想聚焦波面的相位匹配。设计的宽带消色差器件有望在显微成像、计算机视觉和机器视觉等领域发挥作用。

超透镜；可见光；消色差；宽带

1 引 言

超表面能够在亚波长尺度内实现对光波的灵活调控，因而在平面光学领域具有广阔的发展前景[1-2]。目前，基于超表面的许多应用已经得到证实，例如光束发生器[3-8]、光学全息成像[9-12]、虚拟赋形[13-14]等。同时，超表面作为平面透镜可以通过产生一个双曲相位面，获得较大衍射效率的聚焦光束[15-18]。传统折射透镜通过改变光学材料的厚度来实现相位积累，通常为曲面构型，相比之下，超透镜则能够在平面内实现电磁波的相位调制，具有轻量化、易集成等优势。然而，受限于材料的固有属性超透镜往往存在较强的色差。

近年来，一些研究者通过对超透镜的单元结构进行优化设计可以实现特定离散波长或者一定光谱带宽的消色差成像[19-20]。2015年，Li[17]等人提出了一种使用结构色散和材料色散相互补偿的方法，克服了平板集成光学元件中存在的色差问题，实现了在1000 nm~2000 nm波段具有消色差功能的超表面透镜。2016年，哈佛大学Capasso[21]研究团队通过将两块超透镜级联在一起组成了双层超表面透镜，其工作波长为450 nm~700 nm，数值孔径为0.44，视场为50°。该级联透镜不仅可以实现倍率色差矫正，而且可以实现高质量成像。随后该团队利用低损耗、高深宽比的二氧化钛(TiO)纳米柱，并且在聚焦公式中引入一个仅与波长相关的优化因子()[22]，以及结合优化算法，从理论上和实验上实现了具有消色差功能的反射式超透镜，在490 nm~550 nm范围内其焦距保持不变。2018年，Chen等[23]利用多类纳米柱结构组成的超级单元，实现了对电磁波相位、群时延和群时延色散的同时控制，在可见光区域(470 nm~670 nm)获得了连续宽带消色差的效果。同时，Wang等[24]研究人员基于相同原理利用GaN纳米柱和纳米孔两类互补单元结构组成的超透镜实现了宽带消色差成像的功能。但是，此类方法往往需要对单元结构进行复杂多样的形貌设计，在一定程度上给超透镜的全模优化设计和加工制造过程带来较大难度。

本文设计了以二氧化硅(SiO2)为衬底的二氧化钛纳米柱单元结构，实现了对设计波段的透射相位调制。利用传输相位和几何相位复合的原理，并借助粒子群优化算法(particle swarm optimization, PSO)搜索最优的相位分布以及结构排布方式以消除轴向色差。最终设计的超透镜器件尺寸为21.6mm，数值孔径=0.263，在正入射的条件下将400 nm~650 nm的平面波汇聚到轴上的同一焦点，可保持焦距=38mm不变。

2 宽带消色差超透镜原理及单元结构设计

2.1 消色差原理

聚焦超透镜的相位分布如下[25]：

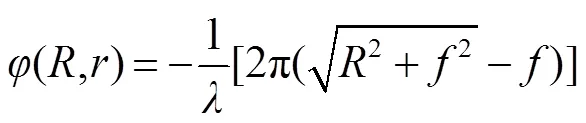
其中：

式(3)的相位差因此变为

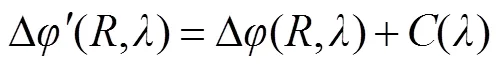
其中()是一个由优化算法得到的仅与波长相关的相位因子。

2.2 单元结构设计

为了满足消色差超透镜的相位要求，设计了一种基于波导模式的纳米介质柱单元结构，这些纳米柱结构可以周期性地排列和旋转，因此能够提供与它们的空间位置相对应的参考相位(几何相位)和相位补偿(传输相位)。如图2(a)，宽带消色差超透镜仅由二氧化钛纳米柱组成，可以通过改变纳米柱结构的占空比引起等效折射率的变化，从而调控透射光的传输相位分布[28]。如图2(b)所示，不同结构参数组合(，)会产生斜率不一样的相位-频率曲线(实线)，并且其左旋圆偏振(LCP)光转化为右旋(RCP)的偏振转化效率高于40%(虚线)。

图2(c)表明诱发的光场高度集中在介质柱结构内部，因此与相邻结构的相互作用几乎可以忽略不计。除了改变几何参数外，还可以激发更高阶的波导谐振以获得较大的相位补偿，这可以通过直接增加纳米柱的高度来实现。为了尽量抑制高阶衍射级次带来的能量损失，通常设置单元结构的周期小于自由空间传输的最小波长。如图2(a)所示，设计的正六边形单元结构边长为120 nm，采用基底为SiO2，上层为高600 nm的TiO2纳米柱。由于单元结构的正六边形排布方式具有足够的旋转对称性，因此能尽量确保纳米柱旋转过程中的偏振敏感特性以及透过率的均匀分布。目前通常利用电子束直写与原子层沉积相结合的方法来制备高深宽比的TiO2纳米柱阵列透镜[29-30]。然后需要使用CST(computer simulation technology)仿真软件对单元结构的几何参数进行扫描，获得不同几何参数单元结构的传输相位及偏振转化效率，其中参数扫描的范围为50 nm<<180 nm和45 nm<<140 nm。然后利用这些相位、振幅等数据，建立全模设计工作中所需要的数据库。

图2 单元结构仿真结果。(a) 宽带消色差超透镜的单元结构示意图；(b) 偏振转换效率(虚线)和相位响应曲线(实线)，其不同结构参数组合(l: 71 nm, w: 125 nm、l: 162 nm, w: 105 nm、l: 176 nm, w: 125 nm)相位响应曲线斜率是变化的；(c) 在不同入射波长下，结构参数为l=105 nm，w=80 nm时归一化磁场能量分布，其中黑色线表示TiO2结构的边界

3 设计方案

3.1 粒子群优化算法

在2.1节中讨论到，对于每个波长的理想相位分布由式(1)给出。但实际上超透镜所给出的实际相位波面并不能与之完美地匹配，它们之间的差异通过引入一个()转化为一个求其极小值的数学问题。对于极值的求解方法复杂多样，随着计算机技术普及和其强大的计算能力，人们提出了多种智能优化算法(如遗传算法、模拟退火算法、蚁群算法等)，本文选取了其中实现方式简单和全局搜索能力强的粒子群优化算法(PSO)来搜索计算波像差的极小值。

1995年，Kennedy和Eberhart[31]受到鸟群觅食行为的启发，并对其进行深入研究和探索进而提出了一种强大的粒子群优化方法。在PSO算法中，每个粒子可以使用三维向量构成，包括当前位置，之前的最佳位置和飞行速度。为了实现粒子群的优化过程，整个优化迭代过程中粒子速度和位置的变化可以表示：

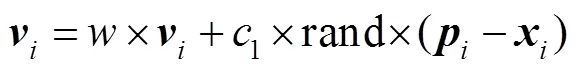
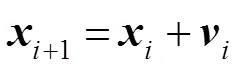
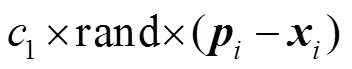
3.2 实施方案

根据图2(a)中所设计的亚波长单元结构，除了基础参数和固定不变之外，其它尺寸参数、都在CST仿真软件中作为变量进行扫描，产生优化过程所需要的结构参数-相位响应和结构参数-振幅响应等数据库。初始化过程之前，需要对数据库重新处理并构建结构编号－结构参数－相位响应－振幅响应一一对应的参数矩阵，便于调用。

当考虑不同波长的光波入射时，其总的波像差可以表示如下：

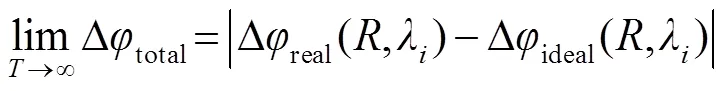
其中：是迭代次数，real表示从数据库中随机取出数据生成的实际波面，∆ideal代表由式(4)计算得到的理想波面，而∆total则表示针对每个位置处每个波长波像差的总和。整个优化过程如图3(a)所示，主要思想就是通过迭代不断地缩小波像差，并尽可能地利用相位数据库当中的数据实现理想波面与实际波面的相位匹配，当满足瑞利判据时循环停止。瑞利判据认为：当实际波面和理想波面之间的最大波像差不超过/4时，该波面可认为是没有缺陷的。并且还指出，缺陷部分在整个波面面积如果所占比重较小，即使波像差大于/4，这些局部缺陷仍旧可以忽略[32]。因此本文可以将迭代次数初步设定为500。图3(b)显示随着迭代次数的增加总的波像差不断减小，当循环到500代时其曲线逐渐收敛，同时考虑到计算时间和数据量，不可能无限制地增大迭代次数，况且此时优化的全模结构已经可以满足设计目标。这里引入的相位因子()可以将一个寻找单元结构几何参数的抽象问题，转化为一个求∆total极小值的数学问题。本文的电脑配置为Windows 10操作系统，CPU Intel(R) Core(TM) i7-8750H@2.2 GHz，GPU NVIDIA GeForce GTX 1050Ti，RAM 8 G，整个优化时长约为6.4 h。全模结构尺寸大小为20.8mm´21.6mm矩形超透镜，该超透镜由120´100个优化设计的单元结构构成。其水平径向边缘位置到中心的60组结构参数如图4所示，全模设计采用六边形排布方式使得单元结构相互交错排列，图中相邻单元结构之间的位置差所对应的实际物理尺寸为3/2。

4 可见光的宽带消色差超透镜的仿真结果

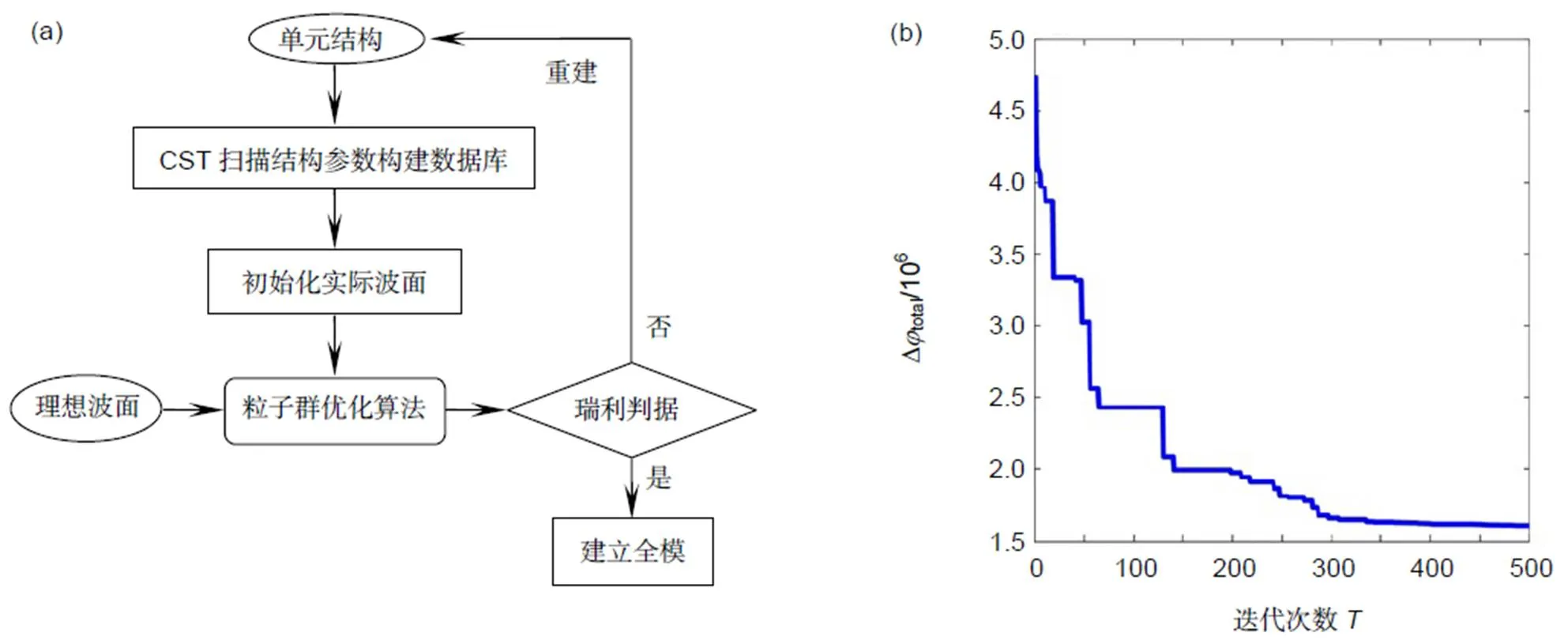
图3 (a) 宽带消色差超透镜的粒子群优化流程图；(b) PSO收敛曲线

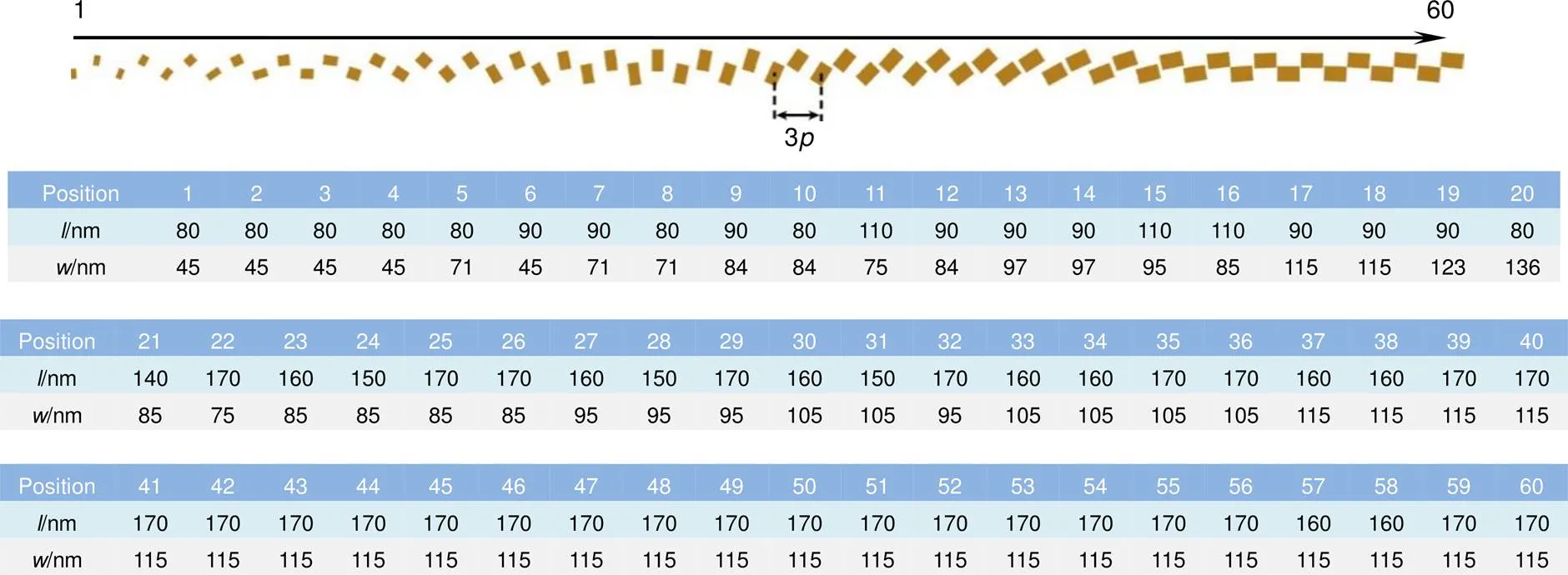
图4 超透镜径向单元结构对应的结构参数

利用该方案，设计并实现了数值孔径为=0.263、物理尺寸为20.8mm´21.6 μm和焦距=38 μm的宽带消色差超透镜。首先，使用粒子群优化算法对所需的参考相位和相位补偿进行数字化设计；然后，将这些相位从扫描得到的数据库中筛选出来，如此尽可能地利用该数据库中的相位响应数据；最后，根据具体PSO优化算法得到的结构参数建立消色差超透镜模型，并使用专业仿真软件CST进行全模仿真验证。全模的仿真计算往往需要大量计算时间和数据量，同时仿真区域的变大也会限制计算速度。因此，本文先利用CST计算近场光场分布，然后利用矢量角谱理论计算其传播过程，从而获得焦平面处的远场光强度分布。

图5(a)得到了可见光范围(400 nm~650 nm)内左旋圆偏振光正入射条件下的光场分布。其中，上部分为平面的归一化强度分布，下部分表示平面内的聚焦光斑效果图。白色实线是理论焦距=38mm，同时黄色虚线表示焦平面处的点扩散函数。正如预测的那样，当入射波长在整个可见光谱范围内变化时，所有焦距几乎保持不变，焦距最小值和最大值分别为36mm，40mm，与设计的焦距38mm相差在2mm以内(相对误差为5.2%)。此外，图5(a)清晰地展示了焦点具有一定的焦深5mm，因此这样的误差几乎可以忽略。图5(b)显示了该透镜焦距作为入射波长的变化曲线，同样表明了焦距在理论值附近仅有一些细微的波动。同时，对400 nm~650 nm内的光波长离散取值(408 nm，444 nm，487 nm，512 nm，570 nm，605 nm，644 nm)，并获得了图5(c)中的消色差超透镜的聚焦效率(用黑色曲线表示)和半高全宽(用红色曲线表示)。其中，聚焦效率为一个艾里斑内聚焦圆偏振光束的光强度与透射光束的光强度之比。图5(c)显示了聚焦效率曲线随工作波长的变化而变化，其中最高效率可达43%，平均效率在整个工作带宽内约为29%，而这种变化主要是由谐振单元结构的偏振转换效率波动引起的。为了获得更高的偏振转化效率，可以在粒子群优化过程中淘汰偏振转化透过率过低的参数组合，亦可直接优化单元结构的几何参数(和)以达到聚焦效率较为均匀的目的。图中模拟七个焦点的理论衍射极限FWHM值分别为0.78mm，0.85mm，0.93mm，0.97mm，1.08mm，1.15mm和1.23mm，仿真得到的FWHM值为0.8mm，0.95mm，1.2mm，1.25mm，1.22mm，1.25mm和1.26mm，计算结果与理论衍射极限具有较好的一致性。

5 总 结

本文设计了一种宽带消色差超表面器件，利用几何相位和传输相位复合的调控原理，结合周期性排列的谐振单元结构，实现了对可见光波段的色散调控。设计的单元结构由六边形SiO2衬底和TiO2介质柱组成，并使用CST商业仿真软件对单元结构的几何参数进行扫描，建立纳米柱几何参数与相位、振幅响应的数据库。同时，引入相位优化因子()进行相位补偿，最后借助粒子群优化算法完成对超透镜全模的优化设计，在400 nm~650 nm波段实现了消色差聚焦功能，平均聚焦效率约为29%。本文提出的宽带消色差平面光学器件采用的单元结构设计简单，可以引入更多类型的谐振单元实现更大带宽的消色差聚焦效果，在彩色显示成像系统等领域存在一定的应用前景。虽然本文只在可见光区域进行了仿真验证，但该器件的设计原理和方法可以推广到红外等其它波段。

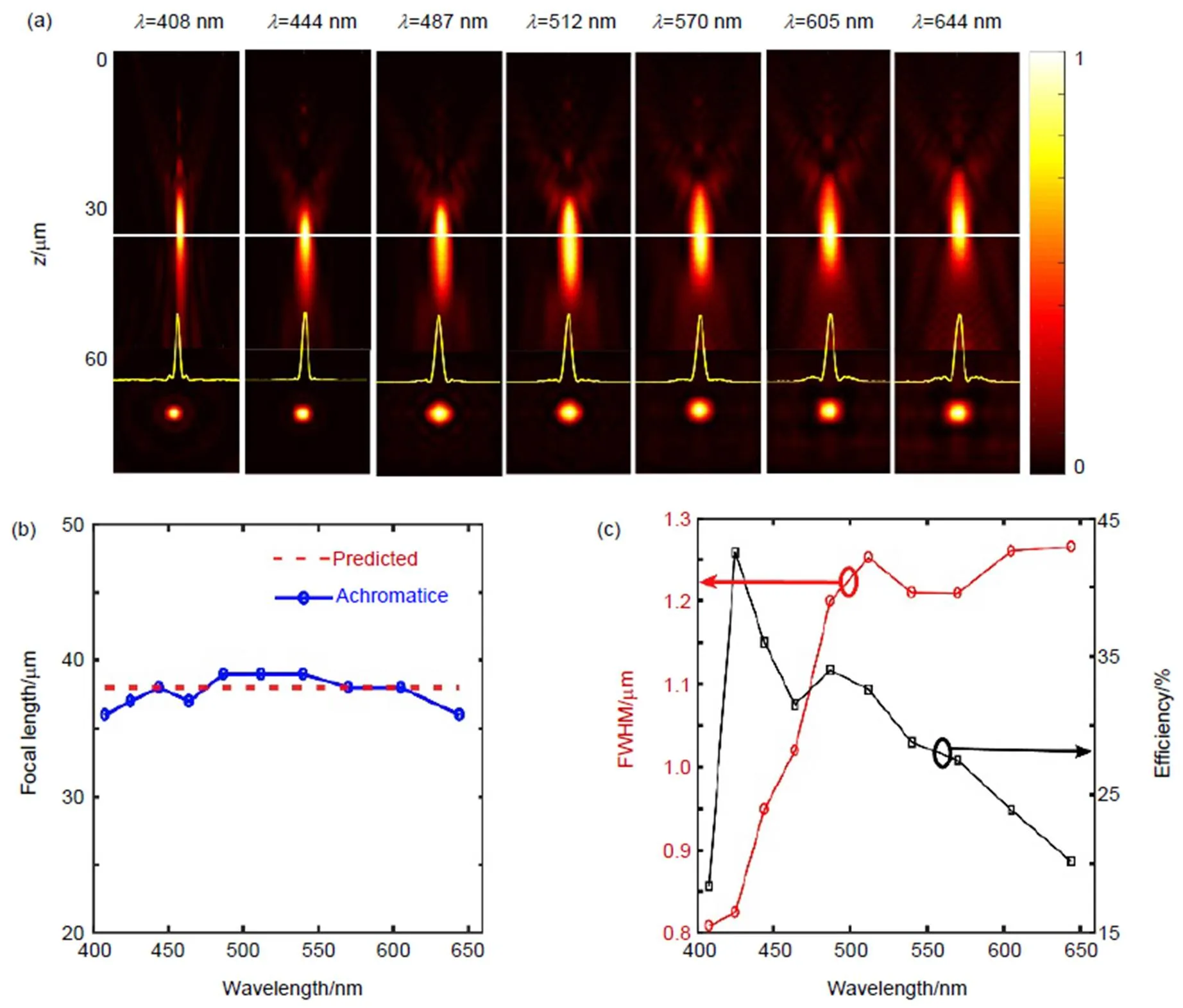
图5 超透镜的焦距偏移和强度分布的模拟结果。(a) 在正入射的条件下，y-z平面的归一化仿真强度分布及其x-y平面内的聚焦光斑效果图。入射方向是正z轴，白色实线表示理论焦距f=38 mm，黄色虚线代表点扩散函数；(b) 不同波长下模拟的焦距和理论预测焦距；(c) 聚焦效率(黑色曲线)和半高全宽(full-widths at half maximums，FWHM)(红色曲线)随着入射超透镜的波长变化

[1] Luo X G. Principles of electromagnetic waves in metasurfaces[J]., 2015, 58(9): 594201.

[2] Pu M B, Wang C T, Wang Y Q,. Subwavelength electromagnetics below the diffraction limit[J].2017, 66(14): 144101.

蒲明博, 王长涛, 王彦钦, 等. 衍射极限尺度下的亚波长电磁学[J]. 物理学报2017, 66(14): 144101.

[3] Wu P C, Zhu W M, Shen Z X,Broadband wide-angle multifunctional polarization converter via liquid-metal-based metasurface[J].2017, 5(7): 1600938.

[4] Pu M B, Li X, Ma X L,Catenary optics for achromatic generation of perfect optical angular momentum[J].2015, 1(9): e1500396.

[5] Yue F Y, Wen D D, Xin J T,Vector vortex beam generation with a single plasmonic metasurface[J].2016, 3(9): 1558–1563.

[6] Wang S C, Ouyang X Y, Feng Z W,. Diffractive photonic applications mediated by laser reduced graphene oxides[J]., 2018, 1(2): 170002.

[7] Li Z, Cheng H, Liu Z C,. Plasmonic airy beam generation by both phase and amplitude modulation with metasurfaces[J].2016, 4(8): 1230–1235.

[8] Chen J Y, Zhang F, Zhang M,Radially polarized bessel lens based on all-dielectric metasurface[J]., 2018, 45(11): 180124.

陈俊妍, 张飞, 张明, 等.基于介质超表面的径向偏振贝塞尔透镜[J]. 光电工程2018, 45(11): 180124.

[9] Huang L L, Mühlenbernd H, Li X W,Broadband hybrid holographic multiplexing with geometric metasurfaces[J].2015, 27(41): 6444–6449.

[10] Huang Y W, Chen W T, Tsai W Y,Aluminum plasmonic multicolor meta-hologram[J].2015, 15(5): 3122–3127.

[11] Ni X J, Kildishev A V, Shalaev V M. Metasurface holograms for visible light[J].2013, 4(1): 2807.

[12] Wan W W, Gao J, Yang X D. Full-color plasmonic metasurface holograms[J].2016, 10(12): 10671–10680.

[13] Ni X J, Wong Z J, Mrejen M,. An ultrathin invisibility skin cloak for visible light[J]., 2015, 349(6254): 1310–1314.

[14] Xie X, Pu M B, Li X,. Dual-band and ultra-broadband photonic spin-orbit interaction for electromagnetic shaping based on single-layer silicon metasurfaces[J]., 2019, 7(5): 586–593.

[15] Dou K H, Xin X, Pu M B,Off-axis multi-wavelength dispersion controlling metalens for multi-color imaging[J].2020, 3(4): 190005.

[16] Shrestha S, Overvig A C, Lu M,. Broadband achromatic dielectric metalenses[J].2018, 7: 85.

[17] Li Y, Li X, Pu M BAchromatic flat optical components via compensation between structure and material dispersions[J].2016, 6(1): 19885.

[18] Yan C, Li X, Pu M BMidinfrared real-time polarization imaging with all-dielectric metasurfaces[J].2019, 114(16): 161904.

[19] Khorasaninejad M, Aieta F, Kanhaiya P,Achromatic metasurface lens at telecommunication wavelengths[J].2015, 15(8): 5358–5362.

[20] Shi Z J, Khorasaninejad M, Huang Y W,Single-layer metasurface with controllable multiwavelength functions[J].2018, 18(4): 2420–2427.

[21] Groever B, Chen W T, Capasso F. Meta-lens doublet in the visible region[J].2017, 17(8): 4902–4907.

[22] Khorasaninejad M, Shi Z, Zhu A Y,Achromatic metalens over 60 nm bandwidth in the visible and metalens with reverse chromatic dispersion[J].2017, 17(3): 1819–1824.

[23] Chen W T, Zhu A Y, Sanjeev V,A broadband achromatic metalens for focusing and imaging in the visible[J].2018, 13(3): 220–226.

[24] Wang S M, Wu P C, Su V C,A broadband achromatic metalens in the visible[J].2018, 13(3): 227–232.

[25] Wang S M, Wu P C, Su V C,Broadband achromatic optical metasurface devices[J].2017, 8(1): 187.

[26] Pancharatnam S. Generalized theory of interference and its applications[J].1956, 44(6): 398–417.

[27] Berry M V. Quantal phase factors accompanying adiabatic changes[J].1984, 392(1802): 45–57.

[28] Zhang F, Pu M B, Li X,All-dielectric metasurfaces for simultaneous giant circular asymmetric transmission and wavefront shaping based on asymmetric photonic spin–orbit Interactions[J].2017, 27(47): 1704295.

[29] Devlin R C, Khorasaninejad M, Chen W T,. High efficiency dielectric metasurfaces at visible wavelengths[Z]. arXiv 1603.02735[physics.optics], 2016.

[30] Khorasaninejad M, Chen W T, Devlin R C,. Planar Lenses at Visible Wavelengths[Z]. arXiv 1605.02248[physics.optics], 2016.

[31] Kennedy J, Eberhart R. Particle swarm optimization[C]//, Perth, 1995, 4: 1942–1948.

[32] Barakat R. Rayleigh wavefront criterion[J].1965, 55(5): 572–573.

Achromatic metalens based on coordinative modulation of propagation phase and geometric phase

Shen Yijia1,2, Xie Xin1,2, Pu Mingbo1,2, Zhang Fei1, Ma Xiaoliang1,2,3, Guo Yinghui1,2,Li Xiong1,2, Wang Changtao1,2, Luo Xiangang1,2*

11State Key Laboratory of Optical Technologies on Nano-Fabrication and Micro-Engineering,Institute of Optics and Electronics, Chinese Academy of Sciences, Chengdu, Sichuan 610209, China;2School of Optoelectronics, Chinese Academy of Sciences, Beijing 100049, China;3National Institute of Defense Technology Innovation, Academy of Military Sciences PLA China, Beijing 100071, China

A broadband achromatic metalens in visible

Overview:As a two-dimension artificial electromagnetic material, metasurface provides the means to accurately control the wavefront by flexibly adjusting the phase, amplitude, and polarization of electromagnetic waves at will. At present, many applications based on metasurface have been proved, such as beam generator, optical holographic imaging, virtual shaping, and so on. As a plane lens, the metasurface can also generate a hyperbolic phase profile to obtain a focused beam with a higher diffraction efficiency. Traditional refractive lenses achieve phase accumulation by changing the thickness of optical materials, which is usually curved. In contrast, the metalens can realize phase modulation of electromagnetic waves in a plane manner. However, it is usually difficult to realize full-color imaging and display due to the narrow working bandwidth and large chromatic aberration which are caused by the intrinsic properties of the material. In this paper, a phase-controlled transmissive metalens is designed, to realize the broadband achromatic focusing within 400 nm~650 nm, and the average focusing efficiency is about 29% at the focal plane within the bandwidth range. The metalens is composed of titanium dioxide (TiO2) dielectric nanopillars arranged periodically on a silicon dioxide (SiO2,=1.45) substrate. The nanopillar possesses low loss and high refractive index which can be treated as a truncated waveguide to control the propagation phase in the visible. At the same time, we analyze the dispersion modulation mechanism which merges the geometric and propagation phases, and the particle swarm optimization (PSO) algorithm is used to optimize the phase response database, and accomplish the phase matching between the ideal focusing and the actual wavefronts and realize the designed function. The proposed broadband achromatic planar optical device has a simple structure design of unit cell, therefore we can introduce more types of resonance units to realize the achromatic focusing function with a larger bandwidth.

Citation: Shen Y J, Xie X, Pu M B,. Achromatic metalens based on coordinative modulation of propagation phase and geometric phase[J]., 2020,47(10): 200237

Achromatic metalens based on coordinative modulation of propagation phase and geometric phase

Shen Yijia1,2, Xie Xin1,2, Pu Mingbo1,2, Zhang Fei1, Ma Xiaoliang1,2,3, Guo Yinghui1,2,Li Xiong1,2, Wang Changtao1,2, Luo Xiangang1,2*

1State Key Laboratory of Optical Technologies on Nano-Fabrication and Micro-Engineering, Institute of Optics and Electronics, Chinese Academy of Sciences, Chengdu, Sichuan 610209, China;2School of Optoelectronics, Chinese Academy of Sciences, Beijing 100049, China;3National Institute of Defense Technology Innovation, Academy of Military Sciences PLA China, Beijing 100071, China

Metalens is considered as one of the most promising planar optical devices composed of the metasurface, but it is usually difficult to realize full-color imaging and display due to the narrow working bandwidth and large chromatic aberration. In this paper, a phase-controlled transmissive metalens is designed to realize the broadband achromatic focusing within 400 nm~650 nm, and the average focusing efficiency is about 29% at the focal plane within the bandwidth range. The titanium dioxide (TiO2) dielectric nanopillar with low loss and high refractive index as a truncated waveguide can control the propagation phase in the visible. At the same time, we analyze the dispersion modulation mechanism which merges the geometric and propagation phases, and the particle swarm optimization (PSO) algorithm is used to optimize the phase response database, and accomplish the phase matching between the ideal and actual wavefronts. The proposed broadband achromatic devices may broaden the applications of metalens in micro-imaging, computer vision, and machine vision.

metalens; visible; achromatic; broadband

TH74

A

申益佳，谢鑫，蒲明博，等. 基于传输相位和几何相位协同调控的消色差超透镜[J]. 光电工程，2020，47(10): 200237

10.12086/oee.2020.200237

: Shen Y J, Xie X, Pu M B,Achromatic metalens based on coordinative modulation of propagation phase and geometric phase[J]., 2020, 47(10): 200237

2020-06-26；

2020-07-29

国家自然科学基金资助项目(61822511，61675208)

申益佳(1994-)，男，硕士，主要从事微纳光学方面的研究。E-mail：15185286358@163.com

罗先刚(1970-)，男，博士，研究员，主要从事平面光学，微纳光学，微细加工等方面的研究。E-mail：lxg@ioe.ac.cn

Supported by National Natural Science Foundation of China (61822511, 61675208)

* E-mail: lxg@ioe.ac.cn