宏/子脉冲编码光子计数激光雷达
刘 博,姜 朔,于 洋,陈 臻
宏/子脉冲编码光子计数激光雷达
刘 博1,2,3*,姜 朔1,2,3,于 洋4,陈 臻1,2
1中国科学院空间光电精密测量技术重点实验室,四川 成都 610209;2中国科学院光电技术研究所,四川 成都 610209;3中国科学院大学,北京 100049;4齐鲁工业大学(山东省科学院),山东省科学院海洋仪器仪表研究所,山东 青岛 266001
光子计数激光雷达因其极高的探测灵敏度在远距离目标探测领域有着非常重要的作用。针对远距离、高速度的目标,普通的光子计数激光雷达无法简单通过统计直方图获得有用的回波信息。为了解决这一问题,本文提出了一种基于宏/子脉冲编码的光子计数激光雷达,利用时移脉冲累加的方法提取子脉冲的飞行时间进而在一个宏脉冲内获得目标距离信息。建立了宏/子脉冲编码光子计数激光雷达的理论模型,对虚警概率和探测概率的影响进行了分析,并通过蒙特卡洛仿真和实验验证了其对远距离高速径向运动目标探测的有效性。
宏/子脉冲;激光雷达;光子计数;目标探测
1 引 言
光子计数激光雷达具有对单光子敏感的高灵敏度,且能够提供非常精确的光子到达时间,因而被认为是一种很有前途的远距离探测方法[1-5],在空间碎片的探测与识别、星载地形测绘、交会对接、自动驾驶等领域受到研究学者的广泛关注[6-9]。这些空间探测领域有两个明显的特点:激光雷达平台与目标之间距离较远,一般为几十公里甚至几百公里;激光雷达平台与目标之间存在高速相对运动,如空间碎片或在轨航天器等,因此本文重点关注对高速相对径向运动目标的探测。在这些领域中,为了捕获快速运动的目标就要求激光雷达具有超远距离的快速探测能力。
与线性探测模式激光雷达相比,光子计数激光雷达使用统计采样技术,它需要积累足够的光子事件来建立统计直方图,通过建立的统计直方图来提取回波信息。而建立统计直方图就需要多次探测的脉冲累积,累积过程会极大地降低系统的测量速度,这也是光子计数激光雷达的主要缺点,尤其是当激光雷达系统和目标之间存在高速相对运动时更为突出。由于目标或激光雷达平台的相对运动,使得多个周期的激光脉冲回波之间具有不同的飞行时间间隔,多周期回波信号在时域难以体现聚类特性,因而给回波信息的提取带来了极大的难度。解决这一问题的有效方法就是尽量缩短激光雷达的测量时间,当测量时间短到可以忽略两者直接的相对运动时,通过回波信息具有的时域聚类特点仍然可以提取目标信号。
有研究人员提出使用高重复频率(几十MHz)的激光光源来减小数据的采集时间[10],然而高的脉冲重复频率会极大地减小系统的最大不模糊距离。对于传统的脉冲累加方法,长的不模糊距离与短的采集时间之间具有不可调和的矛盾,通过传统的脉冲累计方法难以实现远距离、高速运动目标的探测。Du[11]和Liang[12]提出了采用多个高脉冲重复频率的方法提高系统不模糊距离,能够较好地解决距离模糊问题,但对于高重频的激光脉冲,其峰值功率受限,无法实现远距离探测。
为了缩短测量时间,借鉴扩频通信的思想[13-14],基于伪随机编码的测距方法被提出。1983年,Takeuchi等[15]首次将随机相位编码方法用于激光雷达,提高了系统的信噪比。Hiskett[16],Krichel[17]和Ullrich[18]使用有限非周期脉冲串或者脉冲位置调制技术解决距离模糊问题。Zhang[19]采用伪随机编码光子计数激光雷达实现了1.2 km处的非合作目标成像。Yang[20]使用高速伪随机光纤测距系统实现了厘米级的高空间分辨率探测。然而,在伪随机编码方法中,通常使用激光二极管产生高频脉冲序列,这种方法同样难以获得高峰值功率的脉冲激光,因而也不适合远距离空间领域的探测。
为解决该问题,本文提出采用宏/子脉冲编码光子计数(macro/sub-pulse coded photon counting, MSCPC)激光雷达实现远距离高速运动目标探测。宏/子脉冲方法的最大不模糊距离由宏脉冲的周期决定,而测量时间由周期内所有子脉冲的总时间确定。一个周期内宏脉冲总的子脉冲间隔远小于相同脉冲个数的脉冲累计方法的总间隔,因而与传统脉冲累计方法相比,宏/子脉冲方法可以在一个宏脉冲实现探测,大幅缩短了探测时间,提高了最大不模糊距离。与伪随机编码方法不同,宏/子脉冲方法可以周期性地发射宏/子脉冲串,在相同的激光平均发射功率下可以得到更高的子脉冲峰值功率,因而能够实现更远距离的探测。因此,宏/子脉冲编码光子计数激光雷达可以有效地解决远距离、高速运动目标的探测。
2 系统描述
2.1 宏/子脉冲编码光子计数激光雷达系统结构
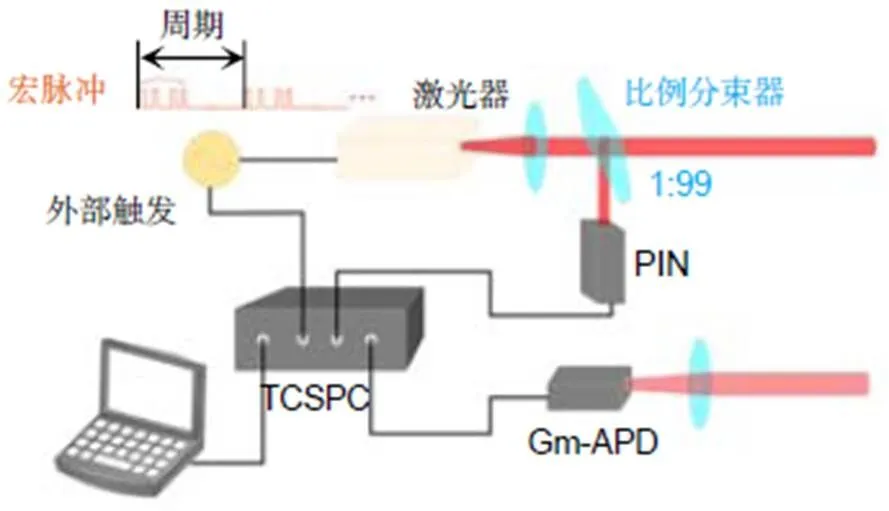
如图1所示,激光器发射的周期性的脉冲串被称为宏/子脉冲,例如图中将重频为1 kHz的等间隔激光脉冲编码为宏/子脉冲串,其中宏脉冲由8个子脉冲组成,宏脉冲重频为125 Hz(间隔8 ms),子脉冲重频为8 kHz(间隔0.125 ms),子脉冲的能量相同,激光发射平均功率相同。系统通过一个外部触发源同步。输出的宏脉冲通过比例分束器分成两个部分:其中能量较小的部分由PIN探测,被用作发射参考信号;能量较大的部分用来探测目标。被目标散射的回波信号通过光学系统接收、并由Gm-APD (Geiger-mode avalanche photodiode)完成探测。需要指出的是,在宏/子脉冲激光雷达系统中,任意两个子脉冲具有不等的脉冲间隔,这一特点可以有效地避免距离模糊。
2.2 宏/子脉冲编码光子计数激光雷达系统测距原理
针对宏/子脉冲光子计数激光雷达,本文提出了时移脉冲累加的飞行时间提取方法。在时移脉冲累加方法中对接收信号没有特殊的要求,但是需要事先知道发射信号的子脉冲间隔。为了满足这一要求,系统采用PIN 探测器对发射序列进行实时记录。基于此子脉冲之间的时间间隔被测量并保存,作为系统已知参数。如图2所示,在一个周期内,由Gm-APD(Geiger-mode avalanche photodiode)探测器探测的回波信号按照子脉冲间隔顺序移位,将顺序移位后的回波信号进行累加。图2中的红色点线表示发射的子脉冲没有被探测,黑色虚线表示时移脉冲累加方法中由于时间延迟补偿而产生的无效数据。累加后峰值的位置(红色实线)对应于宏脉冲的飞行时间。换言之,由于每个子脉冲相对于第一个子脉冲的延迟时间是已知的,因此宏脉冲的飞行时间等于子脉冲在其延迟时间被补偿后的飞行时间。将延迟时间补偿后的子脉冲进行脉冲累加,可以有效地提高信噪比,有利于宏脉冲飞行时间的提取。
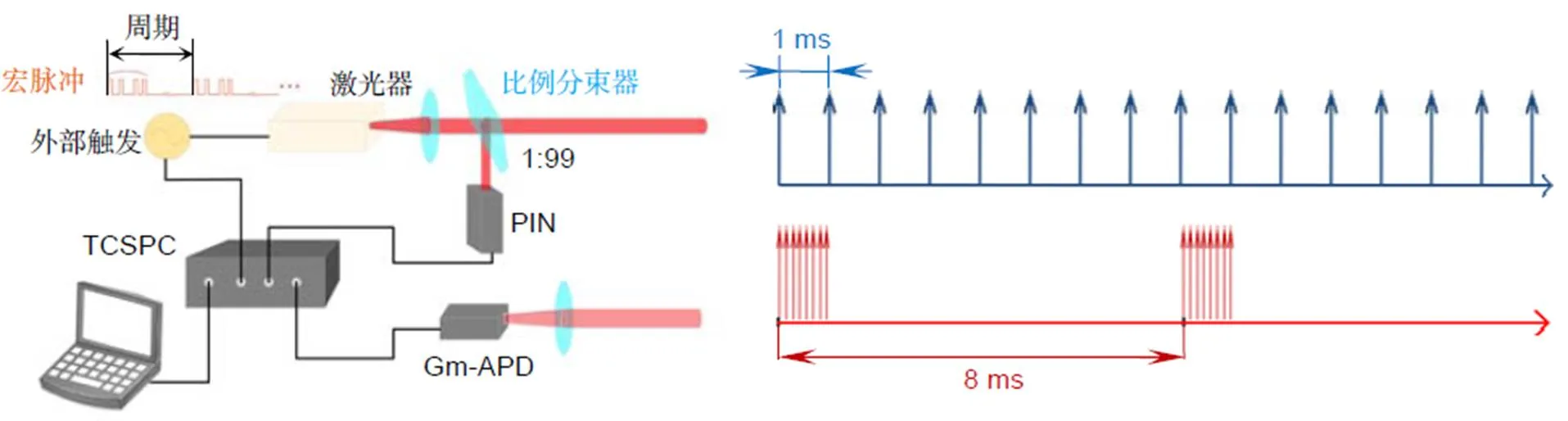
图1 宏/子脉冲编码光子计数激光雷达系统结构
宏/子脉冲光子计数激光雷达采用时移脉冲累加的方法获取目标距离,其中累加的过程与传统的脉冲累加方法一样,目的都是通过累加提高系统的信噪比。
考虑远距离高速运动目标的探测,当目标处于高速运动时,每个脉冲测量到的是不同距离处的目标。目前常见的商用光子计数模块的时间分辨率一般为亚纳秒量级,可以实现亚厘米级的距离分辨。因此,只要每个脉冲间隔内目标的运动距离超过光子计数模块时间分辨率对应的距离分辨率,每个脉冲获得的就是不同的飞行时间,本文使用的SIMINICS-FT1040光子计数模块的时间分辨率为64 ps。定义计数模块的时间分辨率为精时间门,如图3(a)展示的是运动目标在精时间门的情况下多脉冲累加的示意图。红色曲线表示不同周期激光脉冲的飞行时间对应的精时间门的位置。在精时间门的情况下,由于目标的运动,三个周期的回波信号位于不同的时间门,直接在这种精时间门的情况下对三个周期进行累加难以提取出目标的位置。在目标运动速度未知的情况下,为了解决这个问题,需要将系统的时间分辨率降低,目的是使目标在较低的时间分辨率下近似静止。低时间分辨率对应粗的时间门,如图3(b)展示的是运动目标在粗时间门的情况下多脉冲累加的示意图。蓝色实线表示不同周期激光雷达的飞行时间对应的粗时间门的位置。在粗时间门的情况下,由于时间分辨率较低,目标的运动被忽略,不同位置目标的回波位于相同的粗时间门内,因此,可以通过多周期累加的方式提取目标的飞行时间,从而获得目标的距离。
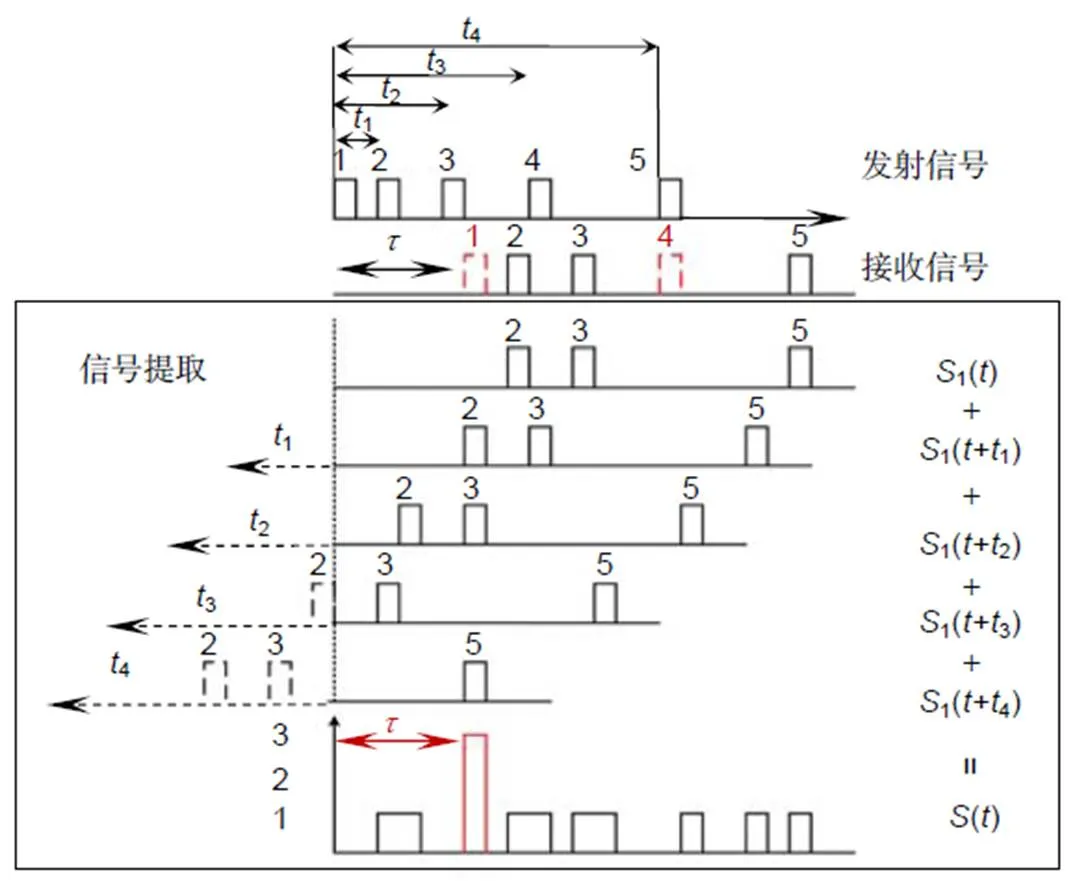
图2 时移脉冲累加飞行时间提取方法
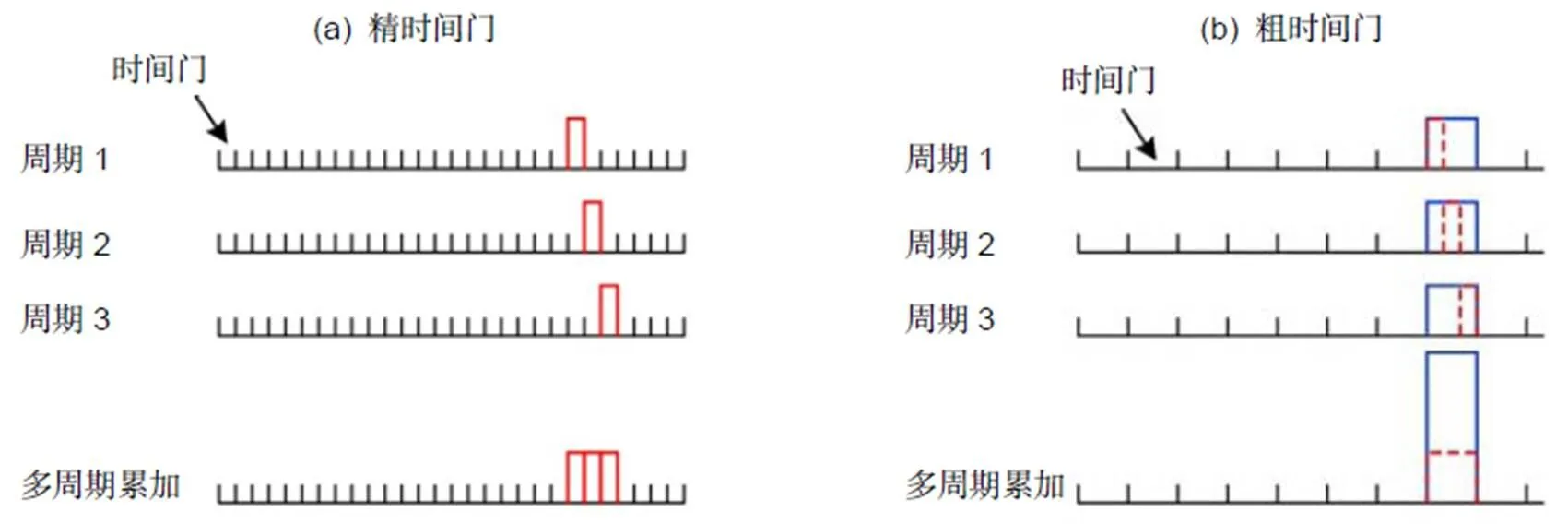
图3 在精时间门(a)和粗时间门(b)的情况下,目标运动对脉冲累加效果的影响
对于宏/子脉冲方法,粗时间门的选择与总的子脉冲间隔、子脉冲宽度以及目标的运动速度相关;而对于脉冲累加方法来说,粗时间门的选取则与激光器的脉冲重复频率(pulse repetition frequency,PRF)、累加脉冲的个数、脉冲宽度、目标的运动速度有关。

需要指出的是,为了减小距离游走误差的影响[21],在计算粗时间门宽度时考虑了脉冲的宽度。
3 宏/子脉冲光子计数激光雷达虚警概率与探测概率分析
为了定量地分析宏/子脉冲光子计数激光雷达与传统脉冲累加光子计数激光雷达测量远距离、高速运动目标的性能,本节将对宏/子脉冲方法的虚警概率以及探测概率进行分析。
3.1 虚警概率分析
当初始电子的数量较少时,Gm-APD探测器的探测模型近似服从泊松分布[22],噪声的概率密度函数可以描述为个噪声雪崩事件发生的概率。在一个时间门内,个噪声雪崩事件发生的概率可以表示为
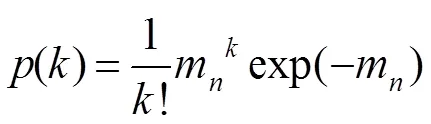

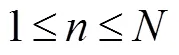
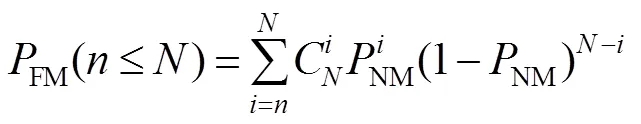
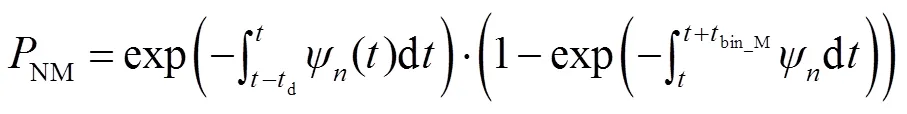
图4展示了当脉冲累加个数为20,探测器死时间为25 ns,时间门宽度为20 ns时,在不同信号识别阈值情况下,虚警概率随噪声计数水平变化的情况。可以发现,当时间门确定时,虚警概率随噪声计数的增加呈指数增长。实际应用中,系统的虚警概率有一个最高阈值的限定。为了满足系统对虚警概率的要求,当噪声计数越高时,需要设置更高的阈值。如图4所示,当噪声计数小于0.55 Mcp时,阈值=3即可以满足系统虚警概率小于0.1%的要求;而当噪声计数分布在0.55 Mcps~1.3 Mcps时,阈值则需要设置为=4。
当时间门宽度一定时,噪声水平自然是影响虚警概率的主要因素。图5展示了当累加脉冲个数为20、探测器死时间为25 ns、噪声计数水平为1 Mcps时,不同信号识别阈值下,虚警概率随时间门宽度变化的情况。可以发现,随着时间门宽的增加,虚警概率呈指数增长。如图5所示,假设系统指标要求虚警概率不大于1%,在图中所示的系统参数下,当时间门宽度为20 ns时,可以设置信号识别阈值=3,而当时间门宽度为50 ns时,则需要设置信号识别阈值=5。
3.2 探测概率分析
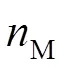
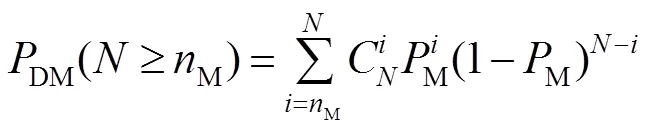
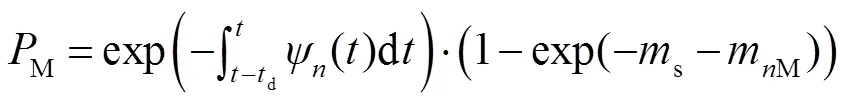
宏/子脉冲方法和脉冲累加方法探测概率的最大区别在于信号识别阈值的不同,因此两种方法可以采用相同的探测概率表示形式。图6展示了当子脉冲个数为20、探测器死时间为25 ns、噪声计数水平为1 Mcps时,在不同信号识别阈值情况下,探测概率随信号初始光电子变化的情况。在同一个信号识别阈值下,与单脉冲探测概率变化的趋势相同,随着平均回波光子数的增加,宏/子脉冲方法的探测概率逐渐增加,并趋于饱和。但是,在探测概率均未饱和的情况下,当信号初始光电子数相同时,信号识别阈值越高,系统的探测概率越低。
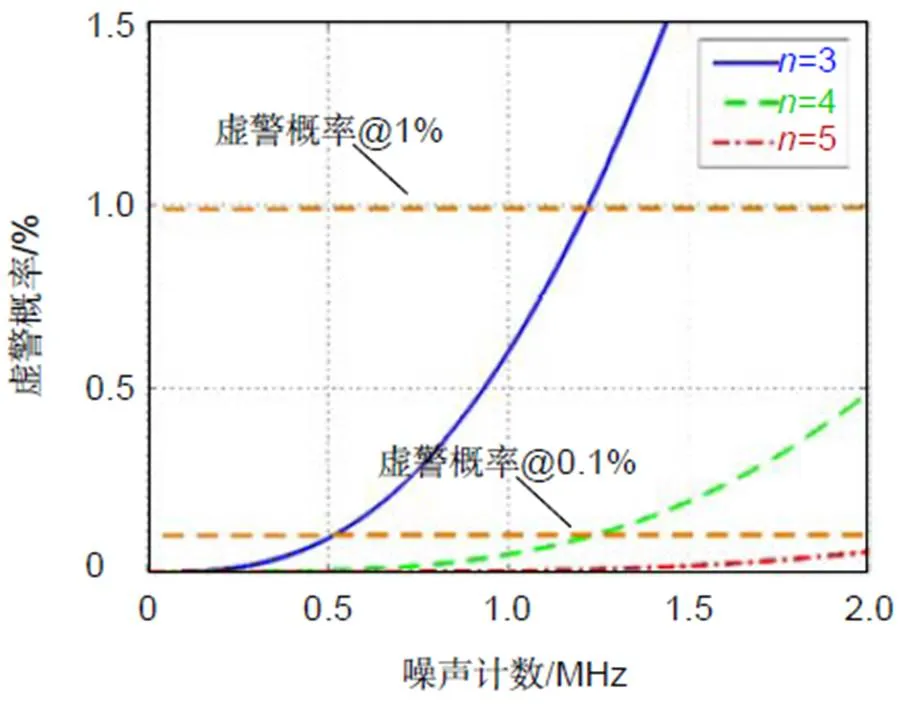
图4 噪声水平对探测概率的影响 (N=20, td=25 ns, tbin=20 ns)

图5 时间门宽度对虚警概率的影响 (N=20, td=25 ns, ψn=1 Mcps)
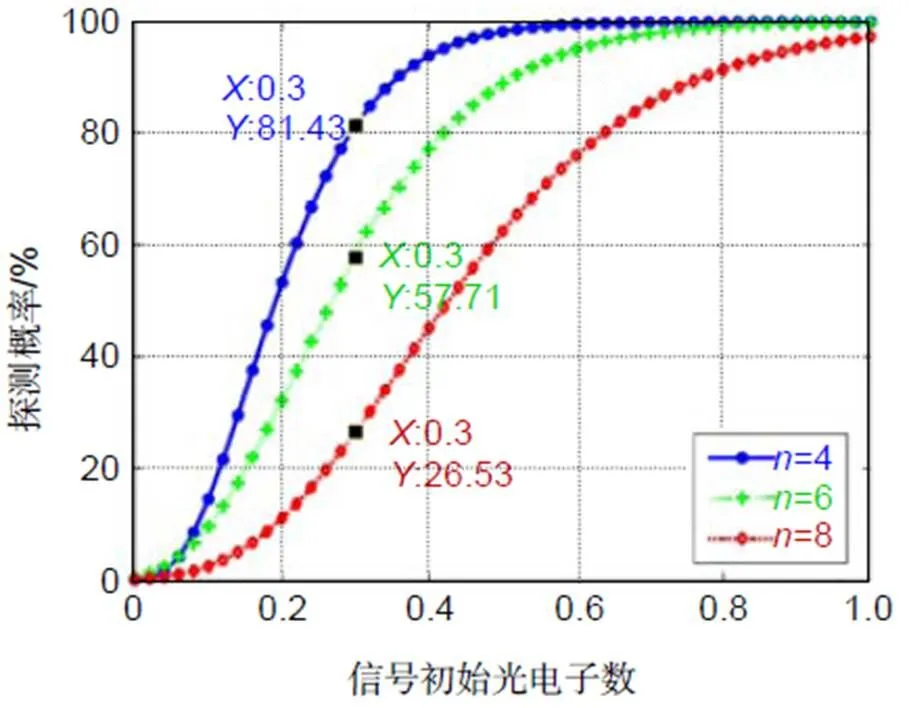
图6 信号识别阈值对探测概率的影响(N=20, td=25 ns, ψn=1 Mcps)
根据图5和图6可以发现,时间门越宽,时间门的虚警概率越高,从而导致系统的虚警概率更高,因此需要选择更高的信号识别阈值以抑制虚警;而信号识别阈值越高,在相同的系统参数下,探测概率越低。在测量高速运动的目标时,因为宏/子脉冲方法可以更集中地发射多个子脉冲,子脉冲的发射持续时间越短,运动目标的回波信号在时域上更集中,因而更容易实现对回波信号的提取。
4 宏/子脉冲光子计数雷达测距仿真与实验验证
4.1 远距离高速运动目标探测仿真
本文采用蒙特卡洛(Monte Carlo)仿真方法来验证宏/子脉冲方法的探测性能。仿真的主要参数如表1所示。
鱼粉的感官评价参考显微镜检验的结果,可以参照国标的方法进行。同时,结合上述感觉评价,可以对鱼粉的质量状态进行定性和半定量的评价和分析。在通过上述感官评价判定为合格之后,再进行化学评价,这也是鱼粉质量控制的基本原则。
在本文中假设目标与激光雷达系统之间仅有径向速度无切向速度,仿真过程通过以下五步来实现:
第一步:根据宏/子脉冲方法的脉冲间隔、目标的初始位置、速度以及运动方向(相向运动或背向运动),计算出每个脉冲与高速运动目标相逢时的飞行时间;
第二步:以泊松分布的方式,根据系统参数以及第一步获得的脉冲飞行时间,在每个时间门内随机产生信号和噪声;
第三步:根据系统参数预先选择合适的粗时间门(粗时间门的选取参照2.2节),并根据选定的粗时间门对第二步获得的数据进行粗值化处理,这一步的目的是为了减小目标运动带来的负面影响;
第四步:在第三步的基础上,根据2.2节提出的时移累加方法将个子脉冲累加;
第五步:根据统计直方图提取信号位置。
在蒙特卡洛仿真中,假设目标从100 km远处向激光雷达系统高速运动,目标仅有径向运动且运动速度为1500 m/s。考虑到距离模糊的问题,设定宏脉冲的重复频率为50 Hz。在每个宏脉冲周期中,20个子脉冲以不等的脉冲间隔分布在1 ms时间内。在1 ms的时间内,目标运动1.5 m,根据式(2),时间门宽度可以设置为15 ns。依次根据仿真的五个步骤,得到了如图7所示的宏/子脉冲方法的累加直方图。
为了验证宏/子脉冲编码光子计数激光雷达的可行性,假设目标以1500 m/s的速度从100 km远处径直飞向激光雷达系统。对目标进行连续2 s仿真探测,宏/子脉冲方法可以提供100个回波位置。分别仿真统计了单脉冲探测概率为30%、40%、50%三种回波强度下,宏/子脉冲方法能够正确提取回波位置的概率(零虚警条件下的探测概率)。在图8中,蓝色的实线代表目标的真实运动轨迹,红色点代表两种方法探测到的目标位置。其中,在蓝色实线上的红点代表目标被正确探测,其他红点则表示目标位置提取错误。由图8可以发现,随着回波强度的增加,宏/子脉冲方法可以更好地恢复目标的运动轨迹。
为了更定量地分析宏/子脉冲方法的探测概率,在三种回波强度下,对上述仿真过程分别重复5次,探测概率的统计结果如表2所示。由表中统计的数据可以发现,在仿真的三种回波信号强度下,宏/子脉冲方法的探测概率逐渐增加并在单脉冲探测概率为40%~50%左右时接近饱和状态。

表1 仿真实验的主要参数
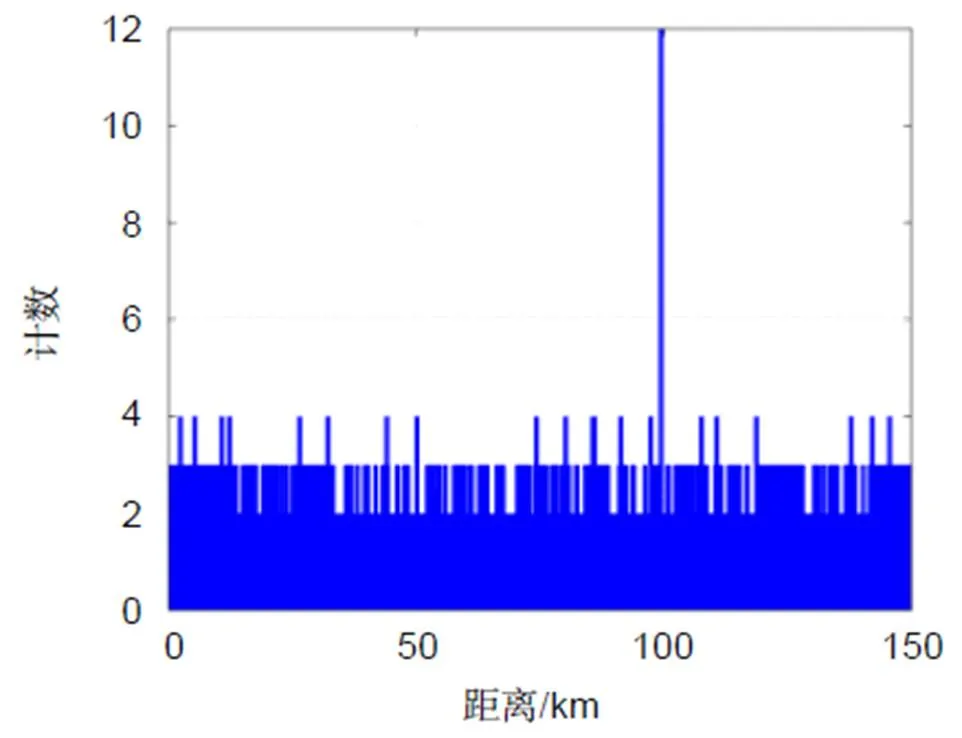
图7 宏/子脉冲方法的累加直方图
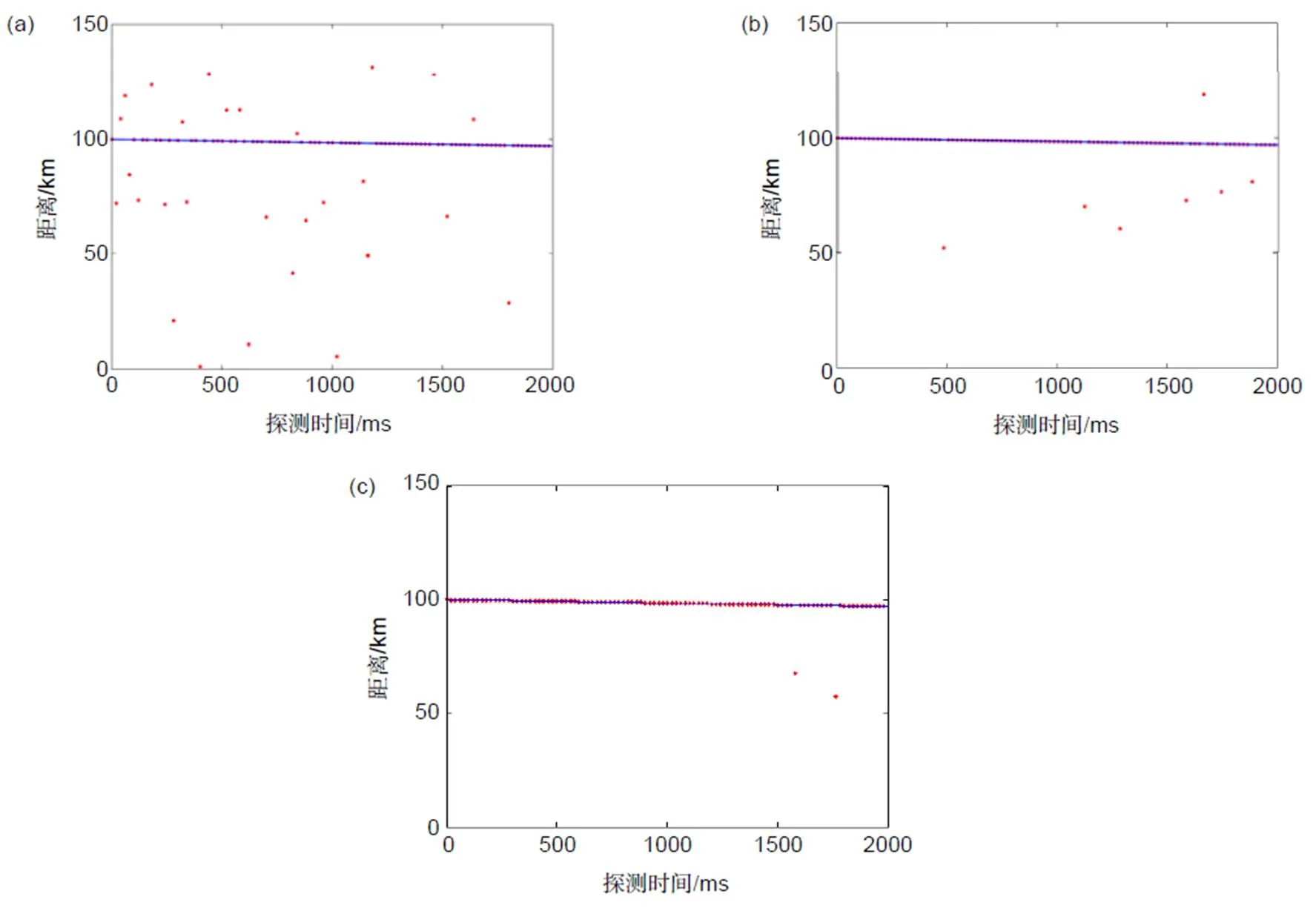
图8 宏/子脉冲方法在不同回波信号强度下的探测仿真结果。(a) 单脉冲探测概率30%;(b) 单脉冲探测概率40%;(c) 单脉冲探测概率50%
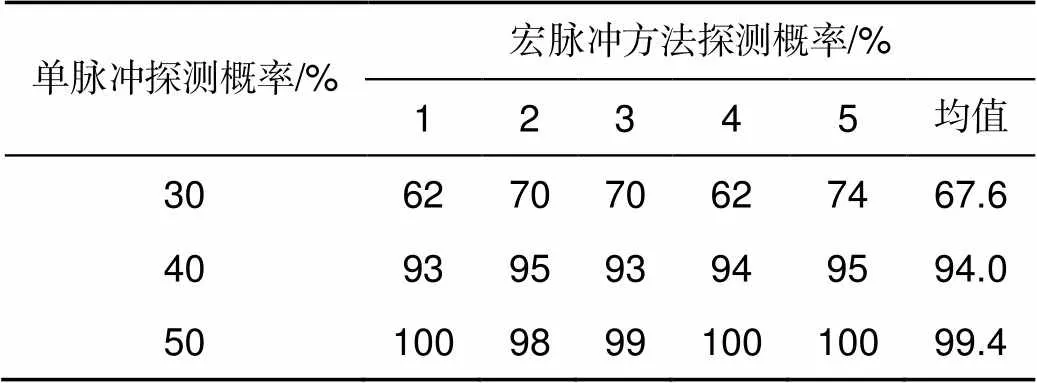
表2 宏/子脉冲方法探测概率仿真结果
4.2 远距离高速运动目标探测实验验证
在完成仿真验证的基础上,搭建了等效远距离高速运动目标的实验平台,进一步完成了实验验证。由于远距离高速运动目标的真实实验场景难以在实验室条件下完成,我们以实验室现有的实验设备,完成了远距离高速运动目标的等效验证。
实验原理图如图9所示,利用实验室频率5 GHz的AWG5002信号发生器和外调制频率10 MHz的激光器,对远距离高速运动平台的回波信号进行构造。构造的过程可以分为三个步骤:首先,由信号发生器的通道1产生一个触发信号直接由光子计数采集卡记录作为计时开始信号;随后以信号发生器通道1作为时序基准,直接由信号发生器的通道2通过延时产生模拟100 km处耦合了目标运动的回波信号电脉冲序列,再由该电脉冲序列直接驱动激光器产生光脉冲序列,此时由激光器产生的光脉冲在时间延迟上等效于100 km远处目标的回波脉冲;最后,考虑距离对激光脉冲能量的衰减,在光脉冲进入Gm-APD探测器之前加入可调光学衰减器(VOA),通过调节VOA的衰减比例,模拟不同距离的回波信号强度。总的来说,通过信号发生器完成对回波信号时域上的模拟,通过VOA完成对回波信号强度上的模拟,最终构造出的光脉冲序列在时域与强度上均与真实远距离目标的回波信号近似。图10为搭建的等效远距离高速运动目标探测平台,实验参数如表3所示。
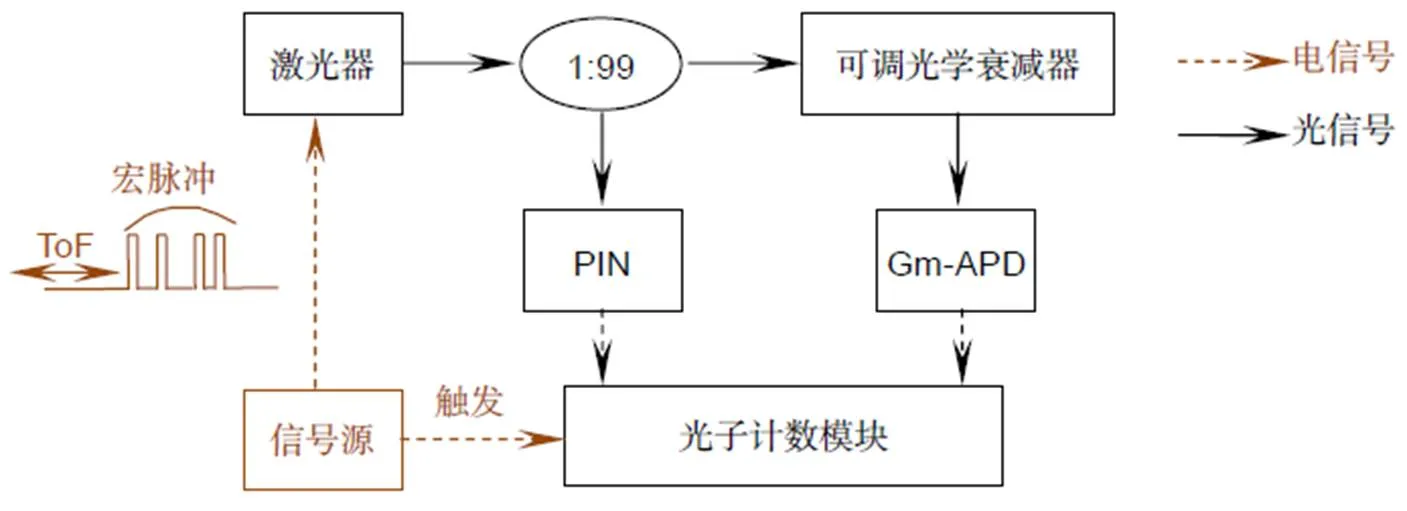
图9 高速运动目标探测实验原理图
带有飞行时间延迟的调制信号可以根据目标的初始距离、目标运动速度和脉冲的周期计算获得。则宏/子脉冲方法中发射的第个宏脉冲的飞行时间可以表示为
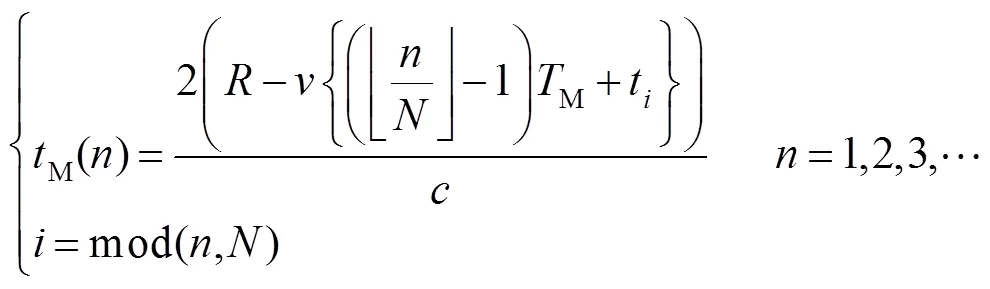
与仿真中使用的参数一样,假设目标以1500 m/s的速度从100 km远处径直飞向激光雷达系统,设置宏脉冲的周期为20 ms。对目标的运动轨迹连续进行2 s的监测,根据式(8)计算宏/子脉冲方法的调制信号,并将调制信号对激光器进行外触发,获得远距离的目标回波,实验中使用的信号发生器可以将脉冲的飞行时间精确到亚纳秒量级。同时,调整VOA的衰减比例,比较不同回波强度(单脉冲探测概率为30%、40%、50%)下两种方法的探测性能。

图10 等效远距离高速运动目标实验平台
与图8类似,图11和表4展示了宏/子脉冲方法在三种不同回波强度下,探测到的高速运动目标的运动轨迹和统计结果。可以发现,在展示的三种回波信号强度下,宏/子脉冲方法的目标跟踪轨迹的仿真结果与实验结果高度一致。
在测量远距离高速运动目标时,宏/子脉冲编码方法以不等的短间隔将多个脉冲以脉冲簇的形式进行集中式发射,这种方法有效地减小了多个脉冲之间的总间隔,因而是一种有效的远距离高速运动目标探测方法。对于高速运动的目标,参与累加的多个脉冲之间的间隔越短,则目标运动的距离越小;根据式(1)可知,目标运动距离越小,需要选择的粗时间门越小;而粗时间门越小,由式(4)可知系统的虚警概率越低;在保证系统满足最大虚警概率要求的前提下,可以选择更小信号识别阈值;而信号识别阈值越小,根据式(6)、式(7)可知,目标的探测概率越高。因此,宏/子脉冲编码方法由于比脉冲累加方法具有更短的脉冲发射间隔,探测概率得以显著提高。
表5统计了宏/子脉冲方法探测概率的理论、仿真以及实验结果,可以发现三者具有极高的一致性;随着单脉冲探测概率的增加,宏/子脉冲的探测概率逐渐增加并趋于饱和,最终通过理论、仿真以及实验验证了宏/子脉冲编码光子计数激光雷达是一种有效的远距离高速径向运动目标探测方法。
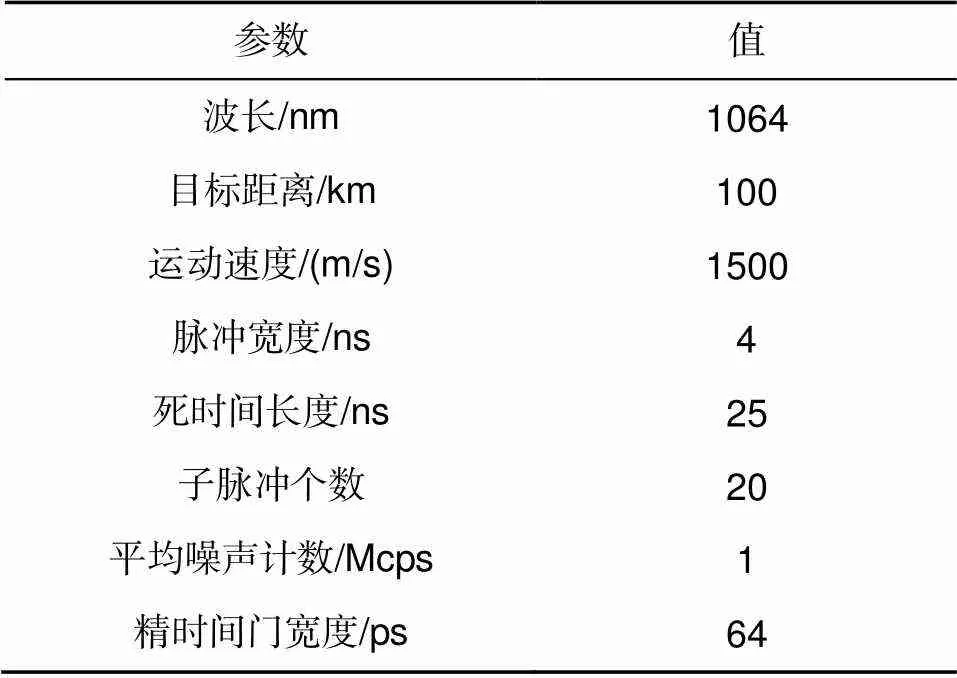
表3 实验系统的主要参数

图11 宏/子脉冲方法在不同回波信号强度下的探测实验结果。(a) 单脉冲探测概率30%;(b) 单脉冲探测概率40%;(c) 单脉冲探测概率50%
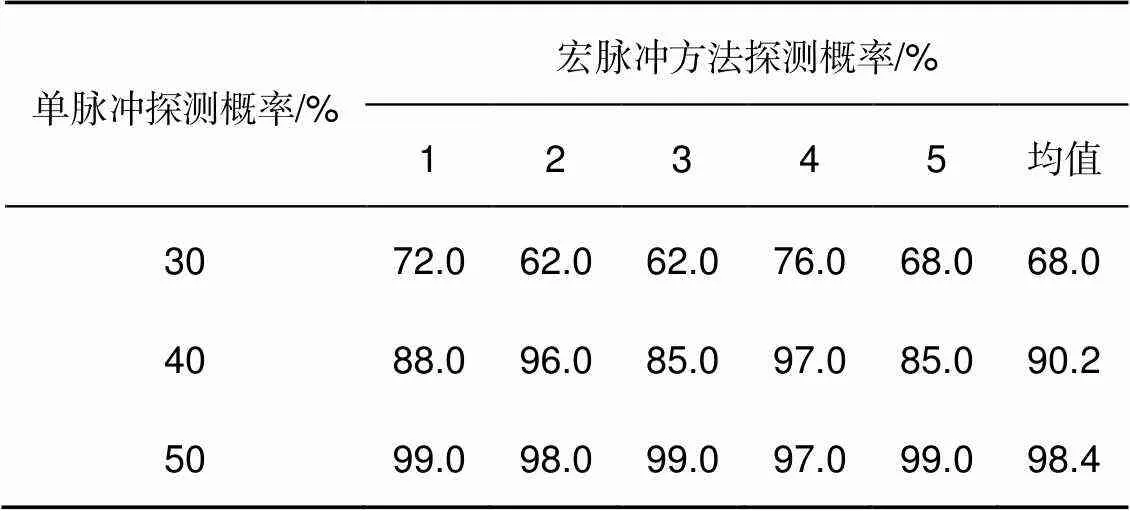
表4 宏/子脉冲方法探测概率实验结果
5 总 结
宏/子脉冲编码光子计数激光雷达是针对远距离且目标与激光雷达平台间存在相对距离变化的应用而提出的方法。与传统脉冲的对比,宏/子脉冲方法采用脉冲串簇发的方式,缩短了光子计数所需累积脉冲的时间间隔。脉冲串的间隔越短,目标的运动越不显著,这一特点使得其对于远距离高速运动目标的探测具有明显的优势。同时子脉冲在相对较短的时间内集中发射,提高了系统的探测速度,可以显著提高对于高速运动目标的测距精度。所提出的方法没有明显的增加系统的复杂度,与传统的脉冲累积方法具有相同的激光平均发射功率,并不增加对系统资源的需求,同时不需要复杂的算法即可以采用常规的方式对回波信号进行提取,因而具有重大的实用价值。
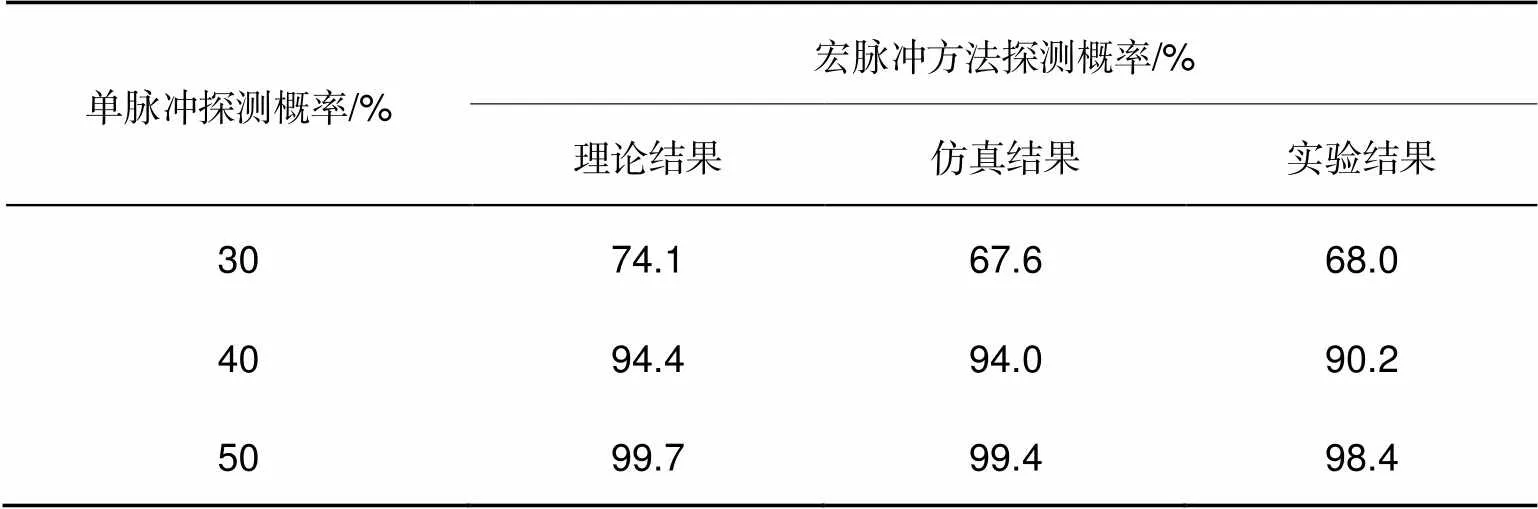
表5 宏/子脉冲方法探测概率
[1] Albota M A, Aull B F, Fouche D G,Three-dimensional imaging laser radars with Geiger-mode avalanche photodiode arrays[J]., 2002, 13(2): 351–370.
[2] Warburton R E, McCarthy A, Wallace A M,Subcentimeter depth resolution using a single-photon counting time-of-flight laser ranging system at 1550 nm wavelength[J]., 2007, 32(15): 2266–2268.
[3] O’Brien M E, Fouche D G. Simulation of 3d laser radar systems[J]., 2005, 15(1): 37–60.
[4] Stone W C, Juberts M, Dagalakis N G,. Performance analysis of Next-Generation ladar for manufacturing, Construction, and Mobility[R]. NIST, 2007: 7112–7117.
[5] Liu B, Yu Y, Jiang S. Review of advances in LiDAR detection and 3D imaging[J]., 2019, 46(7): 190167. 刘博, 于洋, 姜朔. 激光雷达探测及三维成像研究进展[J]. 光电工程, 2019, 46(7): 190167.
[6] Prochazka I, Kodet J, Blazej J,. Photon counting detector for space debris laser tracking and lunar laser ranging[J]., 2014, 54(4): 755–758.
[7] Vacek M, Michalek V, Peca M,. Photon counting Lidar for deep space applications: concept and simulator[J]., 2013, 8773: 877309.
[8] Markus T, Neumann T, Martino A,. The ice, cloud, and land elevation satellite-2 (ICESat-2): science requirements, concept, and implementation[J]., 2017, 190: 260–273.
[9] Liu B, Yu Y, Chen Z,. True random coded photon counting Lidar[J]., 2020, 3(2): 190044.
[10] Mccarthy A, Collins R J, Krichel N J,. Long-range time-of-flight scanning sensor based on high-speed time-correlated single-photon counting[J]., 2009, 48(32): 6241–6251.
[11] Du B C, Pang C K, Wu D,. High-speed photon-counting laser ranging for broad range of distances[J]., 2018, 8(1): 4198.
[12] Liang M, Huang J H, Ren M,. 1550-nm time-of-flight ranging system employing laser with multiple repetition rates for reducing the range ambiguity[J]., 2014, 22(4): 4662–4670.
[13] Zhang Q, Soon H W, Tian H T,. Pseudo-random single photon counting for time-resolved optical measurement[J]., 2008, 16(17): 13233–13239.
[14] Zhang Q, Chen L, Chen N G,. Pseudo-random single photon counting: a high-speed implementation[J]., 2010, 1(1): 41–46.
[15] Takeuchi N, Sugimoto N, Baba H,. Random modulation CW Lidar[J]., 1983, 22(9): 1382–1386.
[16] Hiskett P A, Parry C S, Mccarthy A,. A photon-counting time-of-flight ranging technique developed for the avoidance of range ambiguity at gigahertz clock rates[J]., 2008, 16(18): 13685–13698.
[17] Krichel N J, Mccarthy A, Buller G S. Resolving range ambiguity in a photon counting depth imager operating at kilometer distances[J]., 2010, 18(9): 9192–9206.
[18] Rieger P, Ullrich A. A novel range ambiguity resolution technique applying pulse-position modulation in time-of-flight ranging applications[J]., 2012, 8389: 83790R.
[19] Zhang Y F, He Y, Yang F,. Three-dimensional imaging Lidar system based on high speed pseudorandom modulation and photon counting[J]., 2016, 14(11): 111101.
[20] Yang F, Zhang F, He F,. High speed pseudorandom modulation fiber laser ranging system[J]., 2014, 12(8): 082801.
[21] Oh M S, Kong H J, Kim T M,. Reduction of range walk error in direct detection laser radar using a Geiger mode avalanche photodiode[J]., 2010, 283(2): 304–308.
[22] Gatt P, Johnson S, Nichols T,. Geiger-mode avalanche photodiode ladar receiver performance characteristics and detection statistics[J]., 2009, 48(17): 3261–3276.
Macro/sub-pulse coded photon counting LiDAR
Liu Bo1,2,3*, Jiang Shuo1,2,3, Yu Yang4, Chen Zhen1,2
1Key Laboratory of Science and Technology on Space Optoelectronic Precision Measurement, Chinese Academy of Sciences, Chengdu, Sichuan 610209, China;2Institute of Optics and Electronics, Chinese Academy of Sciences, Chengdu, Sichuan 610209, China;3University of Chinese Academy of Sciences, Beijing 100049, China;4Institute of Oceanographic Instrumentation, Qilu University of Technology (Shandong Academy of Sciences), Qingdao, Shandong 266001, China

Structure of macro/sub-pulse coded photon counting LiDAR system
Overview:The photon counting LiDAR plays an important role in the long distance measurement because of the high sensitivity to a single photon and the ability of providing accurate photon arrival time. It uses statistical sampling technology which needs to accumulate enough photon events to establish a statistical histogram and extract echo information through the histogram. However, the process will greatly reduce the measurement speed of the system. If there is a relative movement between the system and target, the laser pulses of multiple cycles will have different flight time. Then it can be difficult to extract the distance of the target as the echo signals are difficult to reflect the clustering characteristics in time. In order to solve this problem, a macro/sub-pulse coded photon counting LiDAR is proposed. The measurement speed of the macro/sub-pulse method is determined by the total time of all sub-pulses in the period. Compared with pulse accumulation, the macro/sub-pulse method can realize fast measurement. In the system, the emitting pulse is divided into two parts by a proportional beam splitter, one part is directly detected by PIN and used as the transmitting reference signal, and the other part is used to detect targets. Echo signals scattered by the target are received by optical system and detected by GM-APD (Geiger-mode avalanche photodiode). It should be pointed out that in the macro/sub-pulse LiDAR system, any two sub-pulses have different pulse intervals, which can effectively avoid distance blur. In this paper, the theoretical model of macro/sub-pulse coded photon counting LiDAR is established. To obtain the distance of the target, a method which accumulates the sub-pulses with different time shift operations was proposed in this article. For the time-shifted pulse accumulation method, there is no special requirement for the received signal, but the sub-pulse interval of the transmitted signal needs to be known in advance. To meet this requirement, a PIN detector is used to record the transmitting sequence. Within a period, the echo signals detected by GM-APD detector are shifted sequentially according to the interval of sub-pulses, and the sequentially shifted echo signals are accumulated. The position of the cumulative peak corresponds to the flight time of the sub-pulse. Also, in the third part of this article, the influence of false alarm probability and detection probability were analyzed. The effectiveness of macro/sub-pulse coded photon counting LiDAR is verified by Monte Carlo simulation and experiment.
Citation: Liu B, Jiang S, Yu Y,. Macro/sub-pulse coded photon counting LiDAR[J]., 2020,47(10): 200265
Macro/sub-pulse coded photon counting LiDAR
Liu Bo1,2,3*, Jiang Shuo1,2,3, Yu Yang4, Chen Zhen1,2
1Key Laboratory of Science and Technology on Space Optoelectronic Precision Measurement, Chinese Academy of Sciences, Chengdu, Sichuan 610209, China;2Institute of Optics and Electronics, Chinese Academy of Sciences, Chengdu, Sichuan 610209, China;3University of Chinese Academy of Sciences, Beijing 100049, China;4Institute of Oceanographic Instrumentation, Qilu University of Technology (Shandong Academy of Sciences), Qingdao, Shandong 266001, China
Photon counting LiDAR plays an important role in the long-distance target measurement because of the high detection sensitivity. For the targets with high radial velocity and long distance, ordinary photon counting LiDAR could not recover the useful echo information simply by statistical histogram. In order to solve this problem, a method based on macro/sub-pulse coded photon counting LiDAR is proposed. The flight time of the subpulses is extracted by time shift pulse accumulation and the target distance information is obtained in one macro pulse. In this paper, the theoretical model of macro/sub-pulse coded photon counting LiDAR is established, and the influence of false alarm probability and detection probability is analyzed. The effectiveness of the LiDAR is verified by Monte Carlo simulation and actual experiments.
macro/sub-pulse; LiDAR; photon counting; target measurement
TN958.98;TP23
A
刘博,姜朔,于洋,等. 宏脉冲编码光子计数激光雷达[J]. 光电工程,2020,47(10): 200265
10.12086/oee.2020.200265
: Liu B, Jiang S, Yu Y,Macro/sub-pulse coded photon counting LiDAR[J]., 2020, 47(10): 200265
2020-07-16;
2020-09-28
刘博(1979-),男,博士,研究员,主要从事激光雷达探测与通信的研究。E-mail:boliu@ioe.ac.cn
* E-mail: boliu@ioe.ac.cn

