基于正交试验的短管蜂窝夹套结构应力强度影响因素分析
史为帅,董金善,张力群,李 川
(南京工业大学 机械与动力工程学院,江苏 南京 211816)
20世纪90年代出现了一种高效新型夹套——蜂窝夹套[1-2]。蜂窝夹套以整体夹套为基础,将内筒体与蜂窝底部的小圆孔焊接在一起,构成蜂窝状结构。夹套结构中大量的拉撑件能够加强夹套整体结构的强度及刚度,同时还具有对流体流动的干扰作用。因此相比起其他夹套,蜂窝夹套结构的壁厚可适当减薄[3-4],传热效果和承压能力均更高[5-11]。文中针对三角形排列方式短管蜂窝夹套,设计出正交试验方案,采用极差分析方法、方差分析方法和响应面分析方法处理试验数据,研究单个和多个短管结构参数对夹套强度的影响。
1 短管蜂窝夹套结构研究对象
根据整体模型的对称性和应力强度分析针对的重点结构,创建正三角形排列短管蜂窝夹套的短管、内筒体及外夹套1/4简化模型(图1),通过有限元参数化建模得到多组模型并进行应力分析,提取危险截面一次局部薄膜应力PL以及一次应力+二次应力PL+Pb+Q。

图1 三角形排列短管蜂窝夹套1/4简化模型
2 单个短管结构参数影响试验设计与研究
2.1 试验方案设计与试验数据
2.1.1因素和水平选取
正交试验是分析多个因素以及多个水平的常见设计方法,在工程中涉及到某参数最优解分析时常常用到[12]。根据蜂窝夹套上短管的结构特征,选取4个因素变量建立4水平因素表,见表1。表1中t为短管厚度,s为短管轴向间距,l为短管长度,d为短管直径。
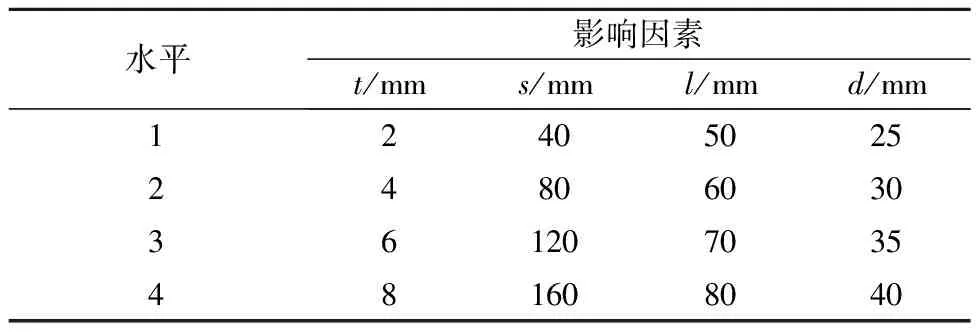
表1 短管4因素-4水平正交试验表
2.1.2试验方案与数据
采用ANSYS软件参数化建模,在数值模拟确定的短管蜂窝夹套结构危险区进行线性化路径分析,获得一次局部薄膜应力PL及一次应力+二次应力PL+Pb+Q。对于每个影响因素,每个水平试验重复4次,共获得16组试验数据,其中t的L16(45)试验方案和数据见表2。短管轴向间距s、短管长度l和短管直径d分析得到的L16(45)试验数据与短管厚度t的类似。
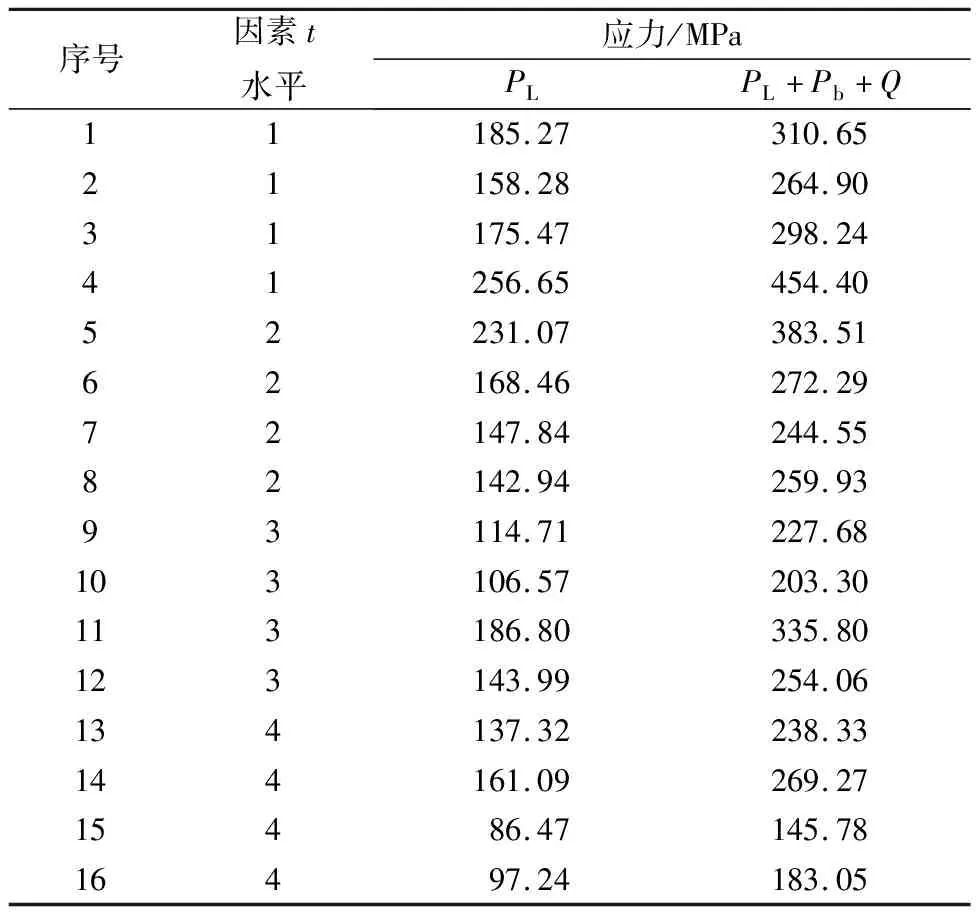
表2 短管厚度t的L16(45)试验方案和数据
2.2 应力试验数据处理与分析
2.2.1极差分析方法
采用极差分析方法对正交试验得到的PL和PL+Pb+Q数据进行极差分析,分析结果分别见表3和表4。表3中与t对应的K1、K2、K3、K4依次为表2中各自的4个PL(分别对应序号1~4、5~8、9~12、13~16)相加所得,即K1=185.27+158.28+175.47+256.65=775.67(MPa),K2=231.07+168.46+147.84+142.94=690.31(MPa),K3=114.71+106.57+186.80+143.99=552.07(MPa),K4=137.32+161.09+86.47+97.24=482.12(MPa)。k1=K1/4,k2=K2/4,k3=K3/4,k4=K4/4。k1、k2、k3、k4中最大值与最小值之差为极差。表3中短管轴向间距s、短管长度l及短管直径d的极差分析过程与短管厚度t的类似,表4中数据的分析过程与表3中的类似。
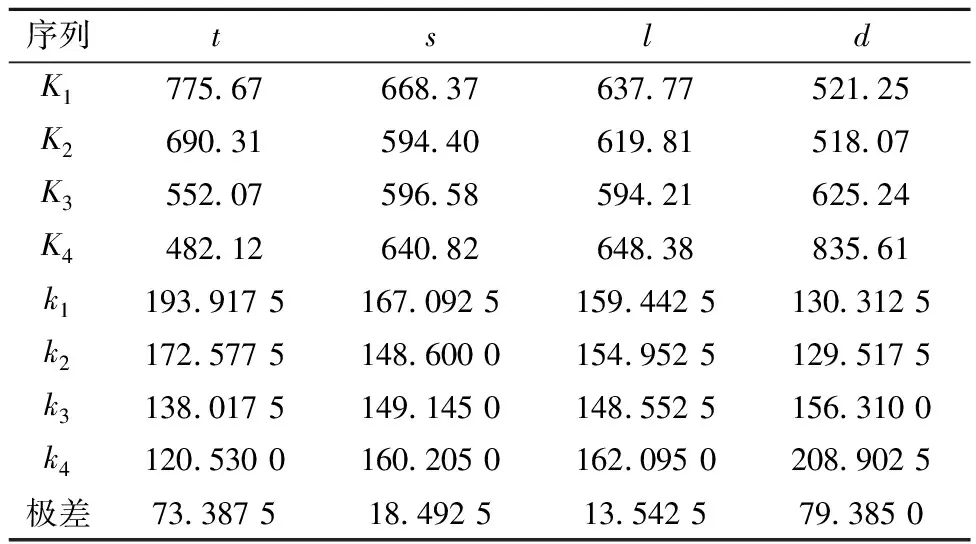
表3 PL试验数据极差分析结果 MPa

表4 PL+Pb+Q试验数据极差分析结果 MPa
极差代表着各因素水平对试验结果的影响,极差越大说明对结果指标影响越大。由表3可知,t、s、l、d的极差分别为73.387 5、18.492 5、13.542 5、79.385 0 MPa,其中因素d的极差最大,因素l的极差最小,这表明因素d在改变水平时,对结构危险截面处应力的影响最大,而因素l对试验指标影响最小。
由表4可知,t、s、l、d的极差分别为122.940 0、37.602 5、23.082 5、130.830 0 MPa。可以看出因素d的极差最大,因素l极差最小,表明因素d在改变水平时对结构危险截面处应力的影响最大,因素l对试验指标的影响最小。根据表3和表4中短管结构参数t、s、l、d各自对应的k1、k2、k3、k4,做4因素水平对PL和PL+Pb+Q影响趋势图,分别见图2~图4。
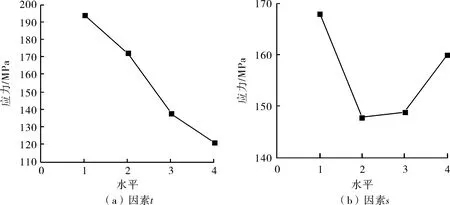
图2 不同因素水平对一次局部薄膜应力PL影响趋势图

图3 因素t和因素s水平对一次应力+二次应力PL+Pb+Q影响趋势图
由图2可知,因素t在4水平时对应的应力最小,因素s在2水平时对应的应力最小,因素l在3水平时对应的应力最小,因素d在2水平时对应的应力最小,结合表3中各因素的极差进行排序,各因素水平对结构危险截面一次局部薄膜应力影响的最佳方案为d2t4s2l3。
由图3和图4可知,因素t在4水平时对应的应力最小,因素s在2水平时对应的应力最小,因素l在2水平时对应的应力最小,因素d在2水平时对应的应力最小,结合表3中各因素的极差进行排序,各因素水平对结构危险截面一次应力+二次应力影响的最佳方案为d2t4s2l2。
2.2.2方差分析方法
对表2中得到的一次薄膜应力PL和一次应力+二次应力PL+Pb+Q正交试验数据采用精度更高的方差法进行分析,结果分别见表5和表6。表5和表6中SS、df、MS、F和P分别表示总偏差平方、自由度、方差、统计量和概率值,其数值的计算参照文献[13]。

表5 一次局部薄膜应力试验数据方差分析结果 MPa

表6 一次应力+二次应力试验数据方差分析结果 MPa
由表5可以知道,影响因素d、s、t的概率值P均小于0.05,表明这3个因素对危险截面一次局部薄膜应力影响是统计显著的,显著性排序为d>t>s>l。
由表6可知,d、t、s的概率值P均小于0.05,表明这3个因素对危险截面一次应力+二次应力影响也是统计显著的,显著性排序为d>t>s>l。
极差分析结果表明,影响危险截面一次局部薄膜应力和一次应力+二次应力的显著水平排序与方差分析的排序结果相同,均为d>t>s>l,因此两者具有相关性。
3 多个短管结构参数对应力强度影响数据研究
3.1 试验方案设计与试验数据
危险截面PL和PL+Pb+Q校核合格是保证设计安全的重要指标[14]。采用响应面法对受s、d、t、l等参数影响的危险截面的PL和PL+Pb+Q数据进行拟合。根据响应面中二阶设计常用的中心组合试验设计(Central Composite Design,简称CCD)方法[15]完成中心组合试验设计,得到的因素组合见表7。

表7 中心组合试验设计因素组合
采用软件Design-Expert,自变量设置为厚度x1、轴向间距x2、长度x3以及直径x4等短管结构参数,响应值设置为一次局部薄膜应力y1及一次应力+二次应力y2,得到中心组合试验因素-水平正交表,见表8。

表8 中心组合试验因素-水平正交表
按照表8的试验设计参数,在Design-Expert软件中输入数据并计算中心组合试验各方案设计条件下短管蜂窝夹套危险截面的一次局部薄膜应力y1以及一次应力+二次应力y2,总共得到30组响应值,部分试验结果见表9。

表9 中心组合试验方案设计以及部分试验结果
3.2 中心组合试验数据处理与分析
3.2.1一次局部薄膜应力
对中心组合试验数据进行拟合,得到一次局部薄膜应力的多元二次回归方程:
y1=31.152+5.623x1+0.141x2-0.241x3+1.758x4+6.914×10-3x1x2+0.044x1x3-0.444x1x4-2.277×10-3x2x3-4.241×10-3x2x4-0.013x3x4-0.335x12+2.206×10-4x22+4.593×10-3x32+ 0.122x42
(1)
参照文献[13]对式(1)进行方差分析,结果见10和表11。表10中,P值反映该回归模型及各因素的显著水平,0.01 表10 一次局部薄膜应力的二次响应回归模型方差分析结果1 表11 一次局部薄膜应力的二次响应回归模型方差分析结果2 由表10可知,x1x4以及x42为显著影响的模型参数,而x1以及x4为极显著影响的模型参数。由表11可知,该模型的决定系数为0.973 649 1,而校正决定系数为0.949 054 9,这表明了5.09%的一次局部薄膜应力变异是不能通过该回归模型解释说明的,有着较高的可信度。其中变异系数为5.08%,说明模型能很好地反映真实的试验值。 3.2.2一次应力+二次应力 依据中心组合试验数据计算结果,拟合得到一次应力+二次应力的多元二次回归方程: y2=22.113+26.005x1+0.230x2+2.429x3-2.643x4-0.020x1x2-0.035x1x3-1.228x1x4-2.85×10-3x2x3-2.76×10-3x2x4-9.10×10-3x3x4-0.052x12-6.99×10-4x22-0.014x32+0.282x42 (2) 对式(2)进行方差分析,得到的结果见表12和表13。表12中P值划分及其表示的显著性程度含义同表10中。 表12 一次应力+二次应力的二次响应回归模型方差分析结果1 表13 一次应力+二次应力的二次响应回归模型方差分析结果2 由表12可知,x1x4及x42代表着显著影响的模型参数,x1以及x4代表着极显著影响的模型参数。由表13可知,该模型的决定系数为0.939 2,而校正决定系数为0.882 4,表明了11.76%的一次应力+二次应力变异是不能通过该回归模型解释说明的,有着较高的可信度。其中变异系数为6.4%,反映了试验值的可靠性。 用回归模型的预测值和观察值作图,得到一次局部薄膜应力、一次应力+二次应力的预测值和实际值分布图、残差正态概率分布图,分别见图5~图6。其中,预测值由式(1)、式(2)得到,观察值由中心组合试验的试验结果得到,残差为回归模型预测值与观察值之差。 图5 应力回归模型预测值和实际值分布情况 图6 应力回归模型残差正态概率分布图 图6中,残差各个散点均在同一条直线上或在其附近排列,表明本次试验的残差是正态分布的,进一步说明该响应面拟合的模型具有可行性。图5中的应力预测值以及实际值的分布规律也是类似的,各个散点均在同一条直线上或在其附近排列,该模型可靠,可以用作预测试验模型。 根据数据的方差分析,进一步得到等高线以及3D响应面图,等高线图的形状大致是圆形或椭圆形,当形状为椭圆形时,交互作用是显著的;当形状为圆形时,交互作用是不显著的[16-18]。各个因素相互作用下一次局部薄膜应力、一次应力+二次应力的等高线以及3D响应面图见图7~图30。由图7~图18可知,因素x1和x4在交互作用下对一次局部薄膜应力影响是显著的,其余因素交互作用均不显著。由图19~图30可知,因素x1和x4在交互作用下对一次应力+二次应力影响是显著的,其余因素交互作用均不显著。 图7 因素x1以及x2相互作用的一次局部薄膜应力等高线图 图8 因素x1以及x2相互作用的一次局部薄膜应力3D响应面图 图9 因素x1以及x3相互作用的一次局部薄膜应力等高线图 图10 因素x1以及x3相互作用的一次局部薄膜应力3D响应面图 图11 因素x1以及x3相互作用的一次局部薄膜应力等高线图 图12 因素x1以及x4相互作用的一次局部薄膜应力3D响应面图 图13 因素x2以及x3相互作用的一次局部薄膜应力等高线图 图14 因素x2以及x3相互作用的一次局部薄膜应力3D响应面图 图15 因素x2以及x4相互作用的一次局部薄膜应力等高线图 图16 因素x2以及x4相互作用的一次局部薄膜应力3D响应面图 图17 因素x3以及x4相互作用的一次局部薄膜应力等高线图 图18 因素x3以及x4相互作用的一次局部薄膜应力3D响应面图 图19 因素x1以及x2相互作用的一次应力+二次应力等高线图 图20 因素x1以及x2相互作用的一次应力+二次应力3D响应面图 图21 因素x1以及x3相互作用的一次应力+二次应力等高线图 图22 因素x1以及x3相互作用的一次应力+二次应力3D响应面图 图23 因素x1以及x4相互作用的一次应力+二次应力等高线图 图25 因素x2以及x3相互作用的一次应力+二次应力等高线图 图26 因素x2以及x3相互作用的一次应力+二次应力3D响应面图 图27 因素x2以及x4相互作用的一次应力+二次应力等高线图 图28 因素x2以及x4相互作用的一次应力+二次应力3D响应面图 图29 因素x3以及x4相互作用的一次应力+二次应力等高线图 图30 因素x3以及x4相互作用的一次应力+二次应力3D响应面图 基于正交试验方法,应用极差分析方法、方差分析方法、响应面分析方法,研究了单个和多个短管结构参数(厚度t、轴向间距s、长度l、直径d)对蜂窝夹套应力强度的影响。研究结果表明,单个短管结构参数因素对蜂窝夹套应力强度的影响程度排序为d>t>s>l。研究得到了一次局部薄膜应力和一次应力+二次应力的多元线性回归方程,可为工程设计提供参考。

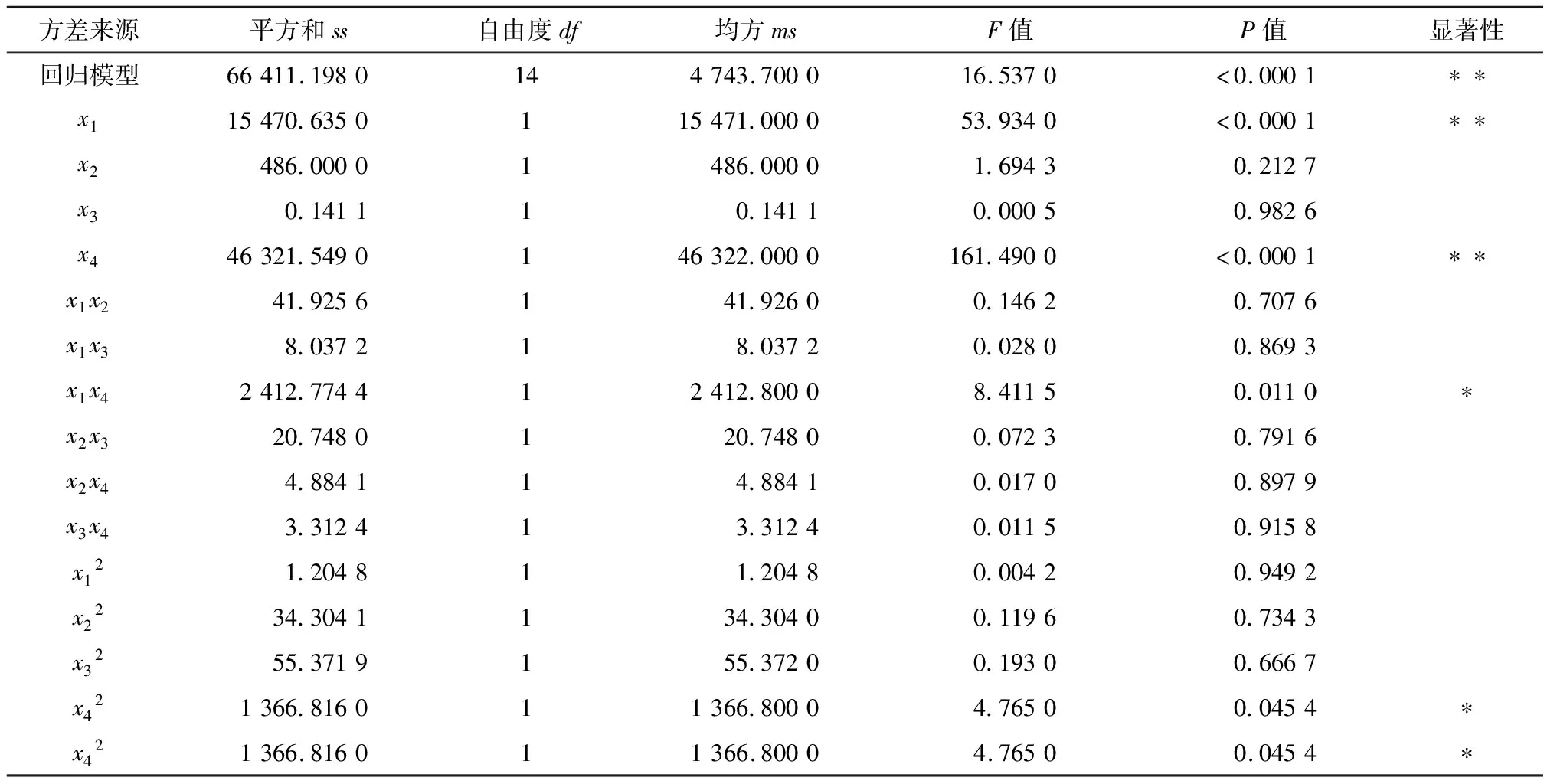

3.3 设计模型准确性验证


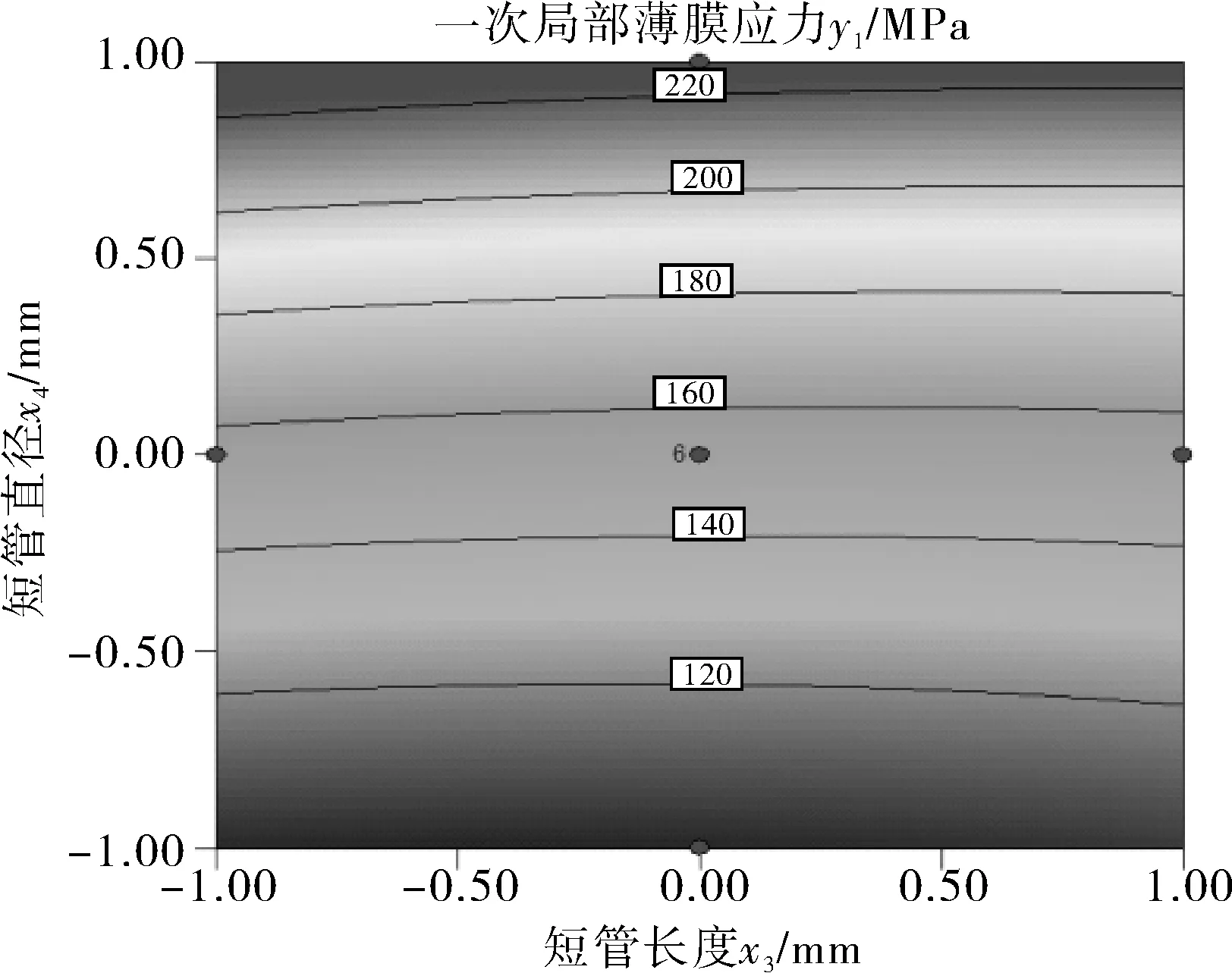
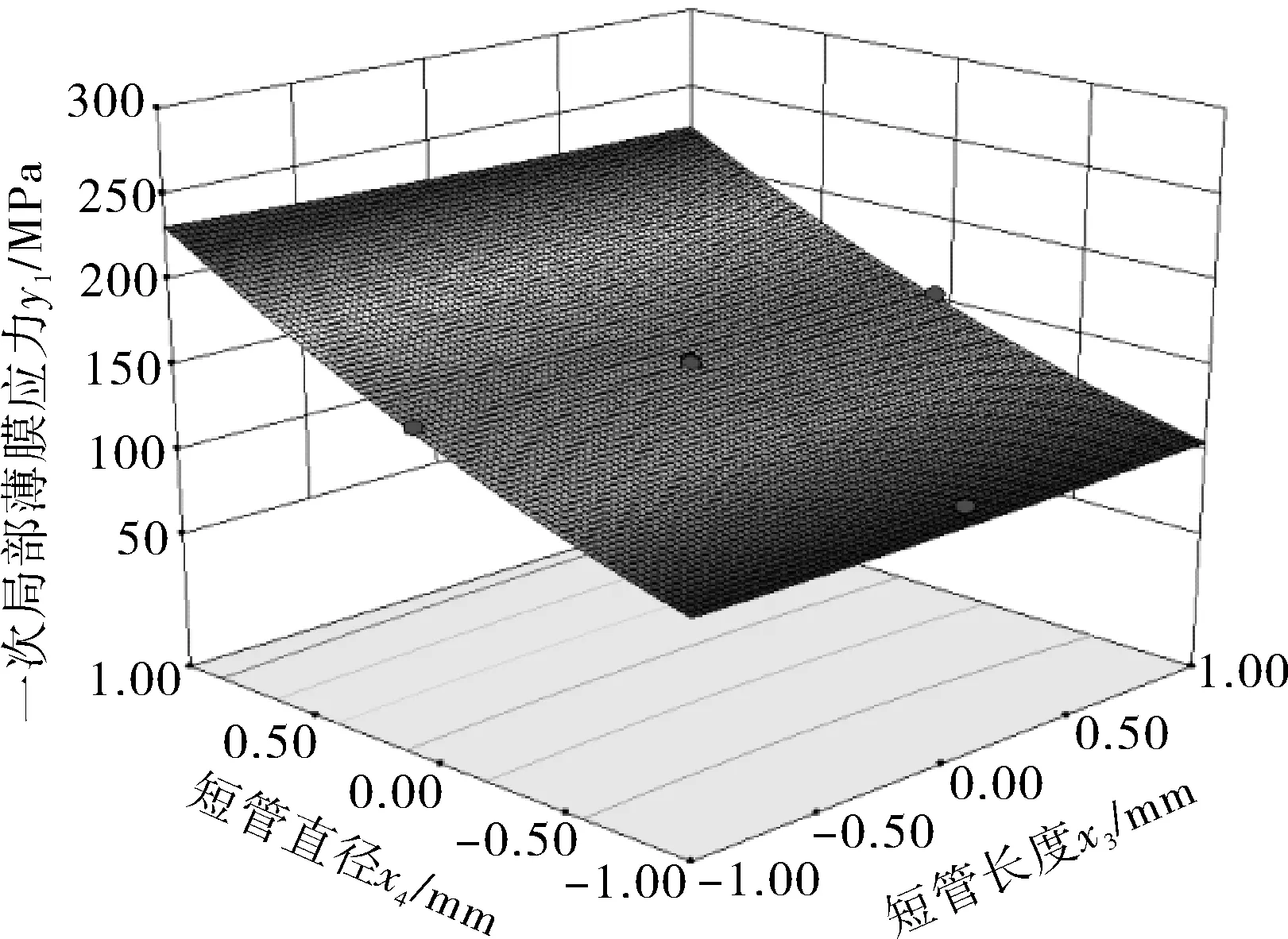
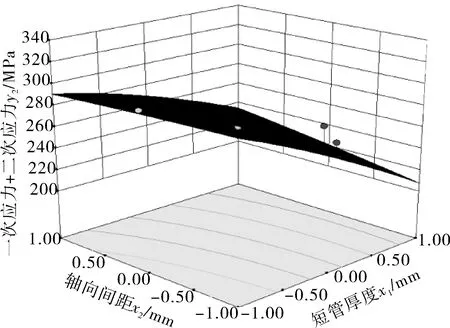
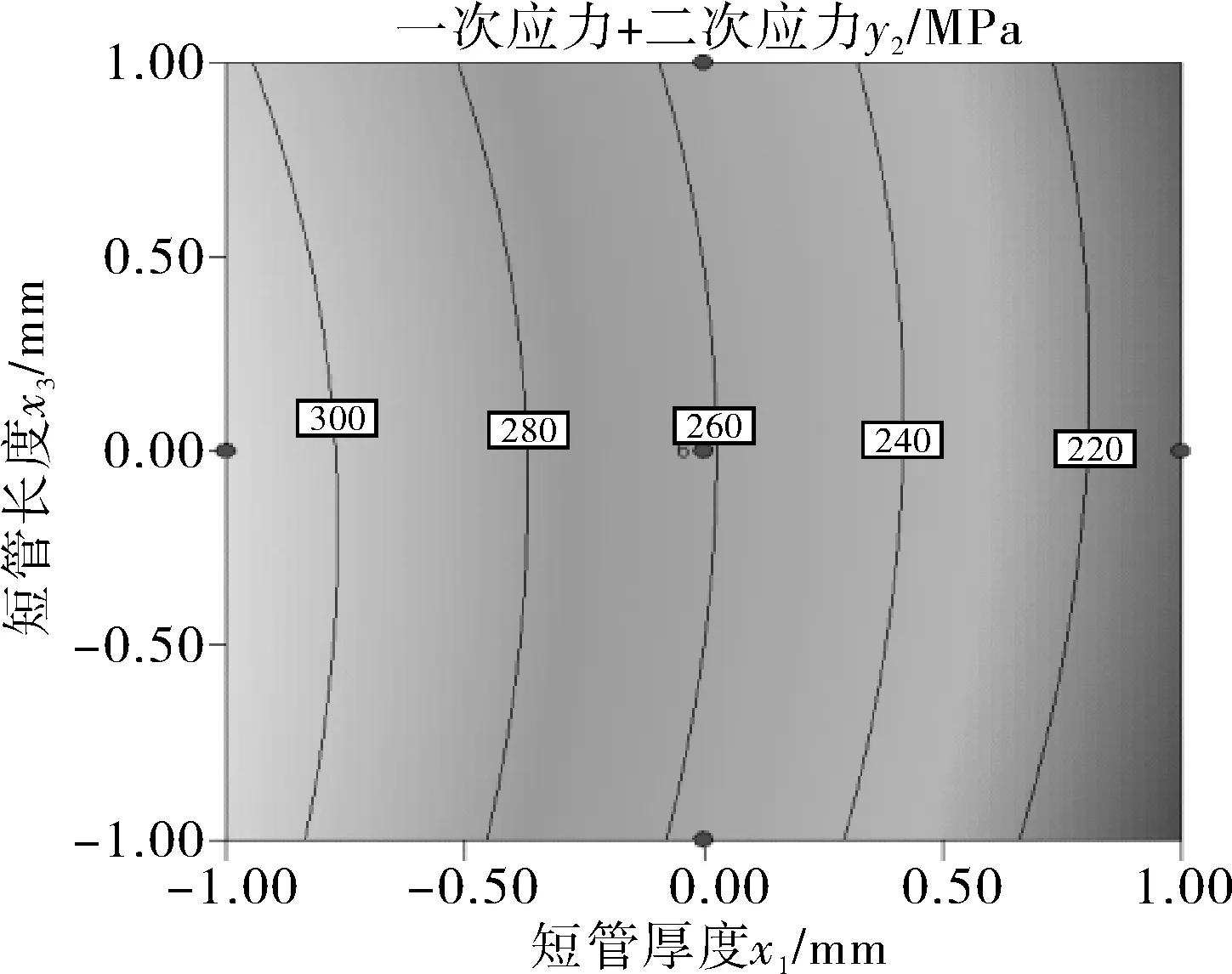
3.4 等高线以及3D响应面分析


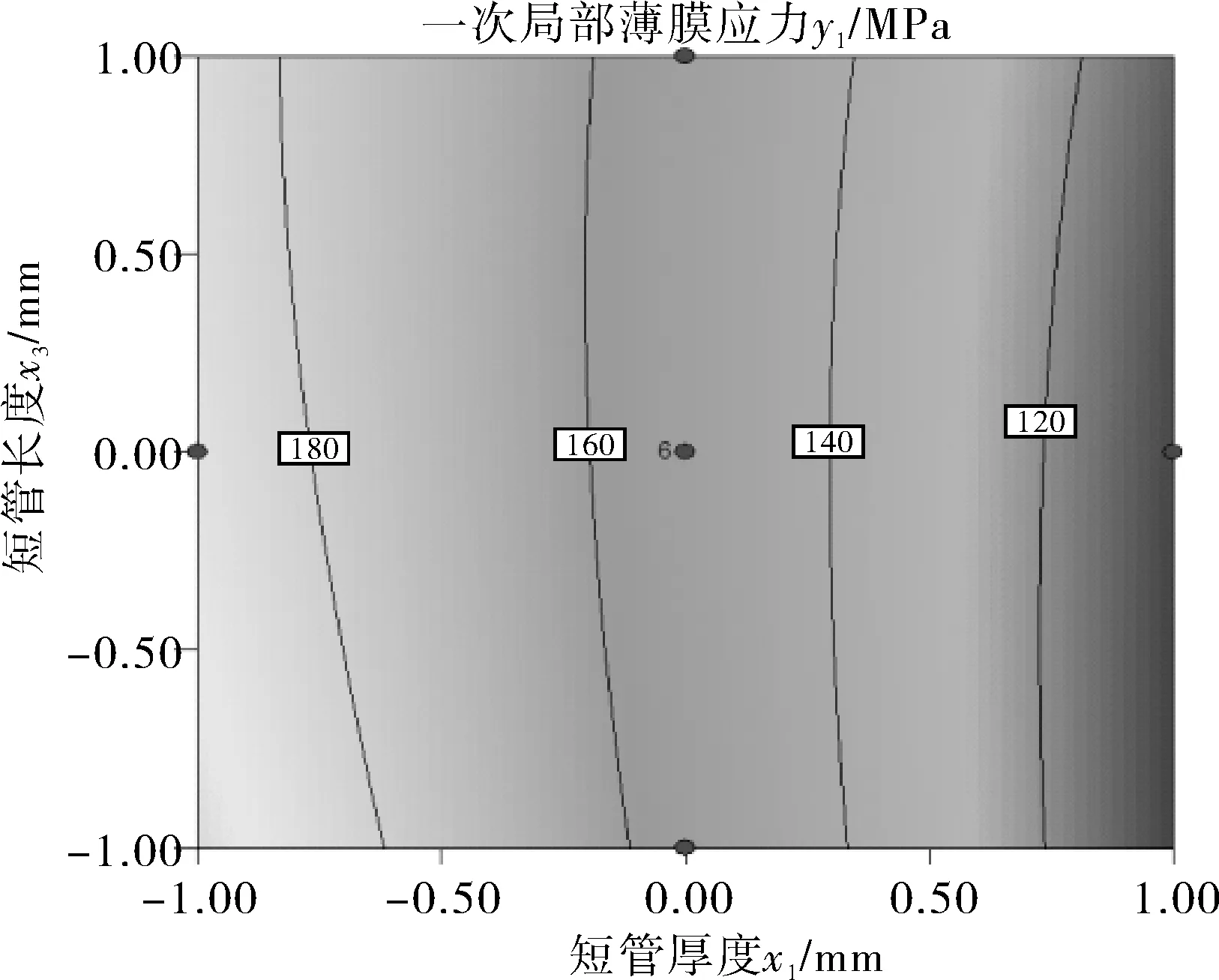
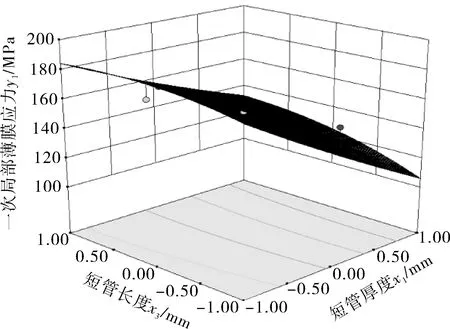
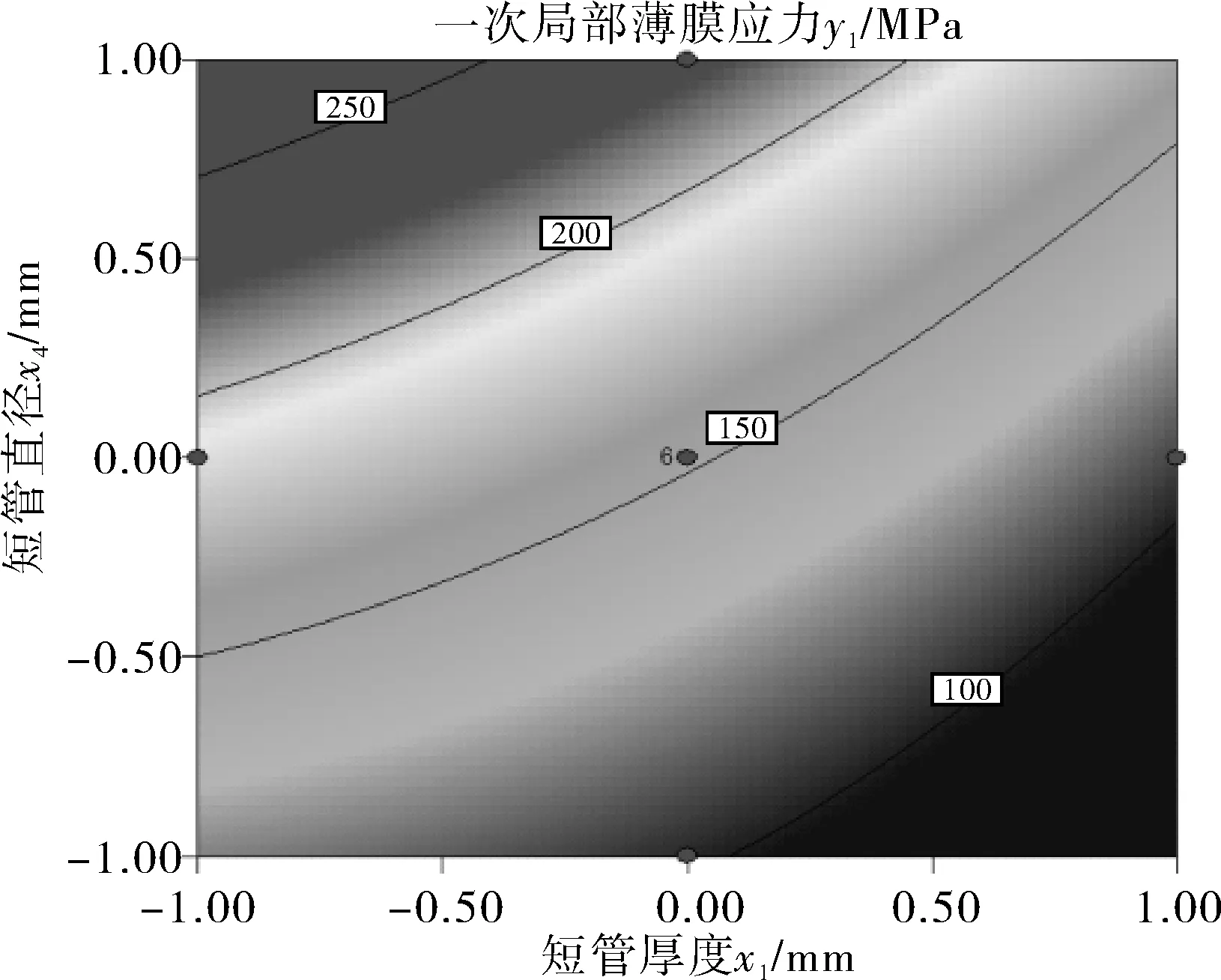
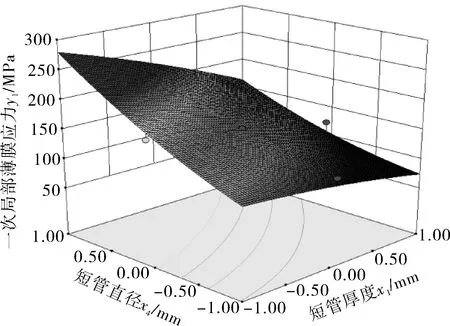
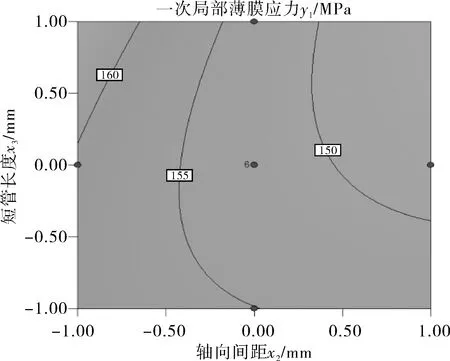

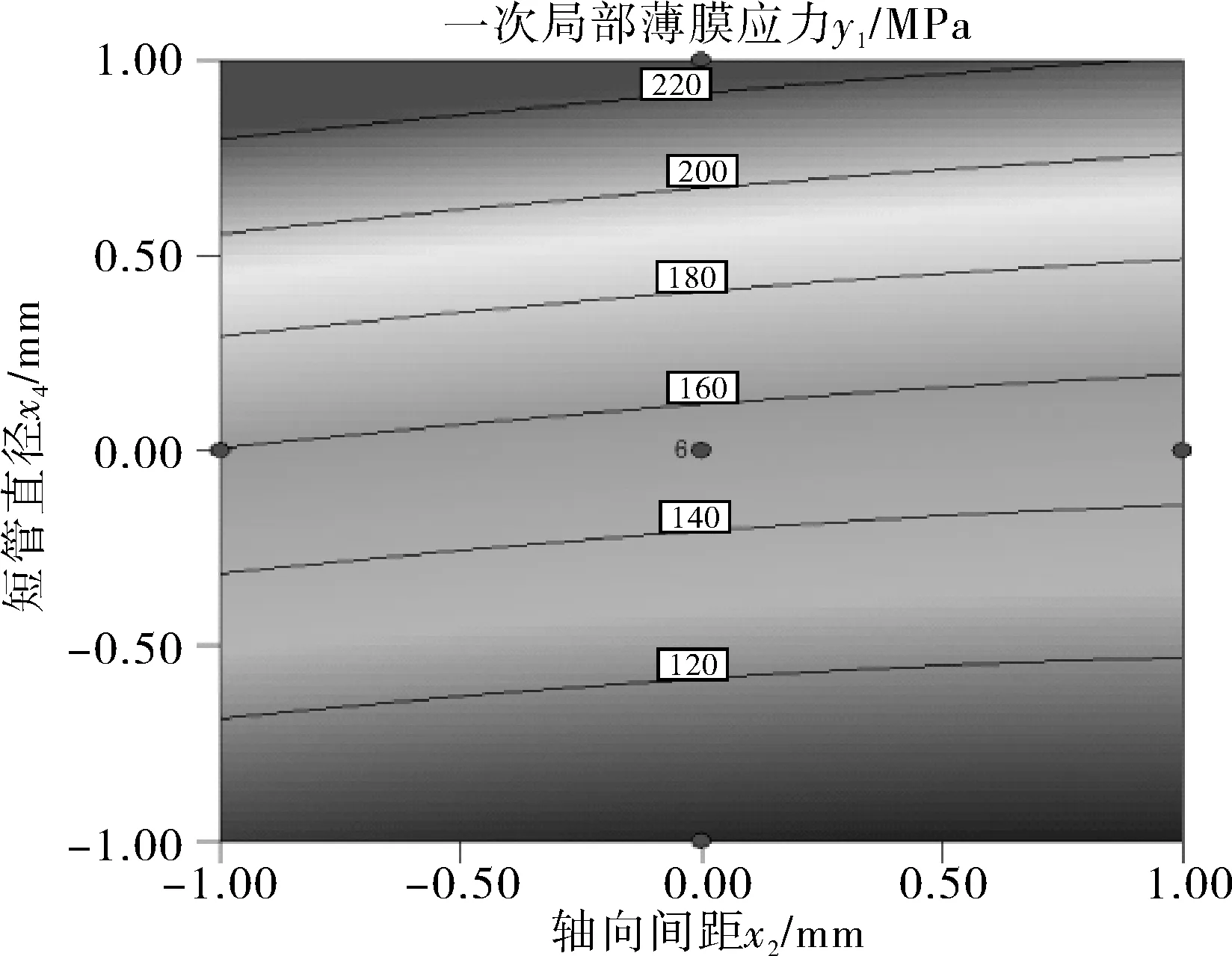
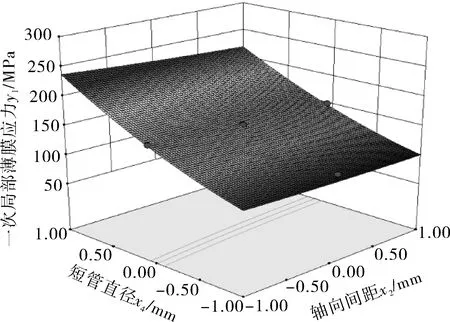


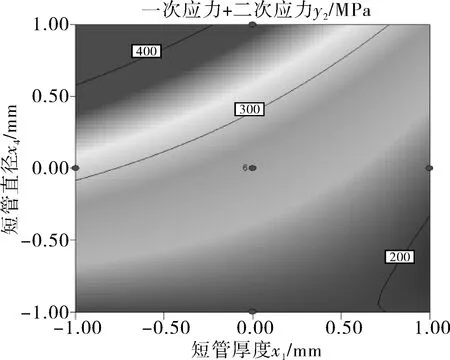


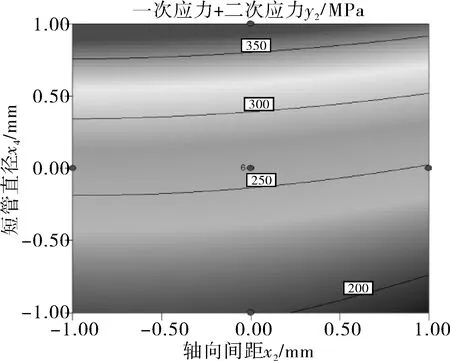



4 结语

