基于薄壳理论的焊接金属波纹管失弹机理研究

马咏梅， 卢翔宇，马传鑫，项章特，吴 昊，张 弦

(1.四川大学制造科学与工程学院，四川 成都 610065；2.四川日机密封件股份有限公司，四川 成都 610045；3.中国核动力研究设计院 核反应堆系统设计技术重点实验室，四川 成都 610213)

符 号 说 明

φ——子午线法线方向与对称轴之间的夹角，rad

a——环壳上某一点的截面半径，mm

r——环壳上某一点到轴线的距离，mm

ω——波纹膜片上某一点的法向位移，mm

ν——波纹膜片上某一点的切向位移，mm

εφ——轴向应变

εθ——周向应变

εφ′——轴向应变率

εθ′——周向应变率

εe——弹性应变

εc——蠕变应变

δe′——波纹膜片弹性变形率

δc′——波纹膜片蠕变变形率

εij——波纹膜片内一点的应力张量

Sij——波纹膜片内一点的应力偏张量

εij′——空间蠕变率张量

σ——等效应力，MPa

Sx——轴向应力偏张量

Sy——周向应力偏张量

F——波纹管弹力，N

焊接金属波纹管在机械密封中有着广泛的应用，其主要部件波纹膜片由薄板冲制而成。波纹膜片具有3段圆弧，不同膜片之间沿金属管内外边缘两两相切交替焊接在金属管上。焊接金属波纹管及波纹膜片焊接形式见图1。

图1 焊接金属波纹管及波纹膜片焊接形式示图

焊接金属波纹管会随着使用时间的延续而失弹，即弹性慢慢减小，这会引起焊接金属波纹管密封端面摩擦副之间闭合力的减小，严重时还会使密封失效，影响波纹管工作的可靠性，失弹因此成为波纹管研究的重要方向之一。WV Adams[1]研究了热油泵在高温下的密封失效，邱智杰[2]采用试验的方法研究了温度、载荷等因素对波纹管失弹的影响，文献[3-5]根据金属的蠕变理论对材料的应力松弛特性进行了研究，文献[6-7]用正交异形板理论近似推导出了焊接金属波纹管的失弹公式。这些研究存在的不足之处主要是，①未对焊接波纹管在工况下进行失弹试验。②采用正交异形板理论对波纹膜片方程作近似处理，未真实反映膜片结构与内力素间的本构关系。③运用正交异形板理论计算出的波纹管弹力值不够准确。

文中依据弹性薄壳理论，结合材料的应力松弛理论，导出了机械密封用焊接金属波纹管在实际工况下的失弹方程，采用薄壳理论解决了使用近似理论所得出计算结果不准确问题，得到了焊接金属波纹管的失弹曲线，并将有限元分析与理论计算结果进行对比，对基于薄壳理论建立的失弹方程进行了验证。

1 焊接金属波纹管失弹方程推导

1.1 薄壳理论中的应变位移关系[8-9]

根据薄壳理论建立环壳坐标尺寸，见图2。图2中，O为圆心，设点P为环壳上任意一点，点P到轴线的距离为r，P′为变形后P的位置，环壳的截面半径为a，整体半径为R，环壳上任意点P处的外法线和轴线的夹角为φ。

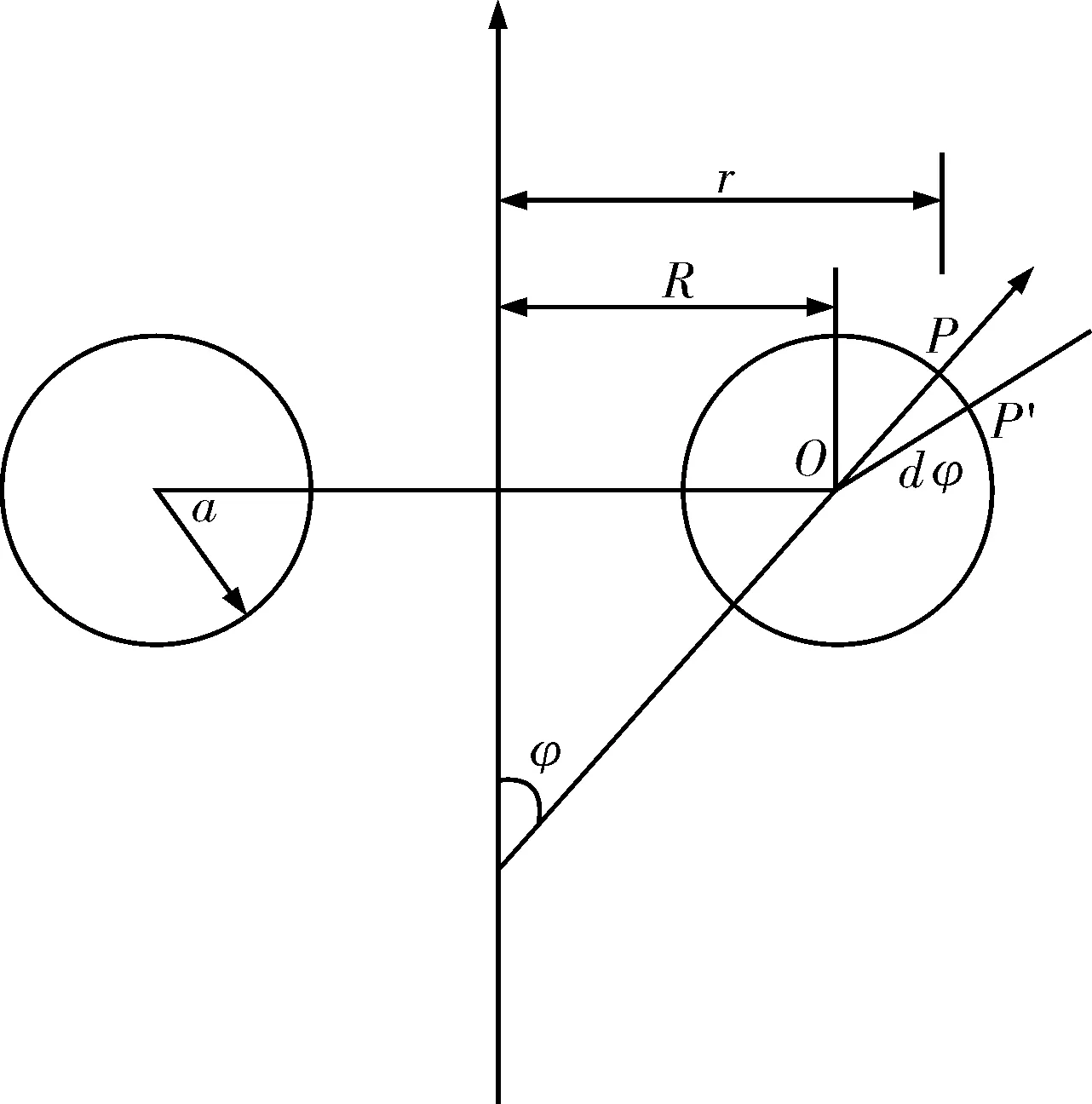
图2 环壳坐标尺寸

建立环壳的位移转角变形见图3。图3中，x为变形转角，y和z分别是点P的轴向位移和径向位移，ω和ν分别是点P的法向和切向位移，χ是点P的变形转角。

图3 环壳位移转角变形

壳体中的应变位移关系为：

(1)

(2)

由式(1)～式(2)得到壳体法向位移ω与应变εφ、εθ及角度φ之间的关系式：

(3)

式中的常数C由初始状态下的边界条件求出。

1.2 波纹管受力变形分析

假设波纹管压缩总变形为δ，弹性变形为δe，塑性变形为δp，蠕变变形为δc，则有：

δ=δe+δp+δc

(4)

假设工况中总压缩变形δ保持不变，在总压缩变形固定后，膜片不再产生塑性变形。将式(4)对时间t求导得：

δe′+δc′=0

(5)

(6)

将式(3)带入式(6)，得到：

(7)

式中，εφ′与εθ′都是关于初始应力、工作温度及时间的函数。

1.3 空间中的蠕变变形[10-12]

根据弹性力学，膜片体内一点应力状态可用9个应力分量表示如下：

(8)

膜片受力中，δx、δy、δz分别为轴向应力、周向应力与剪力。由式(8)得到应力偏张量：

(9)

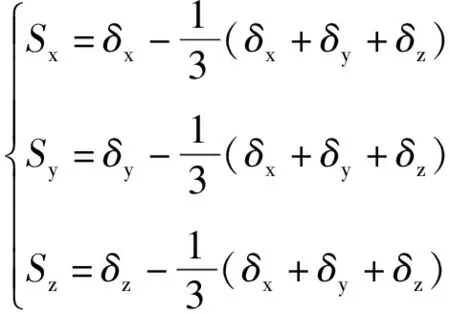
空间蠕变率张量：

(10)

(11)

(12)

1.4 波纹管失弹方程[13]

将式(11)、式(12)带入式(7)，可将弹力F表示如下：

(13)

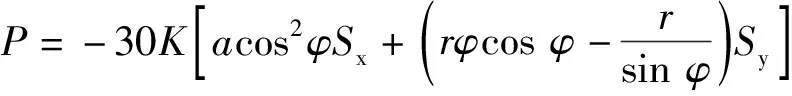
式中，F0为初始弹力，N。薄壳理论中δx、δy、δz、r均为角度φ的函数，对于给定圆弧的结构尺寸，可精确计算出系数P关于角度φ的数值解。

2 焊接金属波纹管失弹方程求解

2.1 确定膜片材料应力松弛参数

波纹管膜片材料应力松弛指膜片材料的应变保持不变情况下应力随时间的延续而减小的现象。一般认为，高温下材料的应力松弛与蠕变现象本质相同。根据材料应力松弛理论，膜片总应变ε0保持不变，弹性应变εe逐渐转变为蠕变应变εc，这种关系用计算式表达为：

ε0=εe+εc=常数

(14)

根据陈化理论，蠕变应变εc表示为：

εc=Aσntm

(15)

式中，A、m、n由膜片材料应力松弛试验得到。由式(14)、式(15)及材料的应力-应变关系，得到：

(16)

式中，E为弹性模量，MPa。根据式(16)，进一步推导得剩余应力σ与初始应力σ0和时间的关系式：

σ1-n=σ01-n+(n-1)EAtm

(17)

550 ℃时试验得到的膜片材料应力松弛曲线见图4[14-15]。

图4 550 ℃下膜片材料应力松弛曲线

从图4可知，波纹管膜片材料应力松弛曲线分为2个阶段，第1阶段持续时间较短，应力随时间延续而急剧下降；第2阶段持续时间很长，应力随时间延续而缓慢减小，并趋向恒定值。用MATLAB对试验数据进行曲线拟合，得到550 ℃下式(17)参数值A=2.241 6×e-8(e为自然常数)，m=0.027 23，n=1.696 1。

2.2 实际工况下波纹管应力松弛与失弹曲线

波纹管工况：温度550 ℃，波纹管弹力90 N，介质压力1 MPa。波纹管的尺寸参数：外径R1=45 mm，内径R2=40 mm，波形第一段圆弧半径a1=1.5 mm、波形第二段圆弧半径a2=1.4 mm、波形第三段圆弧半径a3=1.4 mm。

依据文献[13]给出的应力计算方法，将波纹管工况、尺寸参数带入MATLAB编程求解，得到初始应力σ0=648.7 MPa，由初始应力σ0及试验曲线拟合得到的A、m、n值做实际工况下波纹管的理论应力松弛曲线，见图5。

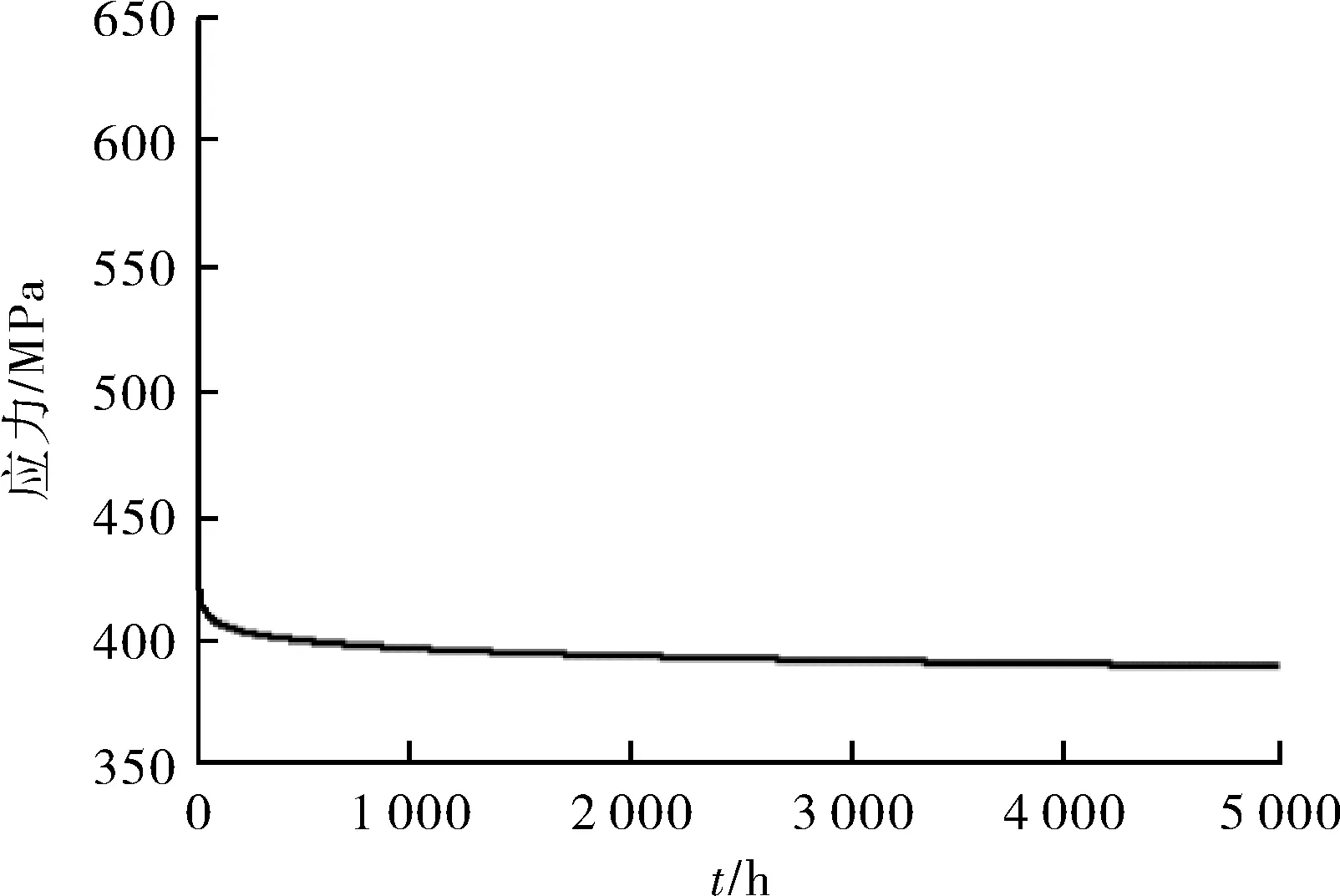
图5 实际工况下波纹管应力松弛曲线

从图5可以看出，经过5 000 h后，应力由648.7 MPa减小到388.13 MPa，减小了40.2%。将A、m、n带入(13)式中计算弹力F，得到波纹管失弹曲线，见图6。

图6 实际工况下波纹管失弹曲线

从图6可以看出，经过5 000 h后，波纹管弹力由90 N减小到81.14 N，弹力减小了9.8%。

3 波纹管失弹有限元分析

使用ANSYS Workbench的[Creep]蠕变模块对波纹管失弹进行有限元分析，并与理论计算结果比较。焊接金属波纹管的几何结构、载荷和边界条件都具有轴对称性，故在ANSYS Workbench中取波纹管单个波片的轴对称截面进行分析，以加快分析速度，提高分析结果的准确度。

3.1 前处理

在材料库[Engineering Data]添加波纹管材料Inconel-718，设置材料的弹性模量为2×1011MPa，泊松比为0.3，密度为824 0 kg/m3，在[Creep]选项中设置材料的3个蠕变常数[Creep Constant]分别为参数A、m、n的值。分析类型设置为2D轴对称模型，采用自动划分网格方法划分网格，插入[Face Sizing]与[Refinement]，细化波片网格。划分完成后的膜片网格见图7。

图7 波纹管膜片网格划分

3.2 求解设置

在ANSYS Workbench 中将膜片边界条件设定为：膜片外缘固定，内缘90 N弹力载荷等效转换为竖直方向位移约束0.06 mm，膜片外表面施加大小为1 MPa 压强，方向垂直于外表面。将求解载荷步设置为2步，以便于观察膜片在5 000 h 后的应力松弛结果。

3.3 求解结果

膜片最大等效应力分析云图见图8，膜片支承端的弹力变化分析云图见图9。

图8 波纹管膜片等效应力变化结果

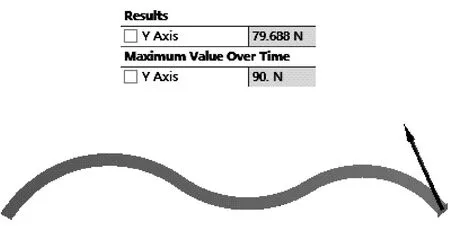
图9 波纹管膜片弹力变化结果

由图8可知，经过5 000 h的使用后，膜片最大等效应力由623.8 MPa减小为360.02 MPa，减小了42.3%。由图9可知，经过5 000 h的使用后，膜片轴向弹力由90 N减小为79.688 N，减小了11.5%。

4 有限元模拟与理论计算结果对比分析

4.1 应力变化

在MATLAB中得到的波纹管膜片理论计算与有限元分析的等效应力变化曲线见图10。

图10 波纹管膜片应力-时间变化曲线

从图10可以知道，理论计算的初始应力为648.7 MPa，最终应力为388.13 MPa，应力值变化了40.2%；有限元分析的初始应力为623.8 MPa，最终应力为360.02 MPa，应力值变化了42.3%。初始应力理论计算值与有限元分析值的误差为3.8%，最终应力理论计算值与有限元分析值的误差为7.2%，应力变化理论计算值与有限元分析值的误差为2.1%。

4.2 弹力变化

在MATLAB中得到的波纹管膜片理论计算与有限元分析的等效弹力变化曲线见图11。

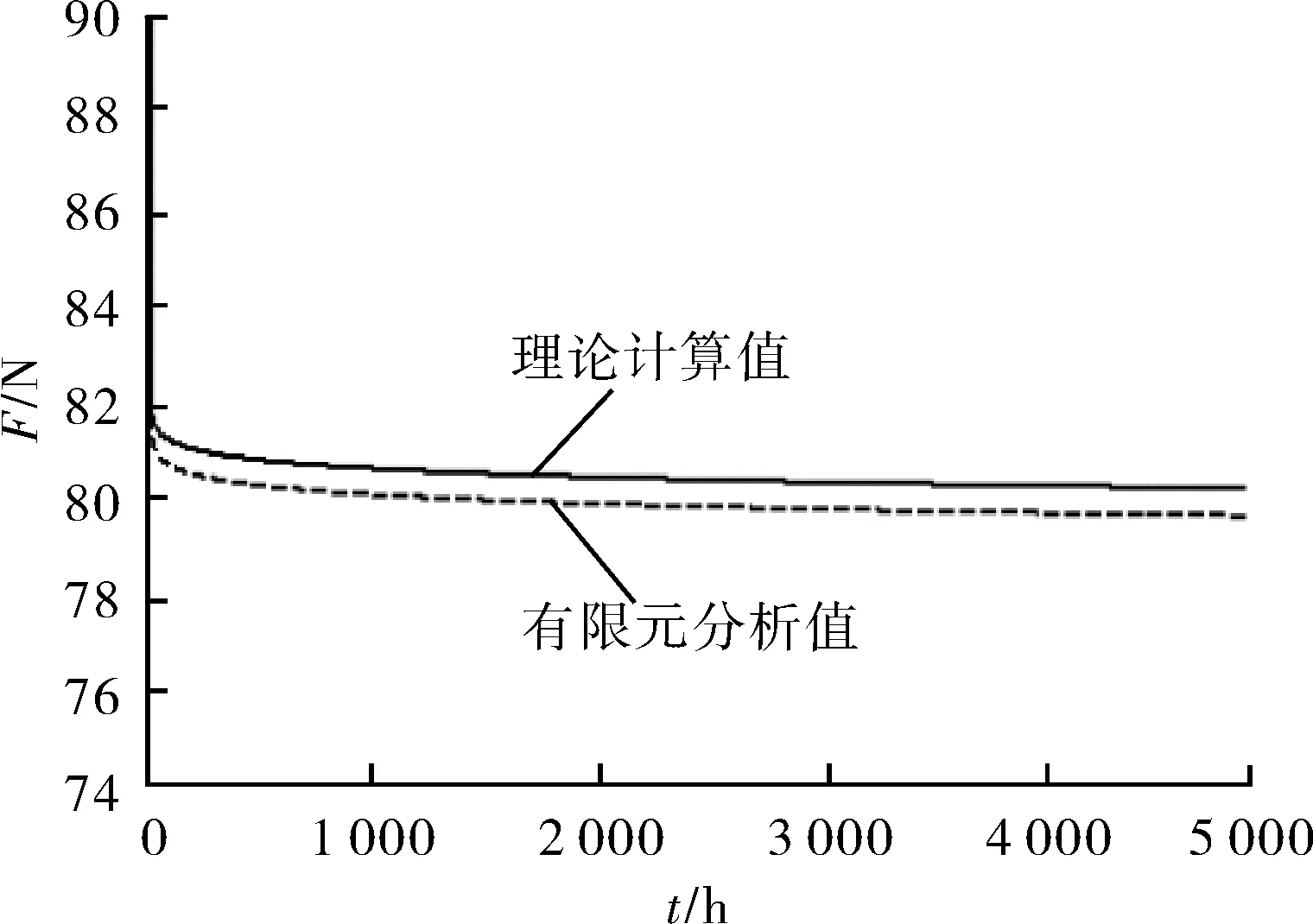
图11 波纹管膜片弹力-时间变化曲线

从图11可知，理论计算初始弹力为90 N，最终弹力为81.14 N，弹力值变化了9.8%；有限元分析的初始弹力为90 N，最终弹力为79.69 N，弹力值变化了11.5%。初始弹力理论计算值与有限元分析值的误差为0%，最终弹力理论计算值与有限元分析值的误差为1.8%，弹力变化理论计算值与有限元分析值的误差为1.7%。

4.3 综合分析

理论计算与有限元分析的应力和弹力变化分析一致表明，在误差允许范围内理论计算与有限元分析结果吻合较好，理论计算公式能较好地描述波纹管长期在高温下工作的失弹现象，有限元分析验证了理论计算的正确性。针对理论计算与有限元分析产生的误差进行分析，认为主要为2个方面的原因所致，①运用轴对称细环壳一般解的方法求解方程时，对部分数据处理时忽略了少数微小量。②有限元分析中，部分选项设置，如网格划分大小、单元类型的选择等对分析结果影响较大。

5 结论

(1)依据弹性薄壳理论建立了焊接金属波纹管在实际工况下的失弹方程，该方程能较好地反映波纹管的失弹情况。

(2)影响波纹管失弹的因素有波纹管的初始应力、刚度、工作温度以及在高温下工作的时间。

(3)波纹管的初始应力与波纹管自身结构有关，因此，对波纹管进行结构优化设计时，在给定工况下，应该以减小初始应力为目标优化波纹管结构，可减轻波纹管的失弹现象。

(4)在一定范围内，波纹管刚度值越大、工作温度越高，波纹管失弹现象越明显。

(5)波纹管在高温下工作的时间越长，波纹管失弹现象越明显。因此，在外界条件不变的情况下，应根据理论计算数据，合理安排波纹管使用时间，避免失弹使密封失效。