存在内表面轴向裂纹压力容器的模态分析
,,,,
(1.上海蓝滨石化设备有限责任公司,上海 201518;2.中国石油 独山子石化分公司,新疆 克拉玛依 833699;3.中国石油 乌鲁木齐石化分公司,新疆 乌鲁木齐 830019)
冶炼过程中产生位错及微裂纹的材料加工成容器时,容器表面可能会出现裂纹,此种容器在焊接制造中也会产生裂纹,使得压力容器或多或少都带有缺陷[1-2]。宏观或微观裂纹的存在都可能引起压力容器结构部分开裂或整体破坏,成为导致压力容器事故的根源[3-4]。石油与天然气化工领域中服役的压力容器大都处于高温、高压、强腐蚀等极端工作环境,不仅有静载荷的影响,还会受到温度变化、压力变化甚至地震等动载荷的影响,这些都是诱发和增大压力容器事故灾难概率的重要因素[5-6]。
前人已对压力容器裂纹及其影响做过大量的相关研究。晓风清等[7]在研究奥氏体不锈钢制深冷容器应变强化规律时,利用有限元模拟与分析建立了容器的整体模型,并找出其最大应力位置。孙志明等[8]在设计大型卧式真空容器时,采用有限元软件ANSYS进行计算分析,得到了真空容器工作时的应力及变形分布,并采用优化结构代替了传统工艺,得到了更稳定的真空容器。赵磊等[9]在拉弯联合载荷作用下,对带有半椭圆形表面裂纹的平板模型进行概率断裂力学分析,得到了处于拉弯联合载荷作用时该平板模型裂纹尖端的应力强度因子和J积分值。祁建磊等[10]利用ANSYS分析得出带有2条平行裂纹的在役球形罐体在其裂纹合并前后的疲劳寿命,通过仿真分析得到了不同间距平行裂纹对罐体的影响,描绘出裂纹尖端应力强度因子和裂纹间距的关系图谱。陈孙艺[11]对某些压力容器的简化模型在有限元分析中引起的结果误差,以及建立这类模型对其他案例产生的误导情况进行了综述,并从技术背景、设备结构、运行工艺等方面强调了建模的注意事项,通过案例分析提出模型的优选方案。文中利用有限元软件ANSYS Workbench建立模型,从自振频率角度分析不同深度和位置的裂纹对压力容器安全性的影响。
1 两端固定压力容器自振频率ANSYS模拟
1.1 无裂纹压力容器
构建无裂纹奥氏体不锈钢0Cr21Ni6Mn9N压力容器模型[12],见图1。

图1 无裂纹压力容器自振频率ANSYS分析模型
压力容器材料弹性模量为193 GPa,泊松比为0.302,密度为7.93 g/cm3,筒体外直径42 mm,内直径35 mm,筒壁厚度7 mm。
把图1压力容器模型的两端固定住,在ANSYS Workbench中进行模态分析,得到的前10阶自振频率见表1[13]。

表1 两端固定有无裂纹压力容器前10阶自振频率
1.2 存在内表面轴向裂纹压力容器
在图1压力容器模型上假设存在1条内表面轴向裂纹,见图2。图中a为裂纹深度,c为裂纹长度,c=5a。裂纹沿其深度方向的有效厚度为δ,a=0.1δ。

图2 存在内表面轴向裂纹压力容器自振频率ANSYS分析模型
把图2中压力容器的两端头固定,沿y轴正方向施加80g(g为重力加速度)惯性力和40 MPa内压,进行有限元法静力分析得到的米塞斯应力云图见图3。从图3可知,内表面轴向裂纹尖端区域存在应力集中,说明该位置的应力最大。

图3 存在内表面轴向裂纹压力容器米塞斯应力云图
模态分析后得出的存在内表面轴向裂纹压力容器前10阶自振频率见表1。对比表1中的自振频率数据可以发现,内表面轴向裂纹的存在对于压力容器前7阶的自振频率无明显影响,明显的变化主要发生在第8和第9阶自振频率上,存在内表面轴向裂纹压力容器比无裂纹压力容器的自振频率分别下降了8.04%和9.08%。
2 两端自由圆筒自振频率ANSYS模拟
2.1 圆筒建模
以压力容器的筒体部分为研究对象,根据其相似性可以推断,由图1和图2模型得到的振型极有可能也反映了对应状态下压力容器筒体部分的振型情况[14]。建立无裂纹和存在内表面轴向裂纹圆筒的2种有限元模型(图4),进一步探究图1和图2模型振型与压力容器筒体部分振型的相关性。
图4 圆筒自振频率ANSYS分析模型
2.2 模态分析
假设圆筒的两端呈自由约束状态,使用ANSYS软件分别对图4a和图4b中圆筒模型进行模态分析,得到2种圆筒前10阶的自振频率,见表2。
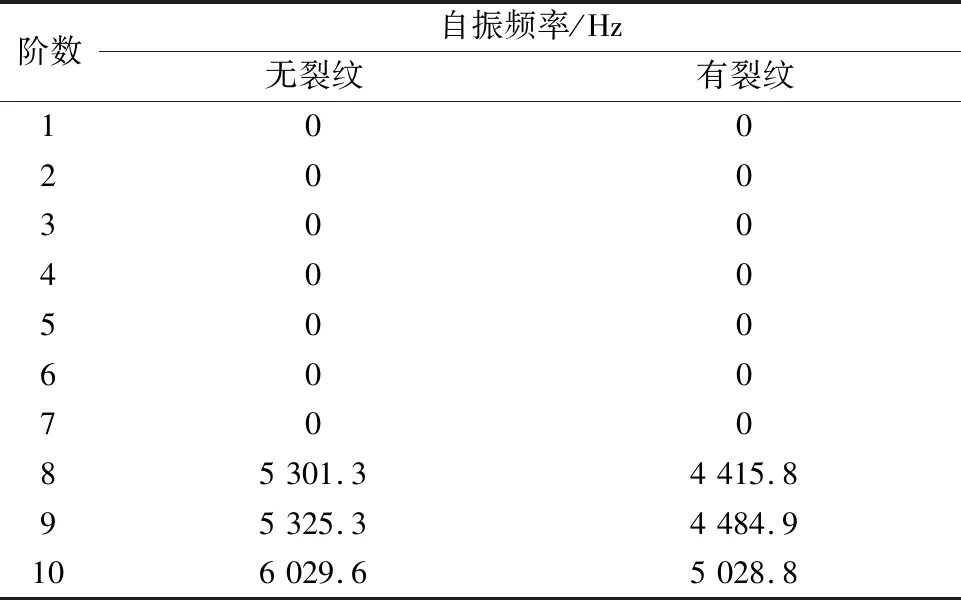
表2 有无裂纹圆筒前10阶自振频率
表2显示,圆筒前7阶自振频率均为0,这说明自由约束状态下圆筒前7个模态都属于刚体运动,从第8阶开始筒体部分才发生振动。
对比表2中无裂纹圆筒与有裂纹圆筒的自振频率可以知道,自第8阶开始,有裂纹圆筒的自振频率明显较小,说明内表面轴向裂纹的存在使得筒体结构的自振频率减小,其在宏观上的反映是降低了筒体结构的可靠性。
2.3 振型图分析
无裂纹圆筒的第8、9阶振型图见图5,压力容器的第8、9 阶振型图见图6。

图5 无裂纹圆筒的第8阶和第9阶振型图
综合文中得到的自振频率数据分析图5、图6可知,无裂纹圆筒与无裂纹压力容器的第8、第9阶的自振频率差别不大。无裂纹圆筒第8、第9 阶的自振频率较低,是因为图4a中的模型无任何约束,与图1模型相比其筒体部分更为自由。图1模型的第8、第9阶振型能够真实反映压力容器筒体部分的振型情况。要探究内表面轴向裂纹对压力容器筒体部分自振频率的影响,仅需研究图1、图2模型的第8、第9 阶的振动情况即可。

图6 无裂纹压力容器第8和第9阶振型图
3 裂纹对压力容器自振频率的影响
3.1 裂纹相对深度
3.1.1总体规律
内表面轴向裂纹相对深度a/δ的变化会对结构的自振频率产生影响,进而影响筒体结构的可靠性[15]。通过计算a/δ为0.1、0.3、0.5时压力容器的自振频率,来探究内表面轴向裂纹相对深度对压力容器自振频率的影响情况,结果见表3。
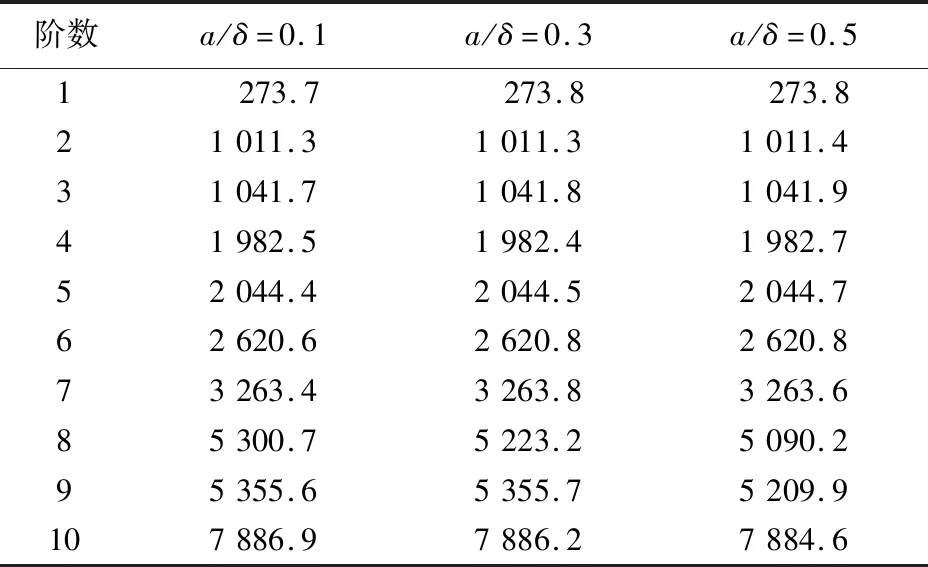
表3 不同裂纹深度压力容器前10阶自振频率 Hz
由表3可知,内表面轴向裂纹深度仅对第8和第9阶自振频率有显著影响。由此可推断,筒体内表面轴向裂纹相对深度的变化对压力容器整体结构自振频率的影响较小,只对筒体的影响较显著。
3.1.2显著规律
使用表3中数据作图研究第8、第9阶自振频率随a/δ的变化规律,见图7。

图7 压力容器第8和第9阶自振频率随a/δ变化规律
由图7可知,当压力容器筒体部分含有内表面轴向裂纹时的,第8、第9 阶自振频率全都小于无裂纹时的。当a/δ为0.1~0.5时,随着相对深度的增加,压力容器的自振频率反而减小。分析认为,这是因裂纹相对深度的增加导致了结构整体刚度的降低,其自振频率也随之减小。
3.2 裂纹位置
3.2.1总体规律
裂纹位置变化时,结构的自振频率可能会随之不同[16]。压力容器模型上裂纹位置见图8。图中,L表示压力容器筒体部分的总长度,l表示内表面轴向裂纹至筒体右端的长度。

图8 压力容器裂纹位置示图
计算l/L为1/2、1/3、1/6 时压力容器前10阶自振频率,探究内表面轴向裂纹相对位置对压力容器自振频率的影响情况,结果见表4。
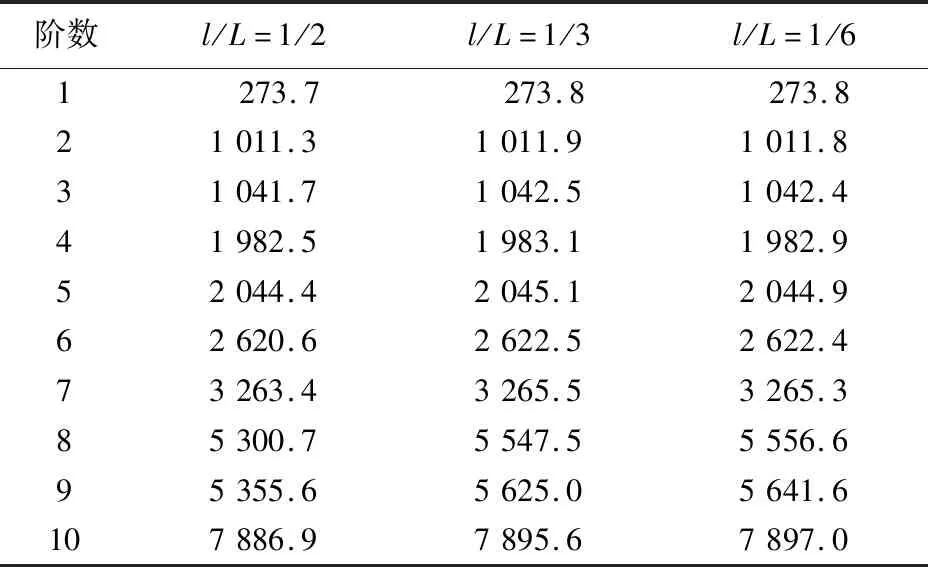
表4 不同裂纹位置的压力容器前10阶自振频率 Hz
由表4可知,内表面轴向裂纹所处位置仅对第8、第9阶的自振频率有显著影响。由此可推断,筒体内表面轴向裂纹所处位置变化值对结构的自振频率影响情况和相对深度的影响情况结论一致,都是对压力容器整体结构自振频率的影响较小,只是对筒体部分的影响较为显著。
3.2.2显著规律
使用表4中数据作图研究第8、第9阶自振频率随裂纹相对位置的变化规律,见图9。

图9 压力容器第8和第9阶自振频率随裂纹位置变化规律
从图9可以看出,0随l/L的增大,第8、第9阶自振频率反而减小,即裂纹所处的位置越靠近筒体中间时,其自振频率越小,越不稳定。因此,为保证压力容器在实际工程应用时的安全可靠性,务必重视筒体中间位置附近内表面轴向裂纹的检测。
4 结语
利用有限元软件ANSYS Workbench分别建立了无裂纹和存在内表面轴向裂纹压力容器的有限元模型,通过模态分析分别得出其前10阶自振频率,计算出裂纹处于压力容器筒体不同深度和位置时对应的自振频率,并探究了第8、第9阶自振频率随a/δ和裂纹位置变化的规律,得到以下结论:①压力容器模型的第8、第9阶振型能够真实反映压力容器筒体部分的振型情况。②筒体内表面轴向裂纹相对深度和所处位置变化值对结构的自振频率影响情况一致,都是对压力容器整体结构自振频率的影响较小,只是对筒体部分的影响较为显著。③压力容器的自振频率随着裂纹相对深度的增加而减小。其原因是裂纹相对深度的增加导致了结构整体刚度的降低,因此其自振频率也随之减小。④裂纹所处的位置越靠近筒体中间时,其自振频率越小,越不稳定。为保证压力容器在实际工程应用时的安全可靠性,务必重视筒体中间位置附近内表面轴向裂纹的检测。

