基于焦点弦的一道预赛题最值问题探究*
湖北恩施州教育科学研究院(445000) 周 威
对预赛试题的探究与迁移,有助于提升学生的思维高度、开阔学生的数学视野,而非仅仅停留在“解题”的表面,既为开展研究性学习和数学探究活动提供素材,也为核心素养的落实提供可行的途径.
一、试题呈现与问题提出
例(2019年新疆预赛试题)设F是椭圆E:+y2=1 的左焦点,过点F斜率为正的直线l与E相交于A,B两点,过点A,B分别做直线AM和BN满足AM⊥l,BN⊥l,且直线AM,BN分别与x轴相交于M和N,试求|MN|的最小值.
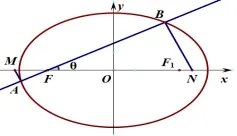
图1
解如图1,设直线l的倾斜角为在RtΔMAF中有|MF|=在RtΔNBF中有|NF|=所以|MN|=|MF|+|FN|=设F1是椭圆的右焦点,连接BF1,记|BF|=x,则|BF1|=−x.由余弦定理得|BF1|2=|BF|2+|FF1|2−2|BF||FF1|cosθ,即有|BF|=x=
同理可得|AF|=所以|AB|=|AF|+|BF|=所以|MN|=令f(θ)=(3−2cos2θ)2·4 cos2θ,则由均值不等式有

当且仅当3−2cos2θ=4 cos2θ取等号,即θ=时f(θ)max=4,此时|MN|min=
题中|AB|其实就是焦点弦,问题背景十分熟悉,解答过程也很自然.过焦点的直线与椭圆相交于两点,让人很自然到想到过焦点的弦长公式,从而转换到|AB|与|MN|的关系上来.值得一提的是在求f(θ)max时,还可以利用函数导数进行求解.
问题2|MN|的最值问题是否可以类比迁移到双曲线和抛物线的情形? |MN|的最小值是否存在?
二、基于焦点弦的等式关系探究
通过上述问题导向,不难发现,问题1 中对于|AB|与|MN|的关系有如下性质:
性质1设F是圆锥曲线E的一个焦点,过点F的直线l倾斜角为直线l与E相交于A,B两点,过点A,B分别做直线AM和BN满足AM⊥l,BN⊥l,且直线AM,BN分别与x轴相交于M和N.则当θ∈(0,)时,|MN|=当时,

图2
证明先考虑椭圆情形,当直线l的倾斜角为时,由图1,显然|MN|=当直线l的倾斜角为时,如图2,在RtΔMAF与RtΔNBF中,始终满足cos(π −θ)=所以|MN|=|MF|+|FN|=
当圆锥曲线为双曲线或抛物线时,分别如图3、图4,显然也满足.
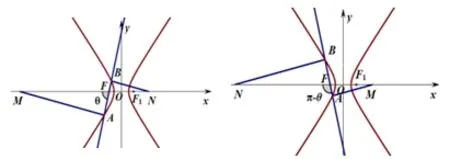
图3 (直线l 的斜率分别为正、负的情形)

图4 (直线l 的斜率分别为正、负的情形)
我们知道,其实圆锥曲线焦点弦|AB|的弦长有如下性质:
性质2直线l过椭圆E:=1(a >b >0)的一个焦点F(±c,0),且l的倾斜角为θ,与椭圆相交于A,B两点,则|AB|=
性质3直线l过双曲线E:=1(a >0,b >0)的一个焦点F(±c,0),且l的倾斜角为θ,与双曲线相交于A,B两点,则|AB|=
性质4直线l过抛物线E:y2=2px(p >0)的焦点F,且l的倾斜角为θ,与抛物线相交于A,B两点则
(3)区内一六、梅子冲典型矿床深部有较好的找矿空间。其中一六钨矿区在黑云母花岗岩的凹凸部位、层间滑脱面及多组构造的交汇部位是成矿最为有利的地段;梅子冲银铅锌矿区的隐爆角砾岩与成矿关系密切,在其与隐伏岩体和沉积岩地层的接触带、构造虚脱部位有望寻找到中大型岩浆热液型多金属矿床。
性质2-4 限于篇幅,请读者自己完成证明.
三、最值问题推广与结论
基于以上四条性质,可以将圆锥曲线情境下的|MN|最值结论作如下推广:
结论1设F是椭圆E:=1(a >b >0)的一个焦点,过点F的直线l与E相交于A,B两点,过点A,B分别做直线AM和BN满足AM⊥l,BN⊥l,且直线AM,BN分别与x轴相交于M和N.当离心率e >时,|MN|才存在最小值且|MN|min=
证明当直线l的斜率为正时,设其倾斜角为θ(0<θ <),结合性质1、性质2 及b2=a2−c2,有|MN|=令t=cosθ∈(0,1),则(a2−c2cos2θ)cosθ=(a2−c2t2)t,令f(t)=(a2−c2t2)t,则f′(t)=a2−3c2t2,当f′(t)=0 时,t=(e为离心率),由函数单调性可知,当<1 时,即e >时,f(t)在上单调递增,在上单调递减,f(t)存在最大值f(t)max==当时,即0<e≤时,f(t)在(0,1)上单调递增,无最大值.因此,只有e >时f(t)才存在最大值此时|MN|min=
同理可证直线l的斜率为负的情形.
对于问题2,首先看双曲线的情形.事实上,过双曲线焦点的直线与双曲线相交时,会有两种情况: 一种是A,B两点同为双曲线左(右)支上的点,如图3,此时由性质3及c2=a2+b2知|AB|=一种是A,B两点分别在双曲线不同两支上,如图5,此时由相性质3 知|AB|=

图5
因此,可得以下结论:
结论2设F是双曲线E:=1(a >0,b >0)的一个焦点,过点F的直线l与E相交于A,B两点,过点A,B分别做直线AM和BN满足AM⊥l,BN⊥l,且直线AM,BN分别与x轴相交于M和N.当A,B两点位于双曲线同支时,|MN|才存在最小值且|MN|min=
证明当直线l斜率为正,设其倾斜角为θ(0<不妨设F是双曲线的左焦点,当A,B两点位于双曲线左支时,如图3,|AB|=此时a −ccosθ >0,即cosθ <由性质1,|MN|=所以|MN|=令t=cosθ∈(0,),则(a2−c2cos2θ)cosθ=(a2−c2t2)t,令f(t)=(a2−c2t2)t,则f′(t)=a2−3c2t2,当f′(t)=0 时,t=由函数单调性可知,f(t)在上单调递增,在上单调递减,f(t)存在最大值f(t)max=此时|MN|min=
当A,B两点分别位于双曲线左、右两支时,如图5,|MN|=|FN| −|MF|=,|MN|=此时ccosθ −a >0,即cosθ >令t=cosθ∈则(c2cos2θ −a2)cosθ=(c2t2−a2)t,令f(t)=(c2t2−a2)t,则f′(t)=3c2t2−a2,当f′(t)=0时,故f(t)在上单调递增,无最大值,从而|MN|无最小值.
综上,只有当A,B两点位于双曲线左支时,f(t)才存在最大值,即|MN|min=同理可证直线l斜率为负或F为右焦点情形.
结论3设F是抛物线E:y2=2px(p >0)的焦点,过点F的直线l与E相交于A,B两点,过点A,B分别做直线AM和BN满足AM⊥l,BN⊥l,且直线AM,BN分别与x轴相交于M和N,那么|MN|min=
证明不妨设直线l斜率为正,则其倾斜角为θ(0<如图4,|MN|=|MF|+|FN|=由性质4得,|MN|=令t=cosθ∈(0,1),则sin2θcosθ=t −t3.令f(t)=t −t3,则f′(t)=1−3t2,当f′(t)=0 时,t=,f(t)在上单调递增,上单调递减.f(t)存在最大值f(t)max= 此时
同理可证直线l斜率为负的情形.

