高一函数与立体几何课堂学习行为的对比研究

吴慧 朱福胜

（1.集美大学理学院福建厦门361021；2.广东省饶平县钱东中学广东潮州515726）

一、问题的提出

高中阶段是人生数学学习的重要阶段。高中阶段数学教育应提升学生的数学素养，引导学生会用数学眼光观察世界，会用数学思维思考世界，会用数学语言表达世界。PISA也将阅读、数学与科学素养作为学生适应未来生活应具备的基本素养。［1］2019年，国务院办公厅《关于新时代推进普通高中育人方式改革的指导意见》中明确指出：“按照教学计划循序渐进开展教学，提高课堂教学效率，培养学生学习能力，促进学生系统掌握各学科基础知识、基本技能、基本方法，培养适应终身发展和社会发展需要的正确价值观念、必备品格和关键能力。”学生是学习的主体，课堂是学生学习的主要场所，课堂学习行为可以反映学生学习的主动性、思维方式和理解水平，不同模块的课堂学习行为的对比研究可以为教学改进指明方向、取长补短，追求课堂质量的最优化。

高一数学是高中数学的基础，高一数学知识占了高考总分的60%以上，函数与立体几何在高一数学中有着极其重要的地位，既是重点也是难点。就内容而言，函数是高中数学的一个核心知识，贯穿高中整个数学学习的始末，起着决定性的作用；立体几何也是高中数学经典且重要的内容，是学习空间向量的基础。“数学之所以在灵活性和重要性上远远超过那些依赖于它的科学，是因为它完全包括了这些科学的研究对象和许许多多的别的东西。”［2］基于较长时间的个人观察和感悟，通过与一线教师、教研员的交流，发现学生在从初中数学学习向高中数学学习的转变过程中，对于不同的数学课程内容，其课堂学习行为的表现是不同的。由此，笔者基于观察、记录、数据分析，探讨在高一函数和立体几何课堂上学生学习行为所表现出的规律、特点以及影响因素等。

二、数据的收集

（一）“高中数学课堂学生学习行为观察量表”的设计

根据学生在课堂表现的外显行为以及高中数学课堂固有的特点，我们把高中数学课堂学生学习行为分为四个一级维度，分别是倾听行为、言说行为、操作行为以及无效行为：倾听行为分为听教师、听学生；言说行为包括提问、回答、交流、评价；操作行为包括思维操作、记笔记、做习题；无效行为包括静默等待、发呆、做小动作、打瞌睡、闲聊等。课堂观察量表由两个层次构成，其中一级维度4个，分别定为A、B、C、D；二级维度有14个，分别定为A1、A2、B1、B2、B3、B4、C1、C2、C3、D1、D2、D3、D4、D5，如表1所示。

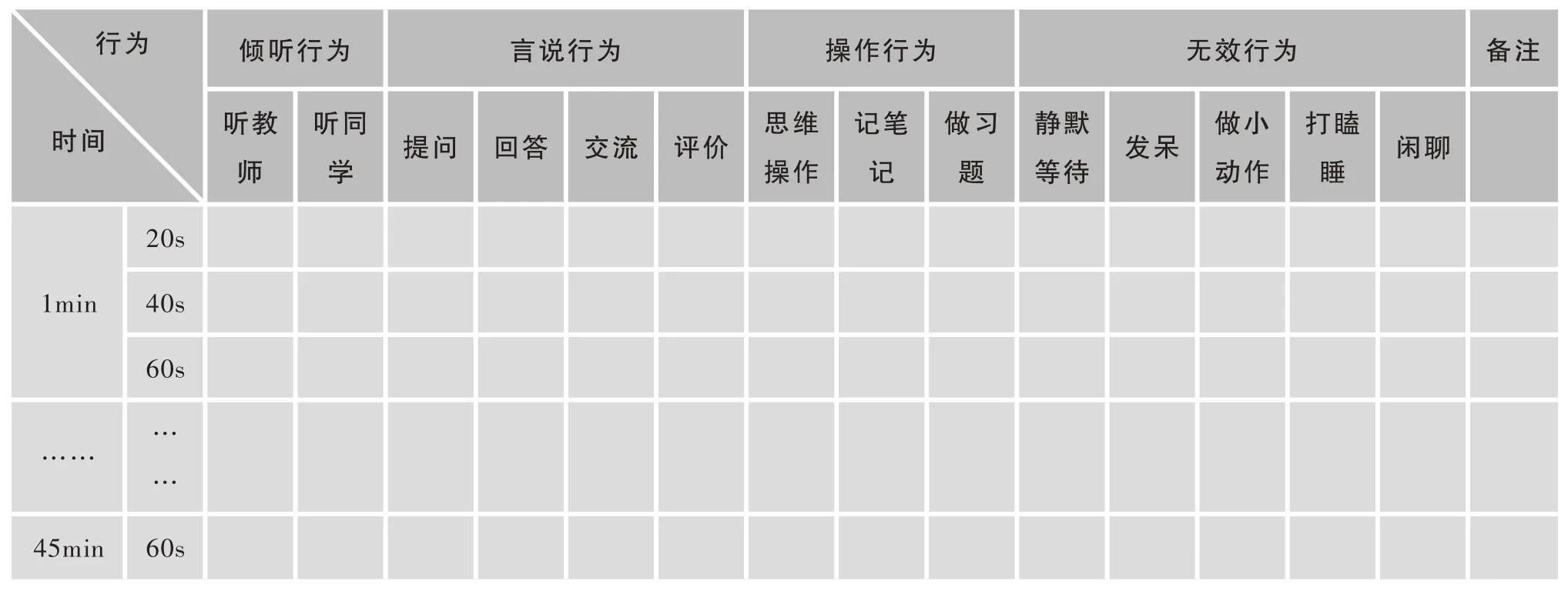
表1 高中数学课程学生学习行为观察量表

（二）“高中数学课堂学生学习行为观察量表”的信效度

本文的观察量表是在文献分析的基础上，结合高中数学课堂学生学习行为的外在表现设计的，并经过专家们的论证与修订，所以该观察量表具有较好的内容效度。然后请两位高中数学老师A、B分别用这份观察量表对函数单调性的课堂环节——例题讲解（第20分钟到第29分钟）的“听教师”“听同学”“思维操作”“静默等待”“发呆”这几个学习行为进行观察记录（这五种学习行为是最容易混淆的），然后运用SPSS 20.0中的Pearson相关性、Spearman的rho分析其相关关系。分析结果为：A和B教师的Pearson相关性是0.998、Spearman的rho相关系数是0.985，而它们的显著性值都是0.000，都小于0.01，所以它们有显著的相关性，据此评判该量表在使用中具有良好的信度。

（三）“高中数学课堂学生学习行为观察量表”的记录

研究对象是某完全中学高一（4）班全体学生，总人数53人。该完全中学的学生基础比较薄弱，入学的数学平均分约71分（满分120分）。授课老师是同一个人，具有近20年的一线教学经验。观察记录的两节课是函数的单调性和线面垂直的判定，主要采用的教学方法是讲授法。这两节课都是函数和立体几何内容的关键节点，要求有一定的知识储备，也是后续内容的基础。观察者首先在同一时间间隔里对各个学生的学习行为做出判定，然后统计各种学习行为的人数，接着填入编码系统的相应编码里，形成一个连续的数据记录表。表中每行表示每20秒的各种学习行为的数量，竖列表示一节课的时间为45分钟。课堂观察时先记录第一横行，再记录第二横行，依次类推，一节课会有1890个数字。

三、结果与分析

（一）两节课学习行为一级维度的对比分析

从学习行为人数统计量的平均值看，函数单调性和线面垂直判定这两节课的“倾听行为”均值分别是37.15和33.85，“言说行为”的均值分别是19.30和9.09，而“操作行为”的均值分别是13.78和16.48，“无效行为”的均值分别是11.64和20.07。接着，把学生学习行为各自对应作为两独立样本，通过Explorer过程检测数据是否服从正态分布。得到结果为，“倾听行为”“言说行为”“操作行为”和“无效行为”的Kolmogorov-Smirnovb和Shapiro-Wilk的统计量都是大于0.05，都符合正态分布。两者“倾听行为”的Kolmogorov-Smirnovb的统计量分别是0.188和0.186，而Shapiro-Wilk的 统 计 量 分 别 是0.851和0.894，如表2所示。

表2 正态性检验a

然后，进行两独立样本T检验，得到结果为，“倾听行为”的方差方程的Levene检验F统计量的值是2.300，对应的置信水平是0.131，说明两样本方差之间不存在显著差别，所以采用的方法是两样本等方差T检验。它对应t的统计量的值是2.020，自由度是161，95%的置信区间是（0.074，6.540），临界置信水平为0.045，小于5%。说明两节课的“倾听行为”有着明显的差异，如表3所示。

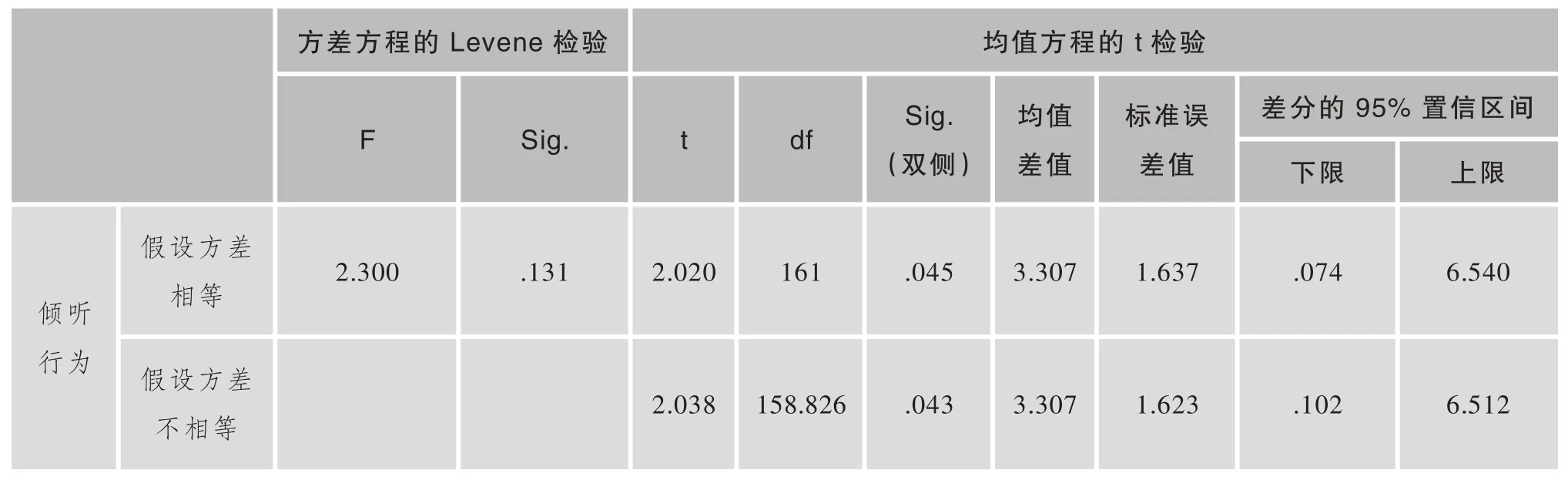
表3 独立样本检验

同理，可以得到，“言说行为”和“无效行为”的临界置信水平都是0.000，远小于5%，说明两节课的这些学习行为有显著的差异。而“操作行为”的临界置信水平是0.121，说明两节课的这一学习行为没有明显的差异。

（二）两节课学习行为二级维度的对比分析

总体来说，函数单调性课堂上有关学习行为的人数均值大多数都高于线面垂直判定的课堂有关学习行为，如“听教师”的均值分别是40.87和35.06，标准差是6.693和8.232，“回答”（群答）的均值分别是29.83和19.75。函数单调性课堂上无效行为低于线面垂直判定的课堂无效行为，如“静默等待”分别是368和886人次，“做小动作”的分别是476和637人 次。

二级维度的分析方法跟一级维度相同，得到结果为“听教师”“听同学”“提问”“回答”“交流”“评价”“思维操作”“记笔记”“做习题”“静默等待”“发呆”“做小动作”“打瞌睡”和“闲聊”等学习行为的Kolmogorov-Smirnovb和Shapiro-Wilk的统计量都是大于0.05，都符合正态分布。

两独立样本T检验得到结果为，“听教师”的方差方程的Levene检验F统计量的值是0.775，对应的置信水平是0.380，它对应t的统计量的值是4.360，自由度是125，95%的置信区间是（3.173，8.448），临界置信水平为0.000，远小于5%，这说明两节课的“听教师”这一学习行为有着明显的差异，如表4所示。

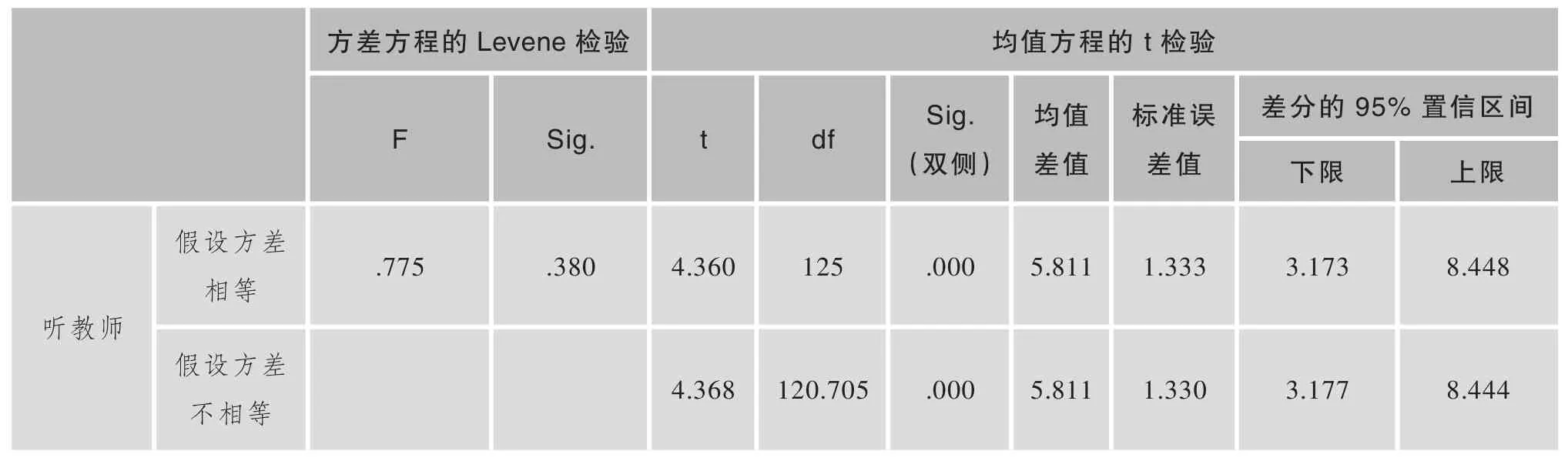
表4 独立样本检验

“听同学”的方差方程的Levene检验F统计量的值是5.939，对应的置信水平是0.020，小于0.050，说明两样本方差之间存在显著差别，所以采用的方法是两样本不相等方差T检验。它对应t的统计量的值是-0.395，自由度是32.252，95%的置信区间是（-10.991，7.420），临界置信水平为0.695.远大于5%。说明两节课的“听同学”这一学习行为没有明显的差异，如表5所示。

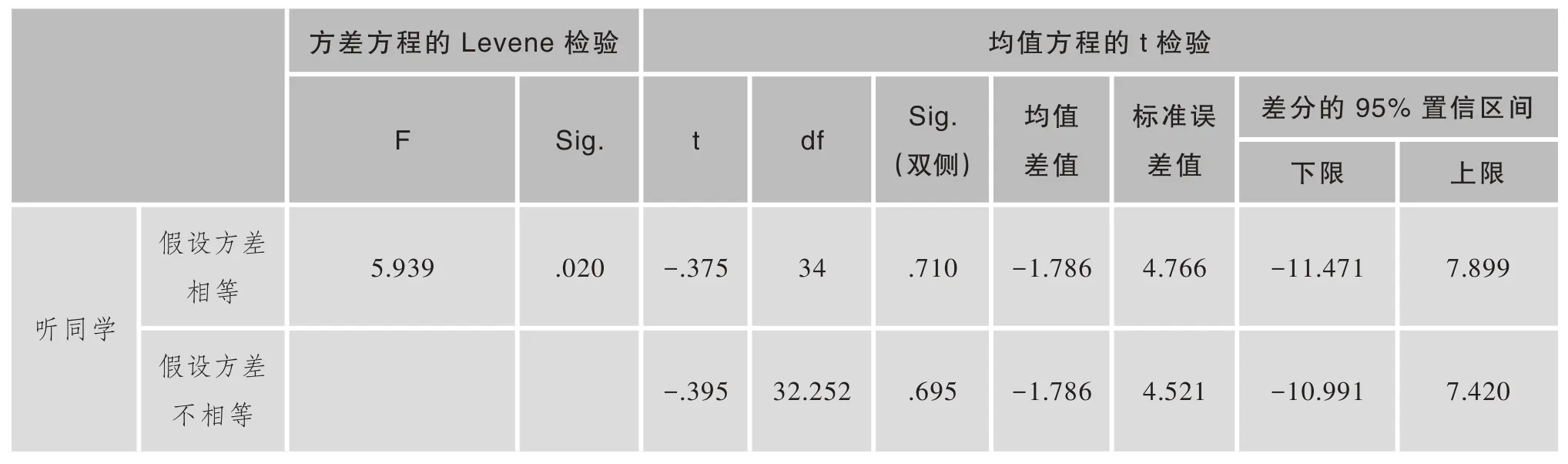
表5 独立样本检验

同理，可以得到，“提问”“评价”“思维操作”“做习题”“静默等待”和“闲聊”的临界置信水平大于5%，说明两节课的这些学习行为没有明显的差异。而“回答”“交流”“记笔记”“发呆”“做小动作”和“打瞌睡”的临界置信水平小于5%，说明两节课的这些学习行为具有明显差异。

四、研究结果的讨论

选取的两节课有一定的代表性，函数单调性是函数模块的重要组成部分，线面垂直判定是立体几何不可缺少的部分，在立体几何的学习起着承上启下的作用。从上面的数据分析，可以得到函数与立体几何的课堂学习行为有着显著的差异。函数课堂的有关学习行为明显多于立体几何的课堂，表现出学习兴趣更加浓烈、课堂气氛更加活跃、与教师的互动更多，归结的原因有以下几点：

（一）知识结构和经验水平不同

函数从初中开始接触学习，学生相对比较熟悉，有一定的学习兴趣，上课能集中精神听讲，主动回答问题，积极参加各种教学活动；而立体几何的知识点是从空间几何体的结构、三视图到表面积体积，再到点、线、面之间的位置关系，学生在高一才开始学习，刚接触有一定兴趣，但是随着后面知识难度的增大，学生失去了兴趣，有的学生为了分数而学，而有的学生甚至放弃学习。已有研究表明，“学生解答几何基本题上表现较差，而对代数基本知识和基本技能的掌握较好。对于中学生来说，几何比代数难学，许多学生连基本题也做不好；其次是两极分化比较严重”。［3］这种差异体现在两节课的“回答”“交流”“记笔记”学习行为有着明显的差异，其临界置信水平小于5%。总之，函数的学习是螺旋式上升，更多地体现学习过程的同化；而立体几何是直线式的学习，更多地体现学习过程的顺应。

（二）数学能力要求不同

函数离不开“数”，“数”是学生从小学开始就接触学习的，而高中函数深化了由常量到变量的认识。立体几何是直观与抽象，直觉与逻辑，猜想与论证相结合的模块，在核心素养培养中，更需要逻辑推理、直观想象和数学建模的能力，恰恰学生在这方面是薄弱的。“对几何学所需要的数学概念的抽象比代数学更为困难。许多人可能会认为，几何学概念的基础是图形，而图形比数量更为直观，因此是容易抽象的。事实上，越是直观的事物、越是与我们的日常生活联系密切的事物就越难抽象。”［4］所以在学习立体几何时，学习兴趣不高，课堂表现平平，学生更容易走神或者有做小动作等学习无关的行为。比如在线面垂直判定这节课中，“倾听行为”和“言说行为”的人数统计量平均值都低于函数单调性这节课的均值，而“无效行为”的平均值是20.07，远高于函数单调性这节课的均值11.64。

（三）教学期望不同

由于函数和立体几何在高考中的比重不同，可能导致教师对立体几何的重视不够。课堂教学是学生获取信息、提高能力和养成思想观念的主渠道［5］，但是在立体几何教学中，存在教学方式单一的现象，有的教师忽略学生的认知水平，直接把知识硬塞给学生，缺乏对学生的思维引导。同时，部分教师为了节约时间就放弃观察或者直接把结论告诉学生，缺少学生自主探究，也缺少立体几何知识与现实生活的联系、缺少知识的拓展和延伸。例如在讲解三棱锥侧面积公式推导的时候，只有少数老师会让学生在课堂上做个三棱锥，然后沿着母线剪开，观察各个部分的联系，从而推导出三棱锥侧面积公式。立体几何的教学为了凸显直观性，教具是必不可少的，而有的农村学校教具比较少甚至没有，有的学校没有多媒体教学，单单靠着黑板和粉笔，教学效果就更加大打折扣，这会造成学生在课堂上的不专心和走神。从统计结果看，两节课的“发呆”“做小动作”和“打瞌睡”等行为的临界置信水平小于5%，说明两节课的这些行为有着明显的差异。

（四）课程结构不同

立体几何分布在必修课程的主题三和选择性必修课程的主题二，内容分布在不同的模块。在整个教学中，立体几何安排的课时是40多个课时，大多数课时都是用来讲授新课，练习、讨论时间少。可见，立体几何的内容多且课时少，所以教师的课堂教学方式大多是讲授式。尽管两节课采用的都是讲授法，在“听同学”“提问”“评价”“思维操作”“做习题”等二级维度学习行为的差别不大，但“听教师”学习行为临界置信水平为0.000，远小于5%，说明两节课的结构有着明显的差异。

五、启示与建议

从上面的分析可知，学生在函数课堂上的表现明显优于在立体几何课堂上的表现，造成这种差异的原因也是多方面的。当然，学生的“学”离不开教师的“教”。由此，从“教”的角度反思立体几何教学中的不足，提出加强立体几何教学的建议是必要的且是有益的。基于函数课堂上的学生学习行为表现，借鉴函数教学的思路，立体几何教学可以加强函数与立体几何的知识融入，渗透函数思想和数形结合方法，丰富学生的数学现实，强化几何直观等，从而促进学生对立体几何知识的理解和牢固。

（一）开拓教学资源，提升思想方法

教学资源的拓展，往往可从知识的联系和转化入手，通过函数和立体几何内容的相互渗透，促进学生融会贯通。两节课的“听教师”有着显著的差异，而它又是新授课的关键，所以在立体几何内容的讲解中可以渗透函数的方法。例如：在棱长为2的正方体ABCDA1B2C3D4中，E、F分别是棱A1D1，A1B1的中点。（1）求异面直线DE与FC1所成的角；（2）求BC1和面EFBD所成的角。本题通过建立空间直角坐标系，运用向量方法来求角，用函数的方法解决立体几何问题。

（二）改进互动方式，促进合理的同化或顺应

在函数教学中，往往可以寻找知识点的联系和不同，促进合理的同化和顺应，如二次函数的学习一般是从一次函数引入，对数函数的学习是指数函数的顺应。由于两节课的“思维操作”没有显著的差异，立体几何的教学往往也可这样处理。例如，直线与平面的平行关系可由直线间的平行关系引入；又如线面垂直的判定和性质其实是互逆的，即线面垂直的判定是：线线垂直⇒线面垂直，线面垂直的性质是：线面垂直⇒线线垂直，两者的同化或顺应水到渠成。“如果学生是被指导着去创造这一切，会容易学会、记住和迁移这些有价值的知识和能力，而如果是被强迫做的，那就不同了。”［6］此外，立体几何还可运用多种教学手段，如游戏、比赛、设置教学障碍等形式，帮助学生集中注意力。

（三）应用现代化信息技术，丰富认知表象

由于个体数学经验和数学现实的不同，导致有的学生无法合理建构立体几何的空间关系。在“互联网+”时代，信息技术的广泛应用正在对数学教育产生深刻影响。《普通高中数学课程标准（2017版）》指出：“要把信息技术作为学生学习和解决问题强有力的工具，致力于改变学生的学习方式，使学生乐意并有更多的精力投入到现实、探究性的学习活动。”因此，教师应注重信息技术与数学课程的深度融合，优化课堂教学，转变教学与学习方式，实现传统教学手段难以达到的效果［7］。例如：某几何体由底面半径和高均为5的圆柱与半径为5的半球面对接而成，该封闭几何体内部放入一个小圆柱体，且圆柱体的上下底面均与外层圆柱底面平行，求小圆柱体积的最大值。此题可以借助几何画板或者3Dmax构造出几何体，设小圆柱底面半径为r，根据小圆柱高h的变化观察体积的变化，在变化中发现有一个直角三角形，满足r2+（h-5）2=52，然后列出体积函数，运用导数求出最值。

（四）通过多元表征，深入理解数学

要充分利用教材，培养学生识图、辨图、画图能力。空间想象能力是学好立体几何必不可少的能力，要注重实物教学，直观感知，丰富学生的表象储备，循序渐进，打好基础。例如，在高一刚接触立体几何时，可以给学生呈现长方体、正方体、柱、锥、球等的实际模型，并指导学生从各个角度观察，在大脑中形成丰富的表象，以此来培养学生的空间想象能力。又如两节课的“倾听行为”和“言说行为”有着显著的差异，所以可以通过函数表征来深入理解立体几何概念。例如已知正方体ABCD-A1B1C1D1中，求异面直线AA1和BD1的距离。此题可以利用向量构建从“形”到“数”的桥梁，转化为函数的最小值问题。