基于Simulink的三连杆机械臂控制器参数化算法

(西安航空职业技术学院,陕西 西安 710089)

现阶段，马宝离与霍伟等人对双臂空间机器人抓无系统动力学及其控制进行了深入探究；陈安军等人详细分析了平面双连杆机构机械臂动力学建模与运动学分析相关问题；肖涛与黄强等人深层研究了给定手作业轨迹的仿人机器人推操作；Mettin U, Hera P L, Freidovich L等人明确指出了基于虚拟约束的控制策略机器人运动轨迹，尤其是三连杆机械臂轨迹跟踪控制设计层面，因为模型复杂性，导致反馈增益求取难度明显增大。谢俊，匡俐辉等人构建了新型串联中医推拿机械臂模型，并进行了运动学与动力学分析，同时基于Adams做了速度与加速度仿真。尽管当前三连杆机械臂研究在不断深入，且获得一定成果，但是针对控制器的参数化设计方式相对繁杂，控制器结构非常复杂[1]。因此本文面向三连杆机械臂进行了控制器设计与直接参数化算法研究，基于三连杆机械臂控制器设计，明确指出简洁的、优化的直接参数化方法，不仅实现了机械臂动力闭环系统特征结构优化配置，还获得所需特征结构，在很大程度上改善了系统整体性能。

1 三连杆机械臂模型分析

就连杆i(1,2,3)而言，mi代表连杆质量；Li代表长度；Lei代表连杆从前关节与中心的具体间距；Ji代表惯性力矩，连杆惯性力矩通过其中心轴与XY相垂直的平面；βi代表连杆与Y轴正半轴向之间的测量角。三连杆机械臂模型[2]示意图具体如图1所示。

为便于计算分析，以此进行明确标记[3]，即

(1)

机械手的运动方程，如式(2)所示：

W(β)β″+V(β,β′)β′+M(β)=Sτ

(2)

式中：τ为控制力矩向量。

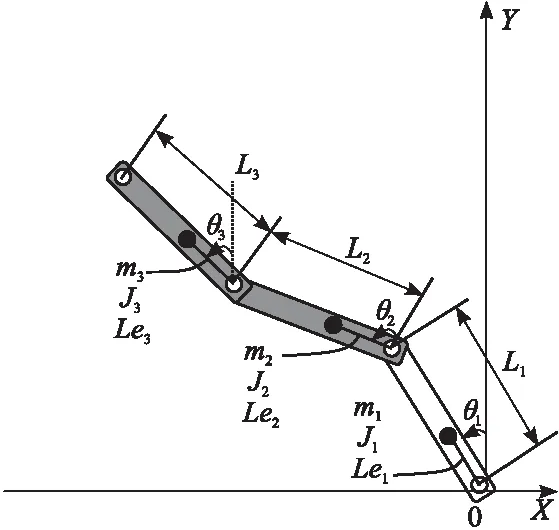
图1 三连杆机械臂

基于三连杆机械臂动态化方程，选择直接参数化算法，通过特征结构进行机械臂运动转移于直立平衡点的控制规律进行优化配置设计，从而保障三连杆机械臂控制的稳定性与可靠性[4]。

面向三连杆机械臂运动要求为闭环系统稳定安全，促使机械臂保持于稳定状态，顺利转移到直立平衡点，即

β=0，β′=0

(3)

就机械手运动方程为载体，合理设计包含两个重要组成部分的机械臂控制器[5]。即

τ=τe+τf

(4)

τe负责补偿系统的M(β)，即

τe=S-1M(β)

(5)

τf为状态反馈控制规律，即

(6)

式中：T0(β,β′)与T1(β,β′)为反馈增益；υ为外部输入信号，一般情况下，在仿真验证时会直接忽视。

将机械臂控制器带入机械手运动方程，可获得闭环系统，即

W(β)β″+[V(β,β′)-ST1(β,β′)]β′-ST0(β,β′)β=Sυ

(7)

2 反馈控制律问题求解

针对反馈控制律问题设计求解，以促使闭环系统成为具备所期望线性系统的特征结构。在具体问题中，W(β)行列式值并非为0。设定：

(8)

那么闭环系统公式可以转变为一阶模式，即

γ′=Ue(β,β′)γ+Se(β,β′)υ

(9)

式中:

(10)

(11)

所以，促使Ue(β,β′)与任何给定相同维度常数矩阵相类似。

具体求解问题可明确描述为此形式，即：问题TLR，给定机械手运动方程，任何选择矩阵集F∈R2n×2n，发现常数非奇异矩阵集N∈R2n×2n与反馈增益矩阵T0(β,β′)、T1(β,β′)，n代表矩阵维数，以满足相关条件，即

N-1Ue(β,β′)N=F

(12)

所以，闭环系统矩阵，即

Ue(β,β′)=NFN-1

(13)

而常数矩阵明确定义为

(14)

后续问题即如何求取相关参数，以促使问题得以圆满解决[6]。

3 直接参数化算法设计

就参数矩阵集选取约束条件与方式方法，其中包含Zariski开集定义，基于相关定理，可给定三连杆机械臂机械手运动方程直接参数化算法具体流程[7]。

首先，矩阵集F结构。所谓矩阵集F一般代表Jordan形或对角形。为保障其为Hurwitz矩阵，要求特征值都保持在复平面左半部分，则

λi(F)∈C-，i=1,2,3…,6

(15)

在遇到特殊情况时，矩阵集F可根据具体情况具体明确，在控制器仿真验证时，选择相对简单的Hurwitz矩阵。

其次，最优化问题。就系统相关标准要求，构建性能指标，即

J=J(F,Z)

(16)

其中，主要关于F与Z标量函数，以此构成以下最优化问题，即

(17)

但是在大多数具体问题中，因为几乎任意矩阵Z都能够满足相关要求，因此约束条件一般都会被忽视。

再次，选取所需参数。通过性能最优化算法，计算选择最优或者次级优化参数矩阵集。在仿真验证过程中，通过前两个步骤引理可知，最优化问题可直接忽略。

然后，控制器反馈增益计算分析。对反馈增益参数化表达式进行计算分析，特殊状况下，通过获得闭环特征向量矩阵N，那么闭环系统矩阵可通过Ue=NFN-1计算获取。

最后，仿真验证。基于数值仿真进行直接参数化算法有效性验证，以证明其在实际应用模型中的实效性。

4 仿真验证分析

构建三连杆机械臂模型，包含三个旋转关节，即主躯干臂与水平面运动、主躯干臂与次躯干臂运动、次躯干臂与吊臂运动。通过对机械臂单次拉伸动作控制仿真研究，证明直接参数化算法应用于机械臂控制器的最终实际效果。

4.1 机械臂模型构建

三连杆机械臂模型构建主要划分为两大部分，即机械臂刚体部分，各个连杆臂与关节之间对接，物理参数设置具体如表1所示；关节控制部分，各关节基于控制信号通过控制器的控制回路对关节旋转进行有效控制[8]。

表1 三连杆机械臂模型参数

其中，重力加速度g为-9.8m/s2。

4.2 控制器参数优化

通过直接参数化算法优化控制器参数的方法面向各个参数寻优，对三连杆机械臂关节响应指标进行综合考察，同时与基于z-n临界比例度法整定的响应结果比较分析。直接参数化算法参数具体即：最大迭代数为104；加速度常数为1.21；惯性权重为0.92；适应度函数指标权重为0.53。三连杆机械臂关节旋转角度以激励信号为依据采取阶跃信号，信号参数具体如表2所示。

表2 控制信号参数

通过z-n临界比例度法与直接参数化算法对控制器参数进行整定分析。两种不同算法整定之后，机械臂关节在既定时间内响应曲线[9]具体如图2～图4所示。

图2 关节一4s以内响应曲线

图3 关节二2s以内响应曲线

图4 关节三2s以内响应曲线

由图2～图4可知，直接参数化算法在进行机械臂关节响应优化之后，并没有出现振动现象，在0.2 s周围到达稳定状态，超调量适宜。由于调节时间较短，可明确机械臂拉伸动作为一步到位，从而直接获得了机械臂的良好控制效果，这就直接证明了直接参数化算法在三连杆机械臂控制器参数优化中的有效性。

此外，基于响应曲线测试的系统响应超调量与调节时间，面向直接参数化算法与z-n临界比例度法在三连杆机械臂控制器参数优化中的实际效果进行对比分析，具体指标[10]如表3所示。

表3 关节响应性能指标

由表3可知，在工业层面应用较为广泛的z-n临界比例度法在三连杆机械臂控制器参数优化中的效果并不显著，但是直接参数化算法在超调量指标层面可获得显著优势，且调节时间较短，这就表明直接参数化算法在三连杆机械臂控制器参数优化中更具优越性。

5 结 论

总之，通过三连杆机械臂动力模型，明确直接参数化算法，有效解决系统特征结构配置问题，促使闭环系统转变为线性系统，并且具备所需特性结构。基于Simulink仿真验证直接参数化算法，结果表明，直接参数化算法不仅简洁可靠，还能获取所期系统动态特征；控制器可实现机械臂稳定运转于直立平衡点位置；直接参数化算法可显著优化机械臂各个关节响应调节时间与超调量，在参数优化后，机械臂拉伸动作关节响应既消除了振动，又减小了超调量，且调节耗费时间非常短。