改进的双曲正切函数的变步长LMS 算法
章坚武,余皓,章谦骅
(1.杭州电子科技大学通信工程学院,浙江 杭州 310018;2.之江实验室智能网络研究中心,浙江 杭州 311121)
1 引言
随着现代通信技术的发展,毫米波通信以及同时同频全双工通信是目前5G 研究中的热点研究领域[1-2]。在这些研究领域中,为更好地进行高指向性波束校准以及相应的信号检测,需要进行干扰噪声的自适应对消,该类问题是目前的研究难点之一。Widrow 等[3]最早在20 世纪80 年代提出了最小均方误差(LMS,least mean square)算法,LMS 算法具有计算简便、实现难度低、适应能力强等特点,在雷达波束成形、干扰噪声自适应对消和新一代移动通信技术等领域被广泛应用[4-8]。
传统LMS 算法的步长为定值(下文称为定步长LMS 算法),不能同时满足快速收敛和低稳态误差的要求。鉴于此,为了改善定步长LMS 算法的性能,研究者开展了大量的研究。文献[9]提出了基于S 函数的变步长LMS 算法,该算法利用S 函数控制步长变化,使步长因子在收敛初期取得一个较大值,在接近或达到收敛时,赋予步长因子一个较小值。相较于定步长LMS 算法,变步长LMS 算法具有更快的收敛速度和更低的稳态误差。但在趋于收敛时,由于S 函数的特性,该算法在接近原点时曲线过于陡峭,会导致步长因子取值迅速变化,使算法在稳态时的误差变大。文献[10]将S 函数经过平移翻转变换,并引入参数改善了S 函数的底部变化,获得了较好的性能,但由于该算法模型过于复杂,影响了算法的灵活性。文献[11]则基于具有S函数曲线特性的Q 函数,并利用补偿项的相对误差互相关函数控制步长的更新,提出了一种新的变步长LMS 算法,由于Q 函数的特性,该算法同样面临着收敛时稳态误差大的问题。文献[12]使用了梯度的统计平均控制步长因子,提高了算法的收敛速度并获得了较好的稳态误差性能,不足是该算法的抗干扰性能较差,且引入的判断门限使算法的复杂度过高。文献[13]通过引入指数函数,提出了基于指数函数的变步长算法,但该算法在运行过程中使用了过多的指数运算,同样导致算法的复杂度过高。文献[14]在文献[13]的基础上,将其中的变步长方法用于部分滤波加权系数的更新,提高了收敛速度,并降低了复杂度。然而,在低信噪比环境下,该算法在接近收敛时的步长较大,导致稳态性能较差。文献[15-16]则建立了步长因子与迭代次数的非线性关系,可以提高算法的收敛速度,同时改善了抗干扰性能,但它们的跟踪性能却明显不足。
综上所述,已有的变步长算法不能同时较好地解决噪声干扰、系统跟踪性能差、稳态误差较高等问题。为了解决以上问题,本文提出了基于改进双曲正切函数的变步长LMS 算法(IVSSLMS,improved variable step-size LMS),该算法在双曲正切函数的基础上,利用误差信号的相关值和步长反馈因子,共同调节步长因子的取值,使算法在保证快速收敛的同时,降低稳态误差,并提高了算法的系统跟踪性能。与已有变步长算法对比,本文所提算法具有更优异的性能。
2 定步长LMS 算法
自适应滤波器的原理框架如图1 所示。输入信号x(n)经过未知系统与外界噪声v(n)叠加后形成期望信号d(n),x(n)经过自适应滤波器后的输出信号为y(n)。将期望信号d(n)与输出信号y(n)相减得到误差信号e(n)。e(n)反馈给自适应滤波器来更新自适应滤波器的加权系数向量,使更新后的输出信号更加接近于期望信号,从而达到自适应滤波的目的。
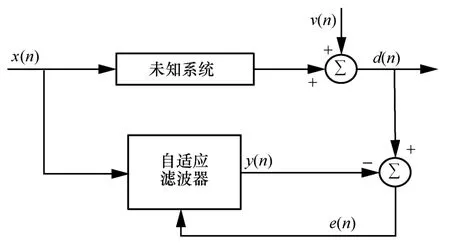
图1 自适应滤波器原理框架
自适应滤波器的输出信号y(n) 为
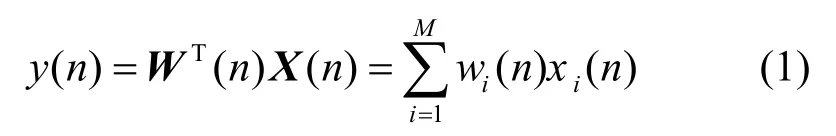
其中,X(n)=[x(n),x(n−1),…,x(n−M+1)]T,W(n)=[w(n),w(n−1),…,w(n−M+1)]T均为自适应滤波器的加权系数向量,M为自适应滤波器的阶数。误差信号e(n)为期望信号与自适应滤波器输出信号之差,其值为
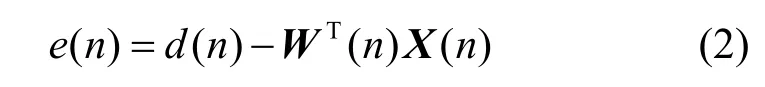
误差信号的均方误差(MSE,mean square error)E[e2(n)]为

LMS 算法自适应滤波器的加权系数更新式为

其中,μ为步长因子,其值为常数;∇(·)为求梯度。
对均方误差的梯度向量∇I进行估计,如式(5)所示。
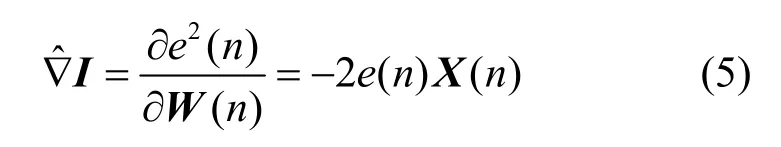
联立式(4)和式(5)可得
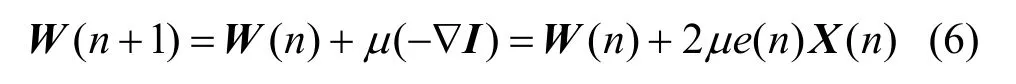
定步长的LMS 算法的流程为
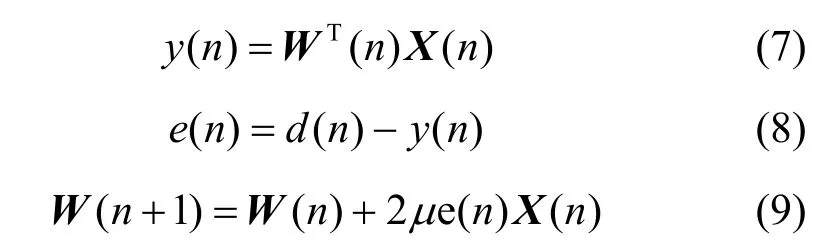
由文献[1]可知,LMS 算法的收敛条件为

其中,λmax为自适应滤波器输入信号自相关矩阵的最大特征值。
3 改进的变步长LMS 算法
传统的定步长LMS 算法中步长因子为恒定值,不能同时改善收敛速度和稳态误差性能,为了解决这种问题,各种变步长算法被提出。覃景繁等[17]给出的步长选取原则为步长因子在算法初期应取得一个较大值,使算法能够快速收敛,当算法趋于收敛时,使步长因子取得一个较小值,以减小稳态误差。

由于步长因子为正值,将式(11)变成偶函数,即

文献[18]在双曲正切函数的基础上,利用误差信号的相关值e(n)e(n-1),代替e(n)减小了随机噪声的干扰,并通过引入参数改善了步长因子的底部特性,一定程度上解决了定步长LMS 算法的缺陷。但该算法的系统跟踪能力略显不足,因此,为了加强步长与输入信号的关系,使算法具有良好的跟踪能力,本文在文献[18]的基础上加入一个步长反馈因子J(n),J(n)的表达式如式(13)所示。
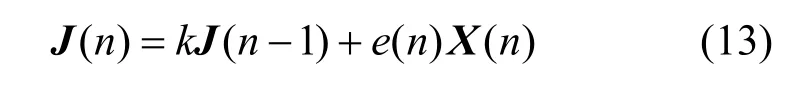
将误差信号的相关值e(n)e(n−1)代替e(n),并把J(n)的二范数作为自变量代入式(12)中,得到式(14)。
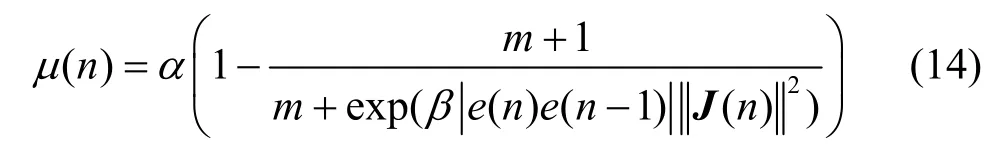
为防止输入信号功率突然增大导致算法发散,在加权系数向量更新时,加入“归一化”算法对μ(n)进行限制,即

其中,φ是为了避免分母过小而设置的常数,取值为0.01。
至此,IVSSLMS 算法流程可总结为
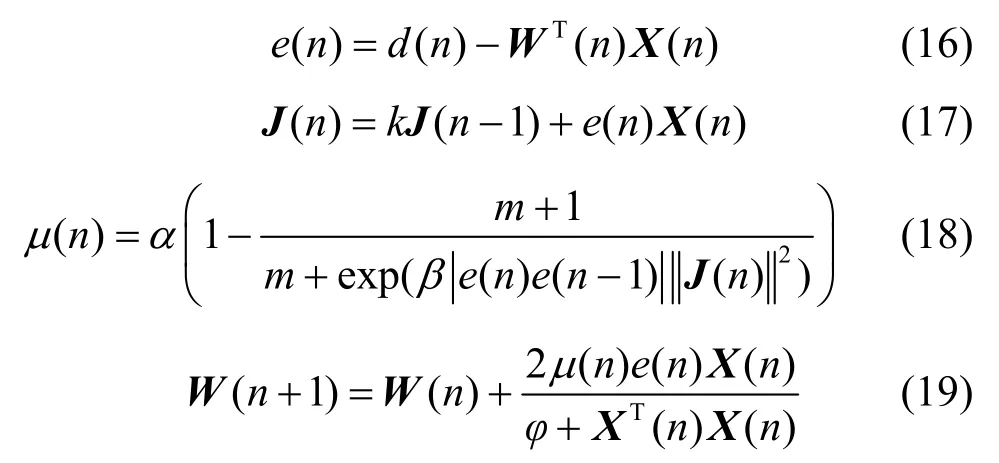
由式(18)可知,当e(n)→0时,;当e(n)→∞时,,即μ(n)的最大值为α。由式(10)可得,IVSSLMS 算法的收敛条件为
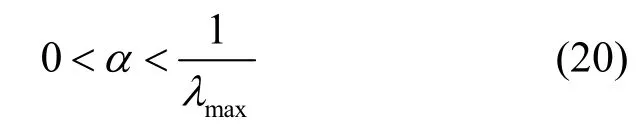
4 算法理论分析
4.1 参数选择
本节通过误差函数与步长因子的关系曲线,将IVSSLMS 算法中参数对步长的影响进行讨论分析,关系曲线如图2 所示。其中,图2(a)为β=20、m=600、k=0.6,α分别为0.1、0.2、0.3 时的步长曲线;图2(b)为α=0.3、m=600、k=0.6,β分别为15、25、50时的步长曲线;图2(c)为α=0.3、β=20、k=0.6,m分别取60、600、6 000 时的步长曲线;图2(d)为α=0.3、β=20、m=600,k取0.3、0.6、0.9 时的步长曲线。
从图2 可以看出,参数α对步长的取值起到了至关重要的作用。随着α的增大,步长的取值也较大,即在满足式(20)的情况下,较大的α能获得较大的步长,算法能获得较高的收敛速度。
参数β、m、k对步长函数的形状影响较大。可以看到,β越小,m越大,k越小,则在同一误差值下,步长的取值越小。另外,由图2(d)可以看出,若k选的过大,误差信号还未为0 时,步长因子就已经为0 或几乎为0,这将严重减缓算法的收敛速度。因此,在实际的工程运用中,需要对α、β、m、k的取值进行折中考虑。

图2 各参数变化时μ(n)与e(n)曲线
4.2 算法抗干扰性分析
式(18)中涉及随机性的因子只有e(n)e(n-1)||J(n)||2,采用统计平均来分析系统的抗干扰能力。步长反馈因子J(n)=kJ(n−1)+e(n)X(n),其中,J(0)为零向量,将步长反馈因子进行简化得到
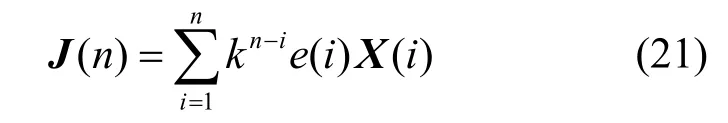
计算e(n)e(n-1)||J(n)||2的期望为
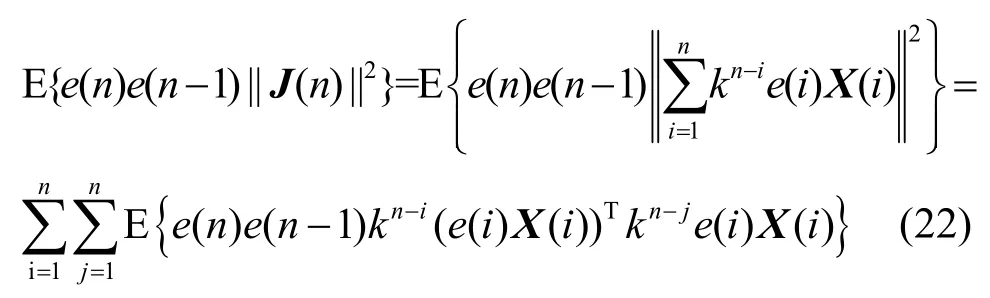
由式(22)可以得到,当i≠j时,由于0<k< 1,n→∞,E{e(n)e(n−1)||J(n)||2}=0,即此时的步长变化对算法没有干扰。
当i=j时,式(22)可以写成
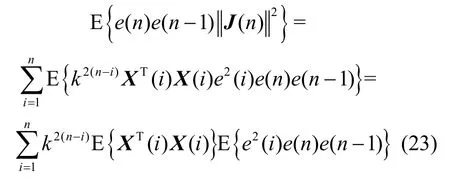
由式(23)可知,系统的统计平均特性不含噪声v(n),系统不受独立噪声v(n)的影响。因此IVSSLMS算法利用调节步长因子可以提高算法的抗干扰能力。
5 仿真分析研究
5.1 算法参数对性能的影响分析
本文的所有仿真在MATLAB R2016a 软件下进行。设自适应滤波器的阶数M=6,假设未知系统为横向FIR(finite impulse response)结构,抽头系数为[−0.580 6,0.653 7,−0.322 3,0.657 7,−0.058 2,0.289 5],在迭代次数N=500 时将系统的抽头系数设置为[−0.580 6,0.485 6,−0.238 7,0.159 6,−0.325 4,0.102 5]。假设自适应滤波器的输入信号x(n)和干扰噪声v(n)均为0 均值的高斯白噪声,x(n)的方差为1,v(n)的方差为0.001,即信噪比为30 dB。系统的取样点数为1 000,每条学习曲线均为200 次独立仿真后求其统计平均的结果。参数α和β变化时的学习曲线如图3 所示。
图3(a)是β=3 000、m=10、k=0.9,α分别取0.1、0.5、0.8、1.0、1.5 时的学习曲线。分析图3(a)可知,在α从0.1 增加到1.5 的过程中,算法的收敛速度越来越快,但稳态误差也相应提高。当α=0.1 时,算法达到稳态的次数为200 左右;当α=1.5 时,算法达到稳态的次数为50 左右,但α=1.5 时的稳态误差较大。经过仿真验证,α为0.8 左右时算法性能较优异。在工程应用中,α的取值首先需要分析输入信号的统计特性,其次还要使α值满足式(20)。
图3(b)是α=0.8、m=10、k=0.9,β分别取2、25、200、3 500、40 000 时的学习曲线。分析图3(b)可知,随着β的增大,算法的稳态误差和收敛效果都逐渐变好。当β分别为3 500 和40 000 时,两者的收敛速度和稳态误差接近。为了降低系统的计算量,提高算法的运行速度,经过仿真验证,β为3 500左右时算法性能较优异。
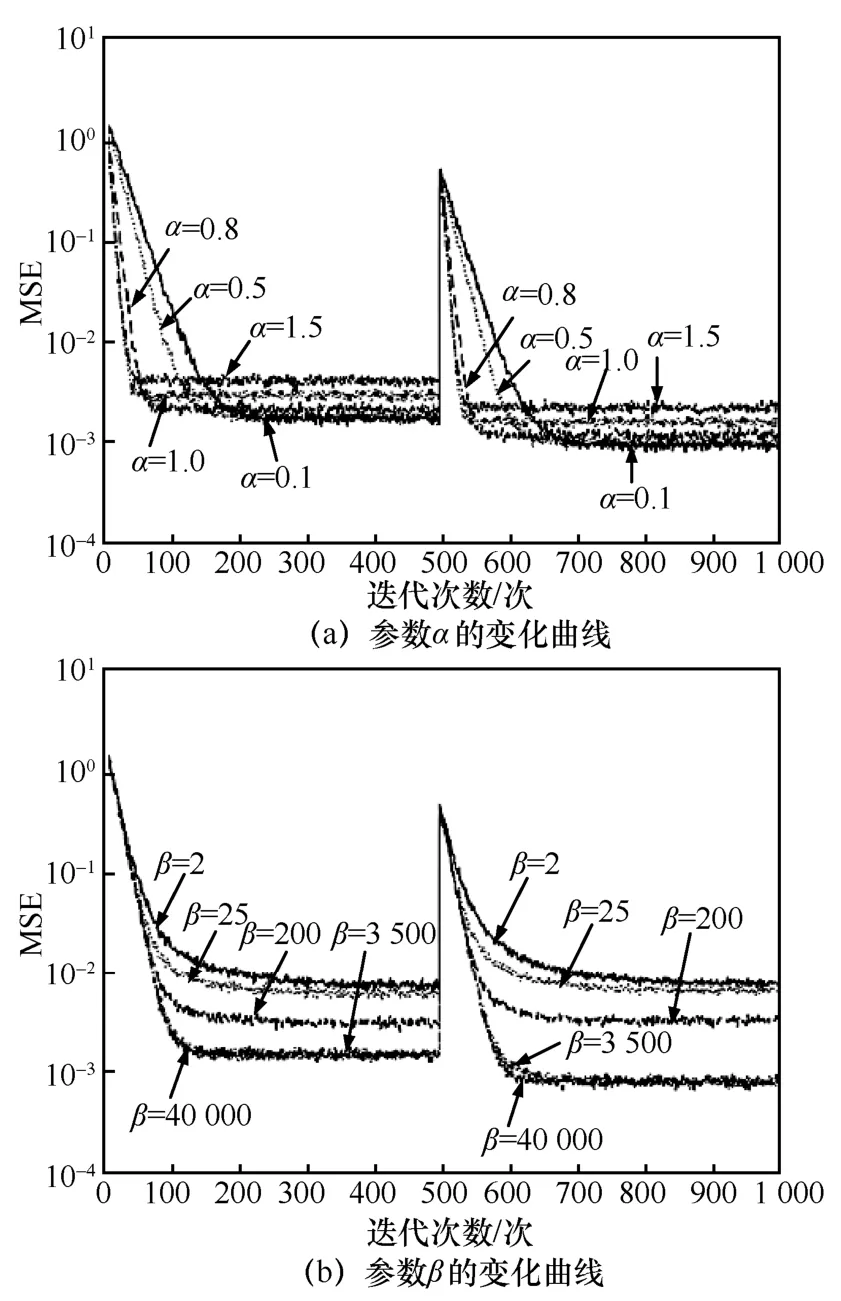
图3 参数α 和β 变化时的迭代次数与均方误差曲线
参数m和k变化时的学习曲线如图4 所示。
图4(a)是α=0.8、β=3 000、k=0.9,m分别取1、15、150、5 000、10 000 时的学习曲线,分析图4(a)可知,m=1 时的学习曲线与m=15 时学习曲线的收敛速度相近,但m=15 时的稳态误差较低。经过仿真验证,m为15 左右时算法性能较优异。
图4(b)是α=0.8、β=3 000、m=1 000,k分别取0.6、0.7、0.8、0.9、1.5 时的学习曲线,分析图4(b)可知,参数k越大,对应算法趋于稳态时的误差越小。但k的值过大会导致算法的收敛速度降低,如k=1.5 所示。经过仿真验证,k为0.9 左右时算法性能较优异。
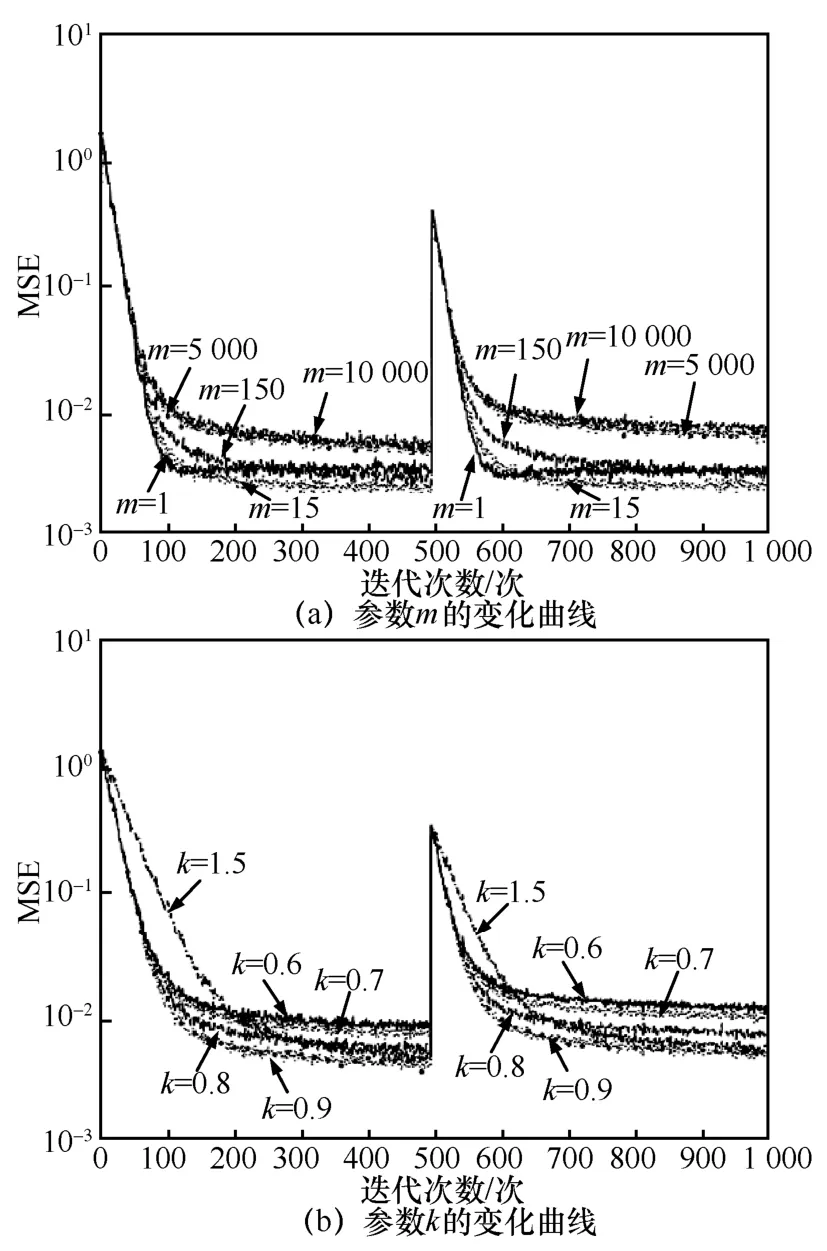
图4 参数m 和k 变化时的迭代次数与均方误差曲线
5.2 算法稳健性分析
本节将分析IVSSLMS 算法的稳健性,仿真设置的环境与5.1 节设置的环境相同,算法参数设置为α=0.85、β=3 500、k=0.9、m=15。不同信噪比下算法的学习曲线如图5 所示。
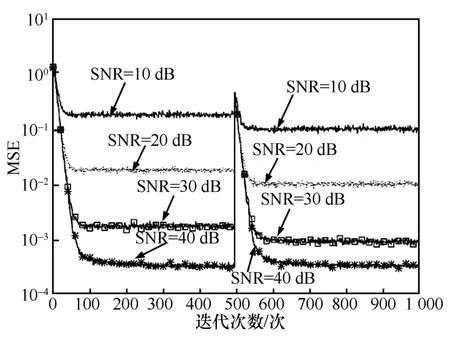
图5 不同信噪比下的学习曲线
由图5 可知,在IVSSLMS 算法达到稳态后,随着系统参数的改变,IVSSLMS 算法仍可以快速恢复到收敛状态,这表明IVSSLMS 算法具有较好的跟踪能力。在低信噪比条件下,IVSSLMS 算法仍可以保持良好的性能,这表明IVSSLMS 算法具有良好的稳健性。
6 多种变步长LMS 算法性能对比
本节将IVSSLMS 算法与文献[18-21]这几种变步长算法在信噪比分别为30 dB 和15 dB 时进行仿真,仿真设置的环境与5.1 节设置的环境相同。几种变长算法对比如表1 所示。
系统取样点为1 000、每条曲线均为200 次独立仿真后取平均的结果,仿真结果如图6 所示。
由图 6(a)可知,当信噪比为 30 dB 时,IVSSLMS 算法的收敛速度和稳态误差性能均明显高于其他4 种变步长LMS 算法,文献[18]算法在系统响应发生变化时,收敛速度和稳态误差性能均受到严重影响,表明该算法的系统跟踪能力较差。文献[19]算法的稳态误差较高。文献[20]算法的收敛速度快于文献[21]算法,但稳态误差高于文献[21]算法。由图6(b)可知,当信噪比为15 dB 时,文献[18-20]算法的收敛速度均快于文献[21]算法,但稳态误差低于文献[21]算法。文献[21]算法的稳态误差接近于 IVSSLMS 算法,但IVSSLMS 算法的收敛速度比文献[21]算法快了2 倍以上。通过以上对比分析可知,在高低信噪比背景下,相比于这4 种变步长LMS 算法,IVSSLMS算法的收敛速度优势明显,稳态误差也较低,对外界系统的适应性也更强。
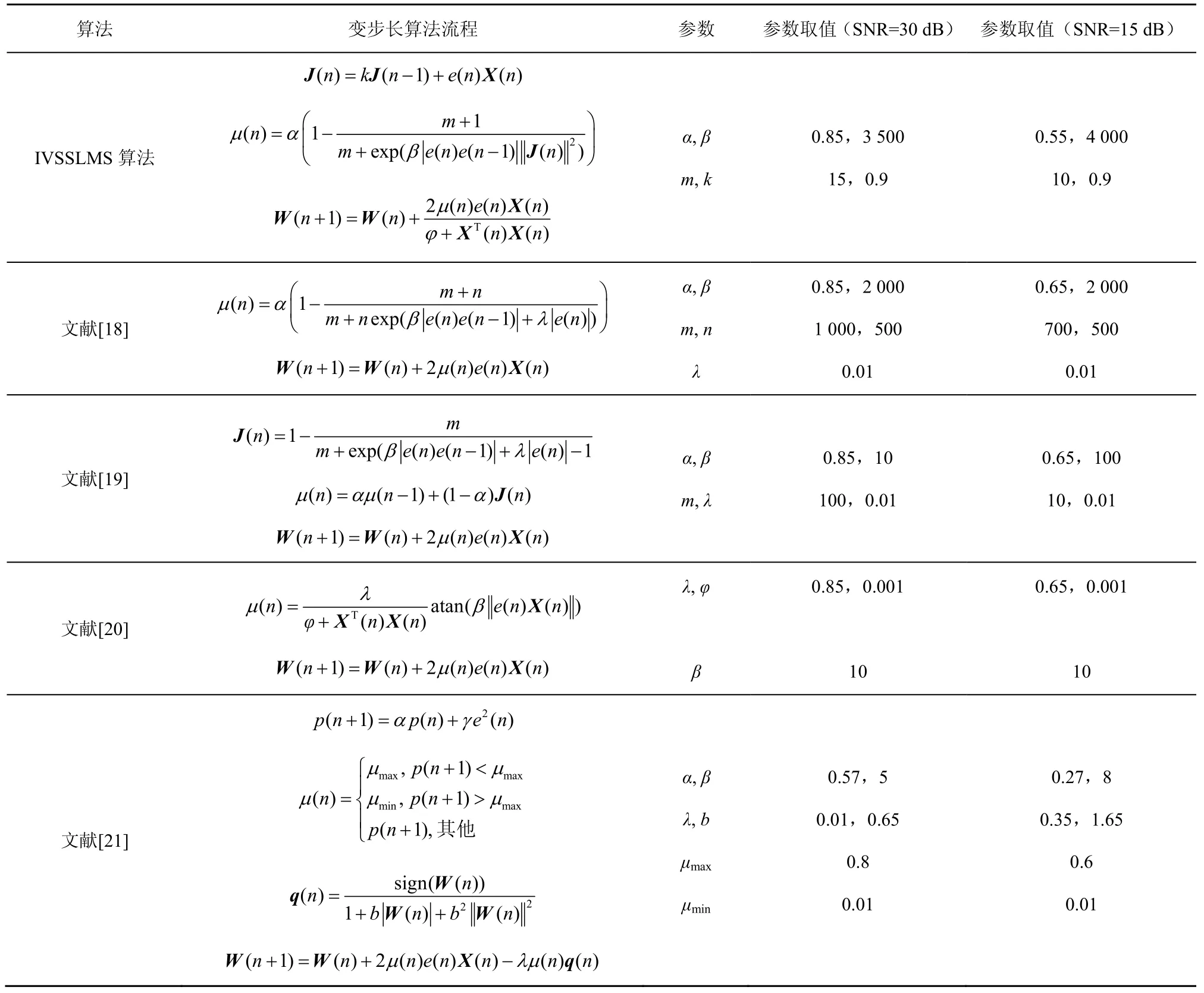
表1 几种变步长算法对比
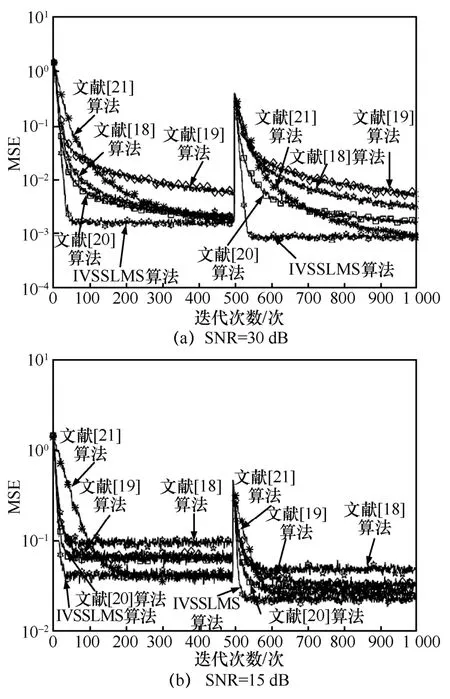
图6 不同信噪比环境下各算法的学习曲线
7 结束语
本文分析了多种已有变步长LMS 算法,提出了一种新的变步长算法IVSSLMS。该算法基于改进的双曲正切函数,引入步长反馈因子和误差信号的相关值控制步长因子的更新,使在收敛初期步长获得较大值提高算法的收敛速度,在趋于收敛时步长获得恒定的较小值减小稳态误差。仿真实验表明,IVSSLMS 算法在高/低信噪比下的性能相较于其他变步长算法更优异。但IVSSLMS 算法引入的参数较多,与其他变步长算法相比计算量稍大,但以目前的硬件水平是完全可以接受的,因此IVSSLMS 算法具有广阔的工程应用场景和较高的实际应用价值。

