面向嵌入式的残差网络加速方法研究

甘 岚，李 佳，沈鸿飞

(华东交通大学 信息工程学院，南昌 330000)

1 引 言

目前，基于深度学习[1]的图像分类识别与嵌入式设备相结合已成为智能化产业发展的新趋势.在嵌入式设备中，参数较少的机器学习算法难以对复杂的图像数据维持较高的分类准确率.卷积神经网络CNN[2]可以更有效的对图像进行精确分类[3-5].但卷积网络的参数量极大，在广泛应用的嵌入式平台存在运行速度慢、难以部署的缺点.因此，实现精度更高的卷积神经网络在嵌入式端的部署加速具有重要的研究意义.

深度残差网络是近年来较为流行的网络结构，席志红[6]利用残差网络对医学图像混合数据集进行分类实验.相比其他方法，残差网络有效的减少了参数和训练时间，提高了网络性能.Michal Gregor[7]提出了一种结合迁移学习的残差结构分类器，该分类器能够很好的实现在外界环境严重干扰下的停车位影像的分类.这些实验表明了残差网络相比其它分类网络，拥有更好的网络性能.残差网络以跳跃式残差结构作为基本结构，这种结构很好的解决了网络变深的性能退化问题，且这种结构计算压力相对较小、易于优化，更适合在嵌入式端部署.但是残差网络自身参数量较大，直接运行在嵌入式端需要很大的存储资源和计算资源.

网络加速方法可以有效减少网络的计算量和存储量，是实现残差网络在嵌入式端加速应用的重要手段.网络加速可以从网络结构入手，通过结构优化和卷积分解等方法来减少参数和计算量，但是对于一些复杂网络卷积分解过多会降低网络性能，同时卷积分解后网络中BN层数量增多，会占用大量计算资源；也可以对网络模型进行压缩，通过去除网络冗余使得网络稀疏化[8-10]和网络参数定点化处理[11-13]等方法来实现网络加速，但一些优化后的网络结构，由于网络复杂度较低，网络模型的压缩会导致网络性能大幅降低.网络优化可以优化网络结构，模型压缩可以有效去除网络冗余参数.因此，如何结合网络优化和模型压缩技术来降低网络参数，保证网络性能，实现残差网络在嵌入式端最优加速是本文研究的重点.

本文根据上述问题，结合不同加速方法的优势提出一种更有效的嵌入式网络加速方法.该方法首先为了减少原始残差结构的参数，采用深度可分离卷积、线性优化的方法对原始残差结构进行卷积优化，并设计能够维持网络性能，参数更少的残差网络；其次，为了将改进的残差网络在嵌入式端实现最优加速，采用混合网络剪枝、合并BN层与卷积层、随机取舍的FP16量化的方法继续减少网络中冗余参数以加速网络，并与常规方法进行性能比较.实验结果表明，使用上述方法对可以有效实现残差网络在嵌入式端的优化加速.

2 网络加速方法

2.1 卷积优化

卷积优化是通过更高效的卷积结构保证网络性能，并减少网络参数来实现网络加速的.如Squeezenet[14]的fire module结构，通过控制进入3×3卷积的特征数量来降低计算量，但该结构适合于浅层网络.

深度可分离卷积应用于很多高效神经网络[15-18]，如MobileNet、ShuffleNet、Xception等.它由一层深度卷积和一层逐点卷积组成，通过输入通道的线性组合来计算新的特征.比较深度卷积和传统卷积的输出，假设输入一个N×H×W×C特征，通过k个3×3的卷积，pad=1，普通卷积的输出特征映射为N×H×W×k.对于深度可分离卷积，特征提取过程为：第一层的深度卷积可以将输入分为C组，并收集每个通道的特征；第二层的逐点卷积将上层的输出通过1×1的逐点卷积来收集每个点特征，最终通过深度可分离卷积的输出特征映射也为N×H×W×k.使用深度可分离卷积替代标准卷积，计算量减少了8倍，输出的特征映射数量没有变化.可以在几乎没有精度损失的情况下大幅度降低参数量和计算量.卷积分解会使得卷积的输出维度降低，网络中的非线性函数会对较低的输出特征造成影响，过多分解会造成网络的性能急剧下降.

但是，过多的卷积优化分解会使得网络性能急剧下降，而且由于卷积分解使得卷积输出的维度降低，网络中的非线性函数会对较低的输出特征造成影响.因此如何平衡卷积分解数量保证准确率是卷积优化的核心问题.

2.2 访存优化

访存优化是通过减少网络训练和推理时内存的读写次数来实现网络加速的.残差网络卷积分解后网络中的卷积层和BN层数量会增多，BN层的作用是对数据进行归一化处理，它可以加快网络收敛，防止过拟合现象出现[19].但是BN层在网络推理时需要很大的计算资源，BN层增多会占用更多内存资源，从而影响网络的推理速度.

网络的BN层主要是对卷积层的输出数据进行处理，因此直接去除可能会造成一定的精度损失，如何维持网络精度和减少BN层内存消耗是BN层访存优化的重点.合并BN层和卷积层，可以将两层的计算融为一次计算，该方法不会改变BN层输出结果，可以维持网络的精度，并通过减少网络计算时访问内存的次数来实现网络加速[20].

2.3 模型压缩

模型压缩是通过对网络模型的参数进行精简化，在保证网络性能的同时降低网络计算和存储开销来实现网络的加速.常见的方法有：网络剪枝、参数量化、参数共享、网络分解等[21].参数共享依赖于聚类效果，过高的压缩比会造成精度下降.网络分解是通过矩阵分解对模型进行压缩加速，但是对于维度较低的1×1和3×3卷积核，分解难以实现网络加速.网络剪枝和量化是广泛应用于卷积神经网络的压缩加速方法.

网络剪枝[22]是通过去除网络中不重要的连接，降低网复杂度实现网络加速.在网络卷积层和全连接层中，存在大量输出值趋近于0的神经元，这些神经元对网络影响较小，去除后不会影响网络性能.靳丽蕾[23]通过混合剪枝方法有效的去除vgg-16网络中影响较小的参数.网络剪枝可以有效的降低网络中的冗余参数，降低计算量，剪枝核心问题是寻找评判机制，去除网络中不重要的节点或卷积核.

网络量化是对网络参数定点化处理来实现网络加速的.训练生成的模型文件存储的参数一般为32位的浮点型数据，大部分的存储是由分数部分占据.模型量化就是通过将高位的数据向低位的数据进行映射来获得更小的数据表示范围和更稀疏的数值来有效的降低内存消耗的.而且，CNN网络对噪声和扰动的鲁棒性较强，训练的权重一般会在一个较小的范围，量化后只会造成较低的精度损失.量化过程中数据的变换必须保证是线性的，这样计算结果才能够映射原始值.量化的重点是确定合适的量化范围和映射关系.

残差网络对一些复杂的图像具有良好的特征提取能力，但是网络层数较深，模型参数较多，存储体积较大，不适合在嵌入式等硬件资源或缺的平台上直接应用.单一的模型加速方法对网络加速效果是有限的，通过卷积优化可以对网络结构进行优化且保证网络性能，剪枝和量化技术分别是从参数的重要性评判和存储方式两个独立的方向实现网络加速.综合使用这些方法才可以最有效的降低网络参数，达到网络最优加速.但是，在卷积优化和剪枝后的网络复杂性降低，不同形式的量化可能会造成差异较大的精度损失.

3 残差网络优化与设计

3.1 残差结构优化

3.1.1 残差结构

目前，残差网络有两种主流的残差结构，它们使用了不同的卷积核的连接方式.第一种是由两个3×3的标准卷积串联而成，输入特征会通过两个标准卷积处理后输出，这种双卷积结构具有较强的特征提取能力，但是网络参数相对较多，一般用于40层以下的残差网络，常见的有ResNet34.第二种残差结构首先使用1×1的卷积将输入特征数量压缩4倍，再通过3×3的标准卷积进行特征提取，最后使用1×1的卷积将输出特征数量扩张4倍，这种结构针对第一种残差结构的卷积参数较多的问题，通过1×1卷积有效的减少了网络中的参数.

对于一个标准卷积K，假设输入特征映射W，输出特征映射为G，它们的尺寸分别为(Df,Df,M)、(Dg,Dg,M,N)，其中M，N分别表示为输入和输出通道数，标准卷积K的大小为(Dk,Dk,M,N)，那么卷积的计算公式表示为.

Gk,l,n=∑i,j,mKi,j,m,n·Fk+i-1,l+j-1.m

(1)

输出特征为时(Dg,Dg,N)，卷积的计算量为.

Dk·Dk·M·N·Df·Df

(2)

假设两种输入输出特征映射均为(Df,Df,M)和(Dg,Dg,N)，那么第一种残差结构的计算量为.

2·3·3·M·N·Df·Df

(3)

第二种残差结构的计算量为.

M·N·Df·Df/4+3·3·M·N·Df·Df/16
+M·N·Df/4

(4)

在输入特征相等的情况下，第二种残差结构的参数数量比第一种结构减少了16.94倍.但是第二种结构在初始维度较低时特征提取能力相对较弱，一般需要初始特征维度较大，才能保证其特征提取能力，而且模型的层数一般相对较深，这样使得相等残差结构组成的残差网络，第二种结构比第一种结构参数更多.

3.1.2 结构优化

本文针对嵌入式平台资源短缺问题，提出一种参数较少的残差结构：该结构使用3×3深度可分离卷积和普通卷积串联而成，对于1×1逐点卷积我们去除了ReLu激活函数，使用线性瓶颈来降低非线性Relu激活函数对深度可分离卷积输出特征的影响.改进后的残差结构的输入特征映射为64维与第一种残差结构相似，结构如图1所示.

图1 改进的残差结构Fig.1 Improved residual structure

对比计算发现，采用深度可分离卷积对标准卷积进行分解，当深度卷积的尺寸为(Dk,Dk,1,M)输出特征为(Dg,Dg,M)；逐点卷积尺寸为(1,1,M,N)，输出特征也为(Dg,Dg,N)，计算公式表示为.

(5)

深度可分离卷积的计算量为.

Dk·Dk·M·N·Df·Df+M·N·Df·Df

(6)

最终，深度可分离卷积减少的计算量为

(7)

3.1.3 线性瓶颈

当一个输入特征维数嵌入到比激活空间低的多的子空间中时，消除较窄层中的非线性可以实现更好的网络性能[24].当一个2维数据经随机矩阵T将数据映射为M维，并通过非线性ReLU激活函数处理后，再利用T的逆矩阵由M维逆恢复到原始的维度.当映射维度M=2，3时，恢复后的结构发生了严重的坍缩，当映射维度M>15时，恢复后的结构较好.这表明了，这表对于一个低维数据进行ReLU等线性变换时，特征会相互重叠，导致较严重的信息丢失，维度较高时，恢复的信息才会增多.使用线性变换替代Bottleneck的激活层，可以有效的减少非线性激活函数对改进的残差结构造成的信息损失.

深度卷积输出维度较低，非线性的ReLU激活函数可能会滤除很多有用信息.因此，本实验剔除了第二层1×1卷积ReLU激活函数.

3.2 残差网络设计

网络结构:原始的ResNet34和ResNet50都是由16个残差结构串联的残差块组成.因此本文利于优化后的残差结构，根据常见ResNet网络基础设计了一个50层的残差网络ResNet50_dw，结构如图2所示.

图2 残差网络结构Fig.2 Residual network structure

改进的残差网络分为6个阶段，第1阶段使用7×7的卷积进行初始特征提取，输出为特征维度为64；第2至5阶段分别由多个输出为64维，128维，256维，512维的改进的残差块串联而成，其中第2阶段和第5阶段由3个残差块相连接，第3阶段由4个残差块相连接，第4阶段由6个残差块相连接；第6阶段使用全连接层输出，每层卷积层后分别使用Batch Normal正则化处理.图2中MaxPool为最大池化操作，AvgPool为平均池化操作，整个网络保留了较多的传统卷积，维持了网络的复杂性和特征提取能力.

4 混合加速方法

优化后的残差结构相比于原始的两种残差结构参数分别减少了43.6%和40.3%，但单一的网络卷积优化后，网络模型参数及复杂度依旧很高.剪枝、优化BN层和量化技术分别是从参数的重要性评判、计算方式和存储方式三个独立的方向实现网络加速，混合三种方法可以继续对网络加速，但是优化剪枝后网络的复杂性会大大降低，量化和优化BN层可能会造成精度损失的差异，因此本文将继续研究最为合适的混合加速方法，以保证网络的性能.加速过程为：首先通过评估参数对初始网络的卷积核进行有效裁剪，再对训练后的网络模型进行卷积层和BN层的合并，最后将模型中的浮点型数据进行定点化处理.实验将对比合并BN和卷积层和去除BN层，以验证最优BN层优化方法；对比随机取舍的FP16量化与常见的TensorRT INT8量化方案，以验证最优量化方法.

4.1 网络剪枝

4.1.1 剪枝过程

网络剪枝可以有效的剔除卷积层和全连接层中影响较小的参数，网络剪枝过程为：第1步利用数据集训练生成网络模型文件；第2步根据网络模型文件记录的每个通道和卷积核的权重分布情况来衡量卷积核的重要性，确定剪枝百分比；第3步根据百分比删除本层的待剪枝卷积核及特征图对应关系，第4步在卷积核剪枝后，通过再训练恢复模型精度.最后重复上述过程，逐层对剩下的卷积层进行剪枝和微调，剪枝完成后输出最终网络模型文件.

本文中衡量各层卷积核重要性的标准是卷积核权重绝对值之和，即L1范数.将每层卷积层的卷积核权重之和由大到小排序，权重之和较小的卷积核，其特征提取的信息相对较少，对网络贡献较小，这些卷积核的重要性较低.每层卷积层剪枝的比例通过卷积层的敏感度来衡量，敏感度是指在不同卷积层删除相同卷积核时对精度的影响关系，精度损失越严重说明该卷积层敏感度越高，对于这样的卷积层要删除较小比例的卷积核或不做处理，敏感度较低的卷积层要删除较大比例的卷积核.

4.1.2 剪枝计算量

裁剪一层卷积后，假设它的第i个卷积层输入特征的高度和宽度分别为hi和wi，原始输入通道数为ni，输出通道为ni+1，上层卷积层裁剪比例为p，本层裁剪比例为q，那么对于输入特征图xi∈Rni×hi×wi，经过ni+1个k×k三维卷积核F∈Rni×k×k，输出特征图为xi+1∈Rni+1×hi+1×wi+1原来的运算量为:

C=nini+2k2hi+2wi+1

(8)

剪枝后的本层的计算量减少为:

C<(1-P)ni,(1-q)ni+1>=(1-)ni(1-q)ni+1k2hi+2wi+1

(9)

输入本层卷积核剪除后，同时也会去除下层的输入映射，那么假设下层输出特征图ni+2保持不变，剪枝后计算量总共减少了:

C<(1-p)ni,(1-q)ni+1,ni+2>=nini+1k2hi+1k2hi+1wi+1+

ni+1ni+2k2hi+2wi+2

(10)

显然，对于深层的残差网络，卷积核剪枝可以有效的加快模型的运算速度和减少参数，对网络模型具有良好的加速效果.

4.2 BN层优化

优化后的残差网络BN层数量增多，BN层推理时会占用较大的内存资源，融合BN层和卷积层计算可以有效解决网络的运算时的内存问题.该方法过程为：首先网络卷积层的计算是通过将输入x乘以权重w后和偏执b相加得到的，计算公式为:

(11)

BN层是对卷积层的输出结果减去全局均值，再除以标准差，计算公式为:

(12)

两层融合后即可得到新的权重参数和偏执值，最终计算公式为:

(13)

合并两层后，原始网络的BN层输出值并没有产生变化，从而不会对网络精度造成影响，而网络的参数的计算和读取次数会大幅的降低.

4.3 参数量化

4.3.1 TensorRT方案

嵌入式端低比特的数据会比高比特的数据运算速度更快，数据量化就是将浮点型数据转化为定定点型数据.目前最常见的量化方式基于NVIDIA TensorRT的int8量化方法，普通的int8量化方式是直接将所有真实值映射在int8上，这种量化方式虽然简单直接，但是会浪费大量位宽，甚至会导致准确率的大幅降低.TensorRT方案为了解决这一问题，采用了饱和技术来防止精度损失，通过设置阈值T，将阈值内的数据进行映射，阈值外的数据直接采用-128和127，量化过程中虽然舍弃了部分数据，但可以节约大量存储空间.TensorRT将32位浮点型数据映射为8位整型数据的映射公式为：

FP32_Tensor(T)=scale_factor(sf)*bit_Tensor(t)

+FP32_bias(b)

(14)

其中bias偏置值去掉对精度的影响较小，因此去除偏置值，最终的映射公式为：

T=sf·t

(15)

4.3.2 FP16量化

在内存中一个32浮点型数据表示形式为1bit符号位+8bit的指数部分+23bit的尾数部分，浮点数的实际值为符号位乘以指数偏移值再乘以分数值，将32位浮点数据转化为FP16半精度浮点型后，数据指数部分和尾数部分别用5bit和10bit表示，网络可以降低一半的存储空间.FP16相比INT8可以表示更广的数值范围.

传统的定点数据转化规则是最近邻取舍原则，定义方法为：

Round(x,)=

(16)

其中，表示这个定点数，IN为定点数的整数位，FL为定点数的小数位，为最小单位=2-FL，但是这种方式在样本数据不平衡时，预测偏差较大.随机取舍的方式拥有更好的量化性能，在数据产生上溢时，随机选取会选择与它最接近的两个数之一，选取的概率与他们之间的距离成反比，当数据产生下溢时，使用最大值或最小值代替，最终转化方式为：

(17)

(18)

5 实验结果及分析

本实验训练的软件环境为：ubuntu16.04操作系统，使用Tensorflow-GPU深度学习框架完成模型训练.硬件配置为i7处理器，16G运行内存，显卡为GTX2080ti.测试环境为Jetson TX2嵌入式开发板，内存为8GB、存储为32GB.

网络训练设置初始学习率为0.01，训练批次大小为100.实验采用的数据集为cifar10，由10个不同类别的32×32彩色图像组成，其中每个类别有6000张图像，分为5个训练集共5000张图像和1个测试集共1000张图像.

5.1 优化网络性能分析

实验使用卷积优化后的50层的残差网络对比两种常规的残差网络，本实验对数据集和超参数进行相同的处理和设置，在相同的条件下对比三种网络的性能，首先设置训练迭代的次数为50000次，每20000次降低一次学习率，训练迭代时将cifar10数据集随机裁剪为28×28像素.最终三种的残差网络的精度和损失变化，如图3所示.

图3 三种网络训练损失和精度变化Fig.3 Three loss and accuracy changes of network training

相比ResNet34，改进后的网络收敛速度略低，但整体收敛趋势一致；相比ResNet50，改进的残差网络在训练初期收敛速度更快，最终收敛速度损失比较接近.可见，优化后的残差网络能够维持较强收敛速度和泛化能力.

继续对比三种残差网络的平均准确率，前20000次改进的残差网络和原始的ResNet34精度变化速率相似，ResNet50精度变化速率稍缓.通过降低学习率再训练最终三种网络的最高准确率分别为：ResNet34为88.24%，ResNet50为87.62%，ResNet50_dw为87.79%.实验表明：优化后的残差网络相比于原来ResNet50精度提升了0.17%，略低于ResNet34，网络依旧维持在较高的准确率.

网络的存储量和检测速度是评判模型是否在嵌入式端实现加速的重要指标.本实验使用平均单张图片的检测时长作为网络检测速度的评判标准.为此，实验进一步对比三种残差结构生成网络模型所需存储体积和检测时长.对比结果如表1所示.

对于改进残差结构组成的残差网络，相比于ResNet34和ResNet50存储空间分别减少了40.5%、46.2%，平均单张图片的检测时长分别减少了33.2%、39.3%.改进的残差网络相比于常规的残差网络在检测速度和存储量上都有了明显的降低，且在精度上没有较大损失.可见，改进的残差网络更适合在嵌入式端加速应用.

5.2 混合加速性能分析

5.2.1 网络剪枝

实验使用改进的残差网络，前期实验发现卷积核的数量为64和128的卷积层，敏感度较高，不适合进行剪枝；卷积核的数量为256和512的卷积层，敏感度较低，存在冗余参数较多，为了维持网络模型的精度，实验只对网络最后两个阶段，共9个残差结构进行卷积核剪枝.对256维卷积设置剪枝比例为30%，512维卷积设置剪枝比例为50%，能够保证最好的准确率.改进的网络最后一次剪枝后的模型再迭代的损失和准确率变化情况如图4所示，实验迭代次数为1000次，在1000次前网络已经趋于稳定，学习率为0.001.

剪枝后的模型准确率相比之前模型的准确率在初始状态时有所降低，通过再训练后，改进残差网络精度分别恢复到87.34%，精度损失较低.再对比模型的平均测试速率和存储体积，剪枝后的残差网络模型在损失较低精度的情况下，存储体积降低为23.0MB，比剪枝前降低了54.6%，平均单张图片的检测时长为72.9ms，减少了31.8ms.

5.2.2 BN层优化

实验对比去除不同比例BN层的方法和合并BN层和卷积层的方法来验证最优的BN层优化方案.由于残差网络减少较少BN层，网络的检测速度提升较低，网络加速不明显.因此本实验对比了去除残差网络中常规3×3卷积共16层BN层、去除3×3深度可分离卷积共32层BN层和去除除第一层以外所有共48层BN层的三种残差网络与原始的残差网络的性能变化.实验使用的残差网络均保留了第一层7×7卷积的BN层，维持网络对初始特征的归一化处理，以防止网络拟合现象出现.最终网络的精度和速度的变化如5图所示.

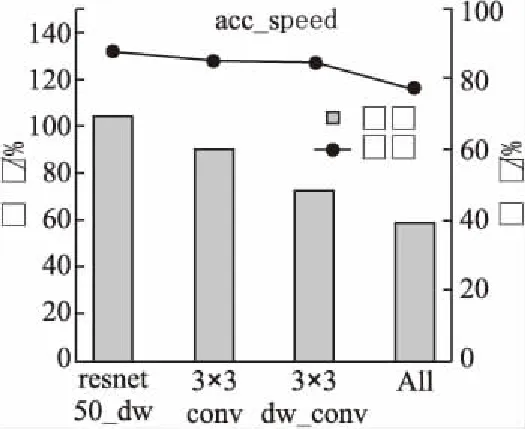
图5 残差网络精度和速度变化Fig.5 Accuracy and speed changes of residual network

实验表明去除网络中的BN层网络的检测速度最高可加快43.9%，但是网络精度损失10.63%，精度损失严重.去除部分BN层也存在一定的精度损失，因此直接去除BN层会造成网络的性能损失.

进一步实验，将改进后的模型和剪枝后的模型分别进行BN层和卷积层合并，并与原始网络进行比较，最终网络精度和平均单张图片的检测时长如表2所示.

表2 改进的残差网络优化BN层性能变化Table 2 Performanc changes of the improved residual network optimizing BN layer

相比直接去除BN层，合并BN层和卷积层后，网络的检测速度提升了12.6%，且维持了原始的网络准确率，剪枝和优化BN层后检测速度提升了39.1%，实验表明该方可以有效解决BN层计算量大的问题.

5.2.3 模型量化

对优化卷积和BN层的残差网络模型文件分别进行INT8和FP16量化，量化后的性能比较如表3所示.残差网络模型经过INT8和FP16量化后的存储体积分别降低了74.3%和49.1%，平均单张图片的检测时长分别提高了47.7%和24.2%，但是常规的TensorRTINT8方案量化后模型精度降低了2.63%，性能损失严重，基于随机取舍的FP16量化精度只降低了0.56%.

表3 残差网络量化性能变化Table 3 Performance changes of residual network quantitative

实验结果表明：两种量化方法，都使得模型明显提速，满足了一般嵌入式设备的内存要求.但是常见的TensorRT的INT8量化虽然压缩比例较高，网络精度损失严重；基于随机取舍的FP16量化可以在保证网络的性能的前提下，更有效的实现网络加速.

5.3 实验结果分析

本文实验对比了常规的残差网络、卷积优化后的残差网络和结合卷积优化和混合加速的残差网络最终的精度、存储和速度变化如图6所示.

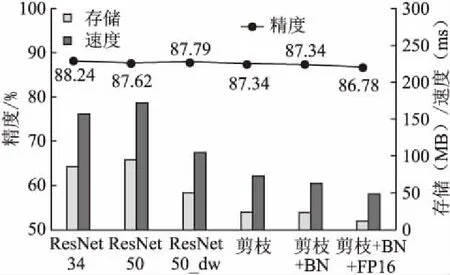
图6 各残差网络性能比较Fig.6 Performance comparison of each residual network

实验结果表明：卷积优化后的残差网络可以维持常规残差网络的准确率，而且网络存储体积和计算速率都有了明显的下降，具有更好的网络性能.混合加速方法中，模型剪枝可以剔除大量影响相对较小的卷积核，让模型的存储体积减少58%左右，且模型的精度损失较低；BN层和卷积层的合并可以加快12.6%推理速度；模型INT8量化和FP16量化可以使模型的存储体积缩小了4倍和2倍左右，计算速率提升47.7%和24.2%，但传统TensorRTINT8存在着较高的精度损失，基于随机取舍的FP16精度损失较低.最终本文选择结合卷积优化和混合剪枝、合并BN层和卷积层和FP16量化加速的方法，可以在降低较小的精度的情况下，大幅减少参数和存储量，实现网络最优加速.

6 结束语

本文主要研究了基于嵌入式的残差网络的加速方法，首先使用深度可分离卷积对传统卷积进行有效分解；其次使用线性瓶颈模式减少了非线性层对输出特征的影响；再次设计了与常规残差网络精度和损失相似，但参数量更少、计算速度更快的残差网络；最后混合剪枝、合并BN层和卷积层和FP16量化加速方法继续减少和规范残差网络参数，实现在嵌入式端的加速和应用.与传统加速方法相比，本文使用的方法可以更有效的减少残差网络的存储体积，提高运算速率，实现网络加速.但本文使用的方法还是存在较少的精度损失.在未来的工作中，还需要进一步研究卷积核裁剪指标和量化阈值以提高模型准确率和运算速率，实现深度神经网络在嵌入式端的加速与应用.