一种高维向量空间K近邻快速搜索方法

徐 国 天

(中国刑事警察学院 网络犯罪侦查系，沈阳 110854)

1 引 言

K近邻(K Nearest Neighbor，KNN) 算法是指给定一个待查点，在多维向量空间样本点集合内查找与待查点最接近的K个样本点，如果这K个样本点中的大多数属于某一类别，则待查点也属于这一类别[1].K近邻搜索在很多数据分析问题中得到广泛应用，例如机器学习、地理信息系统、人工智能，等领域.在面对高维、海量样本集合时，因需要与大量样本点计算和比较空间距离，造成计算量大，查询速度慢的问题，影响了KNN算法的实践应用.

针对KNN算法计算量大、查询效率低的问题，目前主要有以下改进方向：1)对样本集进行裁剪.例如文献[2]通过对样本集进行分析，从中剔除冗余元素，缩小样本集合，进而减少K近邻搜索阶段的计算量.但在面向高维、海量样本集时，样本集合缩减规模有限，仍面临计算量大的缺陷；2)采用并行计算架构提升K近邻查询速度.文献[3]提出一种基于CUDA模型的并行KNN算法，采用通用矩阵乘提升距离计算速度，根据K值大小，分别采用两种方法对距离进行比较，这一并行计算方法有效提高了K近邻查询效率；3)采用空间分区数据结构，实现K近邻快速搜索.对样本点集合按照特定的几何形态进行划分，同时构造搜索二叉树，在K近邻查找阶段，通过比较空间距离，对二叉树进行剪枝处理，减少需要计算和比较距离的样本点数量，进而加快K近邻查询速度.常见的空间分区数据结构包括Metric-tree，Ball-tree，Cover-tree，VP-tree，MVP-tree，R-tree和KD-tree[4].各种空间分区数据结构主要在以下三个方面存在区别，第一：分区的几何形状；第二：建立搜索树的空间划分策略；第三：利用数据结构进行搜索的策略[5].Ball-tree结构采用超球体对数据集进行划分，在K近邻查询方面有更多的优势，因此得到广泛应用.但是基于Ball-tree结构的K近邻算法初始K个近邻点位置固定，即Ball-tree结构最左侧K个叶节点，如待查点距离初始K个近邻点空间距离较近，则剪枝效果好，会有更多的数据点被剪枝滤除，进而获得更快的K近邻查询速度.但当待查点距离初始K个近邻点较远时，剪枝半径过大，剪枝效果差，仅有少量数据点被剪枝滤除，K近邻查询速度降低，在面对高维、海量样本集时，这一缺点尤为明显.

针对Ball-tree结构K近邻搜索算法初始K个近邻点位置固定导致的查询效率较低问题，本文提出一种基于“双树”结构的K近邻搜索方法.这种方法从原始数据点集合中过滤出极少量数据点构成剪枝树，过滤剩余数据点构成被删树，剪枝树需要最大限度地保留原始数据点集合在高维空间的分布形态.在查询阶段，由于剪枝树内数据点个数很少，可以快速定位最近邻点，再利用这个近邻点作为被删树的初始近邻点，在被删树内搜索K近邻.由于初始近邻点位置不再固定，而是位于待查点附近，有效缩小了剪枝半径，改善了剪枝效果，提升了K近邻查询效率.

2 基于Ball-tree结构的K近邻搜索方法

Ball-tree是多维向量空间内全部样本点按照一定规则构成的一棵二叉树，每棵子树对应一个子超球体，包含若干个样本点.在K近邻查询阶段，从根节点开始对Ball-tree进行遍历搜索，通过计算待查点和每棵子树超球体质心的空间距离，实现对子树的快速剪枝，进而加快检索进程.

2.1 Ball-tree构造方法

本文研究的Ball-tree结构由Moore提出.Ball-tree的构造过程如下，初始条件下，多维向量空间内全部样本点构成一个最小超球体(对于二维空间，即是最小圆)，这个超球体就是Ball-tree的根节点root.之后按照一定原则将全部样本点划分为两部分，构造成两个最小子超球体，这两个子超球体分别是root节点的左右子树根节点，这个分裂过程持续进行下去，直至每个子超球体内只包含1个样本点或半径极小时停止分裂，Ball-tree构建成功.本文采用加权空间欧氏距离作为多维向量空间内样本点之间的距离计算公式.

Ball-tree内每个Node点包括五个重要属性，质心pivot(即子超球体的圆心)；半径radius，满足公式(1)；样本点集合points(即子超球体内全部样本点数据集)；Child1和Child2分别是Node节点的左右子树根节点，如果Node是非叶节点，则满足公式(2)和公式(3).

(1)

(Node.Child1.points)∩(Node.Child2.points)=ø

(2)

Node.Child1.points∪Node.Child2.points=Node.points

(3)

Ball-tree内每个Node节点的分裂原则如下：首先计算子超球体内距离质心最远的样本点point1，再计算距离point1最远的样本点point2，将全部样本点集合points划分为两个子集Child1和Child2，其中距离point1更近的样本点被划分到Child1集合，距离point2更近的样本点被划分到Child2集合[6]，节点分裂原则可用公式(4)描述.

x∈Node.Child1.points|x-point1|<|x-point2|
x∈Node.Child2.points|x-point2|≤|x-point1|

(4)

图1展示了Node1节点的分裂过程，二维空间内7个样本点A-G构成一个最小圆，即Ball-tree中的Node1节点.距离质心最远的是A点，距离A最远的是B点，A和B点之间的超平面将全部7个样本点划分为两个子集Child1和Child2，这两个子集又构成两个最小子圆，即Node1节点的左右子树根节点.

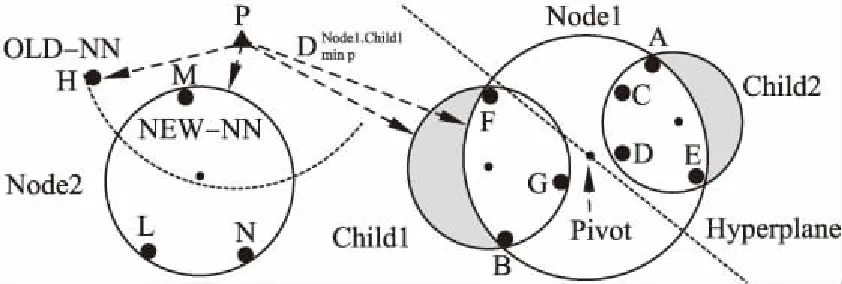
图1 Node节点分裂过程及最短距离计算方法Fig.1 Node splitting and shortest distance calculation

2.2 K近邻搜索算法

多维空间内待查点p与Node节点内任意样本点x的空间距离满足公式(5)和公式(6).下面进行简单证明，根据三角不等式可以得到|x-p|≥|p-Node.pivot|-|x-Node.pivot|,给定x∈Node.points，满足|x-Node.pivot|≤Node.radius，因此可证明公式(5)成立，同理可证明公式(6)成立[7].

|x-p|≥|p-Node.pivot|-Node.radius

(5)

|x-p|≤|p-Node.pivot|+Node.radius

(6)

公式(7)中root为Ball-tree结构根节点，Dmin pChild1为待查点p与Child1节点最小可能空间距离计算公式，这是根据公式(5)给出的边界限定以及子节点内所有样本点必须被其父节点覆盖这一事实得出的.这个性质意味着Dmin pChild1永远不会小于其祖先的最小距离Dmin pNode.图1显示了Dmin pNode1.Child1的计算过程，经过比较确定待查点p到Node1节点的最小距离Dmin pNode1作为p到Node1.Child1节点的最小距离值[8].

(7)

在查询阶段，利用公式(7)可实现对子树的快速剪枝，加快检索进程.如图1所示，当前距离待查点p的最近邻点是H，由于Dmin pNode1>|p-H|[9]，因此Node1节点内的全部7个样本点均被剪枝过滤，不需要逐个计算与p点的空间距离，并比较与|p-H|的大小关系[10]，因此可以加快检索进程.由于Dmin pNode2<|p-H|,因此需要对Node2节点内的3个样本点逐一计算与p的空间距离，比较与|p-H|大小关系[11]，经过三次比较，确定样本点M为待查点p的最新近邻点.

基于Ball-tree结构的K近邻递归搜索算法1：search_KNN(KNN_result,node,target,K)[12].

输入参数：当前最近邻数组KNN_result，首次调用时为空数组；当前处理节点node，首次调用时为Ball-tree根节点；待查点target；待查最近邻个数K.

输出参数：待查点target的K个最近邻数据点.

Step 1.如果当前处理节点node为空，则执行Step 7，否则执行Step 2.

Step 2.如果当前处理节点node为叶子节点，则执行Step 3，否则执行Step 4.

Step 3.令node节点的全部n个数据点组成集合S，S={S1,S2,…,Sn}，其中Si为node节点的第i个数据点.依次取出集合S中的每个数据点Si，计算待查点target与数据点Si之间的空间距离distance；令整数变量len为最近邻数组KNN_result的元素个数，如果len=K，则比较distance与KNN_result[0][1]的大小，KNN_result[0][1]为KNN_result数组首个元组的distance值，如果distance=KNN_result[0][1]，则不更新KNN_result数组.

Step 4.令当前处理node节点对应的球半径为radius，对应的质心点为center，质心点center与待查点target的空间距离为distance_c，如果|distance_c|>radius+KNN_result[0][1]，则执行Step 7，即当前节点内不可能存在待查点target的K近邻数据点，当前节点node对应的整棵子树被剪枝过滤.如果|distance_c|<=radius+KNN_result[0][1]，则执行Step 5，即当前节点内可能存在待查点target的K近邻数据点，需要分别处理node节点的左右子树.

Step 5.令当前节点node的左子树根节点为node.child1，递归调用K近邻搜索算法search_KNN(KNN_result,node.child1,target,K)处理node节点的左子树.

Step 6.令当前节点node的右子树根节点为node.child2，递归调用K近邻搜索算法search_KNN(KNN_result,node.child2,target,K)处理node节点的右子树.

Step 7.算法结束，返回当前KNN_result.

2.3 查询效率分析

根据KNN搜索算法1可知，无论待查点在多维空间什么位置，KNN_result数组的初始值均为Ball-tree结构最左侧K个叶节点.这导致当待查点距离初始K个叶节点较近时，剪枝效果好，查询效率高，反之剪枝效果差，查询效率低，下面通过实例分析.

图2 Ball-tree实例Fig.2 Ball-tree instance

图2显示的是二维空间内44个样本点构成的一棵Ball-tree结构,待查点target在二维空间内的坐标位置为(80,400)，表1显示的是target在二维空间内5近邻搜索过程.初始条件下Ball-tree最左侧5个叶节点(即20，8，39，41，44)被填入KNN_result数组，数组元素按照distance值降序排列.之后算法从左至右，逐个计算叶节点与target的空间距离，并与KNN_result数组首个元素的distance值比较大小关系，动态更新KNN_result数组元素值，使其始终保存当前的5个最近邻.由于target距离初始5近邻空间距离较近，剪枝效果好，查询过程中Ball-tree整个右分枝子树被剪枝，其包含33个样本点.整个查询过程只比较了11个样本点与target的距离值即完成5近邻搜索，查询效率较高.

表1 理想情况下，基于Ball-tree结构的KNN搜索实例Table 1 Best KNN search case based on Ball-tree

表2所示例子中，待查点target在二维空间的位置为[66,212]，这个位置距离Ball-tree结构最左侧5个叶节点，即初始5近邻较远，整个查询过程中剪枝效果较差，只进行了两次剪枝操作，共包括10个样本点.经过与34个叶节点比较空间距离，完成5近邻搜索，查询效率较低.

造成原始Ball-tree结构K近邻搜索算法查询效率较低的原因如下：当KNN_result数组中元素个数不足K个时，将最先处理的叶节点存入KNN_result数组，使其元素个数尽快达到K个，之后不断用更优的近邻点更新KNN_result数组，直至算法结束.这个原始算法的主要缺点在于不论待查点target位于多维空间什么位置，KNN_result数组中初始K个数据点均是固定的，即Ball-tree结构最左侧K个叶子节点.在多维空间内，待查点target的位置是随机变化的，而每个target点的初始K个近邻点均是固定的，这K个初始近邻点很可能距离目标target较远，使用这K个初始近邻点对Ball-tree进行剪枝，因剪枝距离过大，很难达到理想的剪枝效果.如果能在待查点target附近快速找到一组相对近邻点，并用这组数据点作为初始近邻点对Ball-tree进行剪枝，因剪枝距离缩短，将有更多的子树被剪枝滤除，减少空间距离计算和大小比较次数，进而提高整体查询效率.

表2 非理想情况下，基于Ball-tree结构的KNN搜索实例Table 2 Worst KNN search case based on Ball-tree

3 基于“双树”结构的K近邻搜索方法

针对原始Ball-tree结构初始K近邻点位置固定带来的查询效率较低问题，本文提出一种基于“双树”结构的K近邻搜索方法，首先从原始数据点集合中过滤出极少量数据点组成剪枝点集合，过滤剩余数据点组成被删点集合.过滤原则是剪枝点集合中数据点需要最大限度地保留原始数据点集合在多维空间中的分布形态，这样待查点在剪枝点集合中的最近邻点与待查点在完整集合中的第K个近邻点非常接近.利用剪枝点集合构成剪枝树(reduce-tree)，利用被删点集合构成被删树(pruned-tree)，由于剪枝点集合中数据点个数很少，因此可以在剪枝树(reduce-tree)内快速定位最近邻点，再利用这个近邻点作为初始近邻点，在被删树(pruned-tree)和完整树(Ball-tree)内搜索K近邻，由于不同的待查点target，初始近邻点均在target附近，因此可以加快剪枝速度，提升整体查询效率.

3.1 剪枝树reduce-tree和被删树pruned-tree构造方法

在原始Ball-tree构造算法中增加一步处理，对每棵子树信息进行统计，统计结果存入node_density数组.node_density数组中每个元素对应一棵子树的统计信息，统计信息包括这棵子树内数据点个数，即叶节点个数point_num，这棵子树对应的超球体半径radius，这棵子树对应的数据点集合points.数组元素按照每棵子树内数据点个数point_num降序排列，point_num值相同的元素，按照半径radius升序排列.

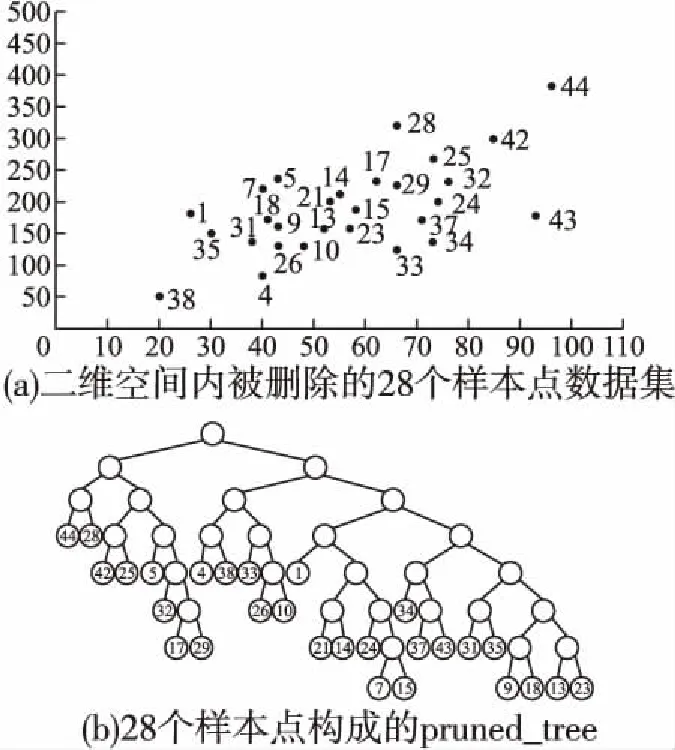
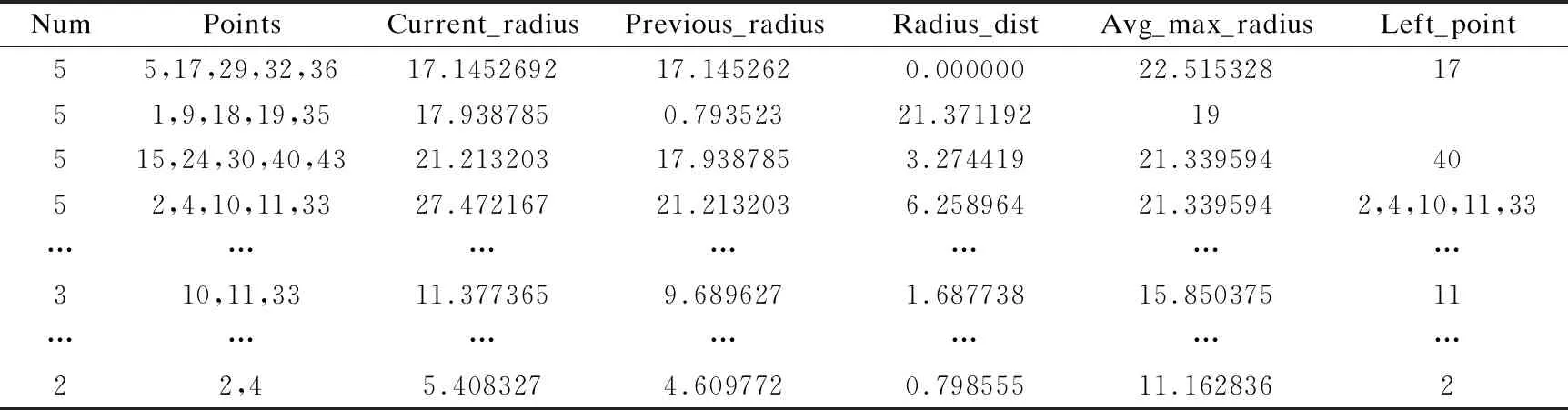
“双树”构造算法2的基本思想是对数据点个数point_num

整数变量max_points用于限定剪枝力度，增大该值将有更多的数据点被剪枝删除，这一数值的确定需要经过精确计算，以达到最佳效果，算法4用于确定这个变量的具体值.图3显示了对二维空间内3960个样本点进行剪枝处理，调整剪枝数max_points的剪枝效果比较，可见剪枝剩余样本点密度不同，但均最大限度保留原始样本点的基本形态，且离群点得到最大限度地保留.

图3 max_points值对剪枝效果的影响Fig.3 Effect of max_points on pruning effect

剪枝树和被删树构造算法2：reduce_and_pruned_tree(node_density,data,max_points)：

输入参数：待剪枝的数据点集合data；存储每棵子树统计信息的node_density数组，数组元素按照每棵子树内数据点个数point_num降序排列，point_num值相同的元素，按照半径radius升序排列；整数变量max_points表示最大剪枝点数，其初始值由算法4确定；

输出参数：一棵由被删除数据点构造的被删树pruned_tree，一棵由剪枝剩余数据点构造的剪枝树reduce_tree.

Step 1.令pruned_tree数组存储被删除数据点，初值为空；令reduce_tree数组存储剪枝剩余数据点，初值为空；

Step 2.将node_density数组中数据点个数point_num>=max_points的全部元素构成集合T，T={T1,T2,…,Tn}.按照数据点个数将子树分类，定义实数变量avg_max_radius表示已经剪枝的每棵子树的最大半径平均值，初值为T1.radius；定义整数变量current_point_num表示当前处理的这类子树数据点个数，初值为T1.point_num.定义实数变量previous_radius表示前一棵子树对应球体的半径，初值为T1.radius.定义整数变量i，初值为2.

Step 3.从集合T中取出元组Ti，如果Ti.point_num!=current_point_num，即当前这类子树处理完毕，则执行Step 6，否则执行Step 4.

Step 4.如果abs(Ti.radius-previous_radius)<=2或者Ti.radius

Step 5.令center为数据点集Ti.points的质心，min_dist_point为点集Ti.points中距离质心center最近的点，令pruned_tree=pruned_tree∪(Ti.points-min_dist_point)，即将Ti.points中除min_dist_point之外的其它数据点并入pruned_tree数组.令previous_radius=Ti.radius，同时更新avg_max_radius值.令i=i+1，如果i<=len(T)，则执行Step 3，否则执行Step 7.

Step 6.令current_point_num=Ti.point_num，更新当前处理的这类子树的数据点计数current_point_num，执行Step 5.

Step 7.令reduce_tree=data-pruned_tree，执行Ball_tree(pruned_tree)构建全部被删数据点构成的被删树，执行Ball_tree(reduce_tree)构建全部剪枝剩余数据点构成的剪枝树，算法结束.

图4显示的是图2所示44个样本点按照算法2构造成的reduce-tree结构，max_points值设置为10，剪枝剩余16个样本点，图5是按照算法2构造的pruned-tree结构.表3显示的是一段局部剪枝过程，前三棵子树均有五个叶节点，且都符合剪枝条件，每棵子树只保留距离子球体质心最近的数据点，其余四个数据点被删除.第四棵子树与前一棵子树球体半径差为6.258964，大于临界值，且球体半径大于全部已剪枝子树球体半径均值，因此不予剪枝处理，这棵子树全部5个叶节点(2,4,10,11,33)予以保留.但在后面处理过程中，这棵子树的左右孩子，即叶节点数分别为3和2的两棵子子树符合剪枝处理条件，最终只有(11，2)两个叶节点予以保留，其余三个叶节点(4,10,33)被剪枝删除.这个过程体现了最大限度保留原始样本点空间形态这一思想.

图4 Reduce-tree实例Fig.4 Reduce-tree instance

图5 Pruned-tree实例Fig.5 Pruned-tree instance

表3 剪枝处理过程实例Table 3 Examples of pruning process

3.2 利用“双树”结构查找K近邻

本文提出的“双树”结构K近邻搜索方法需要调用原始Ball-tree结构K近邻搜索算法，但是需要对原始算法进行两点改进，改进算法名为search_KNN_Improve，传入参数与原始算法相同.第一点改进是原始算法中KNN_result数组初始值为空，改进算法的KNN_result数组初始预置一个近邻值，这个近邻值是待查点target在剪枝树中定位的一个近邻值.第二点是对原始算法的Step 3进行了改造，原始算法是当KNN_result数组元素个数不足K个时，会尽快将其补充为K个，这容易导致KNN_result数组初始K个元素值过大，剪枝效果差.改造之后不再强制要求KNN_result数组必须达到K个元素，由于KNN_result数组元素按照空间距离值distance降序排列，只要当前处理样本点与待查点target的空间距离值小于KNN_result[0].distance，即将当前数据点加入KNN_result数组，当数组元素个数大于K时，将KNN_result[0]元素删除，更新之后仍然保证KNN_result数组元素按照distance值降序排列.如果KNN_result数组中初始近邻值略大于待查点的第K个近邻值，将产生最佳的剪枝效果，如果初始近邻值设置过小，算法最终运行之后，KNN_result中元素个数可能不足K个.因此如何确定KNN_result数组中的初始近邻值以产生最佳的剪枝效果是一个关键问题.

基于“双树”结构的K近邻搜索算法3的基本思想是先在剪枝树内调用原始K近邻算法search_KNN()查找待查点target的K_g个近邻点，其中1≤K_g≤K.之后分别用第1个和第K_g个近邻点作为被删树的初始近邻点，调用改进算法search_KNN_improve()在被删树内查找target的K个近邻点，如找到的近邻个数不足K个，则将最近邻数组置空，调用原始算法search_KNN()在Ball-tree结构内查找target的K个近邻点.通过算法4确定K_g的最佳值，使得绝大部分待查点在剪枝树和被删树内即可找到K个最近邻，同时由于设置了初始近邻点，查询过程中，将有更多分枝被剪枝过滤，查询速度进一步提高.

“双树”结构K近邻递归搜索算法3：search_KNN_IN_double_tree(ball_tree,pruned_tree,reduce_tree,target,K,K_g)：

输入参数：原始ball_tree根节点；被删树pruned_tree根节点；剪枝树reduce_tree根节点；待查点target；待查最近邻个数K；剪枝树内待查最近邻个数K_g.

输出参数：待查点的K个最近邻数据点.

Step 1.调用原始单树结构K近邻搜索算法reduce_tree.search_KNN()，确定待查点target在剪枝树内的K_g个近邻点，找到的K_g个近邻点存储在reduce_tree.KNN_result数组内.

Step 2.将待查点在剪枝树内的最近邻点预置到被删除树的K近邻数组内，即执行pruned_tree.KNN_result[0]=reduce_tree.KNN_result[K_g-1].调用改进的单树结构K近邻搜索算法pruned_tree.search_KNN_improve()，确定待查点target在被删树内的K个近邻点.此时的剪枝约束条件较为严格，如果定位的近邻点个数num>=K，则算法结束，否则执行Step 3.

Step 3.将待查点在剪枝树内的“最远”近邻点预置到被删树的K近邻数组内，即执行pruned_tree.KNN_result[0]=reduce_tree.KNN_result[0].调用改进的单树结构K近邻搜索算法pruned_tree.search_KNN_improve()，确定待查点target在被删树内的K个近邻点.此时的剪枝约束条件较为宽松，如果定位的近邻点个数num>=K，则算法结束，否则执行Step 4.

Step 4.将完整树的K近邻数组预置为空，使用原始的单树结构K近邻搜索算法在完整树内查找K近邻点ball_tree.search_KNN()，算法结束.

表4 基于“双树”的K近邻搜索实例Table 4 KNN search instance based on “double tree”

表4显示了在图4、图5所示“双树”结构内的5近邻搜索实例.待查点target在二维空间内的位置是(66,212),采用原始Ball-tree结构K近邻算法时，仅有10个叶节点被剪枝过滤，经过与34个叶节点计算比较空间距离，才完成5近邻搜索，查询效率较低.采用“双树”结构K近邻算法后，在剪枝树内经过与10个叶节点比较空间距离，确定剪枝树内的3个近邻点，将待查点与编号36叶节点的空间距离24.08设置为被删树的初始近邻值，而原始算法的初始近邻值为238.13(见表2)，“双树”结构的初始近邻值更接近待查点的第5个近邻点，有更好的剪枝效果，在被删树内经过7次比较，即确定5近邻点.整个查询过程计算比较了17个叶节点的空间距离，共有27个叶节点被剪枝滤除，与原始算法相比，查询效率得到明显提升.实验结果表明剪枝数max_points和剪枝树内近邻点个数K_g对整体查询效率影响很大，例如max_points取值区间为[2,11]，K_g的取值区间为[2,5]，则共可得到10×10=100组可选参数，不同参数的查询效率差别很大，算法4用于确定最优查询参数.

3.3 确定最优查询参数

将原始数据集按照8∶2比例划分，随机选择20%数据点作为测试集，随机性保证测试数据点分布比较均匀，其余80%数据点作为训练集.利用随机算法，共生成10组测试和训练数据集，对每组数据集得到的最优参数计算平均值，作为最终的最优参数值.

确定最优查询参数算法4：determine_optimal_parameters(node_density,train_data,test_data,K,max_len)：

输入参数：用于训练的数据点集合train_data；用于测试的数据点集合test_data；存储每棵子树统计信息的node_density数组；待查最近邻个数K；max_len定义剪枝数上限值.

输出参数：最佳剪枝数max_points；最佳剪枝树的近邻点个数K_g；起始近邻点begin_point；结束近邻点end_point；

Step 1.按照train_data集合构成Ball-tree结构；定义实数变量T1、T2，初值均为0，这两个变量用于时间统计；定义整数变量Len，初值为2.

Step 2.按照train_data集合，调用算法2构造剪枝树(reduce-tree)和被删树(pruned-tree)，剪枝数设定为Len.定义整数变量i，初值为1.

Step 3.如果i<=len(test_data)，执行Step 4，否则，令Len=Len+ 1，如果Len

Step 4.定义整数变量j，初值为2.如果j<=K，执行Step 5，否则令i=i+1，执行Step 3.

Step 5.调用search_KNN_Improve(KNN_result,reduce-tree,test_data[i],j)，查询test_data[i]在剪枝树中的j个近邻点，T1为查询消耗的时间.

Step 6.定义整数变量n，初值为1.如果n<=j-1，执行Step 7，否则，令j=j+1，如果j<=K，执行Step 5，否则令i=i+1，执行Step 3.

Step 7.令begin_point_=n，end_point_=j，调用算法3查询test_data[i]在“双树”结构内的K近邻点，限定剪枝树内查询的近邻点个数K_g=j，限定被删树的两个初始近邻点为reduce_tree.KNN_result[j-1]和reduce_tree.KNN_result[n-1]，T2为这步查询所消耗的时间.调用update_into_result(Len,j,begin_pos,end_pos,T1+T2);统计每种查询参数消耗的查询时间，result数组元素结构为[max_points_,K_g_,begin_point_,end_point_,T_]，其中前四项为主关键字字段，如果result数组中没有对应的记录，则新增，否则将T1+T2值追加到相应记录.令n=n+1，如果n<=j-1，执行Step 7，否则，令j=j+1，如果j<=K，执行Step 5，否则令i=i+1，执行Step 3.

Step 8.调用Sort_result_by_desc(result,T);按照时间统计结果，升序排列result数组元素，排序之后result[0]元素各字段值即为最优参数值.

图6 最佳查询参数统计Fig.6 Best query parameter statistics

对图3(a)所示二维空间内3960个样本点按照8∶2比例划分训练和测试集，待查找的近邻数K为5，将剪枝数范围限定为[6,29]，将剪枝树近邻点个数K_g限定为[2,5]，利用算法4得到的最优参数如图6所示，对10组训练和测试结果计算均值后，得到最优max_points=14，最优K_g=2，在这组参数作用下，全部测试点平均查询时间为3.2秒；同时得到最差参数为max_points=6，最差K_g=2，使用这组参数，平均查询时间为10.8秒.

图7显示的是在最佳参数和最差参数作用下，对400个测试点与剪枝树起始近邻点距离reduce_min_radius，结束近邻点距离reduce_max_radius和完整树第K个近邻点距离all_max_radius进行了统计分析.图7(a)是按照reduce_min_radius降序排列的最佳参数测试结果，可见在最佳参数作用下，绝大部分测试点与第K个近邻点的距离值all_max_radius小于reduce_min_radius，可在被删树内进行一次检索即可命中K近邻点，只有极少量测试点的all_max_radius大于reduce_max_radius，因此整体查询效率最高.图7(b)是按照all_max_radius降序排列的最差参数测试结果，可见在最差参数作用下，绝大部分测试点与第K个近邻点的距离值all_max_radius大于reduce_min_radius，但是小于reduce_max_radius，即需要两次检索被删树才能确定K近邻点，极个别测试点需要检索完整树才能确定K近邻.

图7 400个查询点近邻距离统计Fig.7 Neighbor distance of 400 query points

4 实验测试分析

实验测试采用的软、硬件配置如下，设备型号：ThinkPad P1隐士，CPU：i7-9850H，运行内存：32GB，硬盘容量2TB，操作系统：Windows 10.全部实验数据来自UCI数据集，UCI数据集目前共有507个样本集合，被广泛应用于各类机器学习研究工作.本文选取8个样本集合，如表5所示，样本集涵盖了多种特征维度和样本数量，将每个样本集中非数值型字段(例如月份、星期)，统一转换为数值型字段，并对数据进行归一化处理，即将全部属性值映射到[0,1]区间.对每个样本集合按照8∶2的比例划分训练和测试集.为了保证数据分布比较均匀，采用随机方式选取数据，对每个样本集进10次实验，将10次测试结果的均值作为最终实验数据，搜索的最近邻个数统一设置为5.

表5显示在8个样本集上，分别应用基于Ball-tree结构的原始KNN算法和基于“双树”结构的改进KNN算法进行测试.实验结果表明，原始KNN算法在维度较低、样本数较少情况下，表现良好.随着特征维度和样本数增加，查询所消耗时间显著增长，针对维度为10、样本数为58000的Shuttle集合，查询时间达到13271.605秒，针对维度为2400，样本数为8320的Swarm集合，处理时间也达到1203.062秒.这样的处理速度很难满足实时性要求高的任务需求，如网络攻击在线实时检测.

表5 实验结果比较Table 5 Comparison of experimental results

使用基于“双树”的改进KNN算法对8个样本集进行查询处理，在特征维度和样本数量显著增加条件下，查询时间并未急速增长.针对Shuttle集合，改进算法查询时间为836.057秒，比原始算法节省12435.548秒，增速达到93.7%.针对Harus集合，改进算法用时18.796秒，增速达93.2%.分析如下，在改进算法中，通过统计分析得到最优“双树”构造参数，利用最优参数构建剪枝树和被删树具有最小的剪枝半径，可以达到最佳剪枝效果，有更多的数据点在查询过程中被剪枝删除，整体计算量减少，查询效率显著提高.同时由于最优参数也是基于原始样本集按照8∶2比例划分训练和测试集统计得出，因此在此基础上得到的查询统计时间整体表现良好，当测试集来自不同集合时，即测试集不从样本集中选择时，整体查询性能略有下降，但仍维持较高增速.

5 结 语

本文提出一种“双树”构造方法，可以从原始样本集构建剪枝树和被删树.由于对原始样本集内高密度区域和离群点区域进行了区分处理，构建的剪枝树包含尽可能少的样本点，且最大限度地保留了原始样本集在高维空间的分布形态.与基于Ball-tree结构的K近邻查找算法相比，本文提出的“双树”结构K近邻搜索算法解决了因初始近邻点位置固定，导致的剪枝半径过大，查询效率较低问题.改进算法的初始近邻点动态分布于待查点附近，有效缩短了剪枝距离，在查询过程中，有更多的样本点被剪枝滤除，计算量显著减少，查询效率明显提高.实验结果表明，与原始算法相比，改进算法在处理高维、海量样本集时仍维持较高增速比.

受样本集在多维空间分布形态影响，构建的剪枝树和被删树可能存在不平衡问题.下一步计划研究基于PCA(Principal Component Analysis)的空间划分方法，以构建相对平衡的二叉树结构，进一步改进、提升K近邻查询效率.