复式钢管混凝土柱轴压承载力手算方法与有限元法对比分析

姚荣康

（广东省建筑设计研究院有限公司，广东广州 510010）

0 引言

复式钢管混凝土柱是一种新颖的组合构件，内外两根钢管里外同心放置，并全部内填混凝土而形成的。对比单钢管混凝土柱，复式钢管混凝土柱的优点有下述四点：①钢管壁较薄；②加强层伸臂桁架与钢管混凝土柱的连接构造简单；③减小了混凝土的径向收缩量；④耐火安全性提高。在外钢管因火灾软化时内层钢管仍能继续承担荷载。因此复式钢管混凝土柱在超高层建筑中有宽广的使用场景[1]。目前，复式钢管混凝土柱的手算方法主要有三种，分别是极限平衡理论方法、统一理论方法及高层建筑结构混凝土技术规程（简称《高规》）建议的方法。

1 复式钢管混凝土柱轴压承载力手算方法

1.1 手算方法一：基于极限平衡理论

根据极限平衡理论[2]的叠加原则，当计算里层钢管内部的混凝土强度时，内外层钢管的套箍作用均需考虑。对于外圆内圆的复式混凝土柱截面，其轴压承载力计算公式为：

式中：η-钢管叠加折减系数，一般取0.9；φl-长细比影响折减系数分别为内外层钢管之间的套箍混凝土极限强度。

1.2 手算方法二：基于统一理论

张志权[3]参照钢管混凝土统一理论，综合论证内外钢管使用不同钢材的截面形式，不区分钢与混凝土两种材料，提出一个计算基本参数：组合等效套箍系数，并将其应用在轴压承载力计算上。对于圆形截面，其内部混凝土的套箍系数ξ 可表示为：

式中：As、Ac分别为钢管和混凝土面积；fs-钢材受压强度标准值、fck-混凝土抗压强度标准值。

根据统一理论可以知道，钢管混凝土柱无须对不同形式的截面采用不同的公式计算，只需采用统一的轴心受压承载力公式，则有：

1.3 手算方法三：《高规》建议的计算方法

我国《高规》F.1.2 中，对于钢管混凝土单肢柱的轴压承载力设计值，有如下计算公式：

式中：θ=Aafa/Acfc-钢管混凝土的套箍指标；[θ]-套箍指标的界限值；其余参数详见《高规》。

2 计算算例

某复式钢管混凝土柱钢管采用Q345B 等级钢材，混凝土等级为C50，外钢管外径为406mm，内钢管外径为219mm，该柱长度为3500mm，内外钢管壁厚分别为8mm、9mm、10mm，共九种截面。

2.1 计算方法一：基于极限平衡理论

以内外钢管壁厚均为8mm 为例列出详细计算过程：

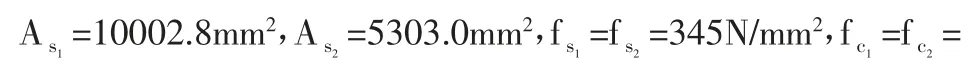
表1 不同计算方式计算复式钢管混凝土柱承载力

2.2 计算方法二：基于统一理论

同样以内外钢管壁厚均为8mm 为例列出详细计算过程：

2.3 计算方法三：《高规》附F.1.2 建议公式

同样以内外钢管壁厚均为8mm 为例列出详细计算过程：

2.4 计算方法四：采用有限元软件进行计算

2.4.1 材料本构选取

钢材的本构关系定为双折线，其达到强化阶段后，弹性模量取为0.01Es，泊松比取为0.2。混凝土本构模型则使用塑性损伤模型，曲线采用《混凝土结构设计规范》中推荐的曲线。

2.4.2 有限元模型单元类型选取及界面相互作用

钢管使用四节点线性壳单元模拟，混凝土使用八节点线性实体单元模拟。钢管和混凝土的法向使用硬接触，切向使用库仑摩擦接触，摩擦系数为0.6。模型底部定义固接约束，模型顶部采用位移加载（竖直向下50mm）。

2.4.3 有限元分析荷载位移曲线

更改壁厚分别对有限元模型进行分析，得到复式钢管混凝土柱的荷载—位移曲线，如图1 所示。

图1 荷载—位移曲线

2.5 计算结构汇总及对比

用四种方法计算得到九个截面的承载能力汇总如表1 所示。

从表1 可以看出，用三种手算方式计算得到的复式钢管混凝土柱轴心受压承载力均比有限元分析结果小；采用极限平衡理论和统一理论计算的复式钢管混凝土柱轴心受压承载力结果差别很小，在5%以内，随着壁厚增加两种方法计算的承载力差别也有所增大，总的来说用极限平衡理论计算比用统一理论计算的要大；而采用高规建议方法计算到的结果比其他两种计算结果都要小，偏于保守。

3 结语

本文通过对比四种计算结果，可以得出：采用高规建议方法计算最保守，采用极限平衡理论计算的结果比采用统一理论计算的结果稍大，这三种方法计算的轴压承载力都比有限元分析得到的结果要小，其原因可能为三种方法考虑了截面设计的各种不利因素，对截面设计时设置了一定的富余量。