基于线性二次滚动时域法的运载火箭发动机推力故障诊断

叶 松，陈 曦，熊寸平

(北京航天自动控制研究所，北京 100854)

0 引言

随着航空航天技术的快速发展，运载火箭的组成越来越复杂，其可靠性和安全性问题日益突出[1]。故障诊断技术的应用，能够及时检测系统故障，提高系统的可靠性，同时为后续容错控制奠定基础。动力系统作为运载火箭的一个关键系统，为运载火箭提供动力，推动运载火箭前进。推力下降故障是动力系统故障类型之一，会导致系统性能退化甚至不稳定，因此研究推力下降故障诊断具有重要意义。

故障诊断包含故障检测、估计与故障定位。故障检测反映故障的发生，故障估计表征故障程度，故障定位表征故障发生的位置。故障诊断常用基于动态模型的方法[2-3]、基于信号处理[4-5]的方法以及基于知识[6-7]的方法。基于成熟的运载火箭建模理论，采用基于动态模型的方法更具有工程应用价值。

基于动态模型的非线性系统故障诊断方法主要有状态估计法、参数估计法。前者通常对非线性模型的某些特征点进行线性化，利用建模误差作为未知输入并设计未知输入观测器获取残差，进行故障诊断，后者通常对非线性模型利用非线性参数估计的方法进行故障诊断。王青等[8]采用状态估计法，基于线性化后的飞行器模型，设计降阶故障检测滤波器，在减少计算量的同时保证了故障检测的快速性。符文星等[9]研究了基于强跟踪滤波器的参数估计方法，对运载火箭的推力参数进行了正确估计。

本文结合状态估计法与参数估计法，提出了一种基于扩展卡尔曼滤波器生成残差，采用线性二次滚动时域算法[10]估计故障，并根据过载方向定位故障的方法，对发动机推力下降故障进行在线检测与定位。最后将该方法进行数学仿真，验证了算法的有效性。

1 数学模型

本文以运载火箭为例，火箭动力系统包含4台摇摆发动机，其布局如图1所示。

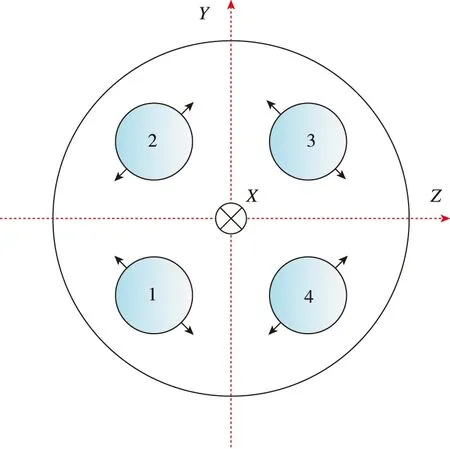
图1 火箭发动机布局图Fig.1 Distribution of launch vehicle power system

受地球自转的影响，发射坐标系为动坐标系，这样存在附加哥氏力和力矩、附加相对力和力矩的影响，但本方法中这些影响均可以视作滤波器噪声，因此将发射坐标系视作惯性系，从而忽略附加哥氏力和力矩、附加相对力和力矩的影响，以突出研究的重点。简化后的运载火箭动力学及运动学方程[11]

(1)

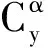
(2)

(3)

式中，γ为滚转角，ϑ为俯仰角，ψ为偏航角。

取状态变量如下

(4)

记

可得

(5)

为简化计算，取量测变量为除发动机推力外的12个状态变量

yi=xi+vi

(6)

式中，i=1,2,…,12。v为白噪声序列。

上述模型进行线性化和离散化并写为如下非线性形式

x(k+1)=F(k,u(k),x(k))+Γ(k)v(k)

y(k+1)=H(k+1,x(k+1))+e(k+1)

(7)

式中，整数k≥0为离散时间变量，x为状态变量，u为输入向量，y为输出变量。非线性函数F，H为状态的一阶连续偏导数，Γ为已知矩阵。系统噪声v(k)、测量噪声e(k)为高斯白噪声，互不相关。在此基础上，设计扩展状态观测器(Extended Kalman Filter，EKF)如下

X(k+1)=X(k+1,k)+K(k+1)[Z(k+

1)-H(k+1)X(k+1,k)]

(8)

滤波增益阵K为

K(k+1)=P(k+1,k)HT(k+1)·

1)+R(k+1)]-1

(9)

预报误差协方差阵为

P(k+1,k)=Φ(k+1,k)P(k)ΦT(k+

1,k)+Q(k)

(10)

状态估计误差协方差阵为

P(k+1)=[I-K(k+1)H(k+1)]P(k+1,k)·
[I-K(k+1)H(k+1)]T+
K(k+1)R(k+1)K(k+1)T

(11)

式中,X(k+1,k)为状态的一步预测值如下

X(k+1,k)=f(X(t))|X(t)=X(tk)

(12)

Φ(k+1,k)为状态转移矩阵如下

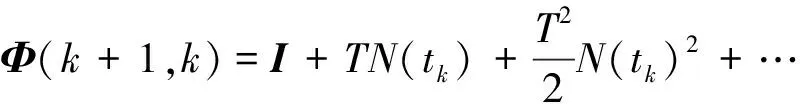
(13)

H(k+1)为量测转移矩阵，根据状态变量和量测变量的关系，可以得到H(k+1)为单位阵。

“我上一次到访查谟-克什米尔大君的斯里那加宫殿时， 他们端出了三十个盘子，如果我说任何一个盘子上的宝石都能在市场卖得到一百万元，恐怕是远远低估了这些宝物的美及它所代表的财富。”

将模型实时观测到的某状态量与EKF方法下状态量的计算值作比较，可得到系统残差预测向量

(14)

式中,r为1×n维。

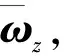
(15)

式中,rωz为1×n维。

2 故障诊断算法设计

考虑运载火箭推力下降故障，记推力下降程度为f，f∈(0,1)，0表示推力下降程度为0%，1表示推力下降程度为100%。当发动机发生推力故障时，推力Pf如下

Pf=(1-f)P

(16)

2.1 残差表示

残差数据Y为某个时间间隔内残差向量rωz的采样值，以如下形式表示

(17)

式中，tb为数据采样开始的时间，Δ为采样间隔，N为样本的数量，f为故障程度。向量Y的大小为(N+1)×1。

2.2 灵敏度矩阵求解

假定动力系统运行正常，则零故障记为Y(tb,N,Δ;0)；若发生故障，获得的残差数据将进一步表示为Y(tb,N,Δ;f)。将故障残差数据线性化处理，分为无故障残差部分和故障相关部分，如下

Y(tb,N,Δ;f)≈Y(tb,N,Δ;0)+S(tb,N,Δ)f

(18)

式中，S为关于Y(tb,N,Δ;f)的最后一个参数f的(N+1)×1雅可比矩阵，称为灵敏度矩阵。

(19)

无故障情况下的残差为

r0(t)=r(t;f=0)

(20)

由于实际中残差无法直接对故障求导，可通过下式求解灵敏度矩阵参数

(21)

式中，d是有限差分步长，与采样时间保持一致。e为单位故障向量，表征1%的推力下降程度。通过下式对特征数据进行采样来计算矩阵S。

(22)

2.3 估算算法

前文介绍了残差向量Y以及灵敏度矩阵S的求解，下文对故障估算算法进行介绍。

对于实际系统，由于传感器噪声和建模误差的存在，残差不为零。将所有这些因素汇总在一个广义的“噪声”ew数据向量中。假设残差数据向量Y的统计模型如下

Y=Sf+ew

(23)

通过对该残差数据模型中的变量进行统计假设，可以得出故障参数的估计值。一种设计方法是将统计参数视为估算算法的调整参数，可以对这些参数进行调整，以实现算法的合理实用性能。基于此，假设噪声ew是具有协方差矩阵V的正态分布向量。同时假定要估计的未知故障向量f是独立于(噪声ew)的随机变量，并且为具有协方差矩阵R的正态分布向量。在这种情况下，可以从噪声数据中获得故障向量f的最佳统计估计值

(24)

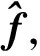
在此过程中如果忽略传感器噪声，唯一建模误差是残差与故障矢量关系式中一阶近似的线性化误差。在实施估计算法时，协方差矩阵V设为单位矩阵，这对应于所有观察通道中存在的相同幅度的白噪声。

将故障的协方差矩阵R选择为

R=F2

(25)

F具有预期故障强度的含义。可以基于故障性质的知识来设置故障强度，实际中通过多次测试获取。

故障向量可以从整个飞行过程中收集的数据集作为一个批处理估计获得，但是，可能需要在整个飞行过程中计算和更新估算值，以便在线估算和观察不断发展的故障。为满足此需求，以滚动时域的形式实现用于故障参数估计的GLS算法。在每个时间步，滚动时域算法使用N个最新数据点来计算故障参数矢量的估计值。此估算形式如下

(26)

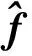
由于一种故障类型对应一种故障强度，因此针对单一的推力下降故障，故障协方差阵维数恒为1×1。因此选用单一残差向量ωz保证公式(25)的维数匹配，满足对故障敏感的残差均可选用。

2.4 故障定位

基于残差信息的故障检测仅能反映整体的故障时刻以及故障程度，当4台发动机的某一台发生故障时，仅基于残差无法区分4台发动机的故障信息。因此提出一种基于故障时刻的过载方向信息定位故障的方法。进行仿真分析，当动力系统4台发动机分别在25 s发生30%推力下降故障时，ny(箭体系y1方向过载),nz(箭体系z1方向过载)状态如图2、图3所示。

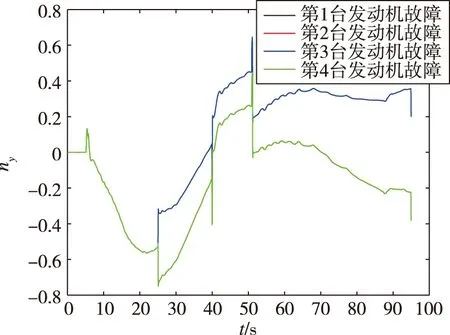
图2 4台发动机分别故障下过载ny响应曲线Fig.2 ny response with each individual engine fault

图3 4台发动机分别故障下过载nz响应曲线Fig.3 nz response with each individual engine fault

由图2、图3可以得知，过载ny在第2，3台发动机故障响应相似，第1，4台发动机故障响应相似。过载nz的第1，2台发动机故障响应相似，第3，4台发动机故障响应相似。因此检测出故障发生后，可根据ny，nz的突变方向，综合判定故障发动机的编号。利用这种特性，可以应用于故障检测方法中。

2.5 算法流程

提出的方法分为生成残差、估计算法与故障定位3部分。

第1部分在推力无故障情况下，以P，vx，vy，vz，ωx，ωy，ωz，x，y，z，φ，ψ，γ作为输入数据，基于预测模型，利用EKF方法得到除推力P外的预测数据计算值，计算残差。

由上述状态量计算的残差不能完全反映推力下降故障，通过分析残差数据vx，vy，vz，ωx，ωy，ωz,x,y,z,φ,Ψ,γ的曲线发现，推力下降故障仅对vx，vy，vz，ωx，ωy，ωz影响非常比较明显。其中，vy，ωy与ωz在某些时刻的残差有明显突变，且故障后一段时间能够将系统控制到稳定状态，符合实际情况，因此采用ωz计算残差。

将无故障的状态参数ωz与预测值做差，即得到残差r0。同理，在1%故障下ωz实际值与预测值做差对应生成残差rf_1%。

在推力故障情况下，通过推力P，由EKF计算故障下的状态参数ωz，最终生成rf。

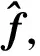
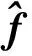
3 仿真分析

3.1 单台分析

(1)不同采样长度N对仿真结果的影响

设定50 s时发生50%的推力下降，考虑到控制器在10 ms左右即可控制住故障，采样长度N分别为1，5，10，采样间隔Δ为0.01 s,协方差阵R=202,将历史缓冲区取NΔ对应值，分别为0.01，0.05，0.1 s，仿真结果如图5、图6所示。

由图5、图6可以看出，采样长度N越大，故障估计值f恢复正常的拍数越少，越不利于观测到故障；采样长度过小，故障估计值f有较大损失。为了保证故障检测的及时性及准确性，采样长度为5较为合适，实际应用中可根据此分析方法确定实际采样长度。

图4 估算算法流程图Fig.4 Flow chart of estimation algorithm

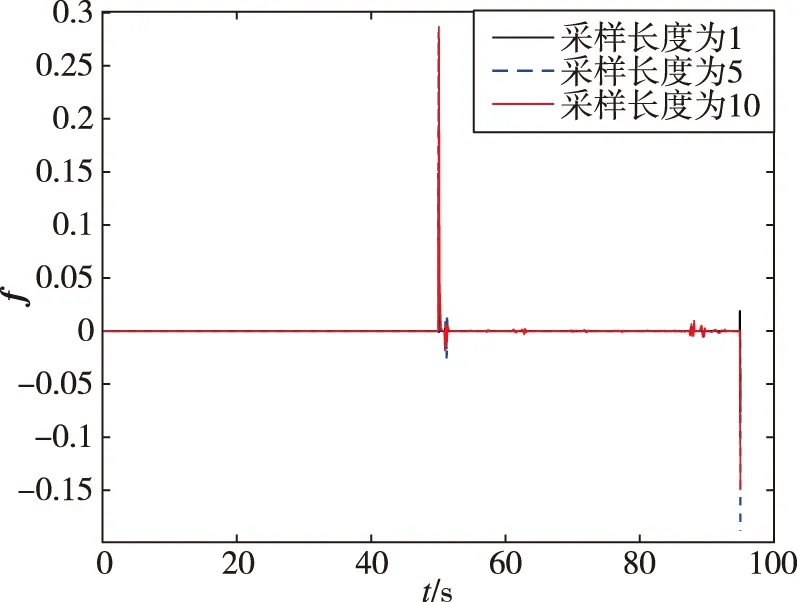
图5 不同采样长度下故障检测结果Fig.5 Fault detection results under different sampling lengths

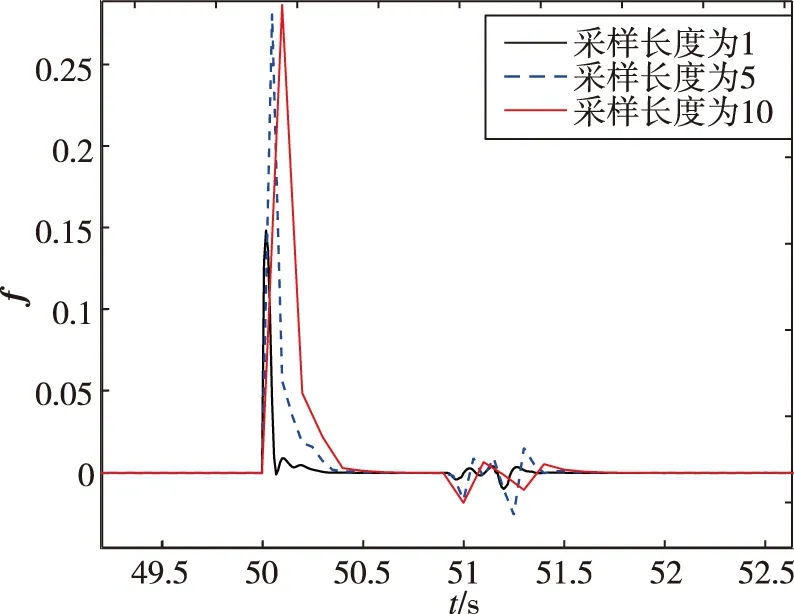
图6 不同采样长度下故障检测结果放大图Fig.6 Enlarged view of fault detection results under different sampling lengths

(2)不同故障协方差矩阵R对仿真结果的影响

设定50 s时发生50%的推力下降，采样长度N为5，采样间隔Δ为0.01 s,协方差阵R分别为0.012，12，202，5002，5 0002，10 0002,历史缓冲区为0.05 s，图7给出50 s附近故障估计结果。

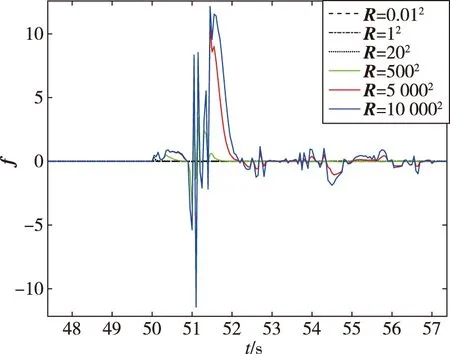
图7 50 s附近不同协方差阵下的故障估计结果(大范围)Fig.7 Fault detection results under different covariance matrices around 50 s(wide range)

由图7可以看出，协方差阵取得越大，f反映故障发生强度越显著，但取得过大f会出现二次增大，可能导致故障检测的误报。根据上述结果进一步确定合适的协方差阵大小，协方差阵R分别为12，52，202，502，1002,仿真结果如图8所示。

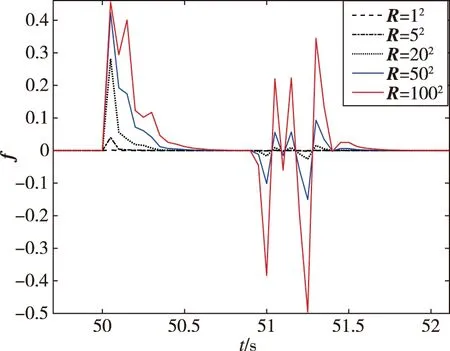
图8 50 s附近不同协方差阵下的故障估计结果(小范围)Fig.8 Fault detection estimation results under different covariance matrices around 50 s(small scale)

考虑到故障检测的准确度，避免二次误报，因此选取R=202至502量级较为合适。

(3)不同推力下降程度仿真

基于上述仿真，给出同一时刻(20 s)下，推力下降故障分别为0%、30%、50%时的仿真结果，取采样长度N=5，采样间隔Δ为0.01 s,协方差阵R=202,将前0.05 s数据作为历史缓冲区，故障残差仿真结果如图9、图10所示，故障向量f的估计如图11所示。

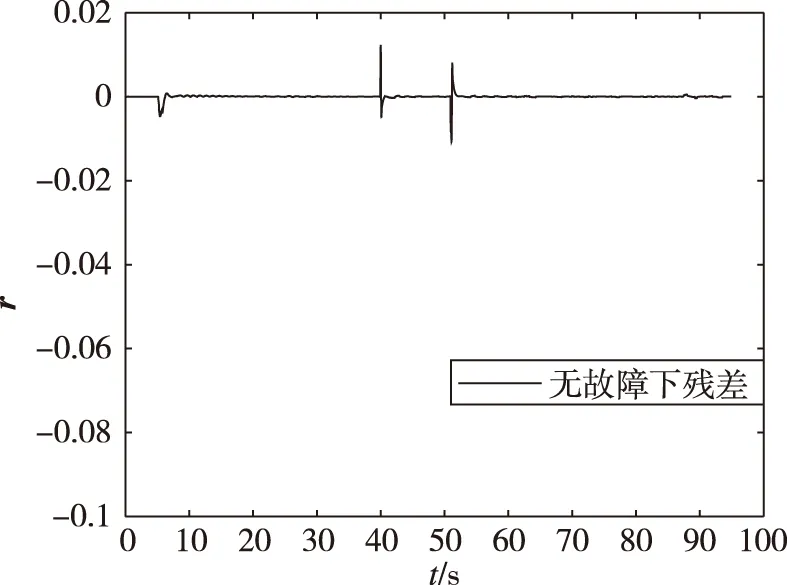
(a) 无故障

(c) 50%故障图9 20 s时刻不同故障程度残差仿真结果Fig.9 Simulation results of residuals with different fault degrees at 20 s

(a) 无故障

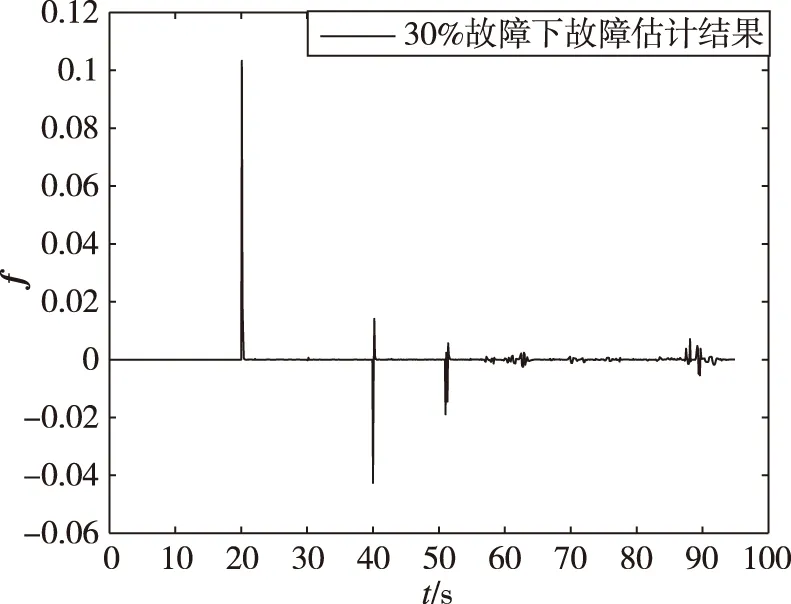
(b) 30%故障

(c) 50%故障图10 20 s时刻不同故障程度故障检测仿真结果Fig.10 Simulation results of fault detection with different fault degrees at 20 s

由上述结果可得，同一时刻发生不同故障程度，f估计值不同。在20 s时刻，以5%故障下降程度为间隔，仿真获取故障时刻估计的峰值为fmax，绘制曲线如图11所示，可以判断两者存在近似的线性关系。

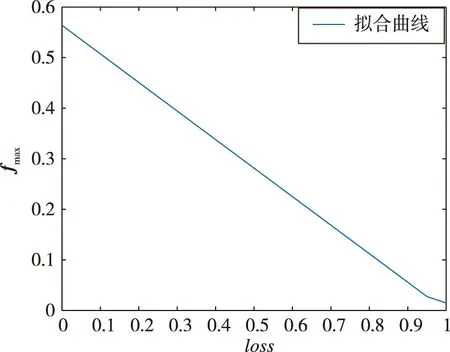
图11 故障程度与故障估计值f关系Fig.11 Relationship between fault degree and fault estiomate f

由图11可以看出,两者之间存在线性关系，由于该曲线仅针对50 s时刻故障，遍历时间与故障程度，形成一个二维表格，根据辨识结果在表格内进行插值，即可得到推力下降程度。

以推力下降程度lossP为因变量、f估计峰值为自变量进行线性拟合，可得到20 s时刻下估计值f与实际推力下降程度lossP关系式

(27)

利用上式将故障估计值与预设的故障程度对应，表1给出部分验证结果。

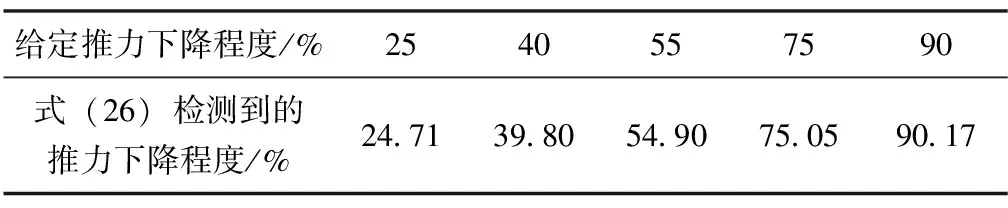
表1 故障程度的估计结果

上述结果表明，该方法能够较为准确地获得故障损失程度。在检测出故障后，由于控制器的控制作用，所以突变恢复正常。残差曲线中40，50 s附近也产生了与推力下降故障不相关的突变。由表1可以看出，这些突变造成的f估计值的变化远小于推力下降故障造成的估计结果的变化，表明该方法对推力下降故障具有较高的灵敏度。

3.2 4台发动机故障检测

基于过载在故障时刻突变方向与发动机位置相关的思路进行多次故障检测验证，结果如表2所示。

表2 故障发动机编号检测

上述结果表明，利用根据ny,nz的突变方向能够准确判定发动机故障台的编号,表明该思路能够用于4台发动机的故障定位。

4 结论

本文针对运载火箭动力系统的推力下降故障，提出了一种线性二次滚动时域算法用于估计故障时间与故障程度，结合估计算法检测的故障时间提出一种故障定位的策略。仿真结果表明，该方法能够成功检测发动机故障，并对该类型故障具有较高灵敏度。

此外，给出根据过载的突变方向定位故障的策略，与估计算法检测的故障时间相结合，实现了发动机故障的准确定位。