上面级发射MEO轨道设计及运载能力优化研究

王传魁，焉 彬，张利宾，郑莉莉，陈佳晔，周文勇，陈 益

(北京宇航系统工程研究所，北京 100076)

0 引言

运载火箭可以较容易地直接将卫星送入LEO(Low Earth Orbit)、SSO(Sun-Synchronous Orbit)等低地球轨道，但对于高度在10 000 km以上的中高轨道，受运载火箭末级多起启动能力的限制，一般无法采用直接入轨的方式进行发射。以往进行中高轨道卫星发射时，一般采用间接入轨的方式，由卫星在远地点开展一次或数次变轨机动进入最终轨道。上面级的出现进一步提升中高轨道卫星的发射能力，可以将卫星直接送入中地球轨道(Medium Earth Orbit，MEO)和地球静止轨道等中高轨道[1]。

中地球轨道MEO主要用于导航卫星星座轨道，例如美国的GPS导航星座、俄罗斯的GLONASS导航星座、欧洲的Galileo导航星座和我国的北斗导航星座等。为避开地球辐射带,增大覆盖范围,减少卫星数量，MEO轨道一般选择高度位于20 000～24 000 km、轨道倾角在55°～65°的圆轨道[2]。

我国设计的导航星座中，工作在MEO轨道的导航卫星不少于24颗[3]，其工作轨道高度约为21 500 km，轨道倾角为55°。为加快全球卫星导航系统的建设，尽快提供导航服务，我国导航卫星组网阶段，MEO卫星均采用上面级以一箭双星直接入轨的方式进行发射，上面级可以将卫星送入约22 000 km高度的组网调相轨道，卫星分离后自主调相至各自的工作相位，以便尽快完成星座部署任务。为提升发射轨道运载能力，将更多的导航卫星有效载荷送入MEO轨道，需要开展发射轨道运载能力优化研究，这对加快北斗卫星导航系统组网进程、高效完成北斗卫星导航系统工程建设具有重要意义[4]。

郦苏丹等[5]以区域目标覆盖性能为优化指标，采用多目标进化NSGA-Ⅱ算法对较低的MEO轨道进行优化，得到5颗MEO椭圆轨道卫星星座方案。蒙波等[6]以导航星座性能PDOP和简化计算的卫星生产成本为目标，采用多目标PSO优化算法对导航星座轨道面个数、卫星总数量、星座轨道相位因子以及轨道倾角等参数进行了优化。赵双等[7]以导航星座失效为背景，提出发射快速相应卫星进行星座重构的方法，并以重构后星座对目标区域的平均 GDOP值和相应时间为目标，采用多目标进化NSGA-II算法对卫星数量、发射点位置以及卫星入轨半长轴、轨道倾角和升交点赤经进行了优化。

以上研究均针对导航组网星座卫星轨道进行了优化，实现了星座优化的效果，但尚未开展对运载火箭或上面级发射导航卫星MEO轨道设计及优化方法研究。本文从上面级两次变轨直接入轨发射MEO轨道设计方法为切入点，建立轨道动力学模型和迭代计算模型，分析影响发射轨道运载能力的可变因素，应用自适应遗传算法进行优化，以期获得发射轨道优化和运载能力提升。

1 轨道设计方法

1.1 发射轨道方案概述

上面级直接入轨发射中高轨道卫星一般采用两次变轨方案，上面级卫星组合体与基础级火箭分离后进入停泊轨道，上面级在停泊轨道完成姿态稳定等动作后主发动机点进行第一次变轨，通过上面级主发动机工作，加速抬高停泊轨道远地点高度使得组合体进入MEO转移轨道(简称MTO轨道)。第二次变轨在MTO轨道远地点进行，目的是抬高轨道近地点以圆化轨道，并修正轨道倾角，最终将卫星送入目标轨道，变轨示意如图1所示。

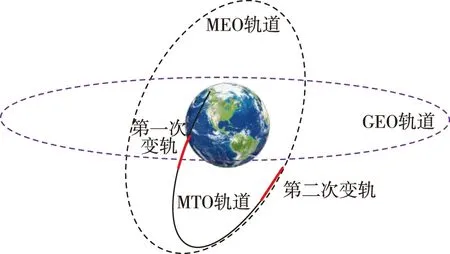
图1 飞行轨道示意图Fig.1 Schematic figure of orbit

1.2 动力学方程

建立在惯性坐标系下的上面级轨道动力学方程可写为如下微分方程的形式

(1)

式中，x，y，z为上面级位置矢量在地心赤道惯性坐标系下的分量，vx，vy，vz为上面级速度矢量在惯性系下的分量，Fx，Fy，Fz为上面级所受合外力F在惯性系下的分量。上面级所受合外力F

F=FT+FE+FA

(2)

式中，FT为上面级主发动机推力，FE为卫星受到的地球引力，FA为高空大气阻力。

1.3 变轨段推力方向设计

结合笔者前期研究成果及方法[8]，变轨段推力方向主要为上面级体系相对轨道系的俯仰角φ、偏航角ψ、滚动角γ的设计，因上面级变轨发动机一般安装于本体X轴向，滚动角对推力方向不产生影响，为简化计算γ按照0°进行计算。因此，变轨段推力方向主要为相对轨道系俯仰角φ和偏航角ψ的设计。为使得变轨发动机尽可能沿速度方向加速，提供最大加速效果，将轨道系俯仰角φ和偏航角ψ按照0°进行设计，考虑到轨道机动还需要修正轨道偏心率和倾角倾角，附加俯仰和偏航小幅修正量δφ和δψ。

1.4 轨道迭代计算

轨道设计采用调整第一次变轨主发动机工作时间t1、第二次变轨主发动机点火时刻t2、第二次变轨主发动机工作时长t3、轨道系俯仰角修正量δφ、轨道系偏航角修正量δψ来最终满足卫星轨道参数，计算上面级第一次变轨后轨道远地点高度Ha1，卫星分离后的弹道倾角Oa、轨道半长轴a、偏心率e、轨道倾角i，采用牛顿迭代算法进行求解，迭代关系式为

(3)

判断上面级第一次变轨轨道远地点高度和卫星入轨参数是否满足如下条件

(4)

上面级第一次变轨后轨道参数主要为轨道远地点高度：Ha1为当前轨道计算MTO轨道远地点高度，Ha1T为上面级第一次变轨结束后的轨道远地点高度目标值(针对中高轨发射任务，一般取值比卫星要求轨道高度高约150 km)，Ha1eps为迭代控制精度(一般取0.01 m)。

卫星入轨参数包括：入轨点当地弹道倾角Oa、轨道半长轴a、轨道偏心率e、轨道倾角i。Oa为当前轨道计算卫星入轨当地弹道倾角；a当前轨道计算时刻卫星入轨轨道半长轴值，aT为卫星要求发射轨道半长轴值，aeps为卫星发射轨道半长轴控制精度(一般取0.01 m)；e为当前轨道计算卫星入轨轨道偏心率；i当前轨道计算时刻卫星入轨轨道倾角，iT为卫星发射轨道的轨道倾角值，ieps为卫星发射轨道倾角控制精度(一般取1×10-5)。其中,Ha1为t1的函数,Oa为t2的函数，a为t3的函数，e为δφ的函数，i为δψ的函数。

2 轨道优化策略分析

2.1 轨道接力能量分配优化

运载火箭三子级采用氢氧低温发动机，相对于上面级来说其优点是比冲高、推力大，适合快速为航天器轨道提速。但因三子级规模较大，将其和上面级组合体一起送入更高的轨道需要更多的燃料。上面级采用常规液体发动机，相对于火箭三子级其比冲稍低、推力较小，但三子级分离后其规模变小，变轨灵活性提升。因此，上面级与基础级火箭交接班轨道条件，特别是过渡轨道远地点高度存在最优解。

2.2 机动段推力方向优化

卫星等航天器一般采用固定姿态推力惯性定向的方式进行变轨段推力方向设计，运载末级火箭一般采用沿飞行轨道速度方向或者线性化飞行程序角的方式进行轨道机动。上面级第一次变轨也可以采用沿速度方向加速，但上面级携带的燃料主要用于第二次变轨，为优化上面级第二次推力方向，避免产生不利方向速度增量增加燃料消耗，上面级第二次变轨段俯仰角采用二次曲线拟合的方式进行优化调整，因基础级火箭直接将上面级组合体送入倾角55°倾角的停泊轨道，用来修正卫星入轨轨道倾角的偏航角数值为小量，优化空间不大。因此，采用优化第二次变轨俯仰角二次曲线中间点的时间和角度值进行优化。

2.3 MTO轨道远地点高度优化

为最大程度地拟合霍曼变轨，上面级第二次变轨段飞行高度也会影响燃料的消耗，上面级采用在MTO轨道远地点附近进行第二次轨道机动的方案，因此MTO轨道远地点高度，即对应第一次变轨结束后的远地点高度，也需要进行优化。

3 优化方法及模型

3.1 优化算法选择

遗传算法是一种借鉴生物界自然选择和遗传机制发展起来的随机搜索优化算法，基于适者生存的原则，通过模拟自然进化在种群内的优胜劣汰实现对最优解的搜索[9]。遗传算法提供了一种求解复杂系统优化问题的通用框架,它不依赖于问题的具体领域,广泛应用于多种学科领域。

基于遗传算法的全局搜索能力，本文将遗传算法应用于上面级发射MEO轨道优化设计，建立目标函数与遗传算法适应度函数的关系，在全局范围内搜索发射轨道优化变量参数的最优解。在影响轨道设计结果参数变量范围内，随机产生初始种群开始最优解迭代搜索，对种群中的个体进行适应度计算，以最大适应度为标准，更新最优适应度和最优染色体，通过选择、交叉和变异等遗传操作生成下一代种群，进行当前种群的个体适应度计算。重复上述步骤，直至找到最优解为止。关于遗传算法的详细操作流程已有研究较多[10]，这里不再赘述。

3.2 轨道优化模型

本文的优化目标选为上面级与卫星组合体进入MEO轨道的质量最大，因最优化问题一般求最小值，所以采用固定质量常数对入轨质量做差，其优化数学模型可以表示为

minJ=MC-M

(5)

式中，MC>0为质量常数，一般取5 000 kg；M>0为上面级和卫星组合体进入MEO轨道后的剩余质量。

根据前文分析，优化变量分别为：运载火箭发射上面级进入停泊轨道远地点高度Ha0、上面级第一次变轨目标轨道远地点高度Ha1、上面级第二次变轨段主发动机工作推力方向二次曲线拟合点时间Tmid及对应的俯仰角ϖmid。使用遗传算法在各变量的取值范围内搜索最优值，在指定的进化代数内，各变量收敛后即可认为找到最优解。

4 仿真算例分析

4.1 仿真计算初始条件

根据我国长征三号乙运载火箭改进型[11]，标准地球同步转移轨道运载能力估算MTO轨道运载能力范围。因此，假设仿真计算采用的火箭上面级主要原始参数如表1所示。初始仿真计算假定按照基础级火箭将上面级送入远地点高度为20 000 km的停泊轨道，停泊轨道主要轨道参数如表2所示，其中近地点幅角和升交点赤经这两项轨道参数的理论取值对MEO轨道运载能力不产生影响，可以随机选取，不再列出。

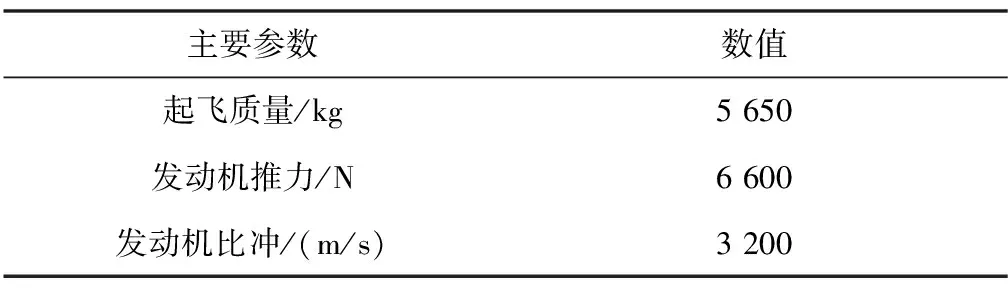
表1 上面级主要性能参数

表2 上面级主要初始轨道参数

4.2 仿真计算结果

根据4.1拟定的初始参数条件，按照1.4节轨道迭代计算方法，一般设定上面级第一次变轨远地点高度目标值为22 150 km，卫星入轨半长轴为28 378.14 km，开展上面级发射MEO轨道迭代计算，计算结果主要参数如表3所示。结果显示，上面级携带卫星组合体最终进入22 000 km高度、55°轨道倾角的圆轨道，计算入轨剩余质量为M0，优化后入轨质量结果采用适应度值进行计算，即适应度值等于优化计算后入轨质量除以M0。

表3 上面级卫星组合体进入MEO轨道后主要轨道参数

4.3 遗传算法优化结果

设置优化计算种群规模为60，最大进化代数为50，交叉率0.8，变异率0.1。参考上述初始计算结果，设定上面级组合体初始停泊轨道远地点高度Ha0的取值范围18 000～21 000 km，并对应估算CZ-3B运载火箭运载能力范围5 800～5 575 kg，在Ha0的取值范围内，假设火箭运载能力小范围内符合线性化规律；设定上面级第一次变轨目标轨道远地点高度Ha1的取值范围22 000～22 200 km；设定上面级第二次变轨段主发动机工作推力方向二次曲线拟合点时间Tmid的取值范围200～450 s，对应点的俯仰角ϖmid取值范围-10°～10°。遗传进化50代后各变量参数变化如图2所示，目标适应度变化情况如图3所示。

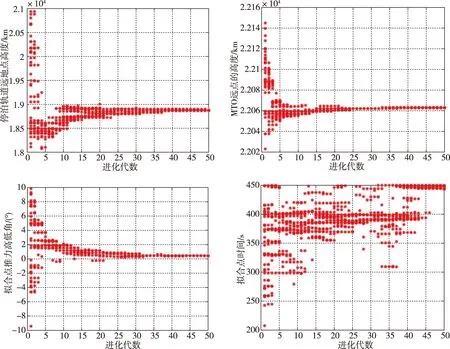
图2 进化50代后种群参数变化示意图Fig.2 Schematic of population variable parameters after fifty generations of evolution

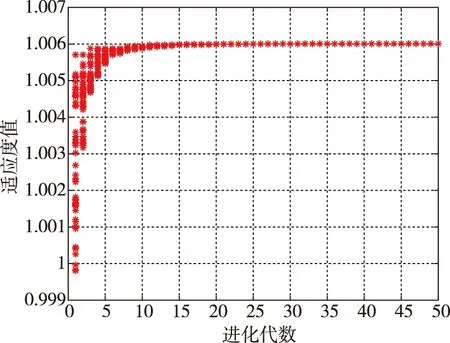
图3 进化50代后种群优化目标适应度值分布图Fig.3 Distribution of population objectives fitness value after fifty generations of evolution

由图2、图3可见，经过遗传算法进化计算，在15代以后适应度值收敛至最大值约1.006；经过约38代，上面级组合体初始停泊轨道远地点高度Ha0收敛于18 880 km附近；经过约25代，上面级第一次变轨目标轨道远地点高度Ha1基本收敛于22 063 km附近；经过约32代，上面级第二次变轨段轨道系下俯仰角二次曲线拟合点俯仰角ϖmid基本收敛于0.4°附近；上面级第二次变轨段轨道系下俯仰角二次曲线拟合点时间Tmid收敛性差，因整个变轨段ϖmid基本接近于0，Tmid的取值对结果影响较小。因此，经遗传算法优化后，运载能力提升约6‰。取进化50代后的最优解，上面级第二次变轨段轨道系下俯仰角和偏航角对比曲线如图4和图5所示。可以看出，优化后俯仰角变化为曲线形式并且数值更接近于0，推力方向与飞行轨道方向基本一致；优化前后偏航角差别较小，均约为-0.017°的小量。

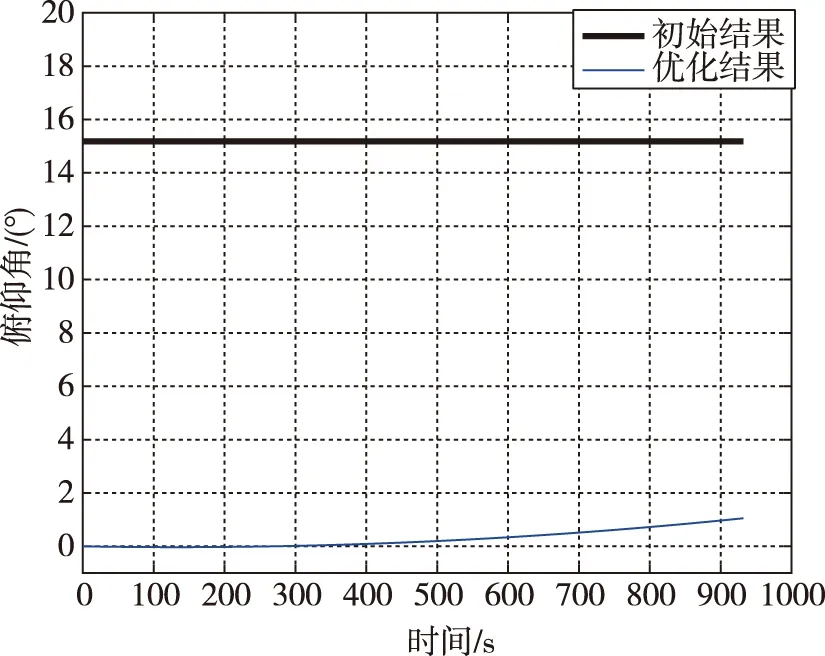
图4 优化前后上面级变轨段俯仰角变化曲线对比图Fig.4 Comparison of pitch angle curves of upper stage maneuver phase before and after optimization

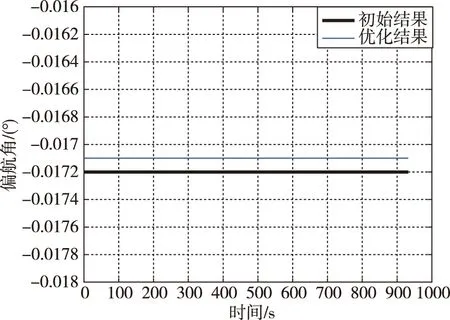
图5 优化前后轨道系下偏航角变化曲线对比图Fig.5 Comparison of yaw angle curves of upper stage maneuver phase before and after optimization

5 结论

针对采用火箭上面级直接入轨发射导航卫星MEO轨道任务研究需求，建立轨道动力学和变轨迭代计算模型，分析轨道优化的可能因素，采用自适应遗传算法对发射轨道进行优化，最后采用数值仿真对本文所采用的轨道设计和优化方法进行验证。结果显示，上面级直接入轨发射MEO轨道设计方法正确，能够准确将卫星送入目标轨道；轨道优化方法有效，能够小幅提升运载能力，实现优化设计的目的。本文为基于轨道与优化方法的理论分析，工程实际中还需要考虑基础级三子级承载变化引起的结构加强增重、载荷支架质量变化等因素对运载能力的影响。