汽车侧门开关疲劳瞬态仿真方法研究

奇瑞汽车股份有限公司 汽车工程技术研发总院，安徽 芜湖 241009

汽车侧门作为车身系统中的重要组成部分，其性能的好坏直接影响着整车使用性能的高低[1]，如噪声、振动与声振粗糙度（noise vibration harshness,NVH）、安全、耐久、关门品质[2−4]等。特别是针对于汽车的轻量化设计，侧门的减重贡献量突出，因此对侧门的性能提出了更高的挑战。通过对侧门结构性能的分析，如模态、刚度、抗凹、下垂、过开等[5−7]，能在产品设计前期很好地规避风险，缩短开发周期。但是对于汽车结构中使用频率较高的侧门而言，出现问题主要是以经常开关造成的疲劳损坏为主，而开关疲劳分析能很好地贴合实际工况。

目前，常用的开关模拟方法有惯性释放法和瞬态动力学分析法[8−13]。惯性释放法效率高，但无法精确地模拟侧门在关闭中的真实过程，如接触、密封条、锁冲击振荡等，因此计算结果精度不高[14]；瞬态动力学分析更接近实际，但是动态模拟复杂，需要考虑多种非线性边界条件的影响，因此，如何准确地模拟出侧门的运动状态是分析开关疲劳的关键。本文以某车型的前侧门为例，采用Abaqus/Explicit 进行瞬态响应分析，通过与实验加速度的对标，修正密封条阻尼参数，使测试和仿真加速度具有较好的相关性，获得准确仿真模型。采用Ncode 软件开展疲劳仿真分析，预测出风险位置，并优化改进，最终实验验证满足要求。

1 汽车侧门开关疲劳分析方法

侧门的开关疲劳分析主要分为2 步：1)进行侧门开关过程的瞬态分析，通过有限元建模、材料参数及加载工况的输入，在Abaqus 软件中求解得到焊点力与力矩、钣金应力应变的时间历程；2)将计算结果导入到Ncode Designlife 软件中，关联焊点 S-N 及钣金 E-N 曲线，通过 Miner线性累积原理，得到多次循环下的损伤。最终根据目标，判定是否满足要求，不满足需要优化改进。具体流程如图1 所示。

图1 汽车侧门开关疲劳分析流程

2 有限元模型

Abaqus/Explicit 采用中心差分法对时间进行积分，求解显式运动方程，因为不需要求解线性方程组，所以每个增量步的费用较低，特别适用于求解需要分成许多小的时间增量来达到高精度的动力学仿真，如冲击、碰撞等[15−17]。在Abaqus中，求解应力或位移的单元类型很多，本文中选用的是线性减缩积分单元提高分析效率。但是线性减缩积分单元由于存在“沙漏”问题，采用线性减缩积分单元模拟承受弯曲载荷的结构时，沿厚度方向上至少应划分4 个单元[18]。

截取1/4 车身模型，如图2 所示，约束截取位置处全部自由度。控制网格质量如翘曲度、长宽比、倾斜角度、雅克比等，特别是网格尺寸，过小的网格尺寸会导致计算稳定时间增量变小，使计算效率急剧下降。针对此问题，可以采用质量缩放的方法控制时间增量。然而使用时要注意，因为模型质量增加太大会使结果失真，通过能量守恒判断结果的合理性[19]。侧门开关疲劳的过程其实就是门在关闭瞬间从动能转换为内能的过程，关闭时的能量大概30%由密封条吸收，25%由缓冲块吸收，40%由锁吸收，其余5%由其他组件吸收[20]，因此密封条、缓冲块、锁的模拟尤为重要。

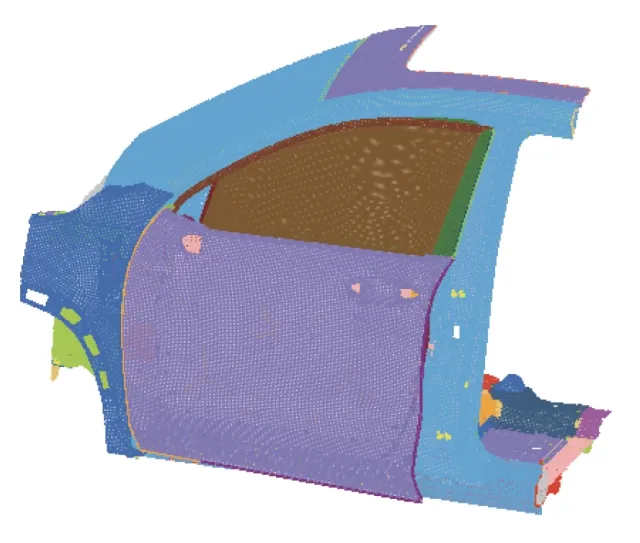
图2 分析模型截取示意

侧门的密封条主要由2 部分组成，门洞车身侧与侧门侧。密封条的内部结构非常复杂，如图3所示，在仿真过程中，要进行适当的简化。在建模中，密封条的形貌要保留，用于模拟变形和接触；抽取密封条外表面的中面用壳单元模拟，附上密封条的材料；密封条的刚度在侧门关闭过程中很重要，刚度过大使得关门困难，过小起不到吸能作用，而且不同位置的密封条刚度不一样，因此不同位置需要建立局部坐标系指定方向，刚度以一定数量的弹簧单元模拟，弹簧单元均布在密封条中。

图3 密封条实物截面结构及有限元模型

通常，密封条刚度由实验测得。密封条刚度实验样件与实际安装在侧门上的长度不同，需要通过公式将刚度转换到每个弹簧单元上：

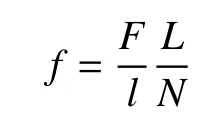
式中：f为单个弹簧单元在某压缩量下的载荷大小；F代表长度为l的密封条样件在某压缩量下的载荷大小；L为某段密封条的总长度；N为模拟某段密封条弹簧单元的总个数。本文密封条弹簧单元间隔为20 mm，由于实测的刚度非线性段太多，可以选取多个值进行拟合等效，门洞侧的某段密封条原始的及等效后的弹簧单元刚度曲线如图4所示。

图4 密封条弹簧刚度曲线

缓冲块的建模规则与密封条类似，如图5 所示，建立缓冲块外部表面网格模拟接触，利用弹簧单元模拟其刚度，刚度值由实验测得。

图5 缓冲块有限元模型

锁机构的结构比较复杂，在建模中只有准确地模拟锁的运动状态才能准确地模拟门关闭过程。如图6 所示，锁机构中背板、锁舌、锁钩、棘爪采用实体单元建模，其中棘爪及锁舌外圈单位需要根据实际材料附上材料属性，在接触上后能更好地吸收内能；销轴以及扭转弹簧分开模拟，销轴通过梁单元B31 模拟，截面直径为销轴直径；扭转弹簧用前述弹簧单元模拟，扭转弹簧的刚度同样由实验测得。侧门在关闭过程中，锁钩首先与锁舌碰撞并接触，迫使锁舌转动，从而使锁柱进入到锁舌和棘爪之间，达到半锁状态；锁舌撞击棘爪，使棘爪先向下转动，再向上卡住锁舌进入全锁状态。棘爪和锁舌之间通过自身的特征结构进行限位，使锁钩不能脱出。由于冲击力作用，全锁后锁钩会在锁舌和棘爪间来回进行振荡。

图6 锁机构有限元模型

侧门与车身通过铰链连接，铰链由3 部分组成，车身侧铰链本体及侧门侧铰链本体用实体建模，销轴采用Hinge 单元模拟。其他附件以质量点代替。

3 模型对标

在做实验的过程中，加速度是一个很容易测得的结果，可以通过加速度传感器获得该数据。因此，本文采用基于加速度对标的方法来修正模型。实验因传感器连接到电脑，如果在内部取点会影响侧门关闭；外部的取点主要根据铰链和锁对应外板位置，其余位置均布在门框边界及中部位置，实验测试加速度7 个位置如图7 所示。因铰链侧的加速度响应不明显，文中主要列取锁处及边界位置点P1、P4、P5的加速度响应图及对标结果。

图7 实验及仿真加速度位置

疲劳损伤的主要影响是幅值，因此把加速度的最小值a和最大值b作为主要目标进行对标。仿真结果与实验结果对标如图8 所示。

图8 加速度对标曲线

通过对比可以发现，锁在锁死后，实验加速度衰减迅速，但仿真结果一直在激荡，没有衰减。考虑到侧门在实际关闭的过程中存在各种阻尼，如空气、密封条、缓冲块等，因密封条面积较大，占主要因素。但是阻尼的获取比较困难，本文通过将阻尼等效在密封条上进行对标。设置密封条阻尼比为1%～5%，与实验加速度进行对标，列出P1点对标结果，如图9 所示。

图9 不同阻尼比的加速度对标曲线

通过结果对比，阻尼比在1%～5%变化时，加速度的第一个峰值变化不大；随着阻尼比的增大，加速度衰减越快，但是幅值并不是线性的下降，比如3%的加速度幅值比2%大。与实验加速度对比，当阻尼比为2%时，最大和最小幅值及衰减过程相关性较好，因此选取密封条阻尼比为2%进行疲劳计算。

4 疲劳验证

计算得到的损伤结果如图10 所示，最大损伤在靠近下部门框处焊点，损伤值为1.6、1.1。

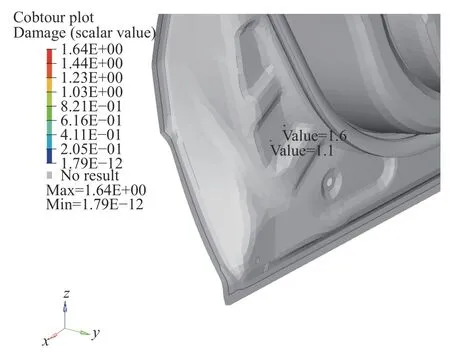
图10 疲劳仿真结果

实验开裂位置如图11 所示，与仿真最大损伤位置为同一处焊点，验证了仿真与实验的相关性较好。对开裂焊点进行优化改进，在开裂位置增加一段结构胶，仿真得到损伤为0.028、0.017，最终通过实验验证。

图11 开关疲劳实验结果

5 结论

1）本文建立了侧门开关疲劳的瞬态仿真方法，并与实验结果进行对标。

2）阻尼对于侧门加速度响应具有较大的影响，特别是幅值的衰减，当密封条阻尼比为2%时，仿真和实验具有较好的相关性。

3）后续还需要研究侧门在关闭过程中空气、缓冲块、锁的阻尼等，进一步提升仿真精度。