基于优化VMD与欧氏距离的柴油机故障识别*

张海龙, 宋业栋, 李 鑫, 毕凤荣, 毕晓博,汤代杰, 杨 晓, 马 腾

(1.潍柴内燃机可靠性国家重点实验室 潍坊，261061) (2.潍柴动力股份有限公司发动机研究院 潍坊，261061)

(3.天津大学内燃机燃烧学国家重点实验室 天津，300072)

引 言

内燃机是现阶段最为主要的动力源之一，其工作状态直接影响整个机械系统的安全性与可靠性[1]。因此有必要对准确高效的发动机故障诊断方法进行研究，其中振动检测法由于结构简单，成本低廉等优点[2]，成为当前研究的一个热点。发动机振动信号含有大量背景噪声，因此需要对直接采集到的机体振动信号进行处理才可准确提取故障特征[3]。在众多处理方法中，常用的有短时傅里叶变换[4]、小波变换[5]、经验模态分解(empirical mode decomposition,简称EMD)[6]等。但是这几种算法都存在一定程度上的不足，如相近频率无法分解、模态混叠、计算效率较低等[7]。因此笔者引入了变分模式分解算法[8]，其采用变分原理构建，规避了递归模型的固有缺陷，并已应用于轴承与其他旋转机械等的故障诊断，在工程应用中展示了巨大的潜力[9-10]。

为解决当前算法计算准确性与效率较低，以及常见的算法与故障只能一对一诊断[11]等问题，笔者将VMD作为主体算法与鲁棒性独立分量分析联合使用，分析发动机振动信号，并结合模糊C均值聚类与欧氏距离区分故障类型，从而实现利用同一种计算方法对多种故障进行准确高效诊断的目的。

1 算法原理及优化

1.1 VMD算法原理简介

VMD算法的作用是将一个信号f分解为若干个离散的模态分量uk。对于每个模态分量uk，其中心频率随分解层数而定，且每个模态几乎都是紧贴在中心频率ωk上的[8]。

首先，对于每个模态分量uk使用希尔伯特变换处理信号，得到单边谱

(1)

接下来将一个预估的中心频率e-jωkt混入uk的解析信号中，将模态分量uk的频谱转移到基频带上

(2)

通过式(1)(2)处理后，带宽即可通过解调信号的高斯平滑也就是L2范数的平方获得。得到的受约束的变分模型为

(3)

为求解这个问题，引入了二次罚项α和拉格朗日乘子λ，从而得到不受约束的方程。基于此可得增广拉格朗日公式

L({uk},{ωk},λ):=

(4)

最小值问题则转化为求解增广拉格朗日鞍点问题，可以容易地在频域中解出[8]

(5)

(6)

拉格朗日乘子λ可以表示为

(7)

然后，通过换向数乘法(alternate direction method of multipliers,简称ADMM)依次反复局部优化uk，ωk，λ完成求解。即在计算过程中将uk，ωk，λ初始化之后进行交替迭代，直至满足迭代停止条件

(8)

迭代完成后，VMD算法输出K个模态分量。

1.2 FCM原理简介

在故障的分类中，文中采用了FCM的基本计算原理[12]，简介如下。

已知数据样本X={x1,x2,…,xn}的模糊分类矩阵U=[uij]c×n和聚类中心C=[c1,c2,…,cn]T，其中：c为聚类中心个数；n为样本个数；uij为任意点数据xj相对聚类中心cj的隶属度。

数据点xj相对聚类中心cj的欧氏距离为

dij=‖xj-ci‖=(xj-ci)T(xj-ci)

(9)

FCM的目标函数为

(10)

FCM算法采用迭代法最小化目标函数。具体计算过程如下。

1) 确定聚类中心个数c，模糊加权数m，迭代停止条件ε与最大迭代次数kmax，初始化隶属度矩阵U。

2) 计算聚类中心

(11)

3) 由聚类中心更新隶属度矩阵U

(12)

4) 当‖Uk+1-Uk‖≤ε或迭代次数达到kmax时停止迭代，得到输出结果。

2 VMD算法的优化

2.1 算法优化思路

VMD算法也存在一处不足，即分解层数需要人为选择，若分解层数不合理，则会出现过/欠分解现象。通过上文对VMD的简介，可知其中最主要的为uk与ωk的迭代过程。在这两个参数之间，中心频率ωk更容易控制，且中心频率ωk的初始化对计算的准确性与效率有着很大的影响。所以，若能够将中心频率的初始值设定为发动机故障特征频率的近似值，即可在保证计算准确的前提下，提高效率。对于这一估计的初始值，虽然精度要求较低，但是必须兼顾各个工况下的振动信号特点。下面将以实际数据为例，介绍分解层数与初始值的预估方法。

同时要特别说明的是，在实际检测中只能通过先验分析获取故障特征频率的范围，而不是一个准确的值。若利用滤波、小波变换、EMD等方法容易造成特征分量丢失信息或包含噪声过多等问题。VMD方法则可以利用其自适应性的优势，准确地分析故障特征。

2.2 基于实验数据的算法优化

本次研究以某柴油机常见的喷油提前角异常、气门间隙过大和气门间隙过小3种故障进行研究。采样频率为25 600 Hz，在分析过程中分别选取了在2 100 r/min，100%负荷下的正常工况，喷油提前角故障，气门间隙偏大，气门间隙偏小各50组振动信号数据。其中：气门间隙偏大工况为第1缸排气门间隙增大0.1 mm，第3缸进气门间隙增大0.1 mm；气门间隙偏小工况为第1缸排气门间隙减小0.1 mm，第3缸进气门减小0.1 mm。为确定一个合适的分解层数与相应的中心频率初始值，分别对上述200组信号进行5，6，7，8层分解。计算各个分量的中心频率值，篇幅有限，以气门间隙偏小工况进行说明，结果如图1所示。

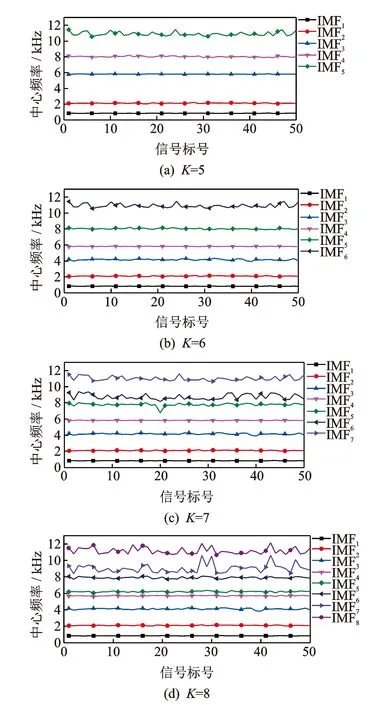
图1 气门间隙偏小工况信号分解结果Fig.1 The decomposition results of small valve clearance working condition

对于气门间隙偏小工况，K=6为整体最佳分解结果(对绝大部分信号为最佳分解)，因为当K=5时，存在相邻分量距离过大，即欠分解现象；当K>6时，各阶分量不仅波动剧烈，且部分相邻分量中心频率过于接近，即出现了过分解现象。基于同样的分析，可得对于喷油故障工况、气门间隙偏大、正常工况的最佳分解层数分别为7，6，6。基于这一分析，计算了上述信号最佳分解时各阶分量中心频率的均值，如表1所示。

表1 各阶分量中心频率均值Tab.1 The average values of center frequencies

基于表1，文中将K值设为6，对应的中心频率迭代初始值为对各个分量中心频率均值取平均，其中喷油故障的IMF7分量将与IMF6共同计算。结果为：0.82，2.11，3.93，5.75，7.70，10.49 kHz。基于这一结论重新对上述信号进行分解，其中心频率如图2～5所示。

图2 喷油故障Fig.2 The fuel injection failure

图3 气门间隙偏大Fig.3 The big valve clearance

图4 气门间隙偏小Fig.4 The small valve clearance

图5 正常工况Fig.5 The normal working condition

从图中可以看出，算法取得了理想的效果，不同工况下的分量中心频率间隔均匀，波动平缓，经计算平均迭代次数也减少了15%。尤其是喷油故障工况，即使分解层数改变也未出现过/欠分解现象，算法的简便性得到了很大的提高。

3 故障特征提取

VMD算法不能分解不同振动源的同频率信号，所以需利用ICA算法进行再次处理。ICA算法要求通道数不得小于信号源的数目，因此为达到单通道信号分解的目的，文中采用VMD算法对原始振动信号的分解结果作为ICA算法的输入。特别要说明的是，经过对比文中采用Robust ICA对信号进行处理，对比过程限于篇幅不再展示。

在故障指标选取过程中，将原始信号VMD算法分解结果重构信号的4阶累积量作为第1个故障指标(fault index 1，记为FI1)，接下来将Robust ICA算法进一步分解结果重构信号的四阶累积量作为第2个故障指标(fault index 2，记为FI2)。因为高斯随机信号的四阶累积量恒为零，且四阶累积量对于非线性信号的识别能力较好，因此选择这一参数能够较为准确地提取由发动机故障引发的振动特征。在原始FCM中一般直接设置分类数为4进行处理，如图6所示(g=9.8 m·s-2)。

图6 模糊聚类结果Fig.6 The results of original FCM

具体识别结果为：将7个气门间隙偏小故障识别为喷油故障、气门间隙偏大未能识别15个工况点、气门间隙偏小未能识别其中7个故障点并将15个气门间隙偏大点识别为气门间隙偏小，只有正常工况全部识别正确，其整体正确率为89%。在样本量不大的情况下出现了较高的错误率，证明这种方法不能直接用于发动机故障诊断。

观测上述数据发现，正常工况的识别率较高，因此笔者进行如下优化：逐个将其中每一种故障与正常工况两组数据利用FCM进行2分类，从而获得各个故障工况的聚类中心，而正常工况的聚类中心则取多次计算的平均值(FCM要求分类数不得小于2)。接下来计算每个工况点与其中一种工况聚类中心的欧氏距离，最终通过距离来确定故障类型。具体的诊断流程如图7所示。

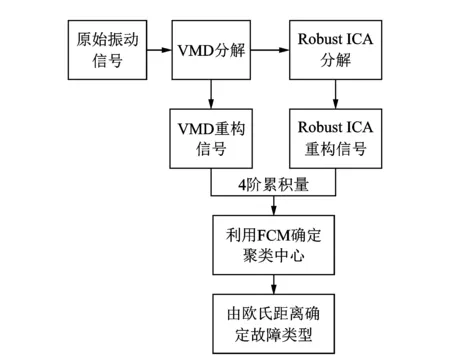
图7 诊断流程图Fig.7 The flow chart of diagnosis

利用上述方法，需要确定可获得最佳分类效果的聚类中心。具体计算获得的聚类中心如表2所示。

表2 聚类中心点Tab.2 The cluster centers

根据以上结果，计算各个工况点相对每个聚类中心的欧氏距离。通过对比，其中喷油故障聚类中心作为参考点，可以得到最佳的分类效果，如图8所示。

图8 距油故障聚类中心的欧氏距离Fig.8 The euclidean distance to the cluster center of fuel injection failure

根据这一结论，可以确定以下故障分类阈值，距喷油故障聚类中心的欧氏距离≤1.0×107时，为喷油故障工况；1.0×107～2.9×107时，为气门间隙过小工况；2.9×107～7.5×107时，为气门间隙过大工况；大于8.5×107时，为正常工况。

通过这一区分方式，上述故障区分正确率可达98.5%，其中仅有1个喷油故障点与2个气门间隙偏小故障点判断错误，相较原始区分方式有了很大程度的提高。

4 结束语

笔者采用振动信号对发动机故障进行诊断，以利用单一通道信号快速准确地识别多种故障为目标进行了研究，得到以下结论：通过优化VMD中心频率迭代初始值，在保证准确性的前提下，提高了算法的简便性与计算效率。并针对发动机中可能存在的不同振动源的同频率信号，选择Robust ICA算法对VMD分解结果再次处理。同时选择将两个阶段分解结果重构信号的四阶累积量作为故障指标，在原始FCM算法确定聚类中心的基础上，利用工况点与喷油故障工况聚类中心之间的欧氏距离区分故障类型，取得了较高的正确率。

但是此次的研究选取故障类型较少，算法计算效率也仍存在提高空间，这将是今后工作方向。