提升思维互动含量的在线教学策略
——以“锐角的三角比”单元复习为例
◎ 孙琪斌
一、问题的提出
2020 年3 月2 日,上海市中小学开启在线教学,确立了“一个平台、多种终端、多个渠道”“统一课表、自主选择、双师教学”“视频授课、先录后播、适时互动”等基本原则。广大一线教师加入了大规模在线教学的行列之中。
总体而言,在线教学能够延展学生的学习空间,为同步教学、异步达标搭建新的平台。学习者在家里就可以便捷、轻松地学习到全区甚至全市的课程,遇到困难时,还可以反复观看教学视频之中的某个片段。
然而在在线教学的过程中,笔者遇到了一些困惑,比如平时习惯了巡视课堂蓦然发现熟悉的学生全部都消失在视线之外;讲到关键内容的时候,想用“敲黑板”的方式聚焦学生的注意力,忽然发现目前认认真真听课的人数都成了一个未知数。围绕这些困惑,笔者梳理总结为以下三个问题。
(一)学生未必时时在线,面对面的实时互动较难实施
线下教学时,教师可以一览无余地观察到每个学生的学习状态。尤其对于部分学习比较困难的学生,教师可以及时组织针对性较强的第二次教学甚至第三次教学。
在线教学时,教师虽然也可以实时便捷地向学生提问,但是被提问的学生,有可能只是虚拟在线,也有可能其学习注意力并没有聚焦在问题上,因而面对面的实时互动较难实施。
(二)缺失了学生思维的即时参与,在线教学更容易偏离学习需要
线下教学时,教师即使不使用课堂提问的方式,也能够便捷地把握学生的思维状态,比如只需走到学生身边浏览作业即可知道学生学习过程中的真实需要。
在线教学时,教师则难以即时捕捉到这些基于学生的无声思维与无形画面。缺失了学生的思维即时参与的在线教学更容易偏离真实的学习需要。
(三)越来越大的生生差异,加剧了同步教学与个性学习之间的矛盾
线下教学时,教师可以在同一个物理空间内多渠道、多层次地组织生生互助,因此基于新知学习的生生差异能最大限度地得到控制。
在线教学时,由于分布在不同的物理空间,从某种意义上而言,学生的实际学习状态是一个难以控制的变量。因此,在线教学可能使得生生差异越来越大,从而进一步加剧同步教学与个性学习之间的矛盾。
以九年级数学总复习为例,线下教学时,教师可以同时检测多个学生基础知识、基本技能的达成情况,进而即时便捷地开展第二次教学;也可以组织各个小组的组长同时检查各自小组成员的达标情况。
然而在线教学时,教师实施类似的操作则相对困难一些。如何更好地拓展在线教学的师生互动,促进师生之间的思维交流?下面以笔者在空中课堂执教的一个教学片段为例,分享教学经验。
二、促进教学互动、提升思维交流含量的教学策略
(一)关注数学的联系与发展,重视数学习题的源与流
促进教学互动,教师一方面关注的是学生学习数学的兴趣,另一方面关注的是基于数学知识以及数学思想方法的思维流动。以数学知识之间的联系与发展、数学思想方法的选择与优化促进学生思维的流动。
例如,在“锐角的三角比”单元的复习过程中,为了更好地激发学生的学习兴趣,教师要引导学生感悟建立锐角的三角比的意义,从一个内角为30°或45°的直角三角板与锐角三角比的概念之间的联系与发展的视角切入,突出数学的联系与发展,从特殊到一般,引出锐角的三角比,如图1 所示。

图1
为了更好地激发学生的学习兴趣,教师采用的另一个措施就是:揭示数学习题的源与流,让学生知道题目是如何生成的。于是教师设计了以下例题。
例1如图2 所示,在△ABC中,∠C=90°,∠A=30°,BC=1。点D在边AC上,且∠DBC=45°。求sin∠ABD的值。
看见数学习题的源与流,重点在于题目的变化过程:变化过程中有哪些知识或方法始终保持不变?如何以不变应万变?为此,教师又利用两块三角板拼出了如图3 所示的图形,以此引导学生发现问题、提出问题、分析问题和解决问题;引导学生从变中找不变,体会不变应万变的通性通法。
在与本区九年级数学教师一起教研的过程中,笔者曾经尝试将数学教师视为学习者,让教师成为教研活动的主持人或主讲人,意外发现:一旦将学习者视为学习的主体,将学习者推上舞台,原有的担心都不复存在,活动中反而能够经常出现一些意想不到的精彩。由此,笔者领悟到在线教学要让更多学生的思维过程或学习结果即时可见,要给学生搭建展示的舞台,让学生能够说话,让学生有话可说,这是促进教学互动的关键。

图2

图3
例如,教师可以这样引导学生观察:从求sin∠ABD的视角,尝试说出一个常用策略或一条解题经验,也可以组织学生叙述自己当前遇到的困难:我知道自己做错了,可是我究竟错在哪里?又如,教师还可以引导学生叙述其思考的变化过程:最初是如何思考的?听了大家的发言之后,目前又是如何思考的?再如,教师也可以组织学生针对共享在屏幕上的作业进行点评,在此基础上再分享其他的方法,从中评选最受欢迎的方法。
对于学生而言,在期待自己的作业能够被老师分享给全班同学的过程中,在期待自己的学习困难能够得到有效指导的时候,在发现自己的解题方法能够得到老师(或所崇拜的同学)认可的时刻,这些源于学生内心深处的学习期待其实已经悄悄地转化为一种难得的教学资源。让更多的学生都能够感受到自己的课堂存在,让更多的学生对即将开始的在线教学有所期待,这是吸引学生能够坚持时时在线的有效策略之一。
(二)从一维到多维,让更多的解题方法同时呈现在屏幕上
对于在线教学而言,部分学习者跟不上教学者的讲授速度,因某个环节听不懂而导致学习兴趣下降或产生学习焦虑,是一个大概率事件。基于这种情况,笔者认为在线教学需要从“具体解题方法的线性呈现(一维)”向“多角度思考方向的归纳与点评(多维)”转变。
所谓多维呈现,就是将教师的教学经验与学生已经想到的辅助线以及可能想到的辅助线,融合于一题一图,示例如下。
例2如图4 所示,在△ABC中,∠C=90°,∠A=30°,BC=1。点D在边AC上,且∠DBC=45°。求sin∠ABD的值。
想一想:从“构造以锐角∠ABD为内角的直角三角形”的角度展开思考,下面所示的四种方法中,你首先想到的是哪一种?
教师在讲解例题的过程中,可以平行呈现本班学生在学习过程中已经得出的多种解题方法或思考方向,也可以呈现其他班级学生的学习成果。
从以知识讲授为中心的教学走进以思维分享为中心的教学,引领学生从多个视角展开思考方法背后的算理。从“讲授解题方法为核心”转变到以“体验通性通法为核心”,具体教学流程如图5 所示。

图4

图5
(三)重视小组学习,从知识讲授向基于异步达标的跟踪监测转变
学生之间的差异是客观存在的,即使是由同一个学习层次的学生组成的分层教学班,学生与学生之间还是会存在差异的。因此,从班级集中授课向基于小组的分类指导转变,就显得特别重要。
例如,在学习过程中遇到了困难A,经过线上授课之后,困难A 仍然在部分学生身上存在,那么我们就可以引导学生以此组建一个学习群(简称A 群)。
教师可以这样告诉A 群的成员:什么时候解决了困难,什么时候再离开A 群。当然教师也可以指派已经学会的学生进入A 群开展具体指导。类似地,引导在学习过程中出现了困难B 的学生,自发组建学习群B……针对同一个学习内容和同一个教学班,没有遇到学习困难的学生可以在完成当前内容之后,分别进入困难A、困难B、困难C 等小组的学习群,以学促学。
从基于基础知识与基本技能的视角,教师可以这样落实异步达标:①对于学习比较困难的学生,教给他们容易复制模仿的学习方法,比如记忆特殊角的锐角的三角比。②对于中等成绩的学生,教师可以让他们一起共享多种记忆锐角三角比的值的方法,并组织他们讨论:在Rt △ABC中,∠C=90°,sinA与cosA之间有什么关系?tanA与cotA之间有什么关系?③对于学有余力的学生,教师可以组织他们研究教材中特殊角的锐角的三角比表格所蕴含的规律。
从基于学习经验与数学思维的视角,教师可以这样落实异步达标:①对于学习比较困难的学生,要求他们学会一种解题方法,比如会用如图6(a)所示的方法求sin∠ABD的值。②对于中等成绩的学生,教师可以要求他们学会能够在如图6 所示的四个解题方向中,选择适合解决本题的方法,并尝试用多种方法求sin∠ABD的值。③对于学有余力的学生,教师则可以要求他们反思如图6 所示的四种解题方向的利与弊,然后在此基础上思考“还有其他方法吗?你最喜欢哪个方法?尝试求cos∠ABD的值、tan∠ABD的值和cot∠ABD的值”。
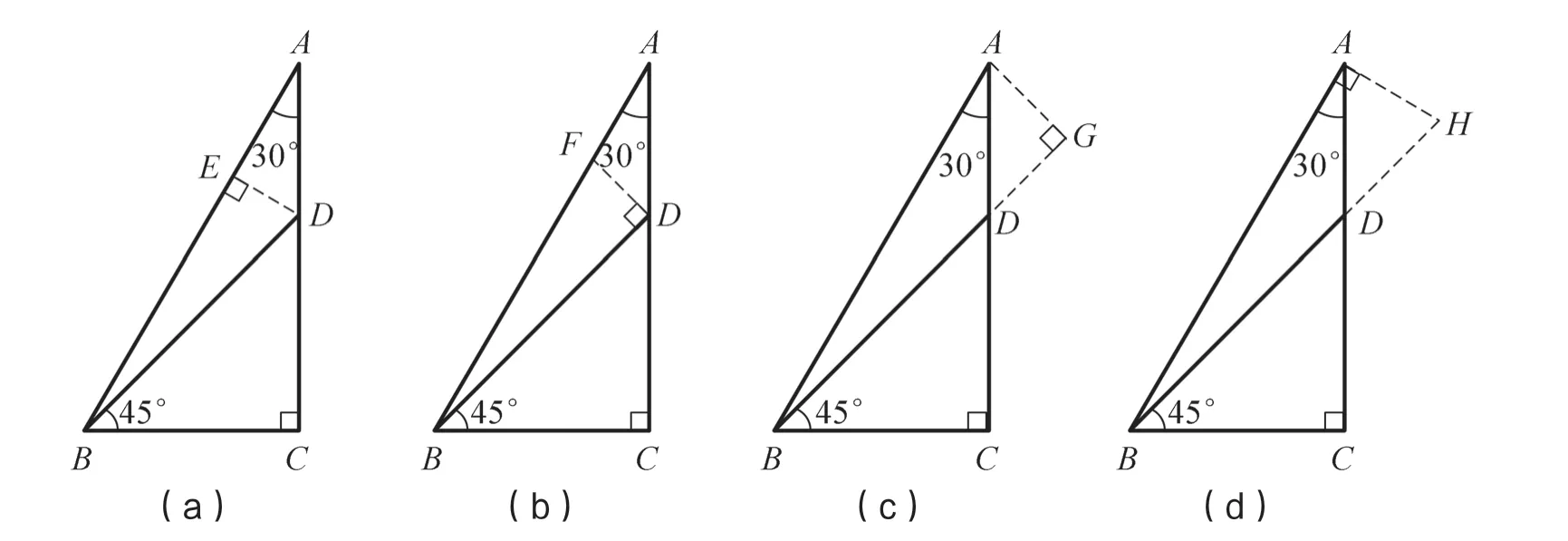
图6
三、结语
在线教学更容易拓展教学规模,从线下教学的几十人拓展到几百人,这是在线教学的优势。然而,在线教学中面对面的实时互动难以实施、学生的思维参与难以即时融入、生生差异可能会日益增大等问题也是无法回避的客观存在。
上文提到的激发学生时时在线的部分教学策略,比如从“教师讲”到“学生说”、分享学生作业、从班级授课到小组学习、异步达标等,只是笔者的教学感悟。在更大范围内进行复制推广的关键,还在于教学者在潜意识要有这种教学理念,并能够从学生视角去思考问题。在学中教、因势利导,且行且反思;分层教学、异步达标,任重而道远。

