基于数据驱动的非线性内波对水下潜体运动影响仿真分析

高国兴，江禅志，赵建昕，武志东，张西托，王立伟

(海军潜艇学院,山东 青岛 266199)

海洋内波是在濒海海域广泛存在的海洋现象,能够引起海水次表层出现较强的波动。据文献报道,在南海海域已有超过百米量级内孤立波(以下提及的内波或非线性内波均指此类)垂向振幅,以及流速达到 3 m/s 的海洋内波实测记录[1]。由于这种内波引起的海洋水体波动现象多出现于海洋次表层,具有隐蔽性,诱导的流场剪切和海水密度变化较强,具有突变性,并且，其发生区域也有一定的随机性,因而，其存在对于水下特定深度活动的潜体(潜艇或水下潜航器)具有较大威胁[2-6]。事实上,由于海洋内波造成潜艇水下航行安全的重大事故已不是个例,例如，美国“长尾鲨号”潜艇在大西洋海域沉没以及以色列“达克尔号”潜艇在地中海的失事等，或都与较强振幅海洋内波的影响有关[3]。

这种具有较强振幅的海洋内波一般称为非线性内波或内孤立波(波列),相较于线性内潮波而言,其具有局部流场的突发性以及振幅较大等特点[4]。为了分析非线性海洋内波对水下潜体航行的影响,有必要通过内波数值模拟计算和六自由度(DOF6)运动模型仿真定量分析海洋内波对水下航行潜体的影响,给出潜体海洋内波区安全航行的防护措施或科学处置方法。

为了定量分析该类型内波对水下潜体运动的影响,首先，基于内波动力学控制方程(IWE)的数值计算方法,给出了非线性海洋内波流场和密度场空间变化,并以此作为影响水下潜体航行姿态变化的外部驱动数据源。在不考虑潜体运动对水体反向影响和耦合的条件下,给出了仿真流程，并利用六自由度潜体运动方程仿真[7]，分析了不同潜深和初速度下六自由度潜体通过以背景驱动数据表示的海洋内波区时的运动响应,并由定量化的运动响应结果及内波特征给出了潜体水下操纵的合理化建议。

1 海洋内波空间变化驱动数据模拟

为了定量分析潜体水下运动过程中受海洋内波影响而产生的姿态变化,首先，需要建立用于内波数据计算的内波动力学模型。本文基于原始变量形式的海洋内波动力学控制方程(IWE)和非线性海洋内波“L”下陷生成方法,通过设定初始场和特定边界条件得到了由“L”下陷和海底地形作用产生的具有较高分辨率的海洋内波流场和密度场变化的动态数据[8-9]。

用于描述海洋内波的原始变量形式海洋内波动力学控制方程(IWE)为:

(1)

ρt+·(ρU)=0

(2)

·U=0

(3)

其中，U=(uw,vw,ww)T表示内波区流场,uw、vw、ww分别为内波引起的水体的三个速度分量(单位为m/s);ρ为水体的密度,p表示压力,FU表示外力,μ为水体的动力学黏性系数。本文采用该模型的数值化解决方案,并通过设定初始场和特定边界条件,可以得到海洋内波的动力学数值模拟结果。图1给出了采用该模型得到的一组典型结果,图中的色标为水体的扰动密度(单位为kg/m3)。水体设计为有跃层存在的情形,并在左侧边界有一周期性潮流边界条件,上下两图对应的是不同时刻内波场,可以看出内波的生成及传播过程对跃层的扰动情况。

图1 内波场数值仿真结果(深度100 m，跃层深度20 m)

通过分析内波动力学数值计算结果,可以得出非线性海洋内波的几个主要特点。

1)非线性海洋内波被激发生成后,以孤立波或波列的形式向前传播,内波的速度和强度与跃层强度、潮流强度以及海底地形变化有关。

2)前导波所在位置水平和垂向速度剪切变化明显,即内波能够引起局地流场的突变,并且，不同深度或位置速度剪切差异较大。

3)海洋内波能够引起局地密度场的显著变化,其中，前导波所在位置跃层深度处,密度场沿垂向和水平方向变化最为显著。

2 基于数据驱动的潜体水下运动仿真

一般而言,海洋内波对水下运动体影响表现在多个方面,其中，对潜体速度和净浮力的扰动是重要因素之一。就流场而言,根据潜体运动稳定性的一般研究方法[10-11],当潜体以一定的速度进入内波区时,假设内波导致的流场仅对潜体当前运动参数中三个速度分量有影响,并且，这种影响只是施加于某一瞬时时刻。即在潜体当前位置,“检测”到(指内波流场的分布已知且发生变化的情况)内波流场分量相对于潜体前一时刻所在位置处发生了变化,致使潜体运动参数在瞬时发生改变。基于这一考虑,潜体的速度变化可以表示为一阶扰动量和上一时刻速度之和,记为

u=u0+Δu

(4)

其中,u0为潜体受扰动之前的速度矢量,Δu为内波流场矢量的突变,u为潜体受扰动之后的三分量速度矢量,即u=(u,v,w)T。受扰动之后的速度矢量的时间响应满足刚体运动动量和动量矩定理给出的六自由度运动方程:

(5)

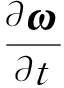
(6)

其中,m表示潜体的质量,t为时间,ω=(p,q,r)T是角速度矢量,J为刚体运动惯量,F和M分别表示潜体受到的惯性力和力矩,其具体表达形式可以参考文献[5，11]。此外,为了求解该方程组还需要增加表示位移变量的方程。这样整个仿真计算需要求解一个具有12个维度的方程组,求解方法可以参考文献[7]。

由此不难看出,直接将受扰动的流场参数引入六自由度仿真模型中,计算可得到潜体在内波流场影响下的六自由度以及姿态、位移和角度等变量随流场扰动而产生的响应情况。对于内波密度场变化对潜体影响的分析则相对简单。在六自由度运动模型中可以只考虑潜体净浮力变化项,进而计算潜体六个自由度及姿态受扰变化的响应情况。这一处理方法可以称为基于数据驱动的潜体受内波场影响仿真方法。

基于以上处理方法的分析,这里给出了潜体受内波场影响的仿真分析流程,图2是内波引起的流场和密度场对潜体运动影响的仿真流程,图3给出了图2中内波检测模块的子流程图。

图2 潜体受内波场影响仿真流程图

在流程图中,潜体运动过程的内波检测驱动模块的主要步骤如图3所示。

图3 潜体运动过程内波检测驱动模块流程图

3 仿真结果及潜体水下航行建议

3.1 仿真结果

本文根据给出的内波模拟及潜体受内波影响的仿真流程,首先模拟计算了一组由深度为500 m(含有水下地形海脊),跃层深度约为100 m的潮流激发生成的内孤立波,并选择了特定时间的流场和扰动密度场空间分布数据。然后，以此数据为外部驱动数据源,驱动六自由度潜体水下运动模型(模型参数参考了某潜体的数据),进而得到了潜体受内波扰动的运动响应。图4给出了内波密度和流场数值模拟结果。从图中可以分析得出,跃层深度约为100 m,厚度约为20 m,产生的内波振幅约为90 m(以水平6 000 m位置处的内波为参考)。图5是由该内波数据驱动不同初始条件的六自由度模型,以不同航速通过该内波区时仿真得到的内波场对潜体航深影响的变化曲线。为了便于分析,这里将潜体起始位置置于深度为100 m、水平相对位置在4 500 m处(如图4中小矩形框所示)。图6中的变化曲线仅考虑了内波流场变化对潜体航深的影响。由以上模拟和仿真结果可以初步分析内波场对水下潜体航行深度的影响。

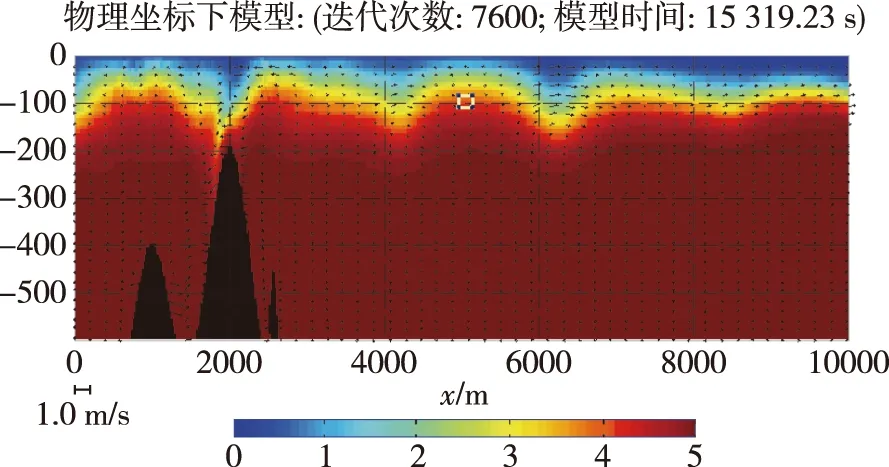
图4 内波模拟结果(深度500 m，跃层深度约为100 m)

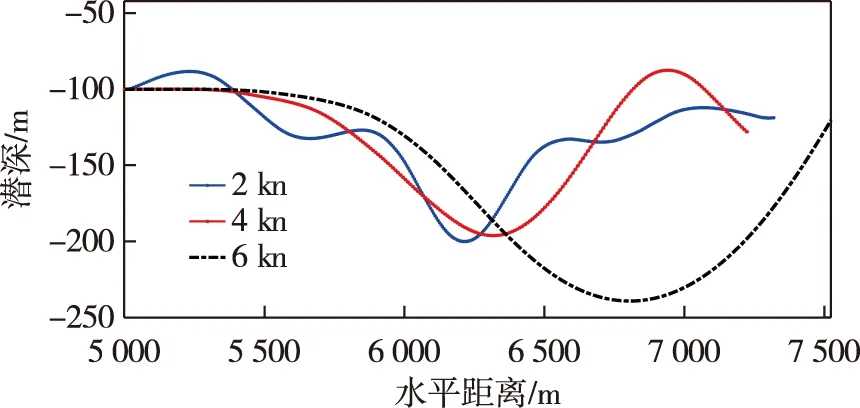
图5 潜体以不同航速通过内波区时潜深变化(考虑流场和密度场影响)

图6 潜体以不同航速通过内波区时潜深变化(仅流场影响)

通过分析以上仿真结果，可以得出如下结论:

1)海洋内波对潜体水下航行运动有重要影响,特别是对潜体航深变化，影响显著。

2)海洋内波对潜体水下航行影响主要来自内波引起的密度场和流场,其中，密度场影响较大，而流场的影响相对较小。

3)潜体以不同航速航行时，受内波的影响不同。当以较低的航速经内波区时,受内波的影响更大,潜体会随内波波动,当航速较高时这一波动明显减弱,但是，由于惯性而产生较大航深。

此外,在研究中可以通过设置不同的内波场、不同的潜体初始条件分析潜体受内波场的影响。事实上,内波对水下潜体的影响还表现在多个方面,如不同的内波振幅和不同的内波频率均对潜体水下航行有不同影响,对于潜体在同一内波区以不同潜深航行时,受内波的影响也明显不同,这里不再展开分析。

3.2 潜体内波区水下航行的建议

本文通过数值模拟或预报内波的生成、传播过程，并采用以上方法分析潜体通过内波区时的姿态变化、深度变化、姿态响应,同时，结合适合潜体水下航行的深度、姿态(纵倾、横倾、升速率等)以及净浮力等条件,可得出潜体如何避开内波影响及相应的处置建议。

1)内波对潜体水下航行的影响表现在内波造成跃层界面的起伏,其本质是密度场和流场的空间变化造成的,并且，密度场变化产生的影响更大。

2)潜体在内波区航行时，应熟悉该区域跃层深度和厚度等水文条件,熟悉内波传播的方向以及可能与内波相遇的态势。一般而言，跃层深度大、厚度小(但梯度大)时，易形成更强的内波;潜体航向与内波传播方向垂直时,由于在内波中的时间长短取决于内波波长和速度,因而可能造成的影响更大。

3)由于内波造成跃层界面的起伏一般在该界面深度处最强,因而，应减少在跃层强度最大深度的巡航时间,避免与内波的直接相遇。在无法避开内波的情况下,应着重考虑以下三种情况:一是当潜深在跃层深度以上时,如果水面无危险,可采用近水面或通气管航行;二是当潜深已在跃层之下时,应考虑内波通常呈现出的“倒钟”形特点,提高航速保持舵效,以较快速度通过内孤立波区;三是当潜深恰在跃层深度时,应注意潜体随波动的变化,也应考虑内波的“倒钟”形特点。如果波动频率高,说明航速低,应适当提高航速,如果无波动但潜深下降过快(超过允许值),应通过操纵升降舵调整,不宜直接排水调整。

4)在潜体通过内波生成源区(一般在海底地形突变附近)时,应考虑不同深度水层的流速和流向变化,在不能采用水面航行时，应选择较浅深度,在近水面或通气管状态航行。

4 结束语

根据以潜体受内波影响的仿真分析过程及流程,本文利用内波动力学模型计算了内波场数据,并以此作为外部驱动数据源,设定了潜体在内波区航行初始条件,采用六自由度运动方程，仿真得到了不同潜深和不同初始速度时的内波对水下运动潜体运动影响的定量仿真结果,并由此提出了潜体在内波区航行时的初步建议,对于潜体水下航行安全具有重要参考价值。但是需要说明的是,这里采用的是一种水体与水下潜体运动去耦合的处理方法,并未考虑潜体运动对水体的影响,因而该结果及结论适合于尺度较大的内波场对潜体的影响,对于耦合形式的处理方法和结果,将在后续研究中给出。