基于小学数学“学习任务设计与反馈层次”教学策略初探

司徒丽波

摘要：设计好的学习任务，可引发学生主动探索解决问题，为学生展开交流与对话提供丰富的生成性材料，也为提升学生思维水平、达成教学目标提供可能。基于教材的逻辑起点、学生的认知起点来设计学习任务;基于概念本质，强化概念多元表征;基于学生理解水平的提升，精心组织反馈，可以化解分数教学的许多疑难问题，帮助学生形成对分数概念的深度构建。

关键词：小学数学;学习任务;教学策略

有层次的教学反馈可以有效地帮助学生强化正确、改正错误，也能使教师在教学过程中及时掌握教学效果，调整教学计划、改进教学方法。概念教学历来是小学数学教学的重点和难点。分数概念从一个物体到多个物体的理解，是学生认识上的一个跨越。分数的意义内涵丰富，给学生的学习带来一定的困难。如何设计学习任务与合理组织反馈来开展教学，值得尝试。

一、基于学习起点，设计学习任务

数学学习过程是一个数学认知过程，新的学习内容与学生原有的认知结构相互作用，形成新数学认知结构的过程。在实际教学中，要充分把握认知起点，突破对单位“l”的理解。在三年级时学生已经初步认识了分数，两年后他们对分数有怎样的认识？笔者对本校五（3）班43名学生进行前测。

经过前测分析，我们发现多数学生对一个物体平均分表示分数这一旧知识掌握得比较好，而且已经具备把一些物体看作一个整体的意识。因此，设计学习任务时可以将学习的空间让给学生，教师直接提供学习素材，让学生自主表征分数的意义。

第一次试教：

学习任务：教师出示一个苹果图，一个圆形，4个圆形，你能表示出四分之一吗？

学生尝试表征，反馈时教师一一指着每幅图让学生解释。学生表述时提醒要怎样分、哪里是1份等问题，并不断纠正。最后把4个圆看成一个整体，抽象出单位“1”。

课后反思：大部分学生认可一个物体平均分，其中的1份就是四分之一，但是学生是凭直觉和生活经验去理解的，并没有和规范的分数意义理解挂钩。怎样均分、涂色？如何用语言完整表达？学生对4个圆看作一个整体，只用一个个例，还不能完全理解整体到底是什么意思。这时抽象的单位“1”太牵强。

那么如何改进呢？学生对分数的理解虽有认识，但对于分数的产生过程已经有点遗忘，教师应该通过“圈、均分、涂色、表达”这样一系列的活动让学生经历分数产生的过程，以利于学生去构建他们心中的“过程分数”。让学生在多种不同的素材中，先理解整体，从而进一步理解四分之一的含义。

改进教学设计：

学习任务一：一个饼、一条线段、4个圆、8个饼图、12个三角形，请你任选一幅图，表示出你心目中的四分之一。

反馈层次1：-个物体的四分之一，重点：帮助学生理清分数产生先要平均分，再涂一涂，表示出其中的一份。唤起学生对分数的初步认识，逐渐训练语言表征分数的意义。

反馈层次2：多个物体组成的整体的四分之一，重点：理解多个物体组成整体，在后三幅图的直观中，从初步理性的角度理解四分之一的含义。

学习任务二：我们用椭圆表示了一个整体，大家想想：椭圆里除了可以放1个物体、4个物体、8个物体、12个物体外，还可以表示哪些数量的物体？这个整体还可以表示更少或更小的数量吗？用这些整体还能表示出四分之一吗？

经过第二次试教，教师设计了两个学习任务，经过有层次的反馈，试图从两个维度让学生明理：一是求同，让学生在不同的物体中发现共同的特征，抽象出四分之一的含义;二是求异，对一个整体的认识进行拓展，通过几个问题的追问，学生既关注了单位“1”的不断变大，又兼顾了单位“1”的不断变小，进一步理解单位“1”的含义。

基于学生的学习起点，教师精心设计学习任务，让学生通过对多种素材的观察、想象，逐渐理解四分之一的含义和单位“1”的含义，由具体到抽象，让概念的产生变得自然。

二、基于概念本质，强化多元表征

数学概念特别是数学核心概念，需要能够运用多种形式进行表征，从多维度进行比较，才能够引发概念的多元联系，从而有助于学生形成较好的数学概念网络和知识体系。分数概念的形成，需要符号表征、面积表征、集合表征、数轴表征、语言表征等各种形式，只有让学生经历多元表征，才能全面深刻地理解分数的意义。

在第一次试教过程中，学生对分数用面积、集合表征掌握得较好，这源于学生对“部分整体”概念理解较好。因为学生对分数意义的理解，最初的理解就是“部分与整体”的关系，这也是分数意义教学的起点。教学中，通过提供不同的素材，在想一想、分一分、涂一涂等实践活动中，表征分数的“部分与整体”的含义，将分数的符号表征、语言表征、图形表征三者不断联结、沟通，使学生逐渐加深对分数的意义的理解。

课后反思：本单元后续教学真、假分数，以及分数的大小比较中，都借助了數轴来理解。那么，分数的多种表征形式中，用数轴表征在本课中也需要涉及。分数的含义着力点是部分与整体的关系，即分数表示分率的含义，但忽略了分数的另一重含义，即分数表示具体的数量含义。

改进设计：在第二次试教时，教师设计在数轴上表征分数这一学习任务，反馈时呈现学生中不同的思维方式，比如学生容易将数轴上标出的所有刻度看作整体，然后将其平均分成相应的部分，依据“部分与整体”的关系来寻找对应点。那么，教师就组织学生有层次地讨论、交流，明确数轴上的单位“1”是0到1这一段，理解分数的“测量”概念与“部分整体”概念。为了突破分数表示分率与数量的双重含义，设计了学习任务：（1） 一包糖重四分之一千克，怎样才能得到四分之一千克？（2）一包糖的四分之一，怎样表示？思考：这里的四分之一千克与四分之一有什么不同？反馈时呈现多种表征方式，让学生通过图形表征、算式表征、语言表征等，理解四分之一表示部分与整体的关系与表示具体数量的双重含义。

为了上好一节课的内容，教师应着眼整个单元的知识内容，甚至整个小学内容结构的体系，从整体的眼光来设计教学，让学生对知识的理解更加到位，为后续的学习打下坚实的基础。

三、基于学生理解水平的提升，精心组织反馈

《数学课程标准》指出：“小学数学课堂教学要关注师生之间的有效互动，要根据教学反馈信息来合理调控或调整教学进程。”所以，一个完整的教学过程必须包括学习者吸收信息并输出信息的过程。因此课堂上要精心组织反馈，反馈要有目标性，层次性。

分数的意义教学中，最核心的概念应该是分数单位，因为它是今后学习真分数、假分数及分数四则运算的基础。教材对分数单位只用一句话介绍：把单位“1”平均分成若干份，像这样的1份就是分数单位。

第一次试教时，笔者根据教材设计了这样几个问题：整数的计数单位有哪些？小数的计数单位呢？那么分数也有计数单位就叫做分数单位，比如四分之三的分数单位是什么？四分之三里面有几个四分之一？让学生先看书自学，接着以指名口答的方式进行反馈，从而完成分数单位的教学。

课后反思：分数单位与整数、小数的计数单位有联系吗？有什么相同之处？它们之间可以进行融合贯通吗？如果找到共性，學生就可以真正理解分数单位的含义，并且可以在头脑中形成对计数单位的整体结构体系。于是，大胆创新开始了新的尝试。

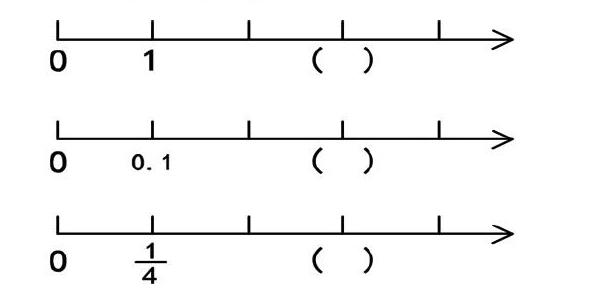
改进设计：第二次试教时，笔者设计了学习任务，提供了线段模型，让学生看图、填空。（如下图）

增加这一学习任务的设计，组织有层次地反馈，从整数的计数单位，到小数的计数单位，再到分数的分数单位，学生顺理成章地看到了它们之间的联系，从直观的线段模型中，比较容易地发现整数、小数是按照计数单位依次数下去的，是计数单位的累加。由此，迁移到分数，也是按照分数单位依次往下数，是分数单位的累加。分数其实就是由若干个分数单位累加形成的，从线段模型中还可以清楚地看出四分之三是由3个四分之一累加得到的。这样的设计层次分明，有利于学生对分数单位的进一步理解，在头脑中形成了计数单位这一知识点的结构化体系。

有时为了达到更好的教学效果，需要教师设计合理有效的学习任务，结合有层次的反馈，给学生的思维带来新的挑战，形成对概念的全面认识，不断提高学习与思辨的能力。

教学设计应基于教材的逻辑起点、学生的认知起点等方面考虑，围绕教学重点、难点设计学习任务，为学生搭建一个开放的、自主的学习平台，让学生在个性表征、多元碰撞中，积累丰满的直观表象，形成概念的深度构建。