促进学生深度学习的“问题链”设计与思考

夏齐平 陈小燕

摘    要：数学教学旨在发展学生的数学核心素养.通过以问题链为脚手架的深度学习，诱导学生的思维发展，从而发展学生的数学核心素养.

关键词：深度学习;问题链;尺规作图

初中数学教学旨在发展学生的数学核心素养，而促使学生深度学习是培养核心素养的重要途径.深度学习是一种基于高阶思维发展的理解性学习.因此，教师设计有效的问题启发学生思考，是学生深度学习的重要形式.

浙教版八年级上册《1.6尺规作图》一课，是一节动手操作型作图课，日常教学都是以教师黑板演示，学生草稿纸上模仿，以这种灌输式的教学方式完成，缺乏学生思维的锻炼.这样的数学不是我们希望的，这样的数学是不能提升学生的数学核心素养的.在日常教学中尝试采用“问题链”的形式，开展《1.6尺规作图》的探索活动.

一、以问题链为脚手架的深度学习的理念

（一）深度学习的理念

深度学习的概念源于人工神经网络的研究，通过组合低层特征形成更加抽象的高层表示属性特征.不同学习领域可以呈现不同的深度学习形式，基于问题链的数学深度学习，是在表层数学知识认知的形势下进行数学思想的渗透，从思维的“深度”用全面的、联系的眼光进行数学教学设计，引导学生进行数学学习，这也符合新课改下的课程标准要求.

（二）“问题链”的内涵

“问题链”是问题设计呈现的一种结构形式，在数学问题中，把那些逐渐深化、层层递进、具有内在联系的问题联结起来，就形成“问题链”.“问题链”并不是简单罗列在一起的几个问题，而是为了实现教学目标，针对课堂教学过程中的重难点，将教材知识转化为层次分明、相互关联的一系列精心设计的问题.

（三）“问题链”设计的原则

“问题链”在教学环节的作用，不仅是诱導学生思考解决问题，也是激发学生的求知欲，提升学生解决问题的能力.设计“问题链”应有下列原则：

1.情景化原则.问题设计要有效，要能激发学生的求知欲，激发学生的兴趣和注意力，可以在情景创设的时候以实际问题的形式引入，从而激发学生的思考.

2.结构化原则.问题依据学生所学知识的特点，在知识覆盖面上尽量突出重点，体现一定的层次性，由表及里，由浅入深.由学生的最近发展区，发生认知冲突，激发学生的求知欲.

3.衔接性原则.“问题链”中的问题和问题之间的连接具有关联性，前一个问题能为后一个问题做铺垫，通过解决前一个问题时知识与方法的积累，指引我们解决后面的问题.

二、基于问题链的深度学习教学案例设计

（一）教学联结点

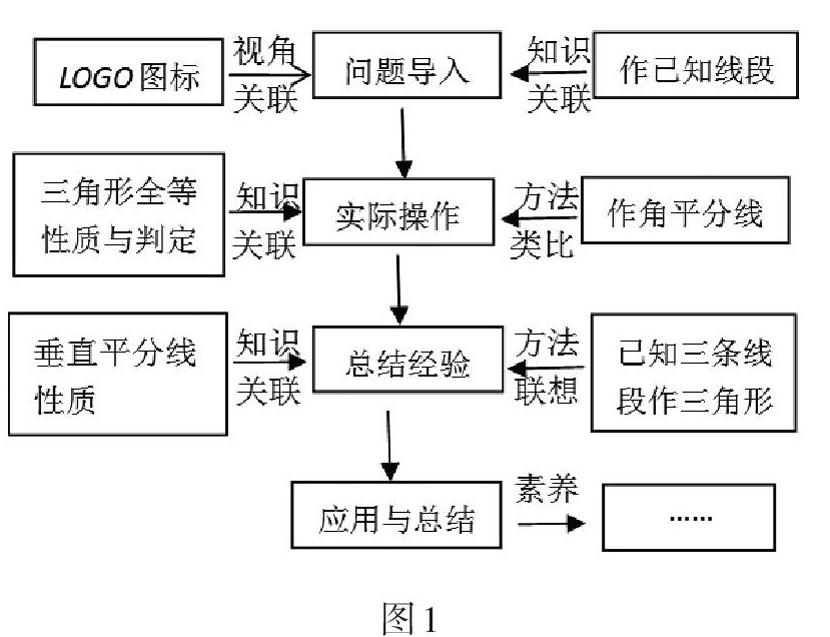
从知识角度上看，尺规作图是八年级上册第一章三角形的初步知识第六课.它是学习了三角形全等及判定定理，用尺规画一条线段等于已知线段、角平分线和已知三边画三角形等知识点之后，对几何作图的再探究.尺规作图和图形运动有密切的联系，是学生掌握图形运动的直观根据，是培养自主探究和动手实践的能力，几何直观素养和严密逻辑思维的重要载体（详见图1）.

（二）问题链的设计

问题1：我们在之前已经用尺规作过哪些图形呢？

问题2：在作一条线段等于已知线段时，直尺和圆规的作用是什么？

问题3：在作角平分线时，利用尺规画图的实质是什么？

问题1和问题2通过学生已有知识回顾，让学生感到尺规作图并不陌生，同时回顾尺与规在作图过程中的作用，分别是画线段和截长度;问题3为角平分线的尺规作图实质是构造了一对全等的三角形，从而类比作图方法，为学习新授课奠定方法基础.

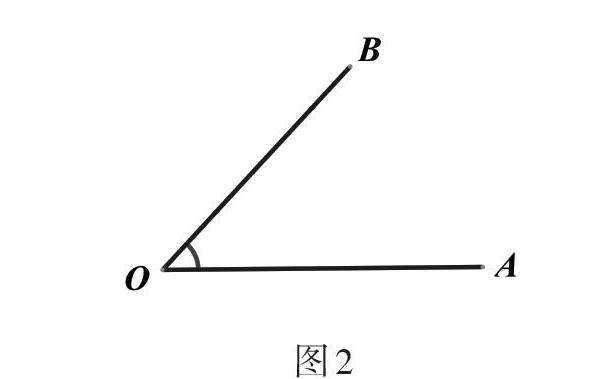
问题4：如图2，现在请在自己的草稿纸上任意画一个∠AOB，然后同桌互换，你能在空白处作一个∠A'O'B'，使∠A'O'B'=∠AOB吗？

问题5：你是怎么做出来的？你是怎么想的呢？

问题6：小组讨论一下，如何通过构造包含一个已知角的三角形和包含要求角的三角形全等？请代表说说看.

问题4和问题5通过学生的不断尝试，及小组合作交流，从而探索得到画一个角等于已知角的一般步骤，让学生充分体验探究的整个过程.问题6体验猜想到验证的逻辑过程，学会合作与交流，激发思维的发散过程.

问题7：如何说明∠AOB=∠A'O'B'？

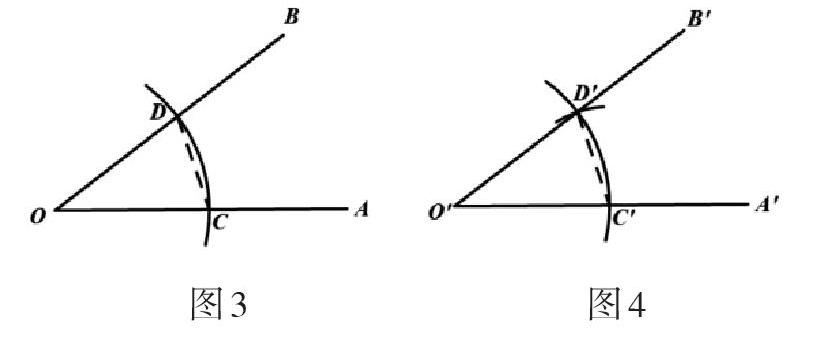
证明：如图3和图4，联结CD，C'D'.

∵在△OCD与△O'C'D'中，

OC=O'C'（作法）

OD=O'D'（作法）

CD=C'D'（作法）

∴△OCD △O'C'D'（SSS）

∴∠AOB=∠A'O'B'

问题7从作图的探索到推理的验证过程，是符合数学的一般探索规律，是培养学生思维的严密性的需要.

问题8：在学习三角形全等判定1时，我们利用尺规做出已知三条线段的三角形，我们还可以依据哪些条件作三角形呢？你能解决以下问题吗？

（1）如图5，已知∠1，∠2，线段a，用直尺和圆规作△ABC，使∠A=∠1，∠B=∠2，AB=a.

（2）如图6，已知：线段a，b，∠1，求作：△ABC，使BC=a，AB= b，∠ABC=∠1.

问题8通过引导学生在不同条件作三角形，拓展提高学生对作一个角等于已知角的应用能力.

如图7，已知线段AB，你能用直尺和圆规作线段AB的垂直平分线吗？

问题9：如图8，垂直平分线具有什么样的性质？你能利用圆规找到两个点来确定这条直线吗？

问题10：如图9，直线MN表示一条公路，点A、B表示两个村庄.现要在公路MN上建一个加油站，并使加油站到两个村庄A，B的距离相等，加油站应建在何处？在图上标出加油站的位置，并说明理由（画出图形不写作法，保留作图痕迹）

问题9通过问题链的设计，诱导学生思维的深度思考，从而分解降低本节课的难点;问题10通过实际问题的应用，进一步巩固并提高学生的应用能力.

三、基于问题链的深度学习反思

（一）问题设计有层次，思维锻炼在提高

尺规作图教学基于学生已有知识的最近发展区出发，从生活中随处可见的商标LOGO引入，能有效激发学生的学习兴趣，展示生活处处有数学，数学来源于生活;再从数学历史文化中古希腊人对尺规作图追求，展示学习数学几何的魅力;然后到作已知线段和角平分线的尺规作图回顾，从方法和作图经验上为学生学习本节课做好有效的铺垫;通过学生的个人尝试和小组合作的探索过程，有效分解本节课的难点“用尺规作已知角”，再求一个角等于两个角的和，巩固所学知识;通过已知条件作三角形，拓展了“用尺规作已知角”的应用能力;依据线段垂直平分线的性质，再次利用尺规构造全等三角形，提升尺规作图的能力;最后，通过师生的共同小结，梳理知识脉络，形成知识体系，提升思维能力.

（二）课中生成有落地，深度学习在达成

在课中生成中，本节课在设计问题链时，已充分考虑学生的学情，但在实际教学过程中，学生落实起来还是有一定的困难.主要集中在对作一个角等于已知角的探索中，虽然在课前的问题情景和经验回顾中始终强调的是“尺规”，但学生尝试作一个角等于已知角时，学生还是习惯用量角器去量和画，而没有借“尺规”尝试，存在一定的畏难情绪，于是，教师再次强调要求“尺规”作图中，是没有量角器工具的，并开展小组合作再次尝试;接着，小组合作过程中，再次与学生回顾“作角平分线”时，建立构造一对全等三角形的经验，学生运用经验性模仿，构造全等三角形，小组合作做出图形.

学生用尺规作图做出图形，教师在肯定学生的作图时，再次提出通过三次截长度画弧是能满足全等的条件的，建议再减少点次数鼓励学生画出图形.通过对比前后作图，比较得出这样的作图更简洁美观.

（三）课后纵深挖掘有延伸，教学反馈要及时

数学教学既包括课前的引导、课中的知识讲解及运用，还包括课后对数学问题解决过程的反思与回顾.通过及时的反馈使学生的元认知能力得到更高層次的发挥，课后摆脱“范例”式的题海战术，重视针对性的深度练习，做到及时反馈，以减轻学生负担，从而提高教学质量.例如，设置综合性的尺规作图题，让学生综合性地体会这方面的知识.

两个城镇A，B与一条公路CD，一条河流CE的位置如图10所示.某人要修建一避暑山庄，要求该山庄到A，B的距离必须相等，到CD和CE的距离也必须相等，且在∠DCE的内部，请画出该山庄的位置P（不要求写作法，保留作图痕迹）.

通过“问题链”的设计，诱导学生的思维发展，让原本学生以模仿为主的实践课有了思维的探索过程，从而发展学生的数学核心素养，真正体现了“以学为中心”“以生为本”的教学理念。