基于随机分布与高斯分布数据集的不同距离下的FCM 算法比较

焦存德

（阳泉师范高等专科学校数学系， 山西 阳泉 045200）

1 序言

聚类是根据一定的标准 （通常是距离标准）将一个数据集划分为不同的类， 使类内的相似性尽可能大， 类间的差异性尽可能大。 FCM（Fuzzy C-means） 聚类是一种与数据挖掘、 模式识别等研究方向相关的重要研究内容之一。 聚类算法的聚类结果是不可预测的。 在实际应用中，应根据数据类型选择合适的相似度测量方法， 便于有相对更合适的聚类效果［1］。 当然不一样的相似性度量方式又对应着不一样的距离准则， 所以研究不同距离下的FCM 算法比较有着重要意义［2-4］。

2 正文

设X=（x1， x2， …， xn）， b=（y1， y2， …， yn）为被分类对象的全体， 设每一组对象由一组特征数据 （xi1， xi2， …， xim） 来表征。 X 的模糊c-划分指的是由模糊c-划分矩阵A=（A1， A2， …，An）T=（aij）cn， aij∈［0， 1］

决定的划分{Ai|i=1， 2， …， c} 的划分， 满

所有模糊c-划分组成模糊c-划分空间。

最优模糊c-划分使下面的J（A， V） 取得最小值：

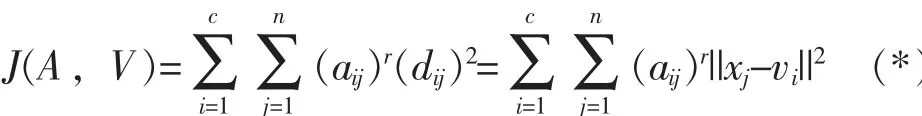
其中， 参数r 不小于1， r 越大分类越模糊；vi是Ai类的聚类中心， 定义为

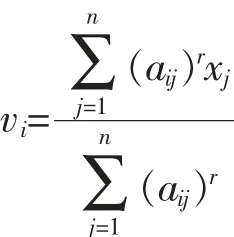
构造下面的目标函数， 可得到 （*） 式达到最小值的必要条件：

记

这里λj， j=1， 2…n 是（*） 的n 个约束式的拉格朗日乘子［5］。

对所有参变量求导， 是 （**） 达到最小值的必要条件为

则J （A， V） 取得最小值， 即此时可得到最优模糊c-划分。

（2） 当距离标准为曼哈顿距离时， 则J （A，

得最小值， 即此时可得到最优模糊c-划分。

得最小值， 即此时可得到最优模糊c-划分。

（4） 当距离标准为闵可夫斯基距离时， J （A，

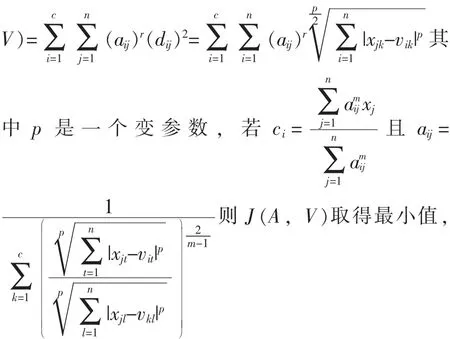
即此时可得到最优模糊c-划分。

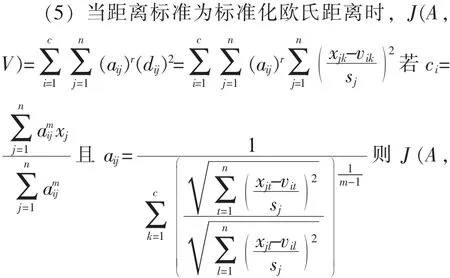
V）取得最小值， 即此时可得到最优模糊c-划分。

J（A， V） 取得最小值， 即此时可得到最优模糊c-划分

则J（A， V）取得最小值， 即此时可得到最优模糊c-划分

通过上面的分析我们可以得到FCM 算法是一个简单的迭代过程。 所以在实现Matlab 仿真时， 我们采用迭代算法。 在Matlab 中， 已经有基于欧氏距离的FCM 算法， 我们查找到了该程序的源代码， 并找到其中决定算法结果的距离函数， 将其先后替换为前文中提到的几种距离， 进行了实验分析仿真。 同时， 我们聚类的对象有两个， 一是随机分布的数据， 一是高斯分布的数据。 对这两种数据的聚类算法分别如下：

（一） 基于随机分布的数据的最优c-划分

步骤1： 产生随机分布的数据， 即随机数；

步骤2： 任选c 个数据对象为初始类中心，

步骤3： 重复

①计算每个数据到各类中心的距离， 并将其分配到距离最小的类中；

②计算新的类的中心 （可以不是被聚类的数据）， 直到J（A， V） 相对上次J（A， V） 的改变量小于某个阀值 （在本文中我们选择该值为10-5）， 则循环停止；

步骤4： 绘图， 使聚类结果更直观地表现出来。

本文将采用的实验方法基于随机生成的随机分布的二维数组 （共生成20 组）， 分别使用上述7 种距离对每组测试数据采取FCM 聚类， 同时记录在不同距离下的聚类结果， 利用统计方法分析比较了聚类方法在7 个距离下的性能。 下图为同一组测试数据在聚类数c=2 或3 下的聚类结果。

图1 c=2 时7 种距离下随机数据的聚类结果

图2 c=3 时7 种距离下随机数据的聚类结果

当c=2 时， 根据同一点的分布区域的特点，本文对20 个测试数据集进行了聚类。 结果分为4类， 分别定义为A 类、 B 类、 C 类和D 类， 每种类型的分布如图3 所示。

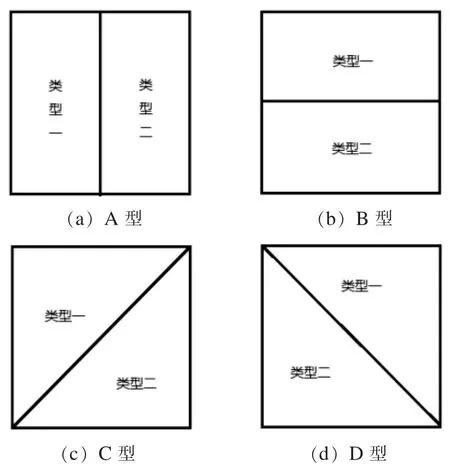
图3 c=2 时聚类结果的4 种类型

同样， 当测c=3 时， 所有20 个测试数据集的聚类结果根据其概括根据相似点的形状的不同， 可分为6 类， 分别被定义为类型A、 B、 C、D、 E、 F， 其分布图如图4 所示。

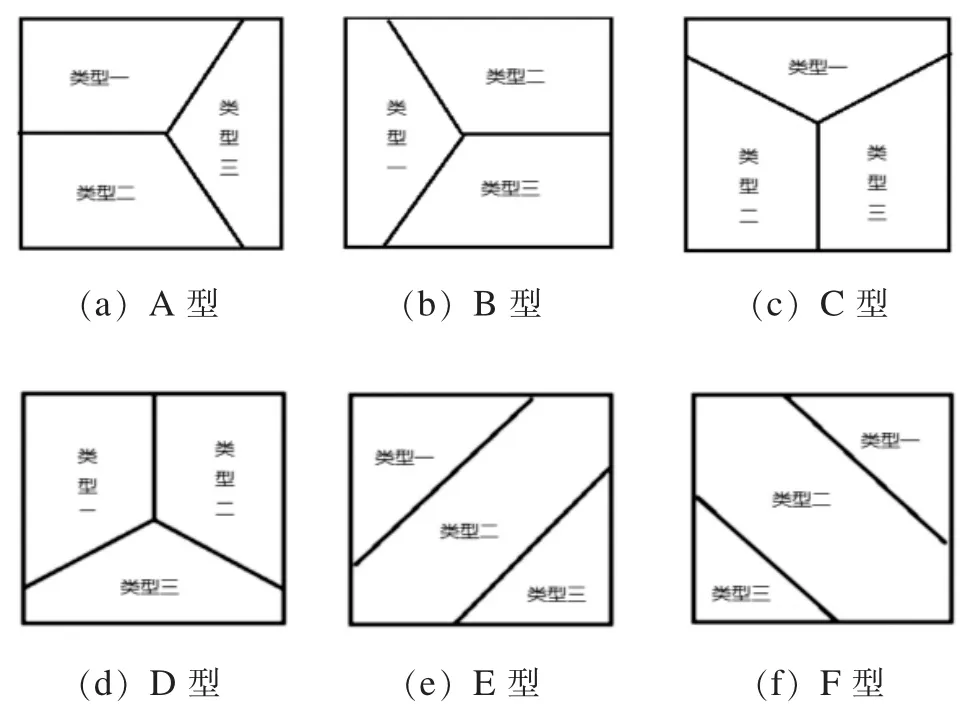
图4 c=3 时聚类结果的6 种类型

根据上述分类方法， 对所有测试数据的聚类结果进行分类并记录。

表1 不同距离下的FCM （c=2） 聚类结果统计

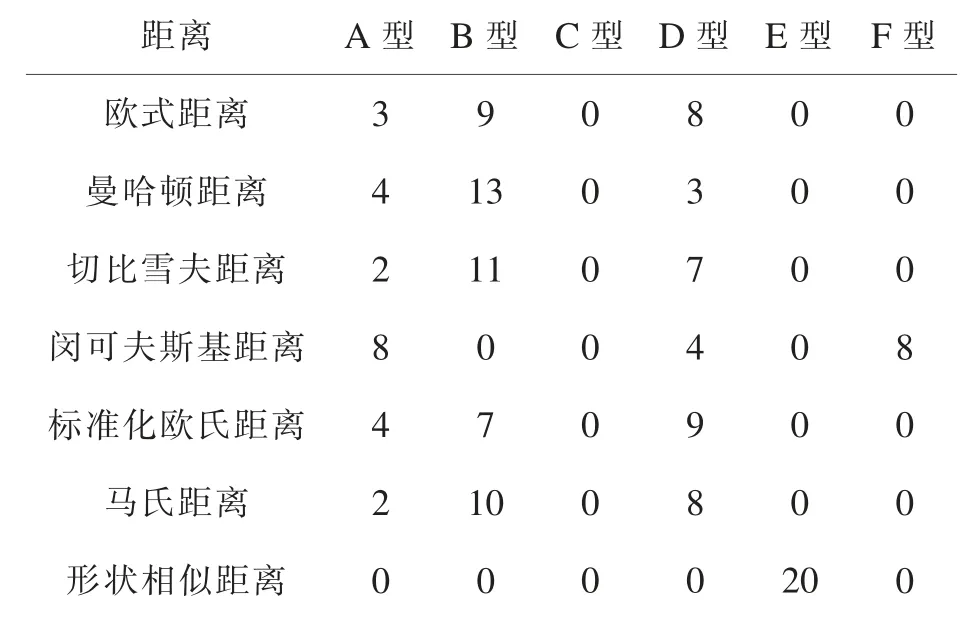
表2 不同距离下的FCM （c=3） 聚类结果统计

表1 和表2 表明无论聚类分类数是2 或3，所有依据形状相似距离为聚类结果的都归为同种类型中。 因此形状相似距离在解决基于随机分布的数据的最优c-划分的问题更有优势。

（二） 基于高斯分布的数据的最优c-划分

仿照随机分布的实验方法， 在这一部分， 我们用MATLAB 产生高斯分布的二维数组作为测试数据（共生成20 组）， 用标准FCM 聚类算法，分别采用7 种距离对每组测试数据采取FCM 聚类， 同时记录在不同距离下的聚类结果， 利用统计方法分析比较了聚类方法在7 个距离下的性能。 本文规定分类数c=2 或3。

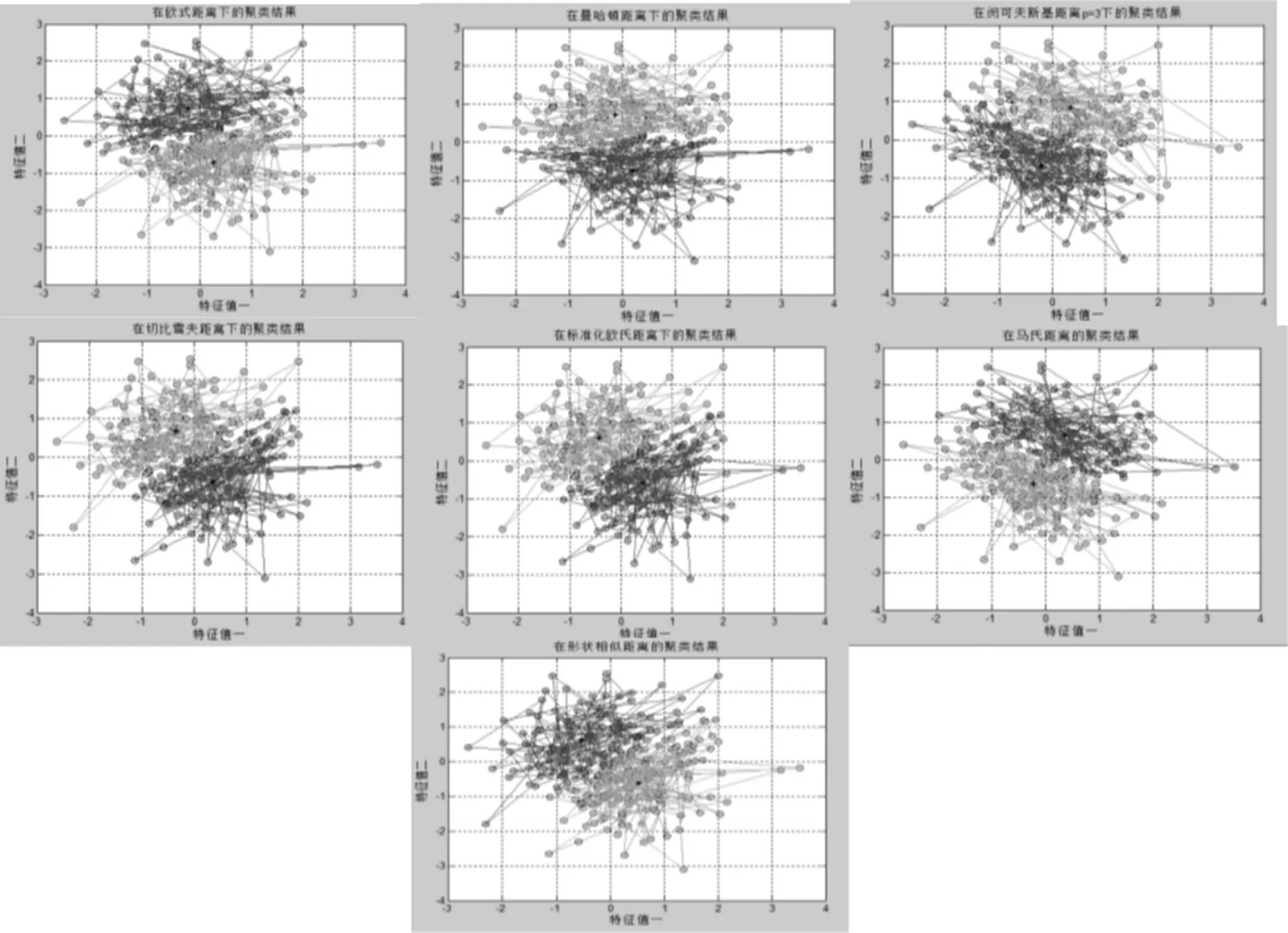
图5 c=2 时7 种距离下高斯分布的聚类结果

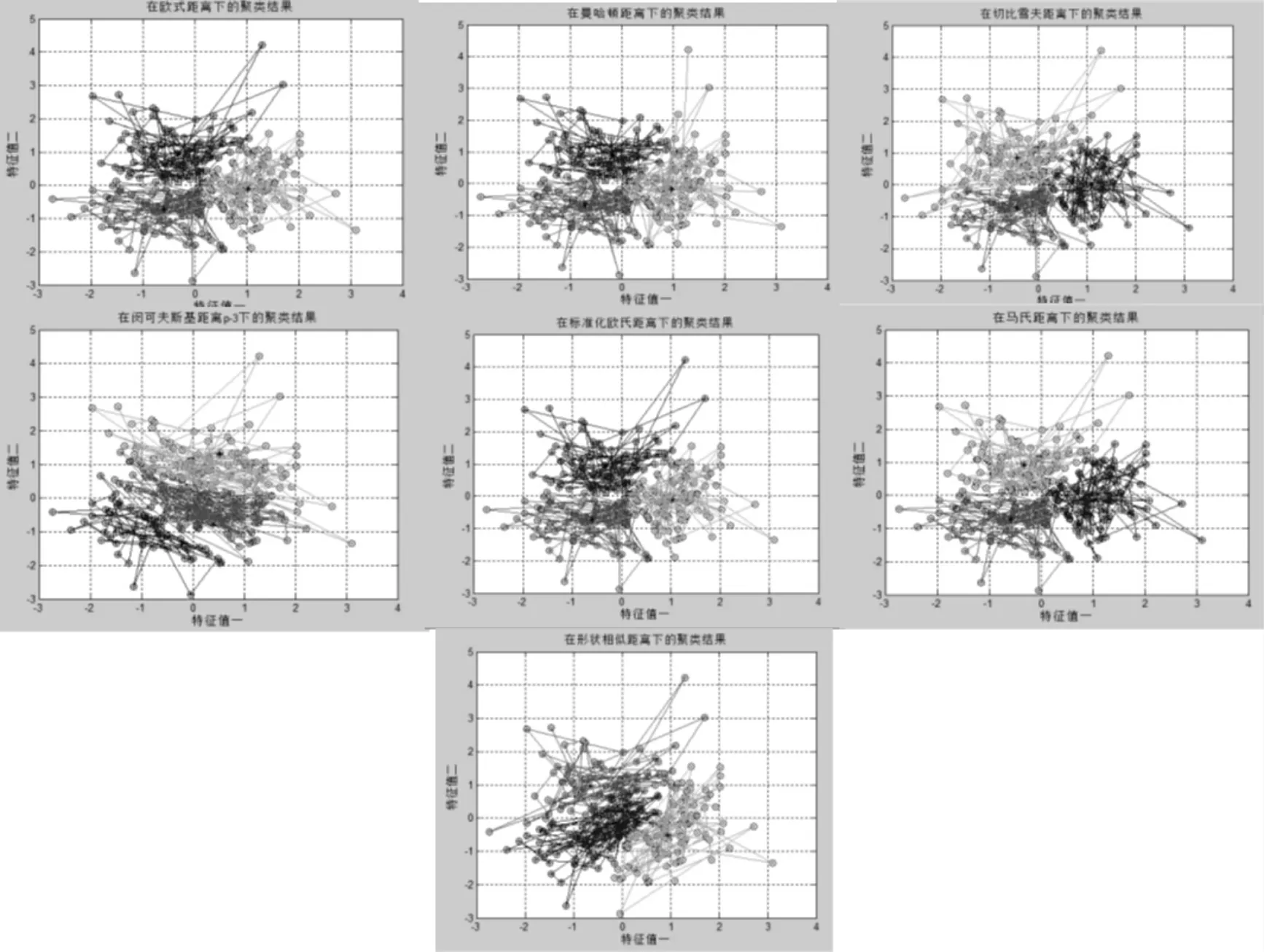
图6 c=3 时7 种距离下高斯分布的聚类结果

（3） 结果分析

由上面的图5 和图6 可以看到无论是c=2 还是3， 不同距离下的高斯分布数据集的聚类结果并无大差异。

3 结论

本文给出了欧式距离、 曼哈顿距离、 切比雪夫距离、 闵可夫斯基距离、 标准化欧式距离、 马式距离和形状相似距离的FCM 算法公式。 为了比较这些算法的好坏， 我们使用Matlab 本文的算法应用于两种类型的数据分别进行聚类， 并分析结果。 本文的主要结论是当数据是随机分布的，形状相似性距离可分为结合对象大小和形状相似性的两个因素。 因此， 在这种情况下， 形状相似的距离比其他距离更合适。 然而， 不同距离的高斯数据集聚类结果没有显著差异。