山岭隧道地下水限量排放方案参数研究

陈 鹏 刘柏林

（湖北省交通规划设计院股份有限公司， 湖北 武汉 430051）

1 工程简介

小北山1# 隧道按左右线分离式布置， 左线起迄桩号为ZK14+390～ZK17+390， 长3000m； 右线起讫桩号为K14+380～K17+388， 长达3008m， 属特长隧道， 是揭惠高速的控制性工程之一。

经勘探， 在隧道分布范围内有三条断裂带，其中F3 断裂带位于小北山1# 隧道ZK16+450～ZK16+600 左侧与龙潭峰水库连接， 该位置围岩破碎， 裂隙发育。 龙潭峰水库建成于1960 年，由普宁市麒麟镇管理， 其作用涵盖防洪、 灌溉、供水及发电， 支撑着麒麟镇农业生产和经济发展， 至今运行正常， 若遭受破坏， 将对下游镇上人民的经济及财产安全造成重大影响。

图1 所示为隧道与水库的相对位置关系图，两者水平距离约100m， 竖直方向上， 水库水位高于隧道设计高程约150m。 由于隧道与水库经F3 断裂带连通， 若采取完全堵水， 水库将会对隧道产生巨大水压力， 使工程建设成本提高，并且造成安全隐患。 若采取全排措施， 则会影响龙潭峰水库的蓄水量， 影响周边居民生活。故此， 为保护该处水资源， 并防止隧道出现塌方、 涌水等灾害， 计划对该隧道采取限制性防排水措施。

图1 龙潭峰水库与小北山1# 隧道相关位置关系图

预测隧道涌水量是设计隧道限制性防排水方案的前提， 在隧道涌水量预测与限制性防排水方面， 国内外学者已经做出了大量的研究。 早在20世纪50 年代， 日本学者高桥彦治［1］首先总结出一套简单的隧道涌水量计算方法， 而后越来越多的学者在此基础上对隧道涌水量预测进行研究。针对于工程项目的可行性研究和初勘阶段， 中国学者朱大力［2］从大气降雨、 隧道集水面积角度考虑， 提出采用降雨入渗法对隧道进行涌水量预测。 此外， 聂志宏［3］等结合工程实际， 总结并检验了国内外多种预测用水量方法。 对于隧道的防排水技术， 吕康成和崔凌秋［4］在隧道防排水工程指南一书中进行了归纳总结。 而且由于近年来水下隧道的增多， 相应的防排水规范也越来越成熟［5］。 结合厦门翔安海底隧道， 王秀英、 王梦恕、 张成平等得出了许多研究成果， 提出限制性防排水需先确定合理水压力， 并以此作为防排水方案的依据［6～8］。

2 隧道水文试验

为探明隧址区水文情况， 布置6 个钻孔对地下水水位进行勘察， 依次编号SZK1-SZK6。 根据现场的实际情况， 选取SZK2 和SZK6 两个钻孔来进行注水试验， 选取SZK3 进行抽水试验。以下为试验结果。

实测钻孔地下水稳定水位见表1， 注水试验及抽水试验成果分别见表2、 表3。

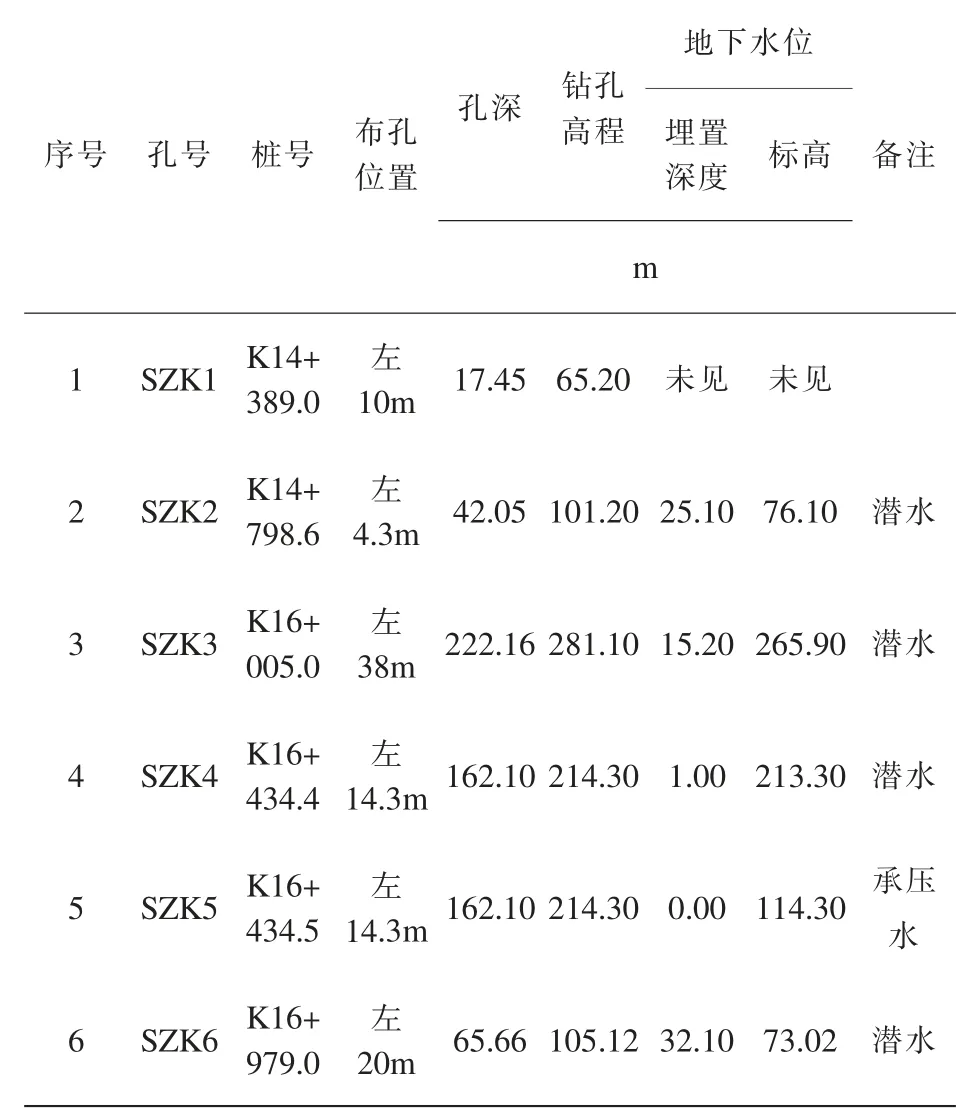
表1 钻孔地下水稳定水位一览表

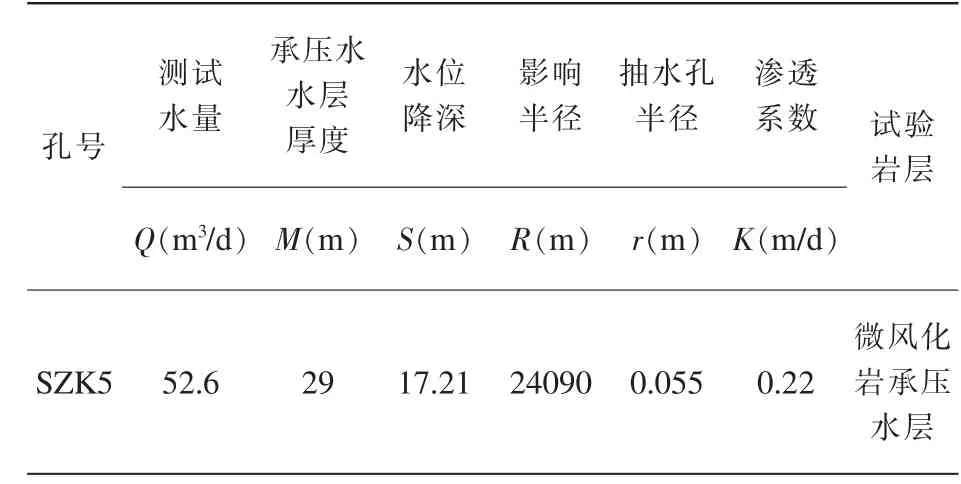
表2 降水头注水试验数据成果表

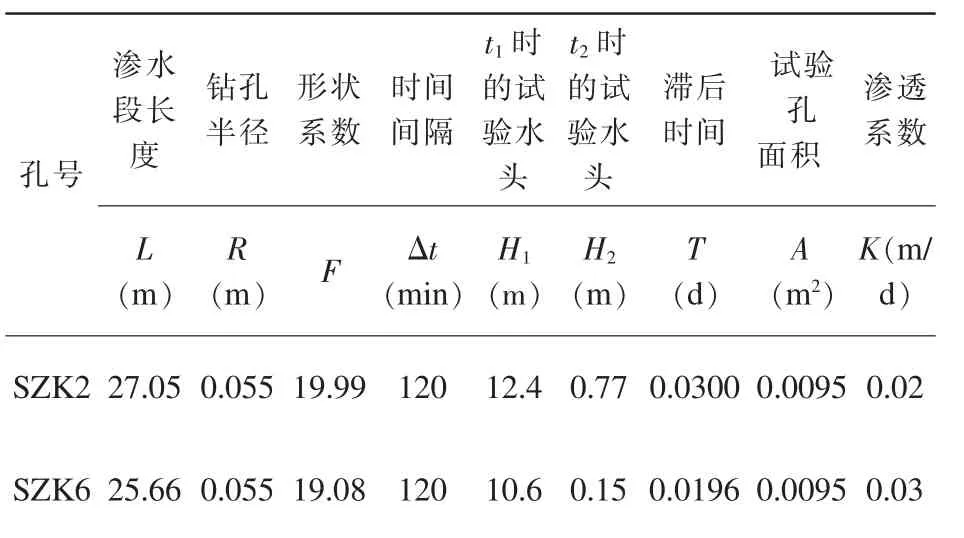
表3 抽水试验数据表

3 隧道涌水量预测

根据试验结果， 采用降雨入渗法和稳定流理论公式法两种方法对隧道涌水量进行预测。 其中， 根据降雨入渗法来计算隧道涌水量的经验公式见式 （1）。

式中： Q—预测涌水量， m3/d； T—降雨入渗系数； W—年均降水量， mm； A—隧道工程集水面积， km2。

查阅相关资料及参照隧道所处地区类似工程经验， 可取降雨入渗系数T 为0.25； 年均降雨量W 为1800mm； 隧道集水面积A 为6.5km2； 依此计算出隧道涌水量结果如表4 所示。

表4 隧道涌水量计算成果表

采用稳定流理论公式法， 要根据潜水部分和承压水部分对隧道进行分段预测。

其中， 潜水部分的隧道涌水量预测计算公式见式 （2）：

对于承压水部分的隧道涌水量预测计算公式见式 （3）：

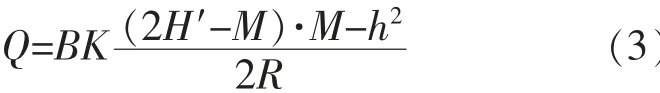
式中： Q—单洞涌水量m3/d； B—隧道穿越水层距离， m； K—水层渗透系数 （平均值）， m/d；H—隧道上方水层厚度 （平均值）， m； H′—承压水底部与地下水位距离， m； M—承压水水层厚度 （平均值）， m； h—隧道边墙位置水位高度，取为0m； R—排水影响范围的宽度， m。

根据水文试验的结果， 采取稳定流公式法所 得到的隧道涌水量预测值见表5。

表5 隧道涌水量计算成果

根据计算结果可见， 降雨入渗法所得的隧道双洞涌水量预测值为8014m3/d， 采用稳定流理论公式所得的隧道双洞涌水量预测值为7880m3/d，极差不到2%。 说明所得预测值对实际工程具有参考价值， 故取两者平均值7947m3/d 进行后续研究。

4 限制性防排水参数分析

限制性防排水的主要问题是处理好排水量与衬砌水压力的关系， 其主要的构造为排水管、 衬砌、 防水层、 二衬和注浆圈。 为方便研究， 将隧道模型简化如图2 所示。 将隧道断面近似当作圆形处理， 水头高度取为H， 衬砌内径、 外径分别记为R0、 R1， R2为最远短距离， 和H 相等， 注浆圈半径记为Rg。

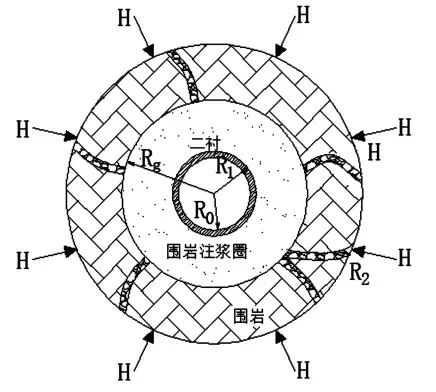
图2 排水量与水压力关系简化计算模型

将围岩、 浆体、 二衬的渗透系数依次记为kr、 kg、 k1， 由此模型得出的隧道衬砌外水压力公式见式（4）。

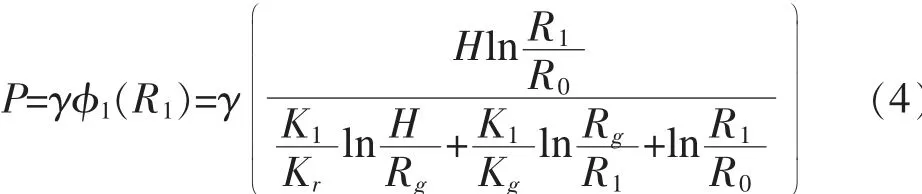
根据现场情况， 将隧道围岩渗透系数取值为kr=0.22m/d， 隧道衬砌等效内径、 外径分别取为R0=6m、 R1=6.5m， 隧道单洞涌水量取值为Q=3974m3/d。

（1） 对浆体渗透系数的研究。

采用控制变量法， 先选定厚度为6 米注浆圈作为研究对象， 改变浆体渗透系数， 观察水压力与排水量之间的关系。 计算中依次选取的浆体渗透系数为kg=0.11m/d， kg=2.2×10-2m/d， kg=7.3×10-3m/d， kg=4.4×10-3m/d， kg=3.1×10-3m/d， kg=2.2×10-3m/d， kg=1.5×10-3m/d， kg=7.3×10-4m/d。 为表达简便，令n=kr/kg， 则n 值依次为2， 10， 30， 50， 70，100， 150， 300。 得到的计算结果如图3 所示。

根据工程经验及规范要求， 需控制本工程水压力不超过800kPa。 根据图3 所示结果， 当注浆圈厚度为6 米时：

若n=70， 即浆体渗透系数为3.1×10-3m/d时，排水量Q 需不小于7m3·d-1·m-1；

若n=100， 即浆体渗透系数为2.2×10-3m/d时， 排水量Q 需不小于5m3·d-1·m-1；

若n=150， 即浆体渗透系数为1.5×10-3m/d时， 排水量Q 需不小于4m3·d-1·m-1；

若n=300， 即浆体渗透系数为7.3×10-4m/d时， 排水量Q 需不小于2m3·d-1·m-1；

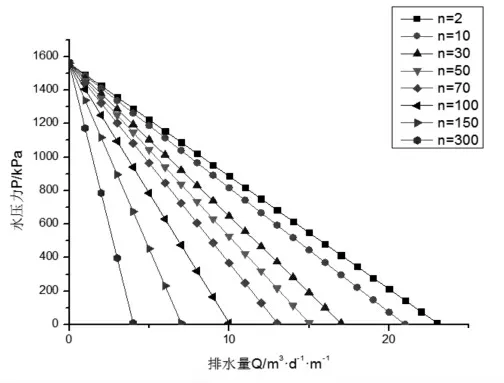
图3 不同浆体渗透系数衬砌水压力与排水量关系曲线

（2） 对注浆圈厚度的研究。

选定浆体渗透系数为1.5×10-3m/d， 改变注浆圈厚度， 观察水压力与排水量之间的关系。 计算中依次选取的注浆圈厚度D=5m， 6m， 7m， 8m，9m。 得到的计算结果如图4 所示。

根据工程经验及规范要求， 需控制本工程水压力不超过800kPa。 根据图4 所示结果， 当浆体渗透系数为1.5×10-3m/d 时：

若注浆圈厚度D=5m， 排水量Q 需不小于6m3·d-1·m-1；

若注浆圈厚度D=6m， 排水量Q 需不小于4m3·d-1·m-1；

图4 不同注浆圈厚度衬砌水压力与排水量关系曲线

若注浆圈厚度D=7m， 排水量Q 需不小于3m3·d-1·m-1；

若注浆圈厚度D=8m， 排水量Q 需不小于3m3·d-1·m-1；

若注浆圈厚度D=9m， 排水量Q 需不小于2m3·d-1·m-1；

根据以上所得结果， 结合小北山1# 隧道实际情况， 综合考虑环境保护、 工程质量与成本问题， 隧道限制性防排水相关参数最佳取值为浆体渗透系数kg=1.5×10-3m/d， 注浆圈厚度D=6m， 排水量为Q=4m3·d-1·m-1。

5 结论

根据水文试验结果， 采用两种方法来预测隧道涌水量， 所得预测值分别为8014m3/d 和7880m3/d， 极差不到2%， 计算结果对实际工程具有参考价值。

从限制性防排水相关参数的研究过程中可以看出， 衬砌水压力与排水量、 浆体渗透系数以及注浆圈厚度等参数紧密相关， 当浆体渗透系数与注浆圈厚度确定时， 衬砌水压力随着排水量增大而线性降低， 直至变为0。 而该线性关系曲线斜率与浆体渗透系数及注浆圈厚度相关， 当浆体渗透系数越小， 注浆圈厚度越大， 关系曲线斜率均变大， 反之则相反。

经研究， 小北山1# 隧道限制性防排水相关参数最佳取值为浆体渗透系数kg=1.5×10-3m/d，注浆圈厚度D=6m， 排水量为Q=4m3·d-1·m-1。

经检验， 采用该方案后， 龙潭峰水库水位略有降低， 但对其使用功能未造成影响， 隧址区的生态环境也没有明显破坏， 隧道质量也达到工程要求。