基于改进BBO算法优化KELM的短期风电功率预测

任瑞琪

(西安铁路职业技术学院 牵引动力学院，陕西 西安 710026)

0 引言

近年来，风力发电大规模发展，带来的问题也随之出现，风力发电的随机性和波动性给其集成带来了一定的限制。解决这一问题的方法之一是对风电场的输出功率进行预测，有利于提高电力系统的稳定性[1-2]。

近年来，许多学者将更先进的BP神经网络[3]、支持向量机[4]、极限学习机[5]等方法引入传统的基于统计与学习方法的风电功率预测中。对于传统的基于梯度学习的迭代学习方法带来的过度训练、泛化性能差以及易陷入局部最优的问题，Huang等[6]提出了一种基于单隐层前馈神经网络的快速特殊学习方法(Single-Hidden Layer Feedforward Neural Networks，SLFNS)、极限学习机(Extreme Learning Machine，ELM)。ELM随机选取隐含层神经元的输入权重与偏置并采用简单的矩阵运算得出输出权重。由于通过正则化最小二乘算法调节输出矩阵，因而具有更迅速的训练速度与更优异的泛化性能。王焱等[7]提出了一种基于Bootstrap和OS-ELM的超短期风电功率预测方法，黄庭等[8]提出了一种基于小波—极限学习机的短期风电功率预测方法。Huang等[9]给出了一种ELM结合核学习方法的新型核极限学习机算法。核极限学习机(Kernel Extreme Learning Machine，KELM)是将ELM的隐含层节点映射取代为核函数映射，从而避免了初始权值与偏置对其精度的影响，并在结合ELM与核方法之后表现出训练简便与泛化性能好的优点，广泛应用于分类与回归领域。

近年来，许多优化算法被应用于核极限学习机的参数与输入结构的优化，用以寻找最优的参数与输入结构，提高了学习精度与预测效果。杨锡运等[10]提出了一种基于粒子群优化的核极限学习机模型的风电功率区间预测方法，李军等[11]在风电功率预测中应用遗传算法(GA)、微分演化(DE)、模拟退火(SA)3种算法优化的KELM方法。Dan[12]提出了一种描述生物物种在地理学分配上的优化算法，即具有良好的鲁棒性与寻优速度的生物地理学优化算法(Biogeography-Based Optimization Algorithm，BBO)。Kong等[13]用混沌映射改进提升了蜂群算法(Bee Colony Algorithm，BCA)的性能。针对BBO算法易陷入局部最优的问题，Saremi等[14]提出了基于混沌映射理论的BBO优化算法，在Ma[15]的基础上，针对KELM的优点，基于余弦迁移模型，本文提出了一种改进的BBO优化核极限学习机的(BBO-KELM-2)预测方法，对核极限学习机的输入结构，核参数γ与正则化系数η进行优化后应用于不同地区的风电功率预测中，并与采用线性迁移模型的原始BBO-KELM-1等方法在同等条件下进行比较，已验证该方法在风电功率预测方面的有效性。

1 BBO优化算法

在BBO算法中，每一个优化问题的候选解的所有特征组成的向量即栖息地称为适应度指数向量(Suitability Index Vector，SIV)，每一个栖息地中的物种即候选解的特征称为适宜度指数变量(Suitability Index Variables，SIVs)，栖息地与居住者(物种)相当于遗传算法中的染色体与基因。栖息地适应度指数(Habitat Suitability Index，HSI)是衡量一个栖息地的适宜度的指标，高HSI值表示该栖息地的种群数目多[16]。

1.1 迁移操作

线性迁移模型描述物种数目与迁移概率的关系，栖息地中物种数目的Ch与迁入概率λh和迁出概率μh的线性关系数学模型由式(1—2)给出。

(1)

(2)

其中，I和E分别是迁入率函数的最大值和迁出率函数的最大值。

1.2 变异操作

突变概率可通过式(3)计算。栖息地的突变概率mh与其物种数量概率Ph成反比，即：

(3)

其中，Ph为栖息地中物种数量为Ch时所对应的概率，Pmax为Ph的最大值，M为用户定义的突变率最大值。

2 改进的BBO优化算法

2.1 迁移模型的改进

Ma[16]通过对实例进行研究，结果选出的余弦迁移概率模型为更符合自然界生态系统中复杂规律的物种迁移模型。因此，本文在BBO算法中引入余弦迁移模型。余弦迁移模型对应的迁入率λk与迁出率μk分别为：

(4)

(5)

2.2 引入混沌映射理论

BBO算法在运行时，容易陷入局部极小，收敛速度也会降低，因此引入混沌映射理论，具体操作为在进化到第g代时，进化过程中确定各栖息地的初始迁入概率的随机值可通过式(6)所示的正弦混沌映射得到值C(g)来代替[17]。

(6)

3 BBO-KELM方法

3.1 KELM方法

包括输入层、隐含层与输出层3个分层的ELM是一种特殊的单隐层前馈神经网络。对于N组训练样本数据集(xj,tj)∈Rn×Rm，当ELM的隐含层节点数为L，并且激励函数为ϑ时：

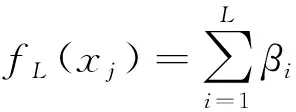
(7)

其中，第i个隐含层节点和输出层节点之间的权值向量为βi。ELM完全不同于传统的迭代学习算法在于它在分析计算出输出权值β的最小二乘解之前随机选择隐含层节点的输入权值ω与偏置b，之后。降低训练错误率并优化泛化能力是这些运算所能达到的目的。

根据ELM理论，将式(7)重新写为紧凑的格式：

Hβ=T

(8)

对于一个训练数据集，在给予激励函数与隐含层节点数之后，以下3步为ELM的训练过程。步骤1：随机产生输入权值ωi与偏置bi，1≤i≤N；步骤2：计算隐含层的输出矩阵H；步骤3：计算输出权值矩阵β=H+T；

其中，H+为隐含层输出矩阵H的Moore-Penrose广义逆。当HHT为非奇异时，H+=HT(HHT)-1。

为了消除“病态矩阵”的结果误差，按照岭回归的思想，引入正则化系数η，则网络输出权值的最小二乘解为：

β=HT(HHT+ηI)-1T

(9)

因此，相应的ELM输出函数为：

y(x)=h(x)β

(10)

在特征映射函数h(x)未知的情形下，在ELM中引入核函数，则可形成新的基于核的ELM(KELM)方法。

KELM方法中，需定义核矩阵QELM=HHT，其元素为：

QELM(i,j)=h(xi)·h(xj)=K(xi,xj)

(11)

那么借助式(5)，网络输出可表示为：

(12)

式(12)中，本文选择核函数K(xi,xj)的类型为径向基核函数，即：

(13)

其中，γ为RBF核函数的核参数。

3.2 BBO-KELM方法

BBO-KELM方法主要优化网络结构，Tikhonov正则化系数η与RBF核参数γ。在O-KELM方法实现过程中，网络性能的好坏与适宜度评价函数成正比，即：

(14)

(15)

其中，ERMSE(y*,y)是均方根误差，方法的预测输出是y*(i)，实际输出是y(i)。

待优化的决策变量由实数变量与二进制变量组合而成，种群个体ah=[s1,…sn,γ,η]，h=1,2,…m由核参数γ与正则化系数η两个实数变量与网络结构输入的二级制变量构成，其中，模型的输入维数为n，种群个体的数目由m表示，二进制变量sa∈{0,1}，a=1,…,n决定模型的第j维输入是应保留还是舍弃。

(16)

将真实值为二进制数的个体h的第l个决策变量变换为整数型变量，即：

xhl=round(ahl)

(17)

其中，函数round(.)是指将变量四舍五入到最近的整数。具体应用时，需要通过式(16)对核参数γ与正则化系数η进行转化，这两个参数的取值范围γ∈[0,600]，η∈[0,100]。二进制变量sa,a=1,…,n，则需要通过式(17)进行转化。其次，需要将个体的决策变量转化为真实值之后再计算个体的评价函数。

改进BBO-KELM算法的实现流程如图1所示。

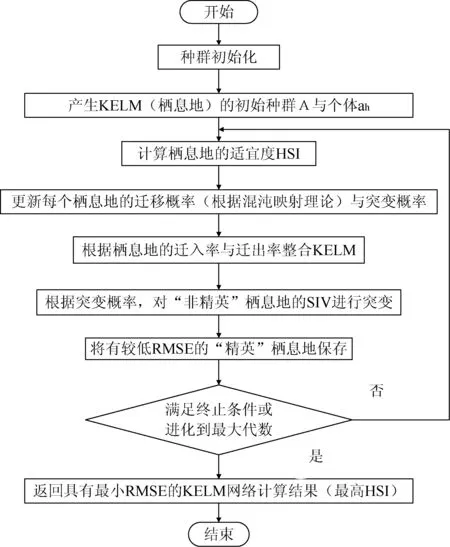
图1 改进BBO-KELM算法实现流程

4 实验仿真

4.1 建立预测模型

将提出的改进BBO-KELM算法即BBO-KELM-2算法应用于风电功率预测实验中，并在同等条件下与采用线性迁移模型的原始BBO-KELM-1算法以及PSO-KELM算法、GA-KELM算法、DE-KELM算法、SA-KELM算法等进行比较。本文采用时间序列建模的方式进行风电功率预测，即：

y(t+D)=f(xt),∀t=Δ…l

(19)

其中，D为预测步长，Δ表示嵌入维数，xt为历史负荷值(yt-1,yt-2,…,yt-Δ)。

优化方法中，初始化选取核参数与正则化系数的取值范围分别是γ∈[0,600]和η∈[0,100]，预测性能评价指标主要采用3种，分别是平均绝对误差(MAE)，平均绝对百分比误差(MAPE)和归一化均方误差(NMSE)。

(20)

(21)

(22)

其中，待预测时间序列各点的实际输出为y(i)，相应模型的预测输出为y*(i)，预测样本点数为N，待预测时间序列的方差为σ2。

4.2 风电功率预测实例

实验选用加拿大Alberta省一个月内某风电场的采样间隔为10 min的实测风电功率数据集，具体时间取原始数据的2010年12月5日—30日，对原始数据的连续3个样本进行平均，得到采样间隔为30 min的实验数据集。训练数据取该风电功率数据集的前1 000组，测试数据取剩下的200组，嵌入维数Δ=16。

实验中，O-KELM方法的初始种群数为100，最大进化代数为250。GA中的交叉概率pc为0.4，变异概率pm为0.1。DE中的尺度因子λ位于区间[0.5,2]。SA的初始温度为100，μ=0.95。BBO算法的Pmod=1，I和E均为1，突变概率mk=0.005，精英数量z为2。PSO算法中的惯性权重w=0.3，精英主义参数z为2，认知常数c1=1，群体相互作用参数c2=1，邻里相互作用参数c3=1。在O-ELM方法中，设置隐含层节点数初始化的最大值为L=200。隐含层节点数目L、正则化系数η在不同O-ELM方法下的选择情况以及核参数γ、正则化系数η在不同O-KELM方法下的优选结果如表1所示。不同方法的200组风电功率预测性能指标的结果对比如表2所示。

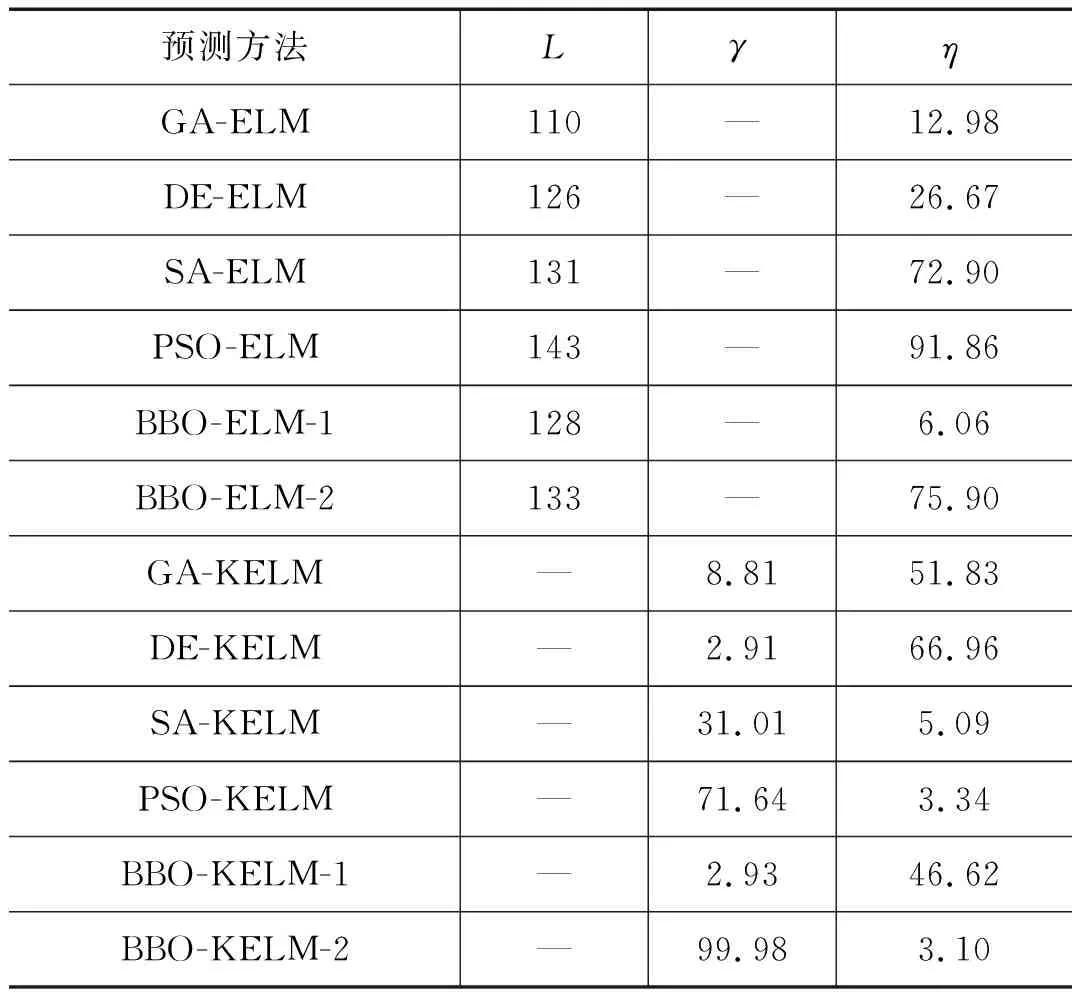
表1 O-KELM方法与O-ELM方法的参数选择对比

表2 BBO-KELM方法与其他方法的性能指标对比

由表2可见，在同等条件下O-KELM方法的两种性能指标MAPE和NMSE明显优于O-ELM方法，且经过改进的BBO-KELM-2算法具有更好的预测结果。

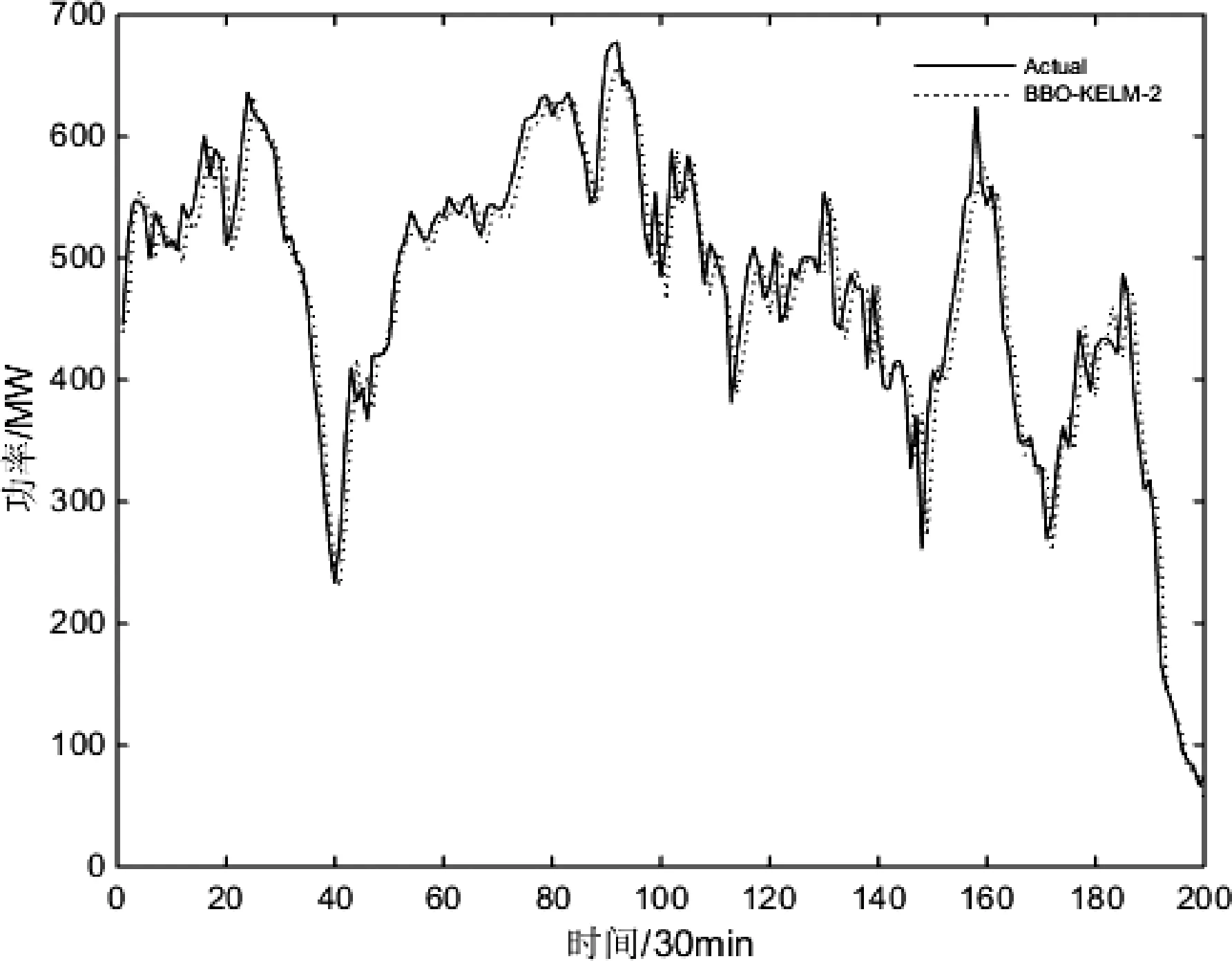
图2 BBO-KELM-2方法提前30 min风电功率预测的训练误差收敛曲线

图3 O-KELM方法提前30 min风电功率预测的训练误差收敛曲线

BBO-KELM-2算法预测的200组风电功率与实际功率的结果对比如图2所示，可以看出，BBO-KELM-2算法的预测性能较好，能较准确地预测实际风电功率。O-KELM 5种方法预测结果的训练误差收敛曲线如图3所示，可见，所提出的BBO-KELM-2方法具有最小的训练误差与更快的收敛速度。