三体船连接桥应力集中区域优化设计研究

汪 俊，李庆宇，黄立为，孙 昉，李伯林

(1.上海交通大学 海洋智能装备与系统教育部重点实验室，上海 200240；2.中国人民解放军陆军装备部驻沈阳地区军事代表局驻大连地区军事代表室，辽宁 大连 116001；3.中国人民解放军第七八一四工厂，辽宁 大连 116001)

0 引言

三体船具有良好的快速性和耐波性，在军事和民用领域具有广阔的发展前景。连接桥是三体船结构中最关键的一部分，该处在波浪力与船体惯性载荷的共同作用下存在着很大的应力，尤其是连接桥与主船体、舷侧连接处及转角处区域应力集中最为明显，而应力集中区域往往是疲劳问题的高发区域，会导致结构疲劳寿命降低。

对三体船来说，结构优化设计在减轻三体船结构重量的同时还能减小应力。徐敏等[1]对比了横骨架式、纵骨架式、密加筋式和箱型梁式这4种形式的连接桥结构应力特性，确定了较优的结构形式；杨赵华[2]以英国“海神”号三体试验舰为基础，对密加筋式、横骨架式和纵骨架式的连接桥进行了强度和砰击响应分析，得出了较优的轻量化结构；张聪等[3]应用变密度拓扑优化方法对三体船舱壁结构进行优化，实现了非水密舱壁结构的轻量化设计。针对三体船连接桥应力集中问题，周萍等[4]对比了不同材料连接桥的应力水平，并通过增加肘板改善了应力集中现象；张超[5]直接计算确认了三体船应力集中位置，针对连接桥进行优化设计并验证了方案的有效性；操安喜等[6]针对连接桥端部应力集中问题，提出“靴型”过渡的连接桥优化结构形式。

目前相关研究多基于整体式连接桥，模型多是英国“海神”号、美国的“独立”号等大型三体船。近几年，随着无人驾驶技术兴起，三体无人艇的研发成为了三体船发展新热点。通常50 m以下的三体无人艇，属于小型三体船。小型无人艇群的协同作战是美国军方无人系统体系的重要组成部分，其他国家也都有类似的发展战略和计划，可见，小型三体无人艇已经成为未来三体船发展的重点方向。黄立为[7]基于某小型三体无人艇提出了一种新型分布式连接桥结构，与传统整体式连接桥相比，结构重量和重心均大幅下降，但该结构只是提高了连接桥的抗弯能力，并未有效解决连接桥应力集中问题。

本文以某小型三体船为研究对象，利用有限元方法直接计算连接桥在多种工况下的结构强度，确定应力集中区域，探索不同半径的转角圆弧形状对连接桥应力集中现象的优化效果，并统计结构重量进行对比，其分析结果可为三体船连接桥结构设计提供参考。

1 三体船结构有限元分析

1.1 模型概述

某小型三体船主要参数见表1。

全船采用分布式连接桥，由2根箱型梁连接主船体与片体，布置见图1。

该船材料采用Q235普通船用钢，其屈服强度为235 MPa，对应的许用von-mises应力[σvm]=188 MPa，许用正应力[σ]=178.6 MPa，许用切应力[τ]=101.1 MPa。利用MSC Patran软件建立全船有限元分析模型，连接桥面板宽度为400 mm，腹板高度为250 mm。外板、连接桥、纵桁、强横梁、横舱壁、强肋骨等采用四边形板单元，普通横梁、普通肋骨采用梁单元。全船有限元模型见图2。

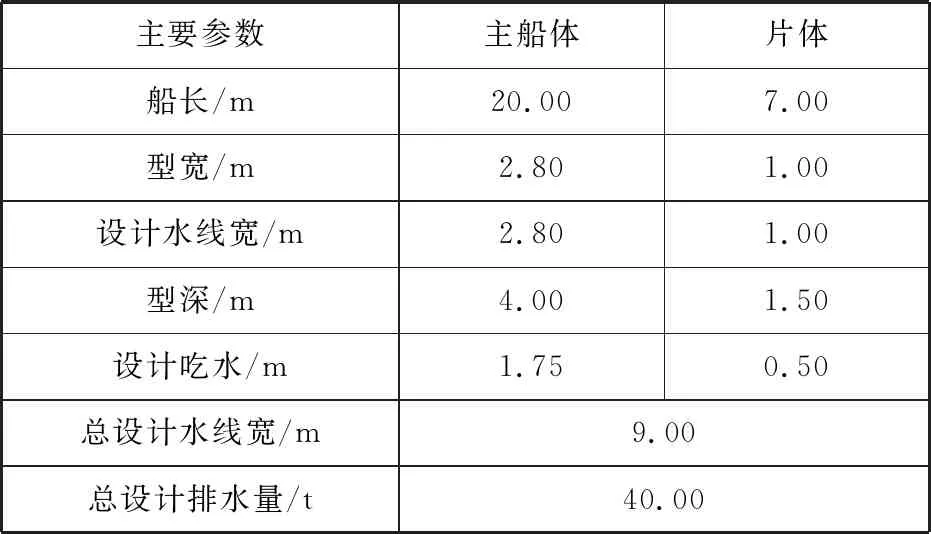
表1 三体船主要参数

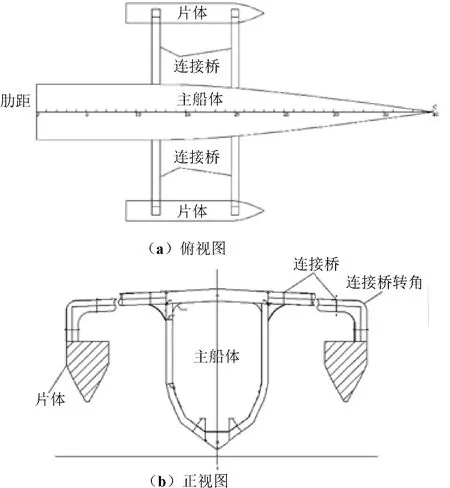
图1 三体船布置图

图2 全船有限元模型

1.2 工况选择

三体船所承受载荷包括总纵垂向弯矩、水平波浪弯矩、纵向扭矩以及其特有的横向分离弯矩和横向扭矩。采用《海上高速船入级与建造规范》中的计算公式来确定三体船的载荷，计算结果见表2。

船舶在实际航行时会受到各类载荷的同时作用。对三体船的强度直接计算分析，应当考虑船舶运动中存在的多种载荷耦合的情况。在确定各项单一载荷的基础上，可通过不同的组合工况来模拟实船的受力。本文参考劳氏船级社对三体船的规范要求，对7种典型工况进行计算，这些工况包含了迎浪、横浪和斜浪3种海况，每种工况中都有1种载荷达到最大值。这些工况中载荷成分见表3，表中“—”代表工况中不存在该载荷。表2中载荷计算结果与表3中对应的系数相乘作为该工况下的主要载荷。

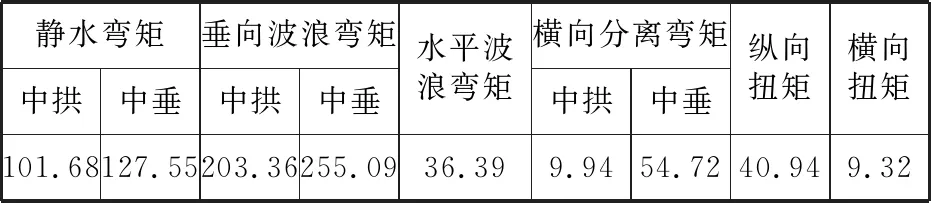
表2 三体船计算载荷 单位：kN·m

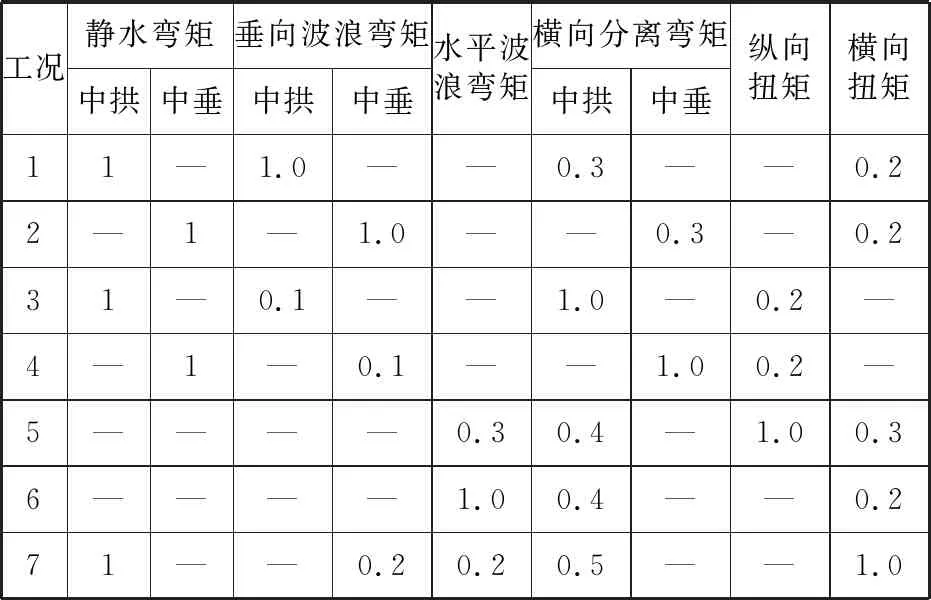
表3 各工况下的载荷成分

垂向波浪弯矩按中拱和中垂2种情况，换算为沿船长方向分布的一系列等效集中力，加载于船底纵桁；横向分离弯矩换算为等效的横向对开力，施加于片体龙骨；横向扭矩换算为侧体半船长上反对称分布的均布载荷等效施加于片体龙骨；水平弯矩和纵向扭矩换算为一系列力偶，施加于各强框架与舷侧相交位置。

1.3 边界条件

在中纵剖面上艏柱、艉封板水线处各取1点，约束垂向位移；在甲板、龙骨与中纵剖面相交处各取1点，约束纵向位移；在片体中横剖面龙骨处各取1点，约束横向位移。这种约束模式不仅能限制全船刚体运动，而且不影响船体各部分的相对变形。

1.4 强度计算结果

对全船进行有限元计算，各工况下连接桥与主船体、片体连接处及转角处的应力值见表4。从表4可见，工况4中连接桥转角处最大应力显著高于其他工况，高达136 MPa，已经接近许用应力，显示该处存在着较严重的应力集中问题。工况4的连接桥应力云图和转角处局部应力云图分别见图3～图4。由于连接桥转角是横向构件和垂向构件交汇的地方，存在结构型线的突变，该处应力较大，是应力集中的重点区域，因此有必要开展结构优化，让结构更平滑地过渡，以降低连接桥应力集中水平。

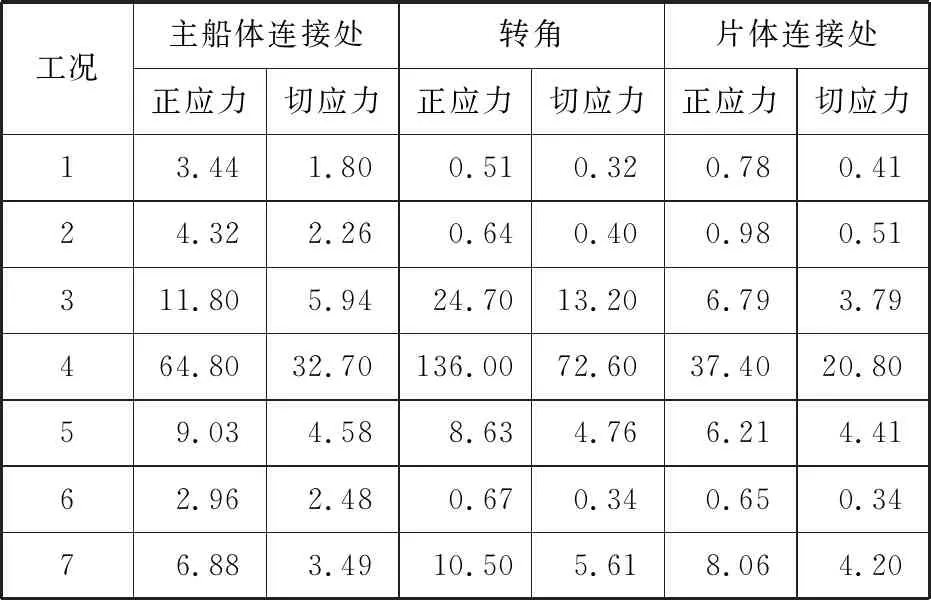
表4 各工况下的应力 单位：MPa

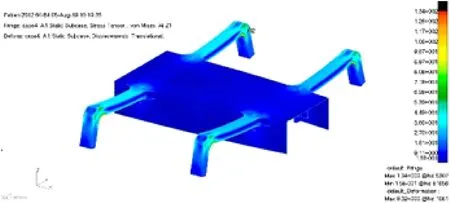
图3 连接桥应力云图

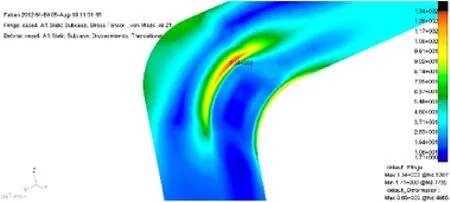
图4 局部应力云图

2 三体船连接桥转角优化分析

2.1 圆弧系列形状模型

原结构中，连接桥转角处采用圆弧过渡，圆弧半径为250 mm。为探索圆弧半径变化对连接桥应力水平的影响，步长按100 mm计算。此处建立了转角圆弧半径r从350 mm到950 mm的圆弧系列形状全船模型，并对其进行结构强度分析。半径为350 mm和950 mm的连接桥转角形状见图5。

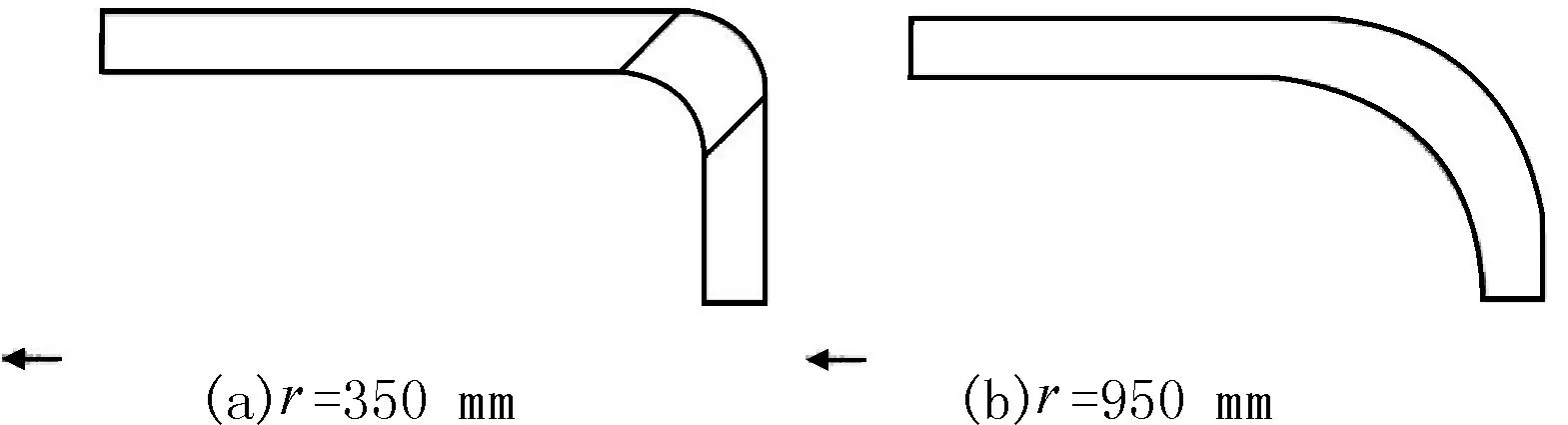
图5 不同半径的圆弧形状转角

2.2 计算结果及分析

加载方式和边界条件等设定与原模型相同。对该系列模型进行结构强度分析，本文仅对连接桥最危险的工况即工况4、连接桥转角以及舷侧连接处的最大应力进行分析，结果见表5。

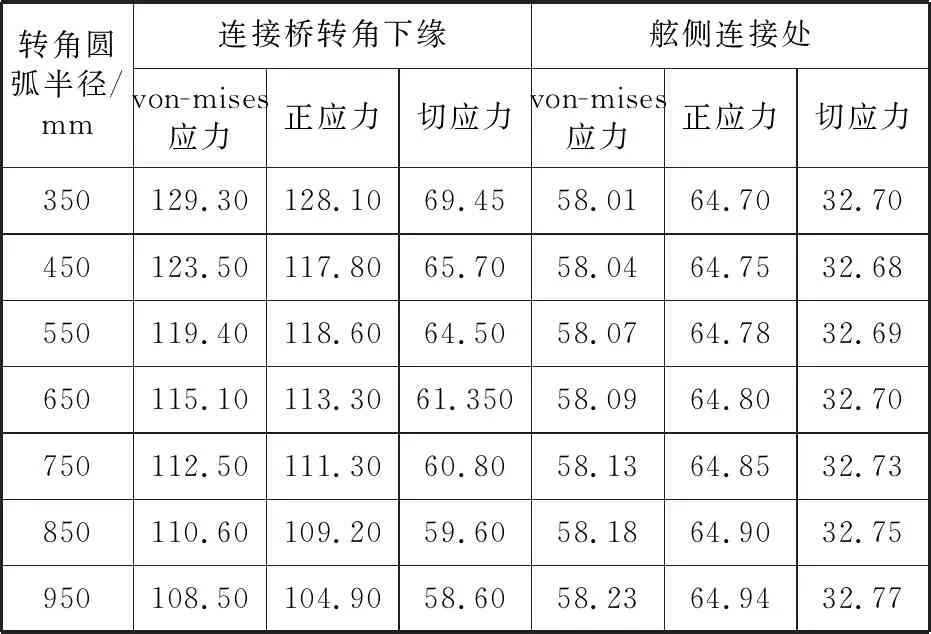
表5 工况4的应力 单位：MPa

从表中可以看到，在连接桥转角圆弧半径从350 mm增加到950 mm的过程中，连接桥与舷侧连接处的von-mises应力仅增加了0.22 MPa，几乎可以忽略不计。这是因为转角处形状的变化并未改变连接桥与舷侧连接处的局部结构，因此这种优化设计方法对舷侧连接处基本没有影响。随着圆弧半径增大，连接桥转角处的应力变化则明显得多。同时，转角处的von-mises应力从129.3 MPa下降到了108.5 MPa，下降百分比为16.09%；正应力从128.1 MPa下降到了104.9 MPa，下降百分比为18.11%；切应力从69.45 MPa下降到了58.60 MPa，下降百分比为15.62%。结果表明：连接桥转角半径的增加能够减小该处的最大应力，说明增加圆弧半径以减小局部应力集中的优化设计思路是可行的。

为具体说明转角圆弧半径变化与应力变化之间的关系，对工况4下3种应力随半径变化的关系进行了拟合，拟合结果见图6～图8。从图中可以看出，随着转角形状圆弧半径的增加，转角处的最大应力呈现出线性下降趋势。根据线性拟合的结果，转角形状圆弧半径每增加 100 mm，最大von-mises应力下降约3.4 MPa，最大正应力下降约3.6 MPa，最大切应力下降约1.7 MPa。

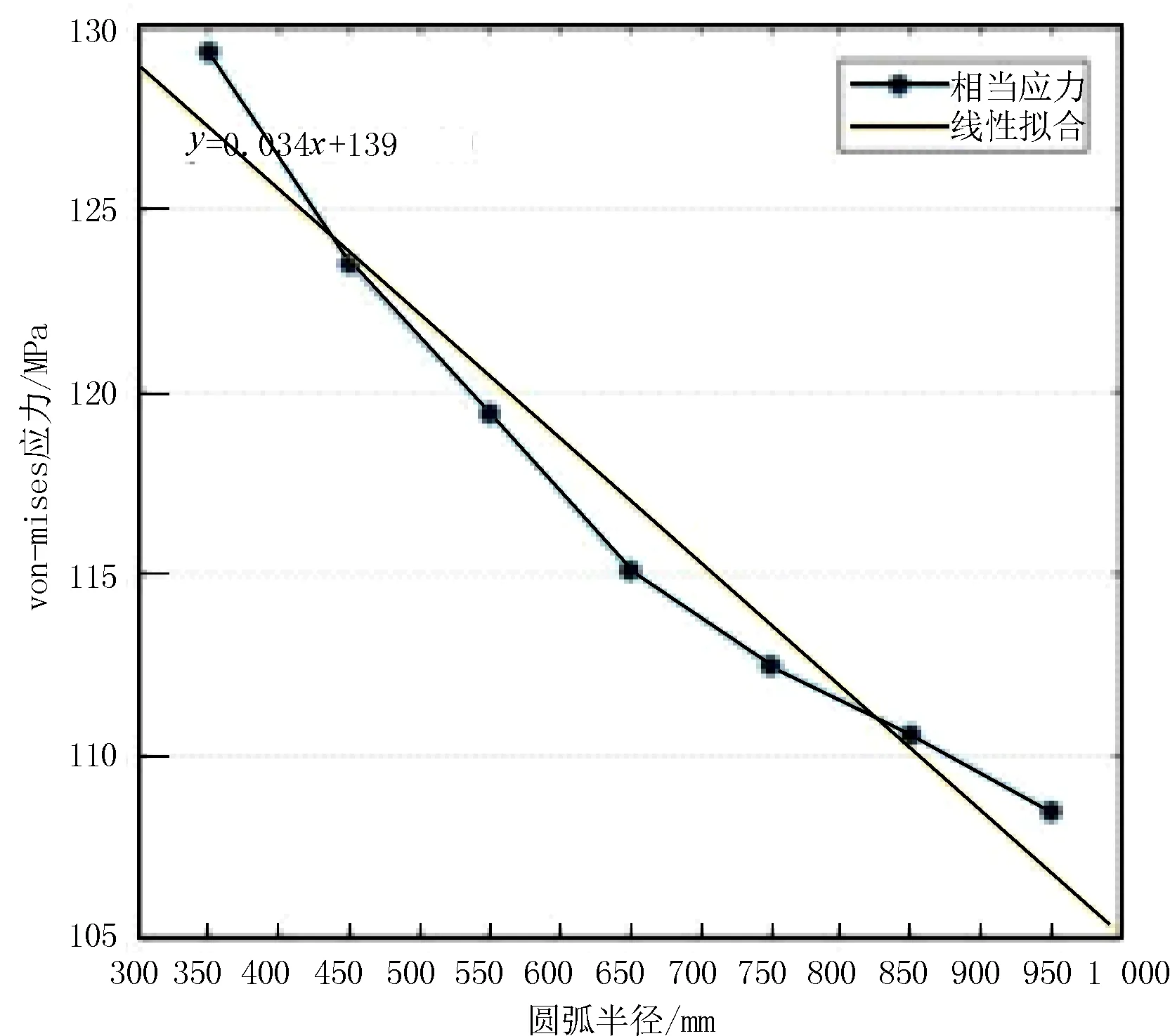
图6 von-mises应力与圆弧半径的关系

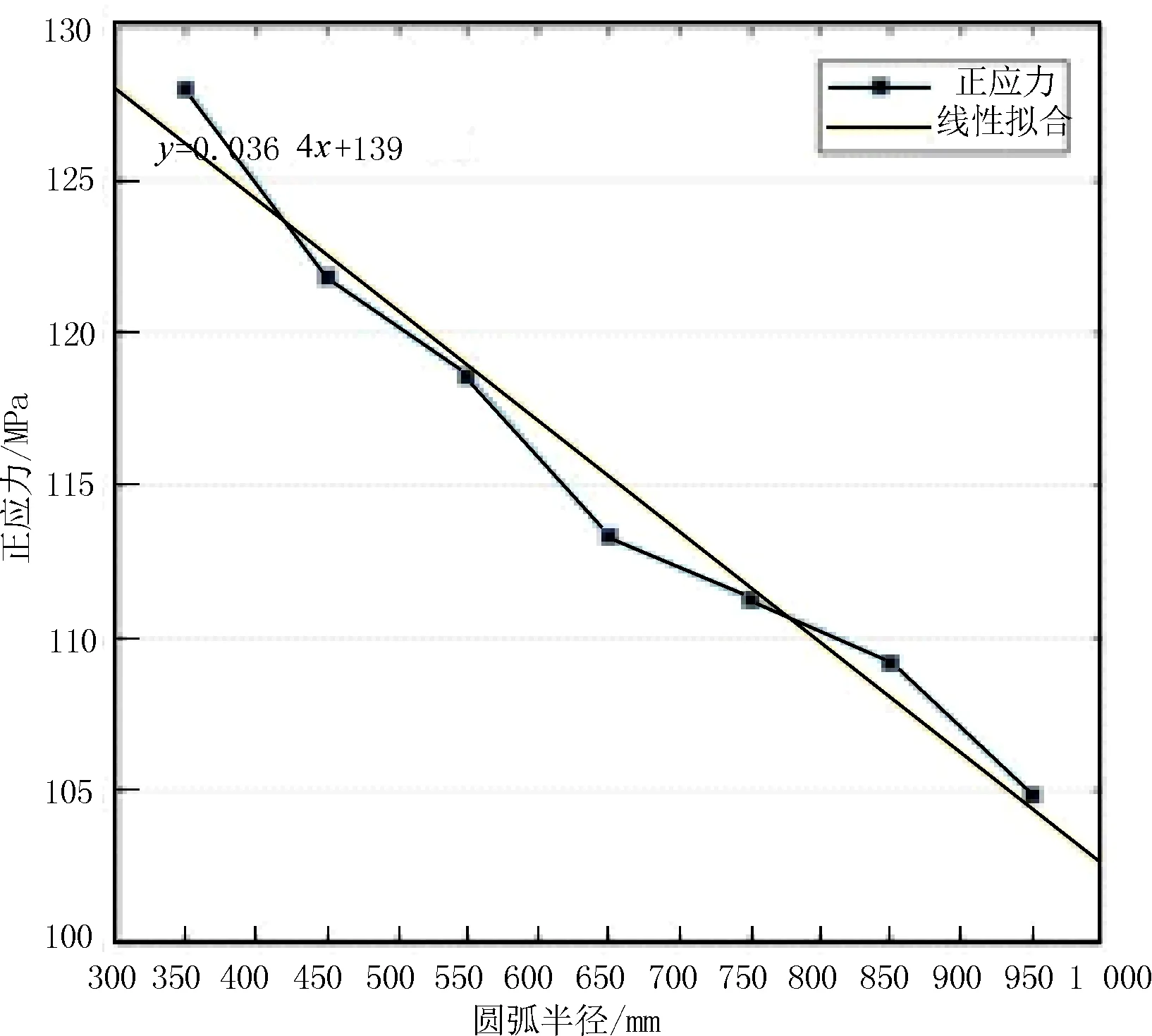
图7 正应力与圆弧半径的关系

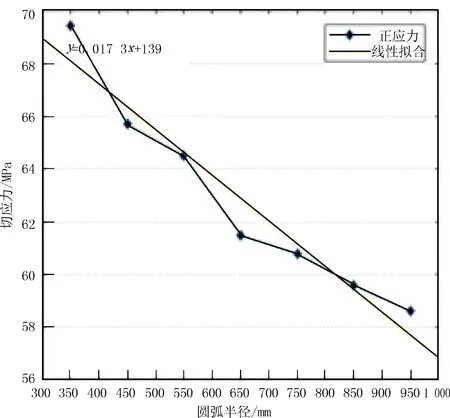
图8 切应力与圆弧半径的关系

为分析圆弧形状的减重效果，对该系列模型的连接桥结构质量做了统计，结果见表6。从表中可以看出，转角形状圆弧半径每增加100 mm，连接桥结构总重量降低64～66 N。

3 结论

本文基于有限元方法，计算了三体船在多工况下的应力分布，确定了连接桥应力集中区域，探索了连接桥转角过渡圆弧半径对结构应力水平的影响，有效减少了连接桥应力集中现象，降低了结构重量。通过数值计算和对比，可得出如下结论：

(1)圆弧形状能改善连接桥转角应力集中现象，减轻结构重量，是一种具有实用价值的连接桥设计方案。

(2)随着连接桥转角过渡圆弧半径增大，该处应力减小，结构重量降低，两者与圆弧半径近似成线性关系。

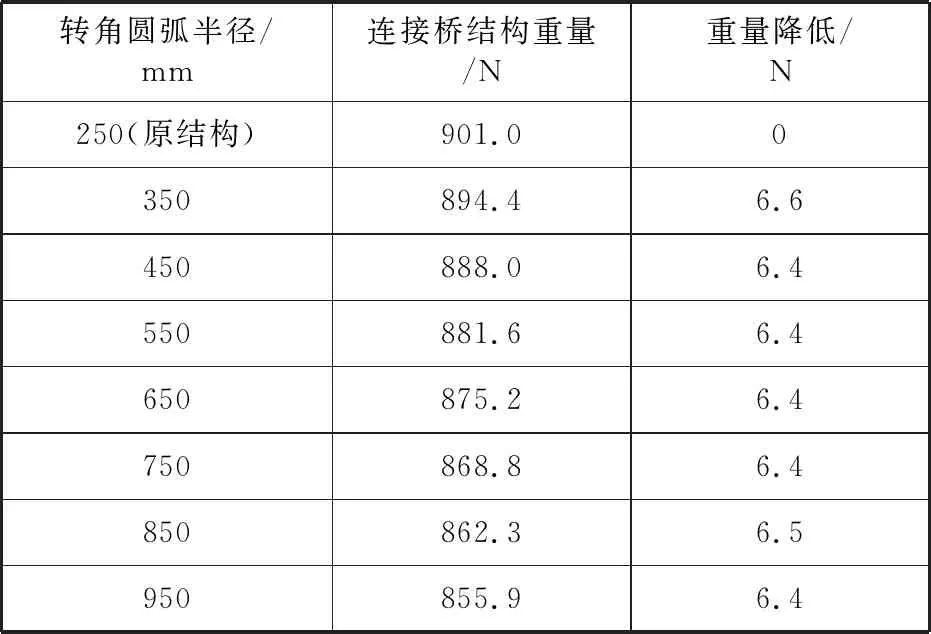
表6 连接桥结构重量