矿山巷道三维动态建模机制研究

王 彬，冀 虎，戴 锐

(矿冶科技集团有限公司，北京 100160)

矿山巷道是在矿体之间钻凿出的各种通路，用来运矿、通风、排水、行人以及为采出矿石新开凿的各种必要准备工程等，对生产安全和经济效益具有直接的影响。矿山的三维巷道模型是安全监测与预警分析的基础。传统矿山巷道是基于CAD并且以线段方式描述巷道，通过截面扫描生成三维巷道模型，其模型的精度无法控制。因此，如何动态生成满足数学模型精度要求的三维三角面片模型是一个值得深入研究的问题。

众多学者也对巷道的动态建模进行了大量研究。张进修、贾庆仁等研究了自动重建三维模型的方法[1-3]，但其数据源并非大多矿山采用的CAD线段，邹艳红等致力于解决一种断层面切割矿体三维模型的面-体布尔运算算法[4]，陶晓丽提出了通过3DMine软件构建三维矿山巷道[5]，李昀和谢景龙等均研究了动态构建三维模型的方法[6-7]，但未论述模型的精度如何控制。

本文通过CAD线段数据动态创建指定精度的三角面片实现巷道模型的三维建模。

1 巷道断面的三角面片建模机制

巷道断面分为半圆拱形、圆弧拱形、梯形、拱形等。本文以圆弧拱形巷道断面为例，阐述构建断面三角面片的过程。首先，将圆弧拱形巷道断面分成矩形与半圆两部分分别生成三角面片。

1.1 巷道断面B的三角面片建模机制

均分巷道断面B宽度W，使其分割后的巷道宽度W′小于或等于指定的误差精度δ。

均分巷道宽度计算公式：

(1)

依据同样的方法，均分巷道断面B高度H，使其分割后的巷道高度H′小于或等于指定的误差精度δ。

均分巷道高度计算公式：

(2)

均分巷道断面B后，生成2n×2m个四边形，将每个四边形的其中一对对角线相连，分成2个三角面片，最终三角面片的数量是2×2n×2m个。如图 1示例，假设误差精度为550 mm，宽度W被均分为8等份，高度H被均分为4等份，生成的三角面片数量为64个，效果如图 2所示。

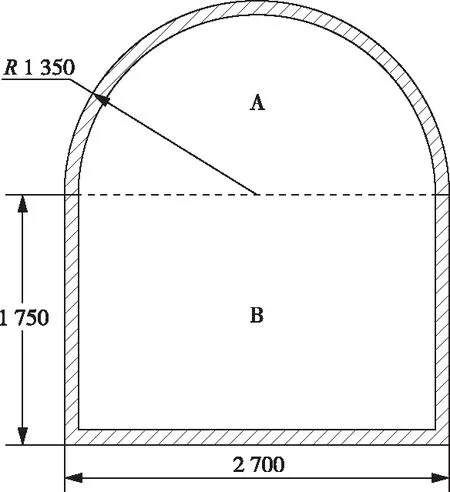
图1 圆弧拱形巷道断面(单位：mm)Fig.1 Cross section of arc arch roadway(Unit：mm)

图2 巷道断面B的三角面片建模效果(单位：mm)Fig.2 Modeling results of triangle patch of roadway section B(Unit：mm)

1.2 巷道断面A的三角面片建模机制

等角度均分半圆，使圆弧的弦长K′小于或等于指定的误差精度δ。

弦长的计算公式：

(3)

图3 巷道断面A的三角面片建模效果(单位：mm)Fig.3 Modeling results of triangle patch of roadway section A(Unit：mm)

2 巷道壁的三角面片建模机制

均分巷道壁深度L，使其分割后的巷道壁深度L′小于或等于指定的误差精度δ。

均分巷道宽度计算公式：

(4)

利用巷道断面A、B的计算方法，计算巷道断面每个均分点上与巷道壁的交点，将同一水平线的交点连接，形成多个四边形，每个四边形沿对角线分成两个三角面。最终完成对巷道壁的三角面片建模，其效果如图4所示。

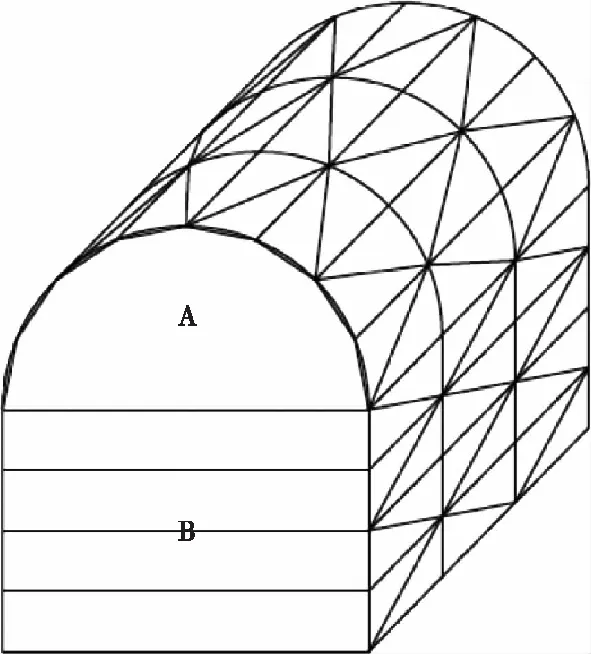
图4 巷道壁的三角面片建模效果Fig.4 Modeling results of triangle patch of tunnel wall

3 巷道底面的三角面片建模机制

以分割后的巷道断面B的宽度W′，分割巷道底面的宽度。以分割后的巷道壁的深度L′，分割巷道底面的深度。得到m个四边形，每个四边形沿对角线分成两个三角面。最终完成对巷道底面的三角面片建模，其效果如图 5所示。

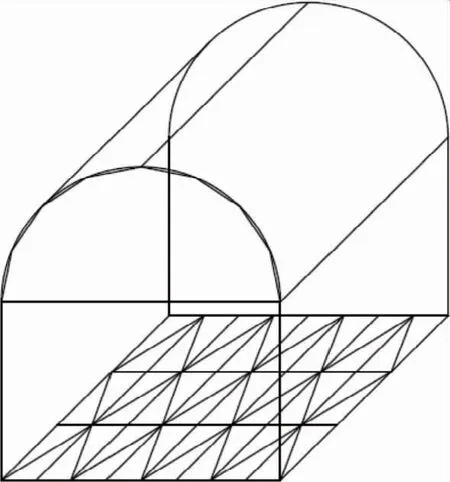
图5 巷道地面的三角面片建模效果Fig.5 Modeling results of triangle patch on roadway ground

4 巷道交点过渡模型的三角面片建模机制

在两个线段的交点处，会存在三角面片不连续或重叠的现象，如图6所示，需要做特殊的处理。方法是在交点处建立一个圆柱和一个半球，作为过渡模型，效果如图7所示。

图6 巷道端点不连续或重叠现象Fig.6 Discontinuity or overlap of tunnel end points

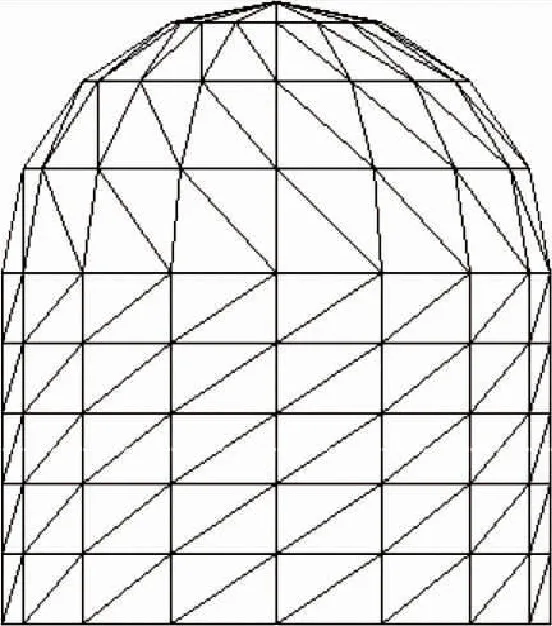
图7 巷道交点处的过渡模型Fig.7 Transition model at the intersection of roadway

4.1 圆柱的三角面片建模机制

圆柱的直径为巷道断面B的宽度W，高度为巷道断面B的高度H，将圆柱的上下顶面均分成n个扇弧，使其分割后的扇弧弦长小于或等于误差精度δ。计算公式见式(3)。将圆柱上下面的弦长顶点依次相连，便形成了正N棱柱。将正N棱柱的侧面高度H均分成m个四边形，使其均分后的高度H′小于或等于误差精度δ，计算公式见式(2)。将每个四边形对角线相连，分割成2个三角面片。最终圆柱侧面将被分成n×m×2个三角面片。效果如图8所示。

图8 圆柱侧面的三角面片建模Fig.8 Modeling of triangular patch on the side of a cylinder

圆柱的底面为正N边形，将正N边形的顶点与中点相连，形成n个扇面。将扇形以45°角度的方式分成8个三角面片，最终圆柱底面将被分成n×8个三角面片。效果如图9所示。

图9 圆柱底面的三角面片建模Fig.9 Triangular patch modeling of cylindrical bottom

4.2 半球的三角面片建模机制

半球的半径与圆柱的半径相同，将半球的经度也均分成n个扇弧，其均分的数量和点的坐标要与圆弧的上表面相同，否则构建的三角面片将不连续。将半球的纬度均分成n/2个扇弧。每两个相邻的经度与维度的交点连线，形成四边形。将每个四边形对角线相连，分割成2个三角面片。最终半球将被分成n×(n-1)个三角面片。效果如图 10所示。

图10 半球的三角面片建模Fig.10 Modeling of spherical triangles

5 融合模型

将预先建立巷道三角面片模型和巷道交点过渡模型逐一通过布尔并集运算融合成一个三角面片模型。最终的效果如图11所示。

图11 融合模型效果Fig.11 Fusion model effect

6 应用

应用本文的方法，针对新疆某矿450中段巷道，通过解析二维CAD线段数据，生成三维三角面片巷道模型，其三角面片数量为146 500个。在2019年9月份，使用微震传感器及微震数据采集软件共采集有效微震事件630个，应用微震数据处理软件将微震事件波形进行分析与处理，计算能量等微震数据。微震数据分析软件加载巷道模型和微震数据，首先计算各三角面片内心的三维坐标，利用插值算法计算各坐标点处的能量值，依据能量值，为三角面片附着不同的颜色，以可视化的方式呈现最终的效果，效果如图12、13所示。

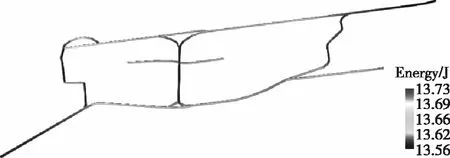
图12 450中段巷道的能量分布整体效果Fig.12 Overall results of energy distribution in 450 middle roadway

图13 450中段巷道的能量分布局部效果Fig.13 Partial results of energy distribution in 450 middle roadway

7 结论

应用本文中介绍的方法，能够生成指定精度的三维三角面片巷道模型。通过计算每个三角面片的内心三维坐标，依据相关数学模型的算法，计算地压、位移、应力等在这些坐标点的数值，并根据颜色卡，为每个三角面片填充不同的颜色。以三维可视化的方式，呈现地压分布、位移分布、应力场等。实验结果表明，应用该方法建立的三维三角面片模型，可以作为数学模型插值计算的有效依据，更易于对巷道的三维可视化分析，证明本方法具有实际的应用价值。