基于支持向量回归的油藏瞬态压力拟合

许恩华, 查文舒, 李道伦, 陈 刚

(合肥工业大学 数学学院,安徽 合肥 230601)

可靠的地质模型是油藏开发、管理的基础之一,也是可靠预测油井的保证。油藏建模无论是对工作人员知识和经验的要求,还是对资料的要求都很高;且建模工程不确定因素多、情况复杂,使得地质模型与油藏真实情况之间存在巨大差异。因此，需要使用已有资料对地质模型进行修正,尤其是包括了基于生产响应的地质信息的动态资料,这对于全面、准确评价地质模型非常重要。评价地质模型与真实油藏之间的差异是对比动态数据与地质模型计算的结果,即历史拟合。动态历史拟合方法是目前普遍采取的方式。

油藏工程中的历史拟合是一个典型的反问题[1]。与利用已知模型直接推断结果的正问题不同,反问题是利用已知结果反向推断模型参数再进行预测。由于不同参数值会得到同样的好的拟合结果,历史拟合的过程中会出现不适定性。

获得多个可靠模型且准确预测油藏情况是油藏工程和油藏数值模拟技术不可缺少的一部分,自动历史拟合作为其中的关键环节,其问题复杂、工程量和计算量巨大,一直是该领域内的研究热点[2-4]。

早期的传统历史拟合是人工调节参数,即油藏工程师凭借自身的经验手动不断地调整1个或者几个参数值，并对产生的模拟计算值与实际观测值之间的误差进行分析,从而达到最小误差,又被称为人工历史拟合。人工历史拟合不仅效率低,而且难以保证结果的准确性,并且无法满足油田开采发展提出的海量参数的需求。

在油田需求增加、计算机和数学工具发展的背景下,自动拟合技术得到迅速发展[5-6]。自动历史拟合是利用计算机、优化算法和拟合算法自动地调整油藏工程模型参数,使得模拟模型与真实油藏模型之间的差异在可接受的范围内。从最初基于线性回归的多项式拟合和优化算法结合的拟合技术[7]发展到基于贝叶斯方法[8]、响应面方法[9]、卡尔曼滤波方法[10]的自动历史拟合方法，自动历史拟合技术利用计算机解决了传统历史拟合方法中无法解决的问题。横向比较自动历史拟合中采用的各种方法,在收敛速度、精确性、非线性拟合、多参数拟合方面各有优劣。

响应面方法由数学方法和统计方法结合而成,可以对多个变量影响下生产响应的问题进行建模和分析,并得到体现生产响应与变量之间关系的显示表达式。20世纪90年代,响应面法被引入油藏工程,通过构造响应面模型并定义反映模拟计算值与实测值之间偏差的目标函数,响应面方法显著提升了地质模型的准确性。

贝叶斯方法起源于英国学者贝叶斯提出的贝叶斯公式和由其发展出的归纳推理方法,基本思想是利用贝叶斯公式将已知的概率密度参数和先验概率转换成后验概率,据此进行决策分类。在地质模拟和历史拟合的应用过程中,贝叶斯方法在模型推断、在线预测方面有显著的优势[8]。相比于传统统计推断方法,贝叶斯方法能利用计算机处理更大的数据集。先验信息的收集是贝叶斯方法中的重要部分。

卡尔曼滤波方法是一种基于统计和蒙特卡洛方法生成集合的平均梯度类方法,其中最广泛采用的是集合卡尔曼滤波方法。卡尔曼滤波方法的引入为描述油藏情况及动态预测中评价不确定性提供了一种新的方法。卡尔曼滤波方法具有计算效率高、鲁棒性强的特点,在吸收动态数据方面能做到持续、及时、迅速,有效减少计算时间,非常适合大规模非线性实时动态油藏模型更新的历史拟合,在计算机多核进行并行计算的条件下,能相互独立计算多个油藏模型并进行生产预测。模型更新的过程中,完全独立于所使用的模型方程,不需要对不同的油藏模拟器进行复杂的敏感计算,无需关注过程,在程序的开发、调试、维护方面有非常大的优势。

支持向量机(support vector machines,SVM)是一种基于结构风险最小化原则(risk minimization inductive principle)寻找集合中最优元素的机器学习算法。结构风险最小化涉及到同时最小化经验风险和VC维数。SVM主要有支持向量分类机(support vector classifier,SVC)和支持向量回归机(support vector regression,SVR) 2种。SVR在1997年被提出,与传统统计学中依据于所有训练数据与预测数据之间最小偏离的回归方法不同,支持向量回归依据的是所有数据最小误差界,因此支持向量回归只需要训练数据中的一部分子集即可,计算效率有了巨大提升的同时还保证了准确性。经过多年的发展,支持向量回归在字体和物体识别、回归和时间序列预测等方面取得了显著的效果。

可靠的地质模型是解决石油开采工程问题、进行产量预测的关键。试井分析是以测量井的井底压力、温度、流量等数据及其随时间的变化并结合拟合方法分析地层和井筒参数的方法,其为油藏工程开发提供准确的地层数据,为油藏动态特性和各种生产方式下的生产变化趋势提供可靠依据。经过多年的发展,该方法已经成为重要的油藏描述工具。

数值试井是近些年发展起来的一项试井解释技术[11-14],不同于基于渗流方程解析解的解析试井,数值试井是通过大量数值模拟来精确描述物理过程,应用场景更广。作为一项新技术,数值试井存在计算参数多、计算时间长、需要手动调节不确定参数等困难。解释一口井花费的时间跨度在几周到几个月之间,需花费大量的时间和人工成本,而自动调节不确定参数的方法可以大大减少人员工作强度。

现有的自动反演方法适用范围有限。响应面方法在多变量情况下的处理效果不好;集合卡尔曼滤波方法的计算量大、计算时间长。为此,本文基于支持向量回归,提出支持向量回归的自动反求参数的试井分析方法和利用多组数据衡量拟合效果的整体误差,并对试井数据进行模拟、验证。

1 理论背景

1.1 试井分析评价的目标函数

在单井试井分析中,需要通过“试凑”一组合适的“地层参数和井筒参数”使得渗流方程的计算压力逼近实测压力,这显然是一个反问题。一般采用目标函数OF反映随时间变化的计算压力、压力导数与井底实测压力之间的偏差,通常采用一个简单的平方和,即

其中,p为压力;f为压力降落;d为压力导数;i、j、k分别为压力、压力降落、压力导数的时间点序号;l、m、n分别为实测数据时间点的总数据;obs、sim代表实测数据值和模拟值;x为不确定参数;ω为权重。

在油气工程和试井分析的发展过程中,逐渐发现仅仅靠1组观测值是不能衡量模型误差,多组观测值能更加有效衡量模型误差,因此提出基于所有测量值的误差函数,即

其中,α为观测值组数;τ为观测值序号。

1.2 SVM和支持向量回归

假设训练数据集是{(x1,y1),…,(xl,yl)}⊂A×R,A代表数据点的模式。ε-SVR的目的是寻找f(x),使得尽可能多的数据点(xi,yi)包含在ε边界内。线性函数f(x)定义为:

f(x)=〈ω,x〉+b,ω∈A,b∈R

(1)

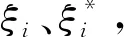
服从

(2)

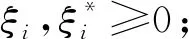
(3)

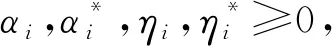
(4)

(5)

(6)

将(4)～(6)式代入对偶问题(3)式可得:

服从

(5)式可写为:

(7)

并且有:

(8)

这就是支持向量扩张,即ω可被xi线性表示,因此求f(x)时不需计算ω。由KKT条件求解得到b的求解式为:

b=yi-〈ω,xi〉-ε,αi∈(0,C)

(9)

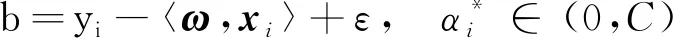
(10)

通过同样的推导方法可以得到引入核函数的ω表达式为:

(11)

分割函数f(x)的表达式为:

f(x)=sgn(〈ω,x〉+b)=

(12)

常用的核函数如下:

(1) 多项式核函数,即

k(μi,μj)=(μi·μjd)。

(2) 非匀次多项式核函数,即

k(μi,μj)=(μi·μj+1)d。

(3) 高斯核函数,即

k(μi,μj)=exp(-γ‖μi-μj‖2),γ>0,

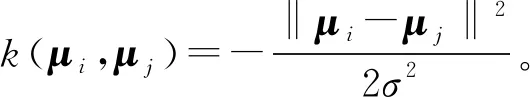
(4) 双曲正切核函数,即

k(μi,μj)=tanh(kμi·μj+c),

有时k>0,c<0。

1.3 BFGS算法

BFGS算法是一种梯度类优化算法,用于搜索函数的极值点。

由牛顿法和拟牛顿条件可知:

(13)

yk=Hk+1sk

(14)

其中,Hk为海森矩阵;gk为函数f(x)在xk处的梯度;sk=xk+1-xk;yk=gk+1-gk。

BFGS算法的基本思想是构造一个矩阵直接逼近海森矩阵,即Bk≈Hk。设迭代格式为:

Bk+1=Bk+ΔBk,k=0,1,2,…

(15)

其中,B0常取为单位矩阵。通过待定系数法可以求得Bk的迭代公式为:

(16)

下面给出BFGS算法的一个完整描述。

(1) 给定初值x0和精度阈值ε,并令B0=I,k∶=0。

(3) 利用线性搜索方法得到步长αk,令sk=αkpk,xk+1∶=xk+sk。

(4) 若‖gk+1‖<ε,则算法结束。

(5) 计算yk=gk+1-gk。

(7) 令k∶=k+1,转至步骤(2)。

(17)

进一步展开可得到:

(18)

1.4 方法与流程

(1) 确定试井拟合所用不确定参数及取值范围。

(2) 利用抽样算法抽取若干组试算算例。

(3) 将每组算例放入试井软件中进行计算,获得压力、压力变化、压力导数等数据。

(4) 使用基于不同核函数的支持向量回归模型对数据进行拟合,得到回归表达式和整体误差。

(5) 通过整体误差判断最优的支持向量回归模型,并作为试井分析所用模型。

(6) 定义试井分析评价的目标函数,并利用BFGS算法对其进行优化,求得最优的不确定参数值。

(7) 试井软件计算(6)式中所求的参数值组,求得压力值等数据,并与真实压力值对比;若满足误差,则计算结束,否则返回步骤(1)。

2 模型描述与案例研究

五点井网两相模型如图1所示。

图1 油藏形状及井分布

油藏大小为600 m×400 m×10 m,厚度为10 m,孔隙度为0.2。图1中，井1为生产井；井2、井3、井4、井5为注入井；井1、井2、井3周边存在径向复合区域,所有井都开井80 d,然后关井2 d。生产井生产流量为40 m3/d,注入井注入流量均为10 m3/d。

采用PEBI网格划分技术,网格如图2所示。其中，实验平台是Interl®CoreTMi7-7 700 K CPU@4.20 GHz,实验环境是64位Windows7操作系统。

图2 油藏网格划分

本文方法选定的9个不确定性参数为:地层渗透率K,范围为(100 mD,1 000 mD);5个区域渗透率K1、K2、K3、K4、K5,范围为(100 mD,1 000 mD);生产井和注入井表皮因子S1、S2、S3,范围为(-1,3)。本文的研究在注采平衡的前提下进行,拟合对象是压力恢复段生产井压力曲线、压力变化和压力导数双对数曲线。

利用抽样算法随机抽取2 000组试算算例,所有算例都满足渗流方程。将所有算例放入数值试井模拟器中计算压力值等数据。2 000组试算算例中的前500组被假设为观测值,其余1 500组用来构造支持向量回归模型并定义整体误差,不同模型的整体误差见表1所列。

表1 模型整体误差

比较整体误差后,选取三次支持向量回归模型(Cubic)作为试井分析所使用的拟合模型。随机选取初始点,使用BFGS算法进行优化，得到不确定参数的估算值,误差判断标准是使目标函数OF尽可能小。将2 000组数据的第1组作为真实值,由此得到估算值和真实值所对应的压力恢复段的井底压力的对比、压力变化及压力导数的对比,如图3所示。

拟合不同核函数支持向量回归模型的耗时见表2所列。由表2可知,使用BFGS算法进行优化耗时为90.488 132 s。可见支持向量回归模型可以准确确定试井分析所应采用的拟合模型,并能准确反演正确的地层参数及井筒参数。

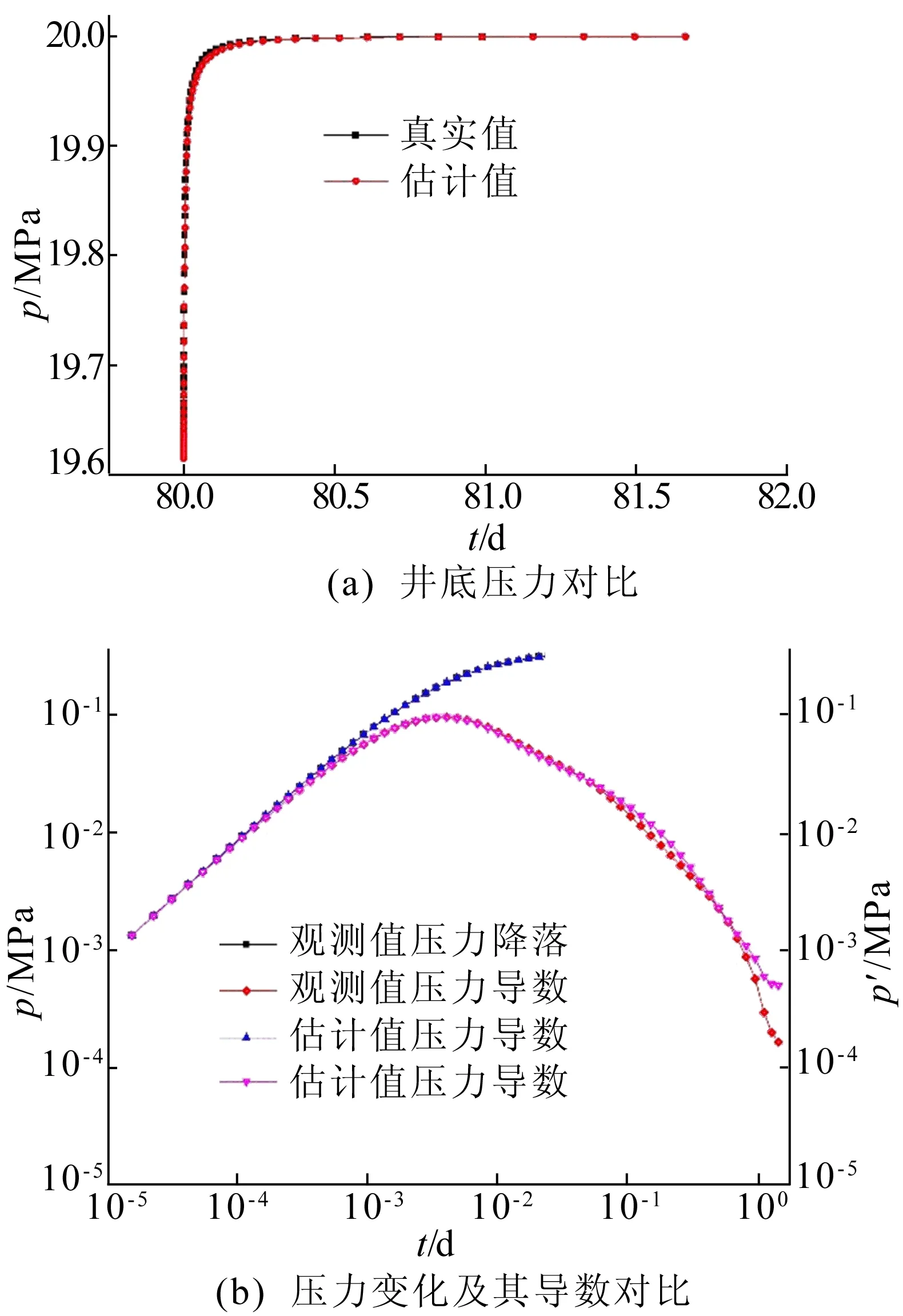
图3 基于支持向量回归方法的自动拟合结果对比

表2 拟合支持向量回归模型耗时

3 结 论

本文提出了基于支持向量回归和BFGS优化算法的试井自动反演方法,主要结论如下:

(1) 基于实测的井底压力、压力降落、压力导数,支持向量回归拟合方法和BFGS优化方法能有效地进行地层参数反演。

(2) 通过对比不同核函数下的支持向量回归模型误差发现，三次支持向量回归模型最适宜估计试井分析模型。

(3) 本文提出的试井自动反演方法能大大提高现场人员的工作效率,具有很好的应用前景。

另外,本文方法还有待于深入研究,例如方法的稳定性以及抽样方法、优化方法等对反演结果的影响。