风电系统有功环流严重度概率评估
李生虎, 薛 婧, 张晓艳, 赵慧洁, 胡 涛
(合肥工业大学 电气与自动化工程学院,安徽 合肥 230009)
0 引 言
电力系统有功环流,将增加输电损耗、影响继电保护动作特性、降低线路输电能力、甚至引起过载或停电事故[1-2]。电网拓扑结构或潮流控制器参数不合理,都可能引发环流[3-4]。目前我国特高压及超高压电网处于建设初期,网架结构较为薄弱,为获取最大网络传输功率并合理利用资源,部分地区电磁环网采取合环运行方式,增加了环流风险[5]。
文献[6]根据潮流分布检测环流存在路径,采用最优潮流寻找设备最优设定值以消除环流。为衡量环流严重程度,可以使用环流回路中有功网损大小作为判断依据,当网损最小时环流消失[6-7];也可以根据环流回路中传输功率的大小及方向量化环流[8-9]。但是,上述研究的前提是电网结构简单或结构复杂但环流路径固定。若由于设备参数调整、出力波动等原因,导致环流路径发生改变,对不同环流路径中的循环功率或有功网损进行对比,则缺乏实际意义。
在现有环流研究中,对系统中不确定因素影响考虑较少。随着风电并网容量快速增加,风电随机变化改变电网潮流分布[10],基于特定场景的环流分析结果存在误差。文献[11]考虑了风电场出力和统一潮流控制器(unified power flow controller, UPFC)设定值对环流的共同作用,利用区间数表示风电出力波动范围,建立区间潮流模型。但是该模型仅用于确定不会造成环流的UPFC设定值范围,并未说明超过该范围时环流严重程度。
对于电网规划及运行调度,需要对所有场景中有功环流进行概率评估,还需要定义环流严重程度,以综合评估不同场景下环流严重程度。马尔科夫链基于历史数据,建立随机序列时序模型,已运用于设备检修决策、系统可靠性评估等领域[12-15]。若考虑环流特性对马尔科夫链模型进行改进,则可能预测不同环流状态的发生概率。
针对风电并网后电力系统有功环流问题,本文建立基于马尔科夫链的有功环流多状态模型,根据有功环流数量划分环流状态,通过风速历史数据建立状态转移概率矩阵,结合初始状态可快速预测未来时刻不同环流状态发生概率。寻找环流具体路径并定义环流支路占比,该比值反映了环流规模大小,可量化环流严重程度。结合环流概率及严重程度,定义有功环流严重度指标,计算不同时刻指标值以预估环流风险。调整移相器角度构建不同电力系统场景,计算平稳状态严重度指标并进行对比,得出相应结论。以新英格兰39节点系统为例,验证了所提算法的有效性。
1 随机风电功率建模
为充分考虑不同风速对有功环流影响,采用K均值聚类算法对风速进行聚类,并对分类结果进行显著性水平检验,以保证分类有效性[10]。然后将风速数据转化为风电场出力。
1.1 K均值聚类算法处理风速数据
取L个时间断面的风速样本cb,b=1,2,…,L。将其聚类为K类,记第h类样本类别为Zh,样本集合为Hh,所含样本数为lh,h=1,2,…,K。取类均值vh为第h类类中心,即
(1)
定义样本cb与第h类间距离,为该样本与类均值间欧式距离。首先等步长分类,然后根据总误差最小原则将风速样本划分到与其距离最近类中去,直到总误差ERΣ不再减小为止。ERΣ计算公式为:
(2)
1.2 分类效果检验
借助Wilks统计量进行显著性检验,判断分类是否明显。根据样本数据构建类内离差值wa和类间离差值wb,总离差值wt=wa+wb,其中
(3)
(4)
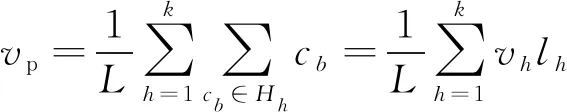
(5)
类内离散度越小、类间离散度越大时,分类效果越好。
定义统计量wu=wa/wt,则有:
-[(L-1)-(1+K)/2]lnwu~χ2(K-1)
(6)
若(6)式大于卡方分布临界值,则认为分类有效;否则,需要减少分类数,重新分类。
1.3 风电场出力计算
根据风速样本聚类结果,结合风电机组有功出力特性(7)式,即可得到风电机组有功概率分布。
(7)
其中,PW、Pra分别为风电机组有功出力及其额定值;vci、vra、vco分别为切入风速、额定风速、切出风速。
风电机组无功出力,可以选择恒功率因数(cosφ)、无功为定值或考虑电压下垂特性设置无功出力。
2 有功环流判断方法
采用Floyd-Warshall算法[11],通过迭代寻找所有节点间最短路径,确定有功环流具体路径及环流数量。算法具体步骤如下:
(1) 定义初始距离/路径矩阵。将支路有功流向设为支路方向。当x、y为不同节点,节点间存在支路且方向为x至y,则记为x→y,否则x~y。若系统有a个节点,定义初始距离矩阵R=[rxy]a×a及初始路径矩阵U=[uxy]a×a元素如下:
(8)
(9)
其中,Yxy为支路导纳。
(2) 更新距离矩阵/路径矩阵。迭代寻找更短路径,即对于每个距离矩阵元素rxy(x≠y),判断是否存在中间节点o,使得rxo+roy (3) 根据最终路径矩阵,判断环流路径。选取任意非无穷大元素uxy,首先判断行数x至其列数y通路路径:若uxy=x,则该路径为最短路径,否则更新路径为x→uxy→y;继续拓展x→uxy及uxy→y直至每相邻两节点都是最短路径。然后判断列数y至行数x通路路径,合并得到最终环流路径。 考虑随机风电并网,选取某个环流特性划分系统有功环流状态,并量化该状态环流严重程度。将各环流状态出现概率与其严重程度相乘,相加得到系统有功环流严重度指标,定义如下: (10) 为计算有功环流严重度指标,基于历史数据建立有功环流多状态模型,估计未来时刻环流状态发生概率。 马尔科夫链是具备“无记忆性”的随机过程,即对于时刻点0≤t1 FX(tn)|X(tn-1)=FX(tn)|X(t1)…X(tn-1) (11) 假设马尔科夫链是时齐的,即在状态空间E={e1,e2,…,em}中,满足: p[X(t+Δt)=ej|X(t)=ei]= p[X(Δt)=ej|X(0)=ei]=pij(Δt) (12) 其中,pij(Δt)为时间间隔Δt内状态ei和状态ej之间的转移概率,i,j=1,2,…,m。 有功环流状态划分越细,越为精确,但是计算量越大。折衷准确性和计算量,以下将环流存在状态划分为m=3,即正常状态、单环流状态以及多环流状态,定义如下: (1) 正常状态H。电力系统运行合理,没有产生有功环流; (2) 单环流状态S。出现单条路径有功环流,环流经过支路较少,但仍会加重线路负载、增加系统网损; (3) 多环流状态M。有功环流路径增多,环流严重程度加剧,对系统危害加重,甚至可能影响系统安全。 根据上述划分方法,将系统有功环流状态空间记为E={eH,eS,eM},状态转移概率矩阵如下: (13) 当系统样本数量足够多时,根据相邻时刻的状态转移情况可获得满足一定误差要求的状态转移概率矩阵p。 理想情况下,当样本数量趋近于无穷大时,p的统计值无限接近于真实值。 定义向量Π(d)为td时刻有功环流状态分布,即 (14) 假设电力系统初始运行状态为Π(0),根据状态转移概率矩阵定义,经过Δt时间后,有功环流状态分布为: Π(1)=Π(0)p (15) 于是经过q个Δt时间后,有功环流状态分布为: Π(q)=Π(q-1)p=Π(0)pq (16) 若已知电力系统初始有功环流状态和状态转移概率矩阵p,则可快速获得电力系统未来某时刻有功环流概率分布情况,即pF(eH)、pF(eS)及pF(eM)。 平稳状态概率表示经过足够长的时间后,系统状态分布趋于恒定,与初始状态无关。平稳状态概率满足: Π(∞)=Π(∞)p (17) 由于(17)式中只有m-1个式子独立,联立可求解平稳状态概率,即 πH(∞)+πS(∞)+πM(∞)=1 (18) 根据Floyd-Warshall算法,不同有功环流经过环流路径不同,则可定义环流支路占比,量化环流严重程度。 环流支路占比定义如下:若出现环流,环流路径包含支路数占系统总支路数的比值,表征了环流规模大小,可反映环流严重程度,将其定义为sev(ect),ct=1,2,3。 (19) 其中,KH、KS、KM分别为属于H、S、M的风速类别数,满足KH+KS+KM=K;Nch、Ncs、Ncm分别为该风速类别下环流路径所占支路数;Nsys为系统总支路数。 正常状态H下,由于不存在有功环流,Nch=0,则sev(eH)=0;单环流状态S以及多环流状态M满足0 综上所述,系统严重度指标满足0≤Isev≤1。Isev=0意味着即使考虑风电波动,系统始终不存在有功环流。Isev越接近于1,代表系统有功环流风险越高,有功环流后果可能越严重。 考虑电力系统运行方式变化及不确定性,有功环流处于动态变化之中,严重度指标在不同时刻数值不同。而根据系统平稳状态有功环流概率得到的平稳状态严重度指标是固定值,可用于快速比较电网设计或运行调度方案的合理性。不失一般性,以双芯对称离散型可控移相器(TCSD-TCPST)为例[12,16],构建不同运行场景,对有功环流严重度进行概率评估,如图1所示。 图1 有功环流严重度概率评估 以新英格兰39节点系统为例,检验所提算法,系统环流路径如图2所示。在节点21接入风电,装机容量500 MW,cosφ=0.95。取vci=4 m/s,vra=14 m/s,vco=25 m/s。TCSD-TCPST位于支路4-14始端,增加节点40。系统基准容量取100 MV·A。 图2 新英格兰39节点系统环流路径 选取某地区一年内每5 min共105 120个风速样本,进行K均值聚类,分类数设定为K=20。每次迭代各样本类别调整样本个数、类均值vh(m/s)及包含样本数lh,见表1所列。对聚类结果进行显著性水平检验,统计量wu=0.009 9,(6)式计算结果远大于卡方分布临界值,证明了分类有效。 表1 风速样本聚类迭代过程 本算例调整移相器角度构建不同电力系统场景,首先假设移相器处于组态T=-6,即移相角α=-11.96°,计算严重度指标。 在所有风速类别下,计算风电机组出力,并根据系统潮流分布进行环流判断。若存在环流,则提取最终路径矩阵U中的非零元素得到矩阵UNZ以判断环流路径。计算结果如下:风速类别Z1,Z2,…,Z6下系统不存在有功环流;Z7、Z8下系统存在有功环流;Z9,Z10,…,Z20下系统存在有功环流。不同风速类别下环流路径矩阵如图3所示。 图3 不同风速类别下环流路径矩阵 由UNZ1判断环流路径C1:4→40→14→13→12→11→6→5→4;在C1的基础上增加了C2和C3,由UNZ2判断环流路径,其中C2:4→40→14→13→10→11→6→5→4;C3由C1和C2叠加而成:10→11→6→5→4→40→14→13→12→11→6→5→4→40→14→13→10。将系统中环流流经支路简化(图2),支路有功流向及C1、C2路径在图中已标出。 综上可得,若某风速样本属于风速类别Z1,Z2,…,Z6,此时系统处于正常状态H;若属于风速类别Z7、Z8,则系统处于单环流状态S;若属于风速类别Z9,Z10,…,Z20,系统处于多环流状态M。 根据环流路径,计算环流严重程度sev(ect)。所取系统Nsys=47,可以得到: (1) 正常状态H。KH=5,Nch=0,ch=1,2,…,5。sev(eH)=0。 为计算状态转移概率矩阵,统计上述风速样本下系统有功环流状态及其转移情况,见表2所列。 由表2可知,系统处于正常状态H的概率为40.42%,处于单环流状态S的概率为27.08%,处于多环流状态M的概率为32.50%。 表2 环流状态转移数据 根据表2,计算得到系统有功环流状态转移概率矩阵,即 状态转移概率矩阵的意义为:假设系统有功环流处于状态H,则在下一时刻有0.927 4的概率保持在状态H;有0.070 8的概率转移至状态S;有0.001 8的概率转移至状态M。 可以看出,状态转移概率矩阵对角线元素值明显大于两侧的元素值,具有传统转移概率矩阵“山脊”特性,系统以较大概率保持上一时刻有功环流状态。 假设系统初始状态为正常状态,即Π(0)=[1,0,0]。记经过q个Δt时间间隔后严重度指标为Isev(q),则此时严重度指标Isev(0)=0。 根据(15)式,经过矩阵乘法运算,Δt时间间隔后有功环流概率分布为Π(1)=[0.927 4,0.070 8,0.001 8],即pF(eH)=0.927 4,pF(eS)=0.070 8,pF(eM)=0.001 8。则可得到Δt时间间隔后严重度指标Isev(1)=0.012 4。同理可快速获得任意时间间隔后的严重度指标。 结合(17)式、(18)式可以得到系统平稳状态有功环流概率分布:Π(∞)=[0.404 2,0.270 8,0.325 0],平稳状态严重度指标Isev(∞)=0.115 3。 系统处于不同初始状态的严重度指标变化过程如图4所示。由图4可知,初始状态为多环流状态M时,指标值最高,随着时间推移逐渐下降至平稳状态严重度指标;初始状态为正常状态H时,指标值最低,随着时间推移逐渐上升至平稳状态严重度指标。 图4 不同初始状态严重度指标变化 TCSD-TCPST型移相器共有-13~13共27个档位可供调节。不同移相角度下,有功环流分布情况见表3所列。 表3 不同移相角度下有功环流状态 其中,单环流状态S环流路径为4.2节环流C1;多环流状态M环流路径为C1、C2、C3。 根据表3,计算不同移相角度下平稳状态严重度指标,计算结果如图5所示。 图5 不同移相角度下平稳状态严重度指标 由图5可知,移相器组态T=-13,-12,…,-9时,由于系统一直处于多环流状态,严重度指标高,达到0.212 8;T=-8,-7时,系统处于单环流状态或多环流状态,严重度指标较高;T=-6,-5,-4时,系统可能处于所有环流状态,严重度指标出现明显下降;T=-3,-2,…,13时,系统不存在有功环流,严重度指标为0。 本文定义有功环流严重度指标,该指标综合考虑了风电波动下不同环流状态发生概率及严重程度,可用于电网规划或运行调度合理性评估。得到如下结论: (1) 针对有功环流的马尔科夫链状态转移概率矩阵主对角线元素值明显大于两侧元素值,系统在短时间间隔内以较大概率维持上一时刻有功环流状态。 (2) 系统处于不同初始状态下,对比将来各时刻严重度指标:多环流初始状态始终高于单环流初始状态,单环流初始状态始终高于正常初始状态。最终都统一于平稳状态严重度指标。 (3) 调整移相角度构建的不同电力系统运行场景中,平稳状态严重度指标差异明显,可根据指标值合理配置移相器以规避环流风险,证明了所提指标用于环流评估的有效性及实用性。 本文仅考虑了风电出力波动对有功环流的影响,后续可加入负荷变化、发输电设备随机故障等,以完善该指标的研究。3 有功环流严重度概率评估
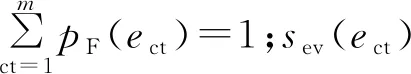
3.1 不同有功环流状态概率计算

3.2 不同有功环流状态严重程度计算
3.3 电力系统有功环流严重度概率评估
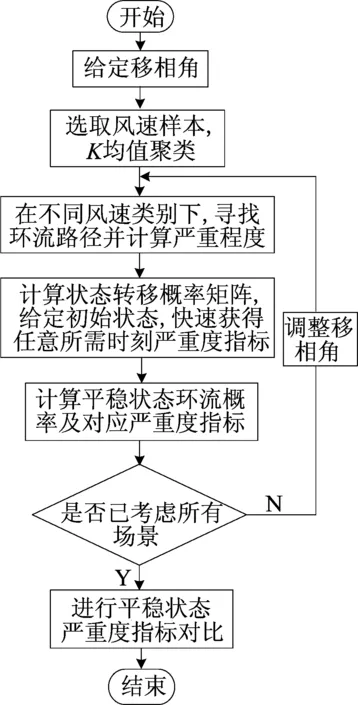
4 算例分析
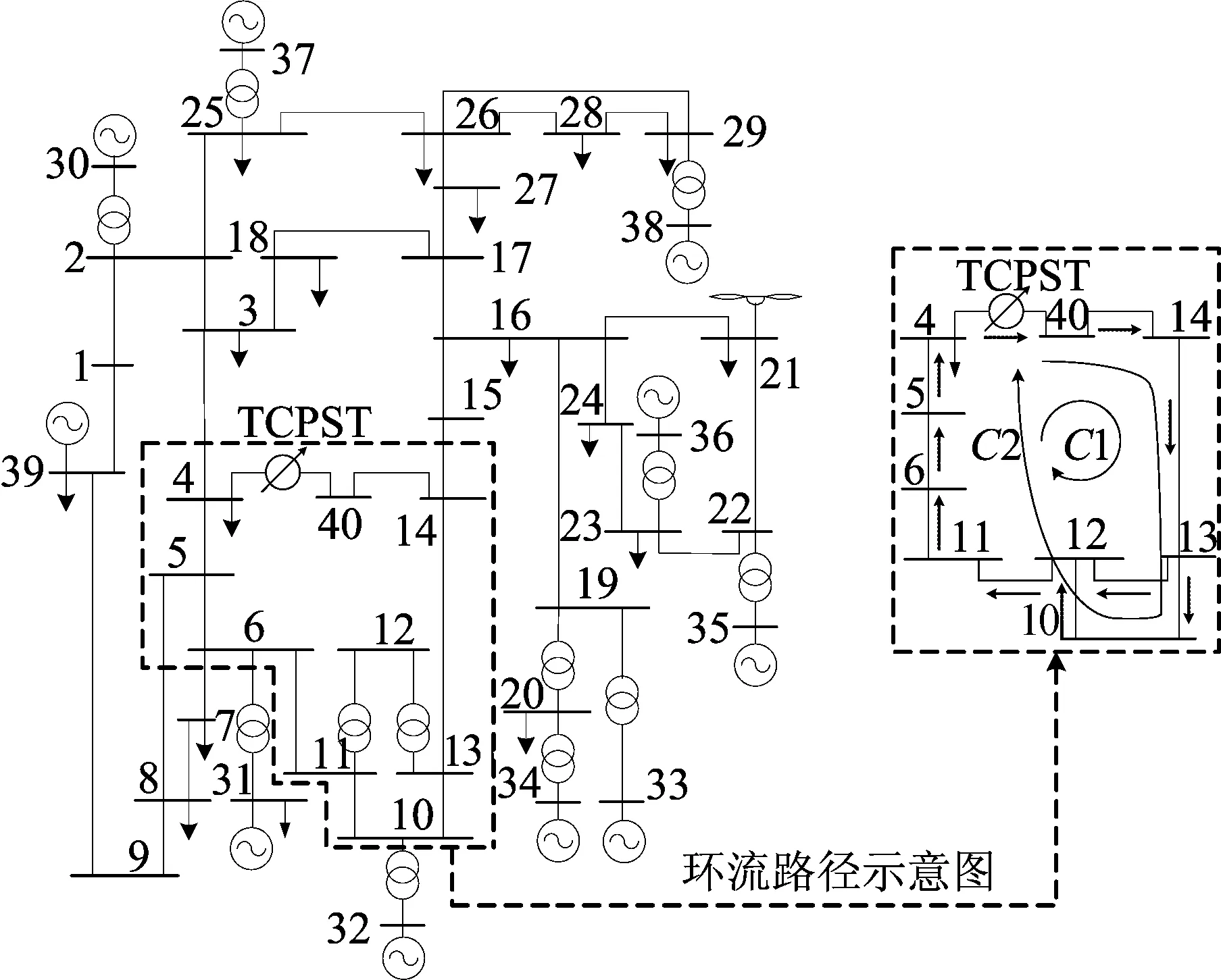
4.1 风速样本处理
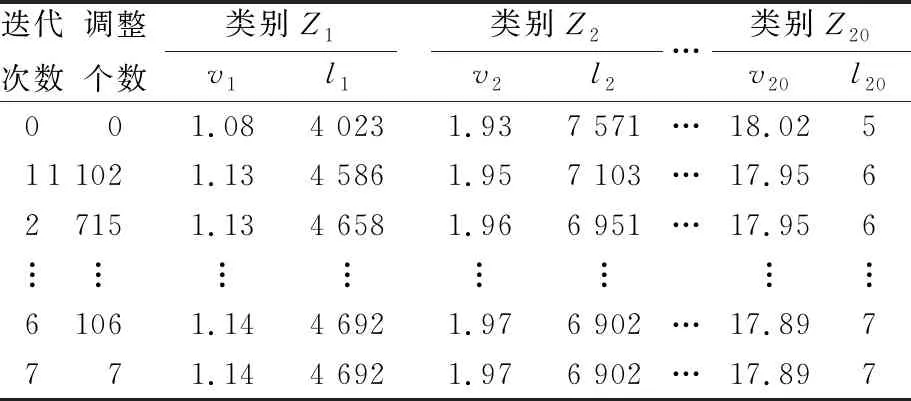
4.2 严重度指标计算

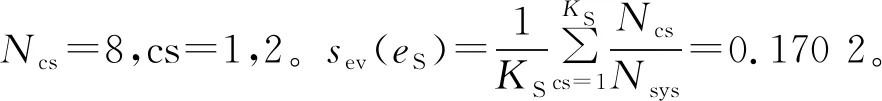
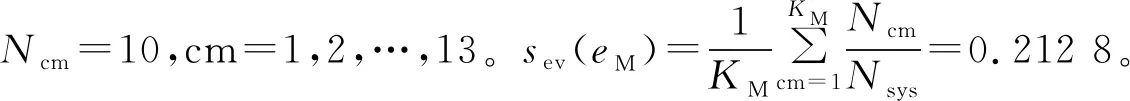
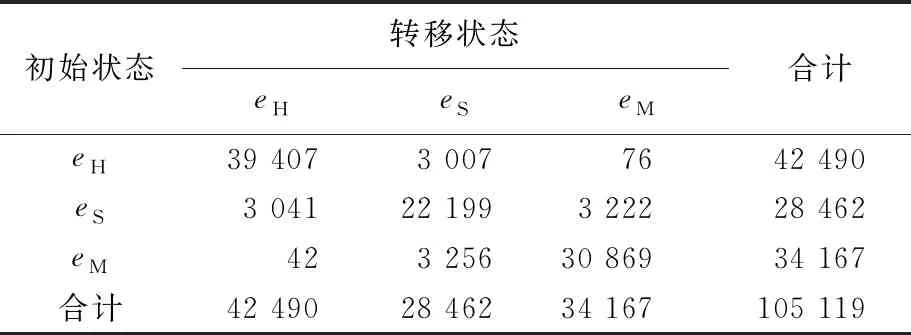

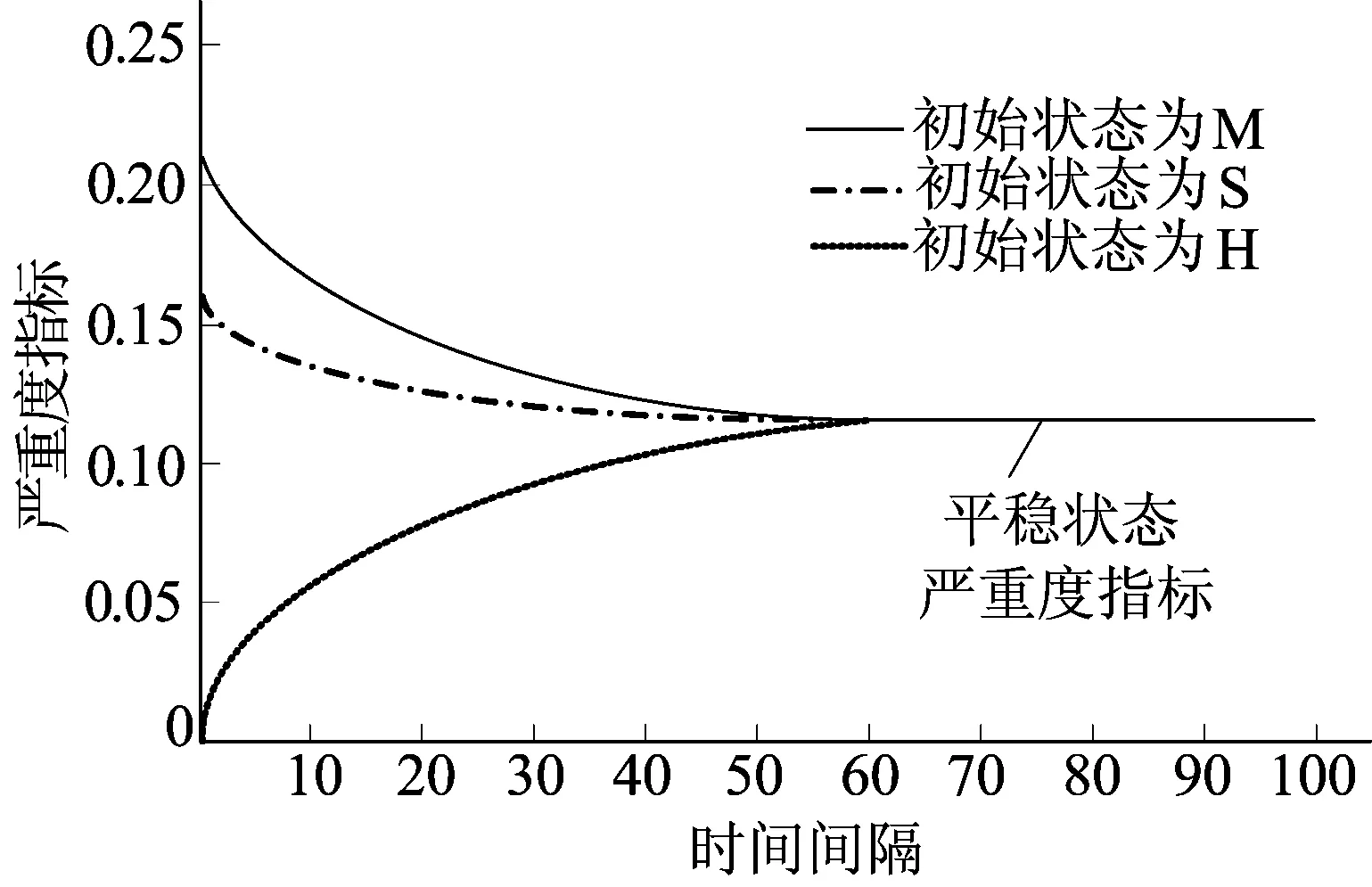
4.3 不同场景平稳状态严重度指标对比

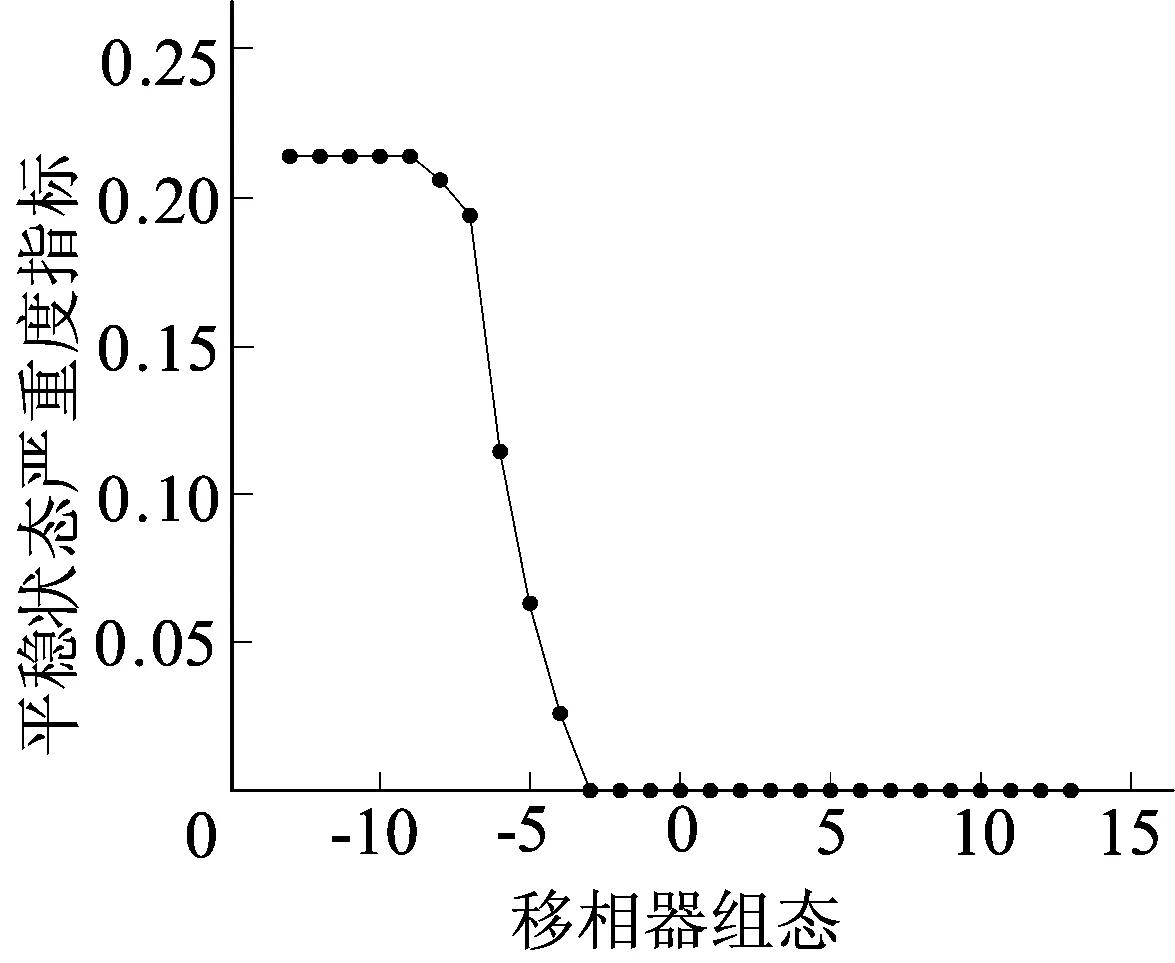
5 结 论

