基于遗忘因子的UKF车辆状态参数估计算法
冯亦奇, 陈 勇,2
(1.北京信息科技大学 机电工程学院,北京 100192; 2.北京电动车辆协同创新中心,北京 100192)
为车辆操纵稳定性控制系统在线提供精确的车辆状态参数是提高车辆操纵稳定性的前提。受目前技术水平限制,车辆某些重要状态参数(如车辆横摆角速度、质心侧偏角)需使用昂贵的传感器进行测量,增加了测量成本及制造成本。此外,车辆系统本身具有的高度非线性和时变性也是对车辆状态参数估计的主要挑战[1-2]。卡尔曼滤波方法采用递推迭代的形式,可对非线性模型进行有效处理并得到较为准确的估计结果[3]。
文献[4]以车辆轮速为输入信号,使用自适应卡尔曼滤波算法对车速进行在线估计;文献[5]基于二自由度车辆动力学模型,使用扩展卡尔曼滤波方法对车辆质心侧向速度进行在线估计;文献[6]以轮速作为输入信号,提出了一种经过改进的Sage-Husa扩展卡尔曼滤波方法,并对车辆状态参数进行了估计;文献[7]提出了将2个扩展卡尔曼滤波器并行滤波的方法,降低了车辆参数的变化对估计精度的影响;文献[8]利用模糊控制理论对测量噪声进行了在线实时调整,提高了算法鲁棒性。
本文提出了一种基于遗忘因子的无迹卡尔曼滤波(unscented Kalman filter,UKF)方法对行驶状态下的车辆参数进行估计。该算法以车轮前轮转向角、油门/制动踏板开度以及车辆侧向加速度传感器信号为输入信号,完成了对行驶状态下车辆的横摆角速度、质心侧偏角、质心纵向车速、质心侧向车速4个状态参数的有效估计;并通过CarSim与Matlab/Simulink联合仿真对所提出的滤波方法进行了对比验证。
1 车辆动力学模型建模
1.1 车辆模型建模
为了更精确地确定车辆运动状态,减小因模型误差而引起的过程噪声对滤波效果产生的消极影响,需要构建合理的车辆动力学模型。本文构建了包含纵向、侧向、横摆的三自由度非线性车辆动力学模型,如图1所示。

图1 三自由度车辆动力学模型
三自由度车辆动力学模型方程如下。
纵向动力学方程为:
max=(Fx11+Fx12)cosδ-(Fy11+Fy12)sinδ+Fx21+Fx22
(1)
侧向动力学方程为:
may=(Fx11+Fx12)sinδ+(Fy11+Fy12)cosδ+Fx21+Fx22
(2)
横摆动力学方程为:
a[-(Fx11-Fx12)sinδ+(Fy11+Fy12)cosδ]
(3)
其中,Iz为车辆绕Z轴的转动惯量;Fx、Fy分别表示车轮的纵向力、侧向力大小,其下标11、12、21、22分别表示前左轮、前右轮、后左轮、后右轮;tf、tr分别为车辆前轮轴距、后轮轴距。
根据(1)~(3)式,可求得三自由度车辆状态方程及其测量方程为:
(4)
(5)
其中,m为车辆整备质量;k1为前轮侧偏刚度;k2为后轮侧偏刚度;δ为前轮转向角;v为质心侧向速度;u为质心纵向速度;ωr为横摆角速度;β为质心侧偏角;ax为质心纵向加速度;ay为质心侧向加速度。
1.2 轮胎模型建模
轮胎是车辆与地面唯一发生接触的部件。对轮胎进行数学建模的精度,直接影响着整车动力学仿真的结果。本文采用“magic formula”魔术轮胎模型,其表达式为:
y=Dsin{Carctan[Bx-E(Bx-arctan(Bx))]}
(6)
Y(X)=y(x)+Sv
(7)
x=X+Sh
(8)
其中,B为刚度因子;C为形状因子;D为幅值因子;E为曲率因子;Sh为曲线在x轴上的偏移量;Sv为曲线在y轴上的偏移量;X为输入变量;Y(X)为输出变量。
(6)~(8)式中的各个参数均使用CarSim软件中所提供的魔术轮胎模型参数。魔术轮胎模型中的Y(X)可以是侧向力,也可以是回正力矩或纵向力,自变量X可以在不同的情况下分别表示轮胎的侧偏角或纵向滑移率,式中的系数B、C、D依次由轮胎的垂直载荷和外倾角来确定。
由三自由度车辆动力学模型可知,进行车辆状态预测时,需要已知轮胎的纵向力和侧向力[9]。用于计算轮胎侧向力和纵向力的输入量分别为轮胎侧偏角和轮胎纵向滑移率,其计算公式[10]可由车辆模型推导获得,即
(9)
(10)
其中,uij为各车轮中心速度,下标ij表示11、12、21、22,下文同;ωij为各车轮转动角速度;sij为各车轮纵向滑移率;αij为各车轮侧偏角;Y(X)为输出变量;hf为前轮轮距;hr为后轮轮距;re为车轮滚动半径。
2 基于遗忘因子的UKF滤波器设计
2.1 UKF原理
根据所建立的三自由度车辆模型,定义系统状态向量为X(t)=[ωrβu]T;定义系统输入向量为u(t)=[δax]T;观测量为y(t)=ay。车辆的系统状态方程为(4)式,观测方程为(5)式;在任意时刻t,非线性系统均可由含有高斯白噪声w(t)的系统状态变量X和含有高斯白噪声v(t)的观测变量Z(t)进行表示,即

(11)
其中,X(t)为状态向量;Z(t)为观测向量;u(t)为控制向量;f为系统状态转移函数;h为量测函数;w(t)为均值为q且方差为Q的系统过程高斯白噪声;v(t)为均值为r且方差为R的量测高斯白噪声。
UKF算法计算步骤如下所述。
(1) 计算获得1组采样点集(即Sigma点集)及其对应权值。无迹变化(unscented transform,UT)是UKF方法中的特有变换,它通过计算选取总数为2n+1个采样点(即Sigma点),再计算每点对应的权值,进而得到可以描述某一特定时刻下系统状态变量X(t)的统计特征。其中,n为系统状态向量X(t)的维数。Sigma采样点集及每个点所对应的权值计算公式为:
(12)

(13)
其中,λ为可对整体预测误差起到调整作用的缩放比例系数;下标m表示均值的权值,下标c表示协方差的权值。a的取值可以调整每次迭代UT变换中的采样点集分布状态;为了确保矩阵(n+λ)P为半正定矩阵,引入了可自行取值的待定系数k;不同于扩展卡尔曼滤波将Taylor展开式的高阶项直接忽略进而求得雅可比矩阵的方法,UKF引入了用来保留、合并方程中高阶微分项的非负权系数β。根据经验,对于正态分布的噪声,通常取β=2[7]。因此由(12)式、(13)式可以获得Sigma采样点集,即
(14)
(2) 计算Sigma采样点集的一步预测。计算公式为:
X(i)(k+1|k)=f(k,X(i)(k|k))
(15)
(3) 计算状态量的一步预测以及对应的协方差矩阵。由(14)式、(15)式加权求和得到系统状态量的一步预测以及协方差矩阵为:
(16)
X(i)(k+1|k)]×
(17)
其中,Q为系统过程噪声协方差矩阵。
在处理非线性滤波问题时,传统的扩展卡尔曼滤波方法在估计点处做Taylor级数展开,求得忽略高阶展开项的雅可比矩阵,再进行低阶近似计算。而UKF方法是在估计点处进行UT变换的,得到可以描述原系统状态向量X(t)均值、协方差2个统计特性的Sigma点集,再将其代入非线性方程进行计算,进而得到状态概率密度函数。这样不仅规避了对Taylor展开式中高阶项的直接计算,同时还提高了滤波精度。
(4) 根据一步预测值计算得到新的Sigma点集。计算公式为:
(18)
(5) 计算观测量预测值。计算公式为:
Z(i)(k+1|k)=h[X(i)(k+1|k)],i=1,2,…,2n+1
(19)
(6) 根据观测预测值,计算系统预测的均值和协方差。计算公式为:
(20)
PZkZk=
(21)
PXkZk=
(22)
其中,R为测量噪声协方差矩阵。
(7) 计算Kalman增益矩阵。计算公式为:
(23)
(8) 系统状态和协方差的更新。计算公式为:


(24)
P(k+1|k+1)=P(k+1|k)-K(k+1)PZkZkKT(k+1)
(25)
2.2 基于遗忘因子的UKF滤波器
在卡尔曼滤波方法中,反映模型误差的过程噪声协方差矩阵和信号测量中的测量噪声协方差矩阵对滤波效果的影响很大,在实际应用中,不仅无法对过程噪声进行精确估计,测量噪声也容易受到外界因素的干扰。因此,需对噪声协方差矩阵进行实时在线调整,使得过程噪声协方差阵和测量噪声协方差阵可以根据环境和系统运动进行自适应调节[11]。
本文建立的数学模型与实际系统间存在的模型误差和信号测量过程中由外界未知干扰源而引起的测量误差,是影响UKF滤波器滤波精度的2个主要因素。
此外,已有的文献中提供了如下经验结论:
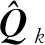
(26)
(27)
(28)
其中,ek为残差;b为遗忘因子。
遗忘因子b的取值范围通常为0.95~0.99[18]。为了防止UKF滤波器的估计效果对遗忘因子b的取值过于敏感,本文采用指数加权衰减方式 (1-b)/(1-bk),以保证滤波器的鲁棒性[18]。
本文通过CarSim与Matlab/Simulink联合仿真,对所提出的估计算法估计能力进行验证。CarSim与Matlab/Simulink联合仿真的框图如图2所示。
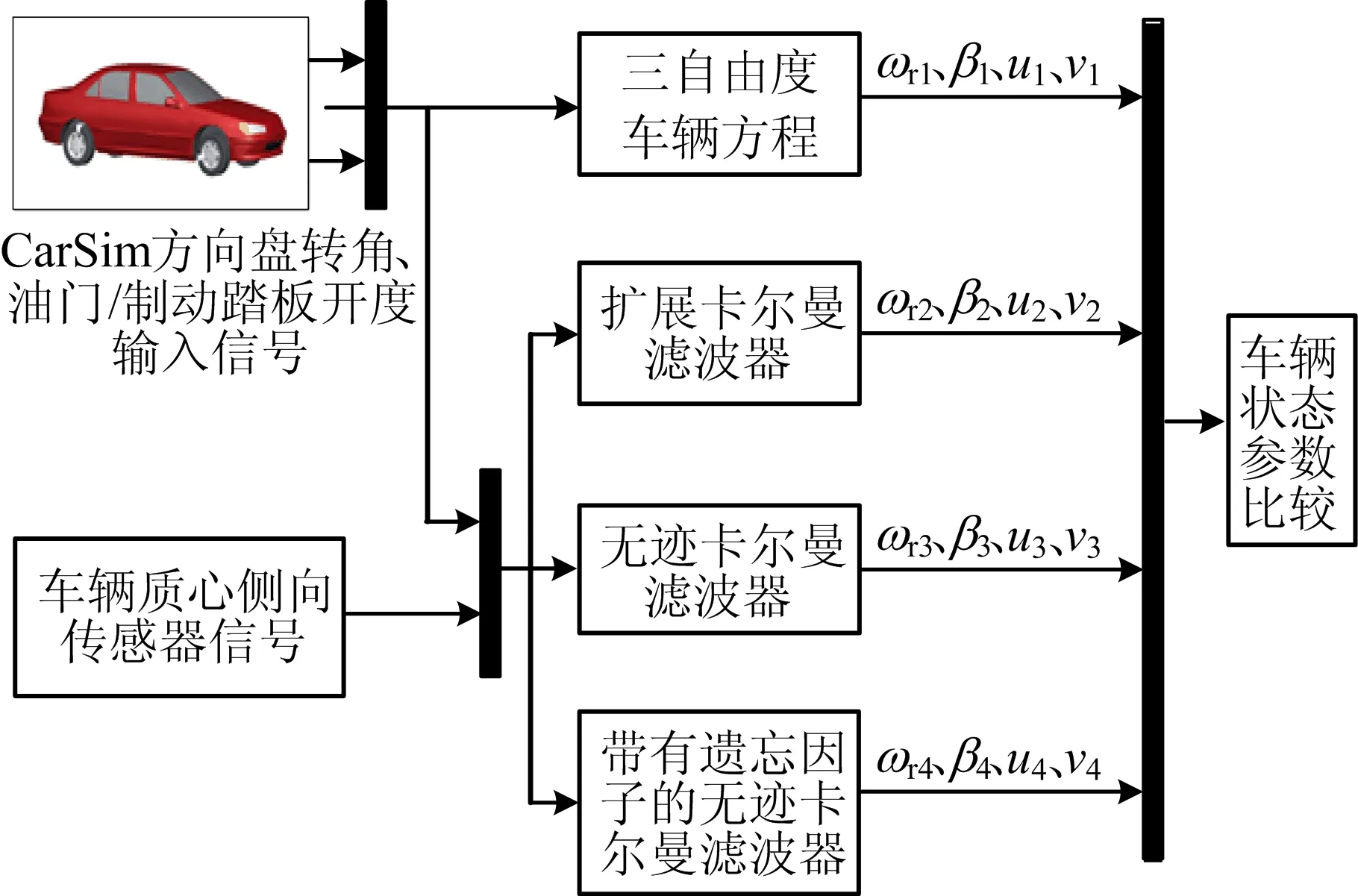
图2 CarSim与Matlab/Simulink联合仿真
3 仿真结果
以扩展卡尔曼滤波算法和UKF算法的滤波估计结果作为参照对象,对本文提出的基于遗忘因子的自适应UKF算法进行对比仿真验证。
在CarSim中车辆基本参数设置为:车辆整备质量m=1 458.5 kg;绕Z轴的转动惯量Iz=2 768 kg·m2;质心至前轴距离a=1.066 m;质心至后轴的距离b=1.544 m;前轴车轮侧偏刚度k1=-95 000 N/rad;后轴车轮侧偏刚度k2=-100 000 N/rad。
根据CarSim软件所提供的双移线工况数据,对算法的相关参数做如下定义:卡尔曼滤波器的系统状态向量为X(t)=[ωrβu]T,初始值设定为X-(t0)=[0 0 25]T,对应的车辆状态为以90 km/h的速度匀速直线行驶;系统输入向量为u(t)=[δax]T,其输入波形图如图3所示;观测量为y(t)=ay,其方差为3的时变高斯白噪声波形如图4所示;系统过程高斯白噪声协方差矩阵的初始值设置为Q0=I3×3;测量高斯白噪声协方差初始值设置为R0=1 000;误差协方差矩阵的初始值设置为P(t0)=I3×3;路面附着系数μ=0.8;采样周期为TSS=0.001 s。

图3 CarSim驾驶员输入信号波形

图4 含有时变白噪声的输入信号
3种滤波估计算法对车辆横摆角速度、质心侧偏角、纵向速度、侧向速度的仿真结果如图5所示。其中,EKF为护展卡尔曼滤波算法,AUKF为基于遗忘因子的自适应无迹卡尔曼滤波算法。从图5可以看出,相对于传统的EKF算法和UKF算法,AUKF算法具有更高的估计精度,并且其跟随性和鲁棒性良好。
由图5可知,本文所设计的AUKF算法在线调整量测噪声协方差矩阵Rk,有效降低了未知高斯白噪声对车辆状态参数估计的影响,使得改进的滤波算法对噪声有较强的抑制能力。
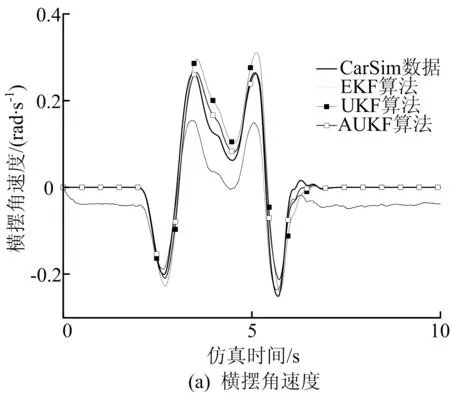
图5 3种滤波估计算法对各状态参数的仿真结果
为了对这3种卡尔曼滤波估计算法的估计精度进行定量比较,分别计算了3种卡尔曼算法的估计结果、CarSim数据值之间的平均绝对误差MAE和均方根误差RMSE,结果见表1、表2所列。
3种卡尔曼滤波估计算法的MAE和RMSE的计算公式如下:
(27)
其中,h(xi)为i时刻的观测估计值;yi为i时刻CarSim数据值。
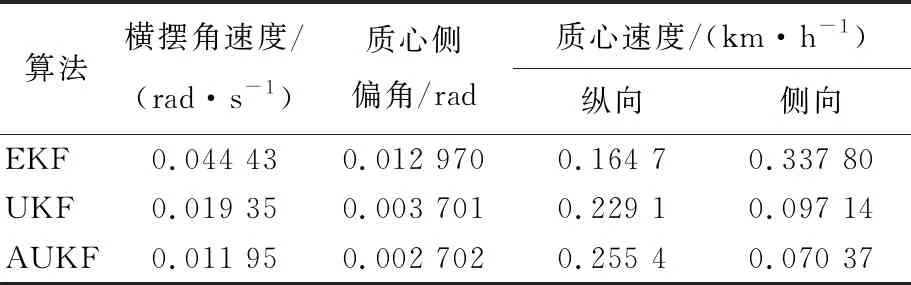
表1 3种算法的MAE指标

表2 3种算法的RMSE指标
由表1、表2可知,在对车辆横摆角速度、质心侧偏角和质心侧向速度3个车辆状态参数的滤波估计效果上,本文AUKF算法在MAE和RMSE 2个统计学评价指标上均优于传统的EKF算法和UKF算法,平均估计精度分别提高了38%、27%、28%;但在对质心纵向速度的估计精度,AUKF略显不足,仍需优化改进。
4 结 论
本文建立了以非线性三自由度车辆动力学模型和魔术轮胎模型相结合、用于车辆状态参数估计的数学模型;引入了遗忘因子的概念,对量测噪声协方差矩阵R进行在线调整,有效降低了未知高斯白噪声以及历史估计数据对车辆状态参数估计的干扰,使得滤波算法对未知噪声具有较强的抑制能力。
本文提出了估计精度更高的UKF滤波器与遗忘因子概念相结合的自适应UKF算法,实时在线估计车辆行驶状态下的状态参数,完成了在车辆行驶状态下对4个重要车辆状态参数的在线有效估计;并通过CarSim与Matlab/Simulink联合仿真对所提出的滤波方法进行了对比验证。
仿真结果表明,本文基于遗忘因子的UKF算法能更准确、稳定地估计车辆的行驶状态参数,为车辆动力学控制策略提供了可靠的车辆状态参数。

