高分辨率傅里叶变换光谱仪分束器补偿器的厚度匹配设计

陈 芳，高 超，白 杰

北京空间机电研究所，北京 100086

引 言

高光谱干涉技术以亚纳米级的光谱分辨率获取探测对象丰富的光谱信息，已被广泛用于遥感领域。 干涉光谱技术是利用干涉图与光源光谱图之间的对应关系，通过获取目标的干涉图并对其进行傅里叶变换，反演得到光谱图，从而获取光谱信息。 相对于传统的色散型光谱仪，从原理上解决了能量利用率低的缺陷，且具有多通道和高光谱分辨率的优点，是目前国际高光谱技术领域的研究热点之一，尤其是在红外遥感探测领域[1-3]。

日本的GOSAT和加拿大的ACE是目前在轨运行的用于大气遥感探测的傅里叶变换红外光谱仪[1-3]，与我国目前在研的高光谱分辨率傅里叶近红外光谱仪一样，都是迈克尔逊干涉仪型的傅里叶变换红外光谱仪。 该类傅里叶变换光谱仪采用迈克尔逊干涉仪原理，利用反射镜的移动产生光程差，并得到不同光程差下的干涉信号[4-5]。 为了提升光谱仪的分辨率和性能，前人的研究主要集中于移动反射镜运动误差引入的光程误差的影响，包括移动反射镜速度误差影响[6]，以及安装误差影响[7]，并提出通过将移动平面镜替换为角镜或楔形镜来消除运动与机械误差[5, 8-10]。

角镜式迈克尔逊干涉仪型傅里叶变换光谱仪结构如图1所示，两个角镜均安装在由同一转轴驱动的相互正交的摆臂上，通过摆臂摆动得到不同光程差下的干涉信号[10]。 在设计过程中，发现除了运动镜片的动态误差可以引入附加光程差外，分束器与补偿器的厚度匹配误差等静态误差也会影响光谱仪的精度和性能，对于应用于航天遥感领域的高信噪比要求的傅里叶变换光谱仪，其影响不可忽略。 本文对分束器与补偿器的厚度匹配误差对光谱仪的影响进行了详细的分析和计算，推导出分束器补偿器的厚度匹配误差的计算方法，进一步提升了光谱仪的精度与性能。

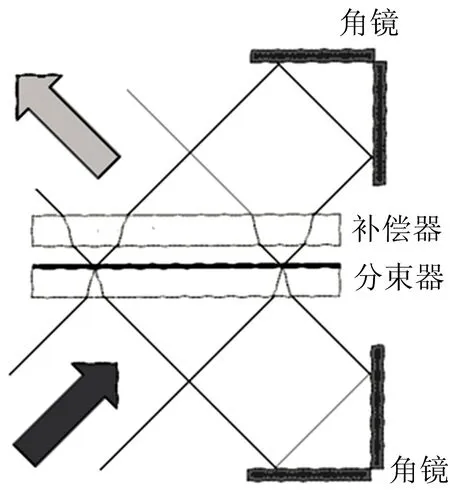
图1 角镜式迈克尔逊干涉仪光学结构图Fig.1 The optical structure of corner-cubemirrorMichelson interferometer

1 理论分析

传统的迈克尔逊干涉仪光学结构如图1所示，补偿器是为了减小分束器的色散对干涉效果的影响而加入的，因此要求补偿器与分束器在材料性能和厚度上完全一致。 材料性能可以从同炉的基底材料上进行控制，基本可以消除这一影响，而厚度因为加工精度影响，总是存在一定差异，这使得从分束面分开后的两束光所走过的光程不完全相同，导致干涉调制度的降低。

1.1 扩展光源的干涉信号

在理想情况下，分束器、补偿器厚度一致，点光源的干涉信号[11-12]为

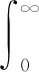
(1)

式(1)中，2RTB(γ)为光源的光谱函数，γ为波数，x为中心光程差。

(2)

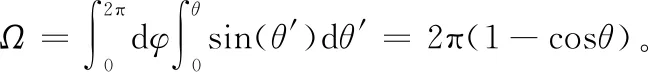
干涉信号的性能可以用调制度描述，调制度M定义为

其中Imax和Imin分别是干涉信号I(x,Ω)在不同中心光程差下的极大值和极小值，对于理想的傅里叶光谱仪，调制度M=1。

1.2 分束器与补偿器厚度不匹配引入的光程差分析

如图2所示，分束器和补偿器的几何厚度分别为d1和d2，空气间隙为d3，光线入射到分束器上的入射角为α，相应的折射角为β，分束器和补偿器的基底材料的折射率关于波数γ的函数为n(γ)。 则光路1与光路2在分束器和补偿器中走过的附加光程差为

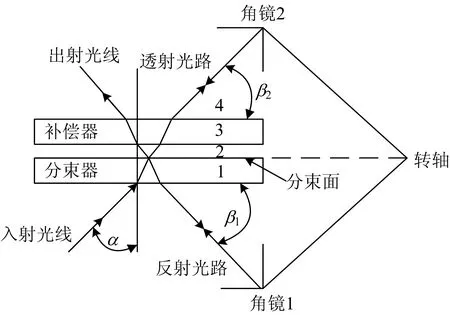
图2 迈克尔逊干涉仪结构示意图Fig.2 The structure of Michelson interferometer

分束器与补偿器的厚度差为Δd=(d1-d2)，根据折射定律，有sinβ=sinα/n(γ)，则分束器与补偿器厚度不匹配引起的几何光程差为

(3)

增加分束器与补偿器厚度不匹配所带来的光程差后，干涉信号为

(4)

采用波数为γ0的单色光源进行分析，则

(5)

2 厚度不匹配影响分析

分束器与补偿器厚度不匹配的厚度差Δd会引入新的几何光程差Δx，其会影响光谱仪的调制度(即光谱仪的性能)，由理论分析可知，入射角α、折射率n(γ)会影响厚度差Δd对光程差Δx的影响程度，因此分析厚度差Δd、入射角α和折射率n(γ)对光谱仪的性能影响是进行傅里叶光谱仪设计的基础。

我国在移动学习方面的研究，主要体现在理论和学习平台设计两个方面，经历了从理论到技术支持、学习平台到实践的过程，然后将移动学习应用到科学教学中，最后深入到课堂教学。事实证明，移动学习的到来对学生学习成绩提高有一定的成效，尤其在英语听读方面，不仅能培养学生学习的习惯，还能激发学生的兴趣、潜质，使其在语言情境中得以学习。［2］

2.1 厚度不匹配对光谱仪调制度的影响分析

对于实际应用中的傅里叶光谱仪，目标均为扩展光源，根据式(3)，在不同视场处，分束器与补偿器的厚度不匹配Δd引起的几何光程差不同，根据式(5)，对扩展光源全视场范围内的信号进行积分运算，得到扩展光源的干涉信号。 当分束器与补偿器厚度一致，即Δd=0，全视场范围的干涉信号关于中心视场圆对称，且当摆臂摆动引起的几何光程差x=0时，全视场范围的干涉信号同时达到峰值。 当分束器与补偿器厚度不一致，Δd不为零，全视场范围的干涉信号不再关于中心视场圆对称，由于相同立体角处的入射角不同，因此分束器与补偿器厚度差引起的几何光程差Δx与摆臂摆动引起的几何光程差xcosθ关于立体角Ω的变化趋势不一致，当摆臂摆动引起的几何光程差x=0时，全视场范围的干涉信号不再同时达到峰值，而是由于Δx的不同而出现条纹，从而使得光谱仪的调制度下降。

对分束器与补偿器的厚度差对光谱仪调制度的影响进行分析，设目标光源波数为γ=12 500 cm-1，视场角为θ=±5 mrad，摆臂摆动最大光程差为L=1.1 cm。 根据式(5)计算厚度差Δd对干涉信号的影响。 图3为不同厚度差Δd下，摆臂摆动引起的几何光程差x=0时全视场内的干涉图(利用zemax模拟仿真得到)。

图3 不同厚度差Δd下，x=0时全视场内的干涉图(zemax模拟)Fig.3 The interferogram of the whole fieldwhen OPD is zero (Zemax calculation)

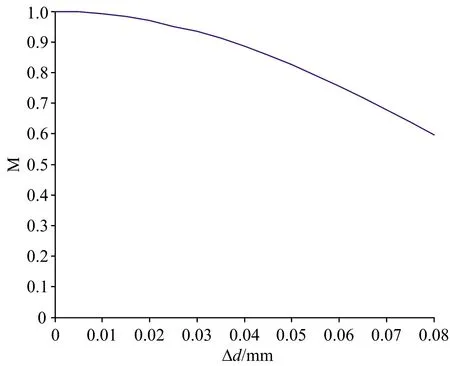
图4 光谱仪调制度随厚度差Δd的变化曲线Fig.4 Curve between thickness matching and modulation

根据以上分析，分束器与补偿器的厚度差引入额外的几何光程差使得总光程差不再关于中心视场圆对称，在理想最大值1时和最小值0时均出现干涉变化条纹，从而降低了调制度，而对光谱分辨率没有影响。 根据Zemax分析得到的视场内干涉图可以得到不同厚度差Δd下的光谱仪调制度曲线，如图4所示。 由图4可知，调制度的下降量是关于厚度差的递增函数，在设计过程中，需根据信噪比对调制度的要求来确定分束器与补偿器的厚度差的值。

2.2 视场角范围对厚度不匹配影响的增强效果

理想情况下，光源为点光源(视场半角θ=0)，分束器与补偿器厚度不匹配所带来的光程差是一个定值，只影响光谱仪零光程差位置，而不会影响干涉信号的调制度。 对于实际应用中的傅里叶光谱仪，不存在点光源，目标均为扩展光源，对于不同视场大小的扩展光源，分束器与补偿器厚度不匹配所带来的影响是不相同的。

对于迈克尔逊干涉仪，扩展光源视场为±θ，中心视场在分束器上的入射角为45°，则全视场内的入射角α的变化范围为(45-θ)～(45+θ)，入射角α的范围由视场半角θ确定。 对于非成像傅里叶光谱仪，θ一般为小量，不超过1°，在此量级范围内，光程差Δx是入射角α的递增函数，在视场范围内，光程差的变化值δ=Δxmax-Δxmin越大，表示视场范围内的条纹越多，则对干涉信号的调制度影响越大。

图5为波数γ=12 500 cm-1、不同厚度差Δd下光程差的变化值δ随视场半角θ的变化曲线。 视场半角θ越大，在允许调制度下降量相同的前提下，要求厚度差Δd越小，则分束器与补偿器的厚度加工精度要求越严格。 因此在傅里叶光谱仪设计时需综合考虑各个参数的设计。

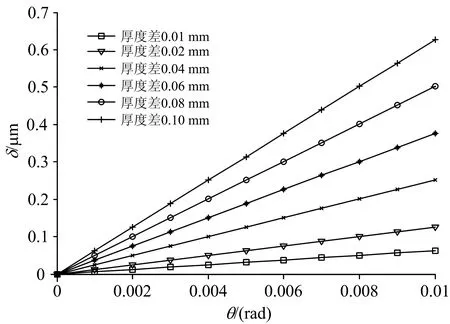
图5 不同厚度差Δd下光程差的变化值δ随视场半角θ的变化曲线(γ=12 500 cm-1)

2.3 色散对厚度不匹配影响的增强效果

对于某一材料来说，折射率n(γ)随波数γ变化。 由于光谱仪采用激光光路作为采样的基准，计量激光光路与光谱仪共光路，如果分束器与补偿器的厚度不一致，存在厚度差，目标光源的波数γ与计量激光的波数γ0在分束器补偿器中的折射率的差异将引入色散，造成二者的干涉图有一个相位差

(6)

若要使相位恢复明确，应当保持相位差小于2π[13]。

分束器和补偿器材料是石英玻璃，其折射率色散近似公式为

波长λ单位为μm。 图6为目标光源波数为12 500 cm-1、计量激光波数为7 633 cm-1时的色散相位差与厚度差之间的变化曲线，由图可知，为了满足相位条件(<2π)，分束器与补偿器的厚度匹配误差应小于0.053 5 mm。

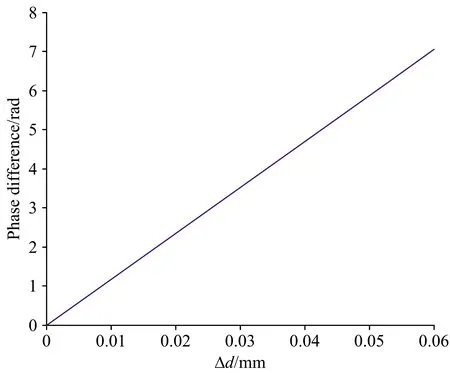
图6 色散相位差与厚度差之间的变化曲线Fig.6 Curve between thickness matching and phase difference

3 傅里叶光谱仪的厚度匹配设计准则

对一个用于地球温室气体检测的高光谱分辨率傅里叶变换光谱仪进行设计，光谱仪采用双角镜摆臂的迈克尔逊干涉仪原理，分光采用分光器补偿器方案，工作波长和光谱分辨率如表1所示，计量激光波长为1.31 μm。 根据信噪比指标分配要求分束器与补偿器厚度匹配公差所造成的调制度下降量小于5%，按照式(5)设计适用于此光谱仪的分束器与补偿器的厚度匹配公差。

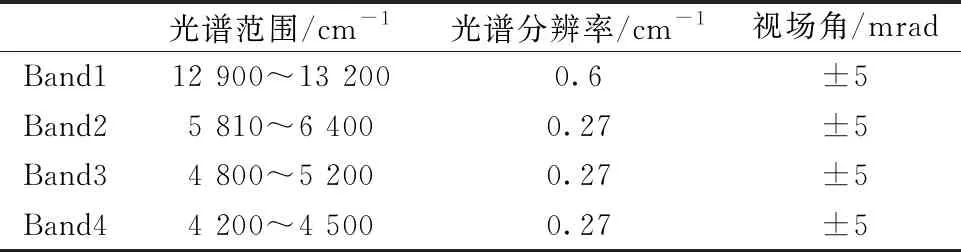
表1 高光谱分辨率傅里叶变换光谱仪参数Table 1 Design parameters of high spectralresolution Fourier interferometer

根据第3节的分析总结出分束器补偿器厚度匹配设计准则：

(1)根据相位匹配要求计算厚度匹配误差的最大值

根据2.3节色散影响分析，首先确定各谱段满足相位匹配要求的分束器与补偿器厚度匹配误差的最大值，如表2所示，可见，为满足与计量激光相位匹配的要求，分束器与补偿器厚度匹配误差应小于0.045 mm。

(2)根据调制度要求精确计算厚度匹配误差

根据式(5)计算分束器与补偿器厚度匹配误差小于0.045 mm时各谱段的调制度的变化曲线, 如图7所示。 可知，波数越大，调制度对分束器与补偿器厚度匹配误差越敏感，即波长越短，分束器与补偿器厚度匹配误差对调制度的影响越大。 根据分束器与补偿器厚度匹配公差所造成的调制度下降量小于5%的要求，分束器与补偿器厚度匹配误差应小于0.025 mm。

表2 各谱段分束器与补偿器厚度匹配误差的最大值Table 2 The allowed maximum value of thickness matching

图7 各谱段的调制度随分束器与补偿器厚度匹配误差的变化曲线Fig.7 Curve between thickness matchingand modulation in optical range

4 结 论

对采用分束器补偿器分光方案的傅里叶变换光谱仪的设计过程中，分束器补偿器厚度匹配误差对光谱仪调制度的影响进行了详细的理论分析和模型计算，分析了涉及的多个参数： 厚度差Δd、入射角α和折射率n(γ)对调制度的影响程度，总结了分束器补偿器厚度匹配误差设计准则： (1)根据工作谱段和计量激光波长的指标计算相位匹配所允许的最大厚度匹配误差； (2)在最大误差范围内确定符合信噪比对调制度的要求的厚度匹配误差值。 以一航天领域的高光谱分辨率傅里叶变换光谱仪为设计实例，得到了满足指标要求的分束器补偿器厚度匹配误差。 此种方法适用于采用分束器补偿器分光方案的傅里叶变换光谱仪。