融合重力信息的似大地水准面精化模型

沈鑫，胡伍生

东南大学 交通学院,江苏 南京 211189

0 引言

全球导航卫星系统(global navigation satellite system，GNSS)测量精度高、效率高，在工程实践中得到越来越广泛的应用。GNSS测量获得的高程为大地高HGNSS，起算面为椭球面。椭球面与似大地水准面不重合，大地高和正常高HNor之间存在高程异常ζ，计算公式为：

ζ=HGNSS-HNor。

(1)

GNSS测量获得的HGNSS已经具备较高精度，但工程中一般采用HNor，所以限制GNSS高程测量应用的主要因素是高程异常ζ的精度，似大地水准面的精化问题亟待解决[1-3]。

似大地水准面模型有多种[4-6]，其中二次多项式模型简单、拟合精度良好，应用广泛。本文以二次多项式模型为基础模型，提出一种融合重力信息的多项式模型，并利用神经网络的方法提出了融合重力信息的误差反向传播(error back propagation，BP)神经网络模型，对比分析两种模型的拟合精度。

1 二次多项式拟合模型

在常规的似大地水准面模拟方法中，模型自变量为经度和纬度，因变量是这一点上的ζ。文献[7]对似大地水准面模型的二次多项式拟合模型为：

ζ(x,y)=a0+a1x+a2y+a3x2+a4xy+a5y2

,

(2)

式中：a0为常数项，a1、a2、a3、a4、a5分别为经度、纬度及其二次项系数，x为经度，y为纬度。

因为ζ的变化与地理位置紧密相关，所以这种建模方式及参数的选取十分合理，是我国推荐采用的似大地水准面拟合手段。其建模参数较少，具备多余观测，可利用平差检验粗差点，即具备较好的抵抗粗差的能力。这种建模方式受个别ζ的影响较小，具备拟合多种地形条件的能力。

本文中二次多项式模型作为对比参照的基准，记作模型A。

2 融合重力信息的多项式模型

由于过去重力信息匮乏且精度不高，常规模型未将重力异常数据作为参数加入似大地水准面拟合模型中。重力异常数据是影响似大地水准面的因素之一，将其引入似大地水准面精化模型中，有利于提高模型的精度[8]。

利用重力恢复与气候试验(gravity recovery and climate experiment，GRACE)卫星跟踪数据、卫星测高数据和地面重力数据等多源数据建立地球重力场模型(earth gravitational model，EGM)2008。EGM2008的均方根误差为±11.137 cm，EGM2008的外部检核表明，EGM2008在全球范围内的误差为±13.0 cm，在美国的误差为±7.1 cm，在澳洲的误差为±26.6 cm。因此可以确定EGM2008在全球具有很高的精度。

在融合重力信息的二次多项式模型进行似大地水准面精化过程中，需要获取每一个试验点位的重力异常数据，而EGM2008提供网格点上的重力异常数据，所以需对EGM2008数据进行内插处理。

以常规二次多项式模型为基础，加入重力异常数据参数后得到一种融合重力信息的多项式模型：

ζ(x,y,g′)=a0+a1x+a2y+a3x2+a4xy+a5y2+a6g′+a7g′2

,

(3)

式中：g′为重力异常数据，a6、a7分别为重力异常数据的一次项和二次项系数。

式(3)在式(2)的基础上添加了重力异常数据的一次项和二次项，获得融合重力信息的多项式模型，记作模型B。

3 基于神经网络的融合模型

随着人工智能的发展，神经网络方法在模型拟合精化方面的应用越来越广泛[9-12]，本文即在模型B的基础上，提出一种基于神经网络的融合模型。

3.1 神经网络BP算法

BP算法是一种基于样本训练，自我学习调整的神经网络模型，该模型自20世纪70年代提出以来，经过几十年的发展，已经被证明适用于多个领域。BP神经网络模型结构如图1所示。

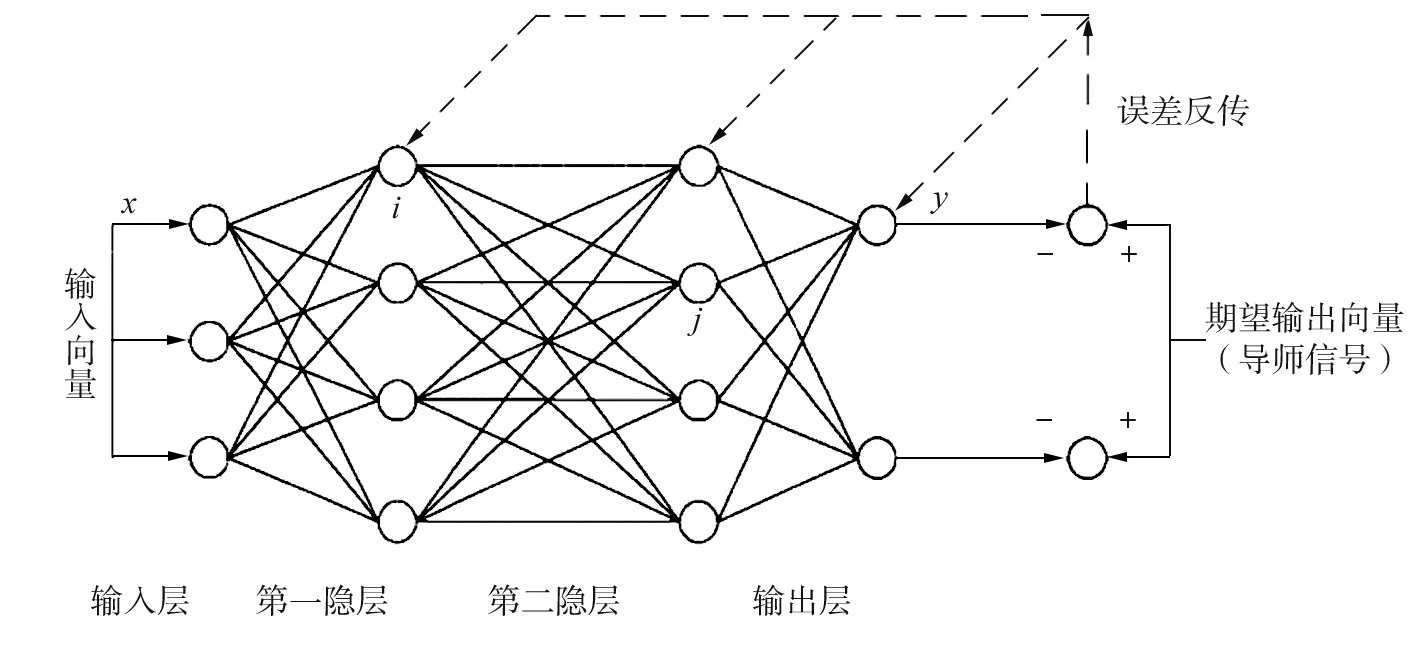
图1 BP神经网络模型结构

由图1可知，BP神经网络主要由输入层、隐含层和输出层3部分构成。输入向量和输出向量对应常规模型中的自变量和因变量。BP神经网络需要训练建模，训练过程分为正向传播过程和误差反向传播过程。正向传播过程中，输入向量经过与权值矩阵的运算，进入多层隐含层，隐含层之间均由权值矩阵连接，直至所有隐含层运算结束，得到输出结果。输出结果与期望输出结果的误差作为训练信号，对权值矩阵进行逐层调整，使输出结果的误差变小。通过多个样本的学习，BP神经网络可以得到合适的权值矩阵，输入向量经过传播运算即可得到达到期望精度要求的输出向量。这既是BP神经网络的学习过程，也是建模过程。用试验数据检验BP神经网络的学习成果，即可判定学习效果[13-15]。

图2 融合重力信息的BP神经网络模型结构图

3.2 融合模型

基于神经网络的8参数融合模型如图2所示。

图2融合模型的输出层参数除了代表二次多项式参数的x、y、x2、y2和xy外，加入了代表重力异常数据的一次项和二次项g′和g′2，还加入了ζB，是由模型B计算得到的ζ估计结果。输出参数为ζ-ζB，是模型B拟合似大地水准面的残差，记作模型C[16-19]。

在输入层加入ζB是因为模型B的综合性质优良，即综合了二次多项式和重力信息，对模型精化有增益效果[20-23]。

输出层参数变为残差输出参数ζ-ζB，只是原输出参数减去ζB即为原输出参数高程异常。模型B可使似大地水准面的拟合精度较高，即拟合残差ζ-ζB远小于ζ。神经网络数据处理软件在计算前对数据进行归一化处理，使结果相对较小，因此预处理数据有益于模型精化[24-25]。

4 工程实例分析

4.1 试验数据的来源与处理

试验数据来源于某地区，原始数据包含经度、纬度，重力异常数据由EGM2008地球重力场数据内插计算获得，如图3所示。

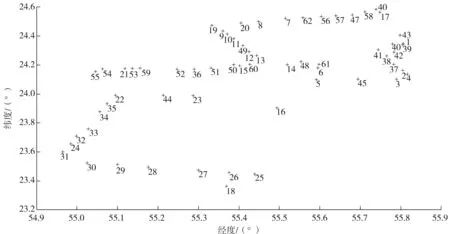
图3 工程实例点位分布图

工程中共有62个点位。试验地区经度跨度为0.853°，纬度跨度为1.221°，工程面积接近10 000 km2，其成果可供市级似大地水准面精化参考。为保护数据源，已对原始数据进行加密处理，但不影响分析结果。

为确保试验有效性，首先筛选原始数据。试验中利用中误差判断数据质量，各点位ζ均为已知，故得到中误差

(4)

式中：Δi为真误差，即模型估计值与实测ζ之差；n为参与建模的点位个数。

用本试验的全部数据建立模型A，得到全部点位ζ的拟合结果，计算m，剔除点位误差超过3倍m的点。经粗差剔除，去掉3号和19号点，得到60个试验点，均匀选取其中20个作为基准点，用来建立不同的模型，其余40个点作为检验点，用来比较不同模型的拟合效果。

4.2 模型建立与检验

4.2.1 模型A

模型A采用Matlab软件建模，得到基准点与检验点残差如表1、2所示。

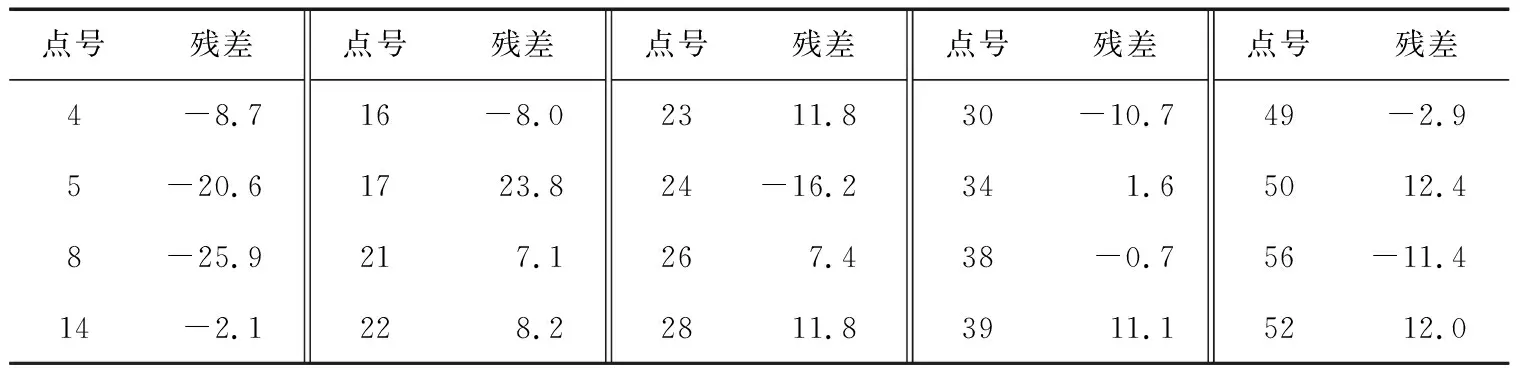
表1 模型A基准点残差 cm

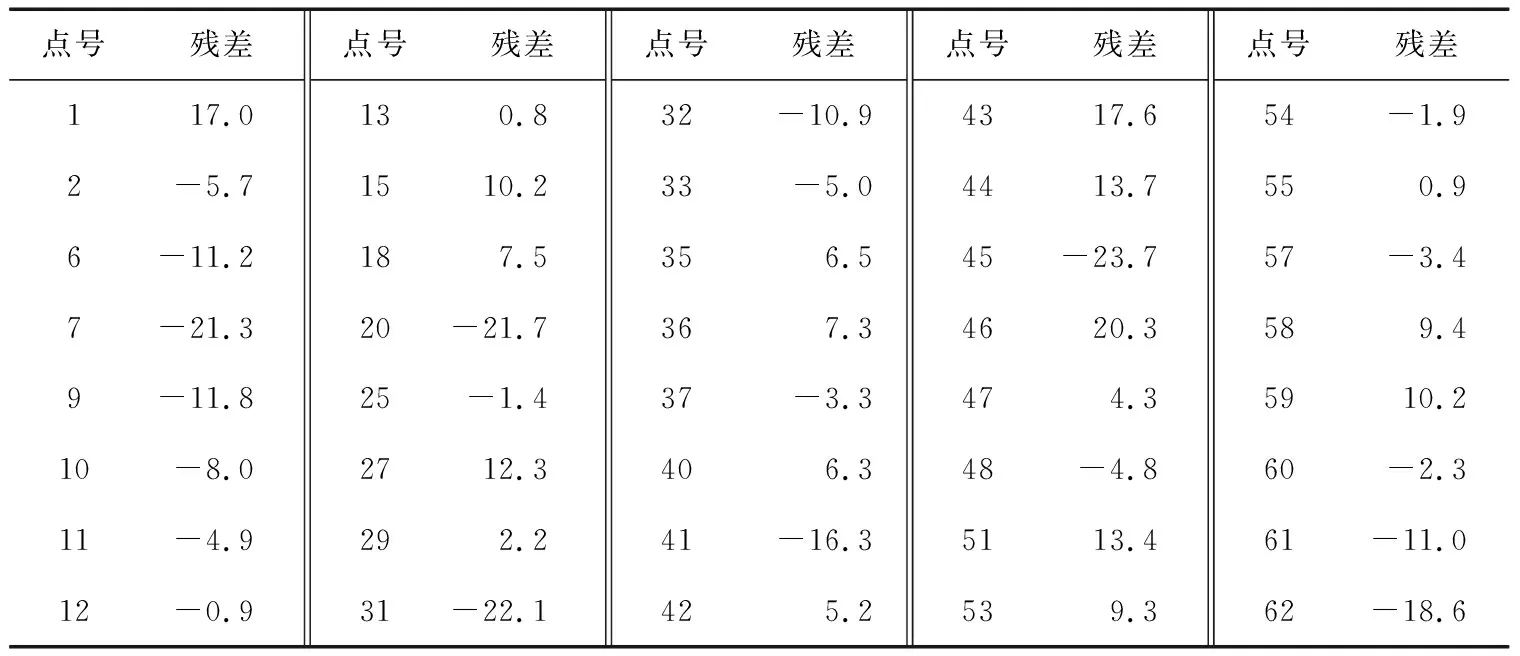
表2 模型A检验点残差 cm

由表1可知：在二次多项式模型基准点中， 38号点的残差的绝对值最小，残差为-0.7 cm； 8号点的残差的绝对值最大，残差为-25.9 cm，m=12.6 cm。

由表2可知:在二次多项式模型检验点中，13号点残差的绝对值最小，为0.8 cm；45号点残差的绝对值最大，残差为-23.7 cm，m=11.7 cm。

4.2.2 模型B

模型B采用Matlab软件建模，得到基准点与检验点残差如表3、4所示。

由表3可知:在融合重力信息多项式模型基准点中，52号点残差的绝对值最小，残差为0.3 cm；50号点残差的绝对值最大，残差为7.6 cm，m=3.8 cm。由表4可知：在融合重力信息多项式模型检验点中，18号点残差的绝对值最小，为0.2 cm；41号点残差的绝对值最大，残差为-15.7 cm，m=4.3 cm。

4.2.3 模型C

模型C采用神经网络数据处理软件建模，在输入文件中，输入层参数为x、y、x2、xy、y2、g′、g′2、ζB，输出层参数为ζ-ζB。

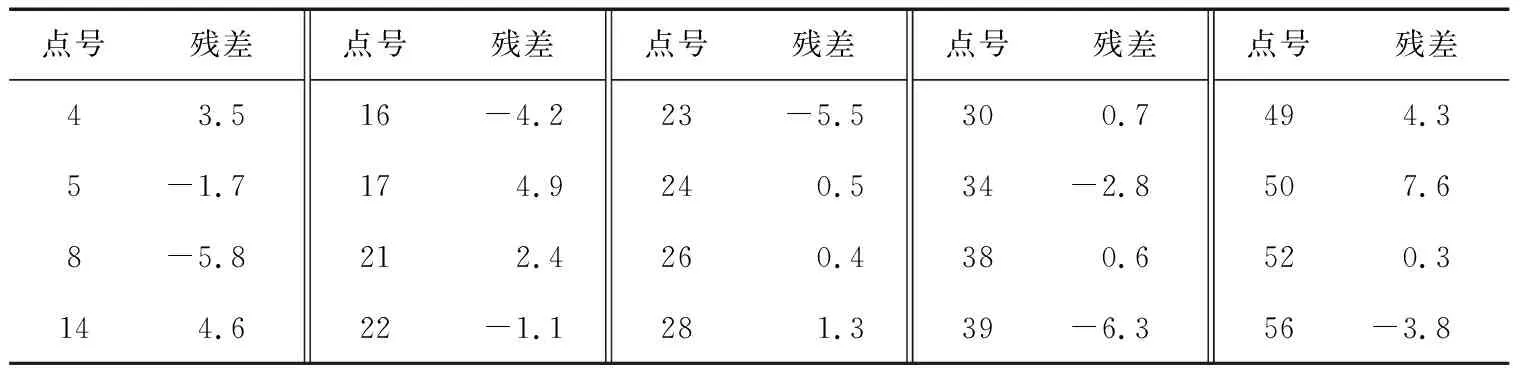
表3 模型B基准点残差 cm

表4 模型B检验点残差 cm

神经网络学习的随机性质(连接权值矩阵的随机初始化)决定每一次的学习结果在一定范围内波动。所以评价一个神经网络的学习效果时，不仅要估计其拟合精度，也要考虑其稳定性，在参数设置相同的条件下，其多次拟合结果之间的差别应较小。

神经网络数据处理软件设置了多项可调参数，根据参数意义和神经网络模拟试验表现进行具体调节，应用相同的基准点和检验点数据，在进行了约100次神经网络模拟试验后，得到最优设置参数如表5所示。

表5 模型C最优设置参数

以表5的最优设置参数进行10次试验，其拟合结果如表6所示。

表6 模型C的试验结果cm

由表6可知：10次试验的基准点平均中误差为1.7 cm，检验点平均中误差为3.9 cm，因为检验点平均中误差与第10次试验十分接近，而检验点中误差是评价似大地水准面精化水平的重要指标之一，故选取第10次试验数据作为参考，模型C基准点及检验点的残差如表7、8所示。

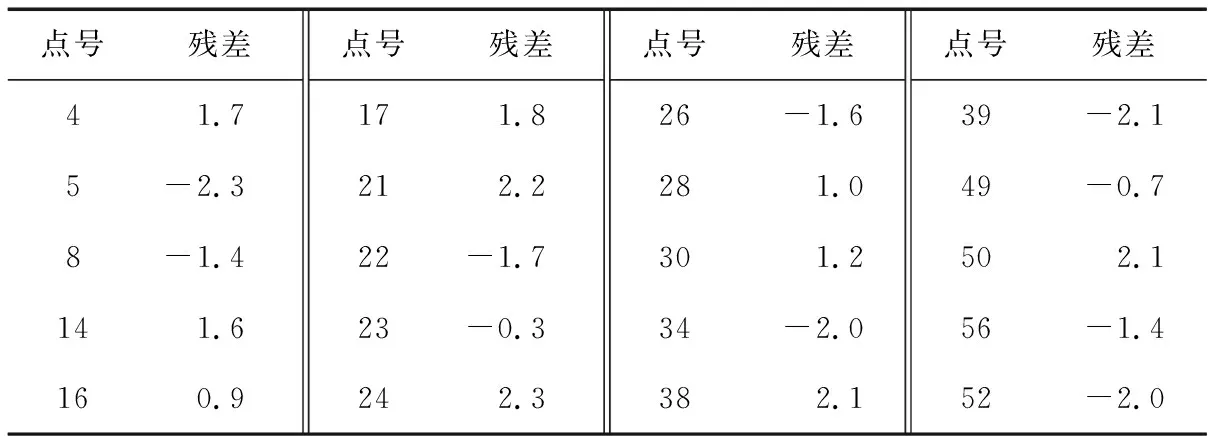
表7 模型C基准点残差 cm

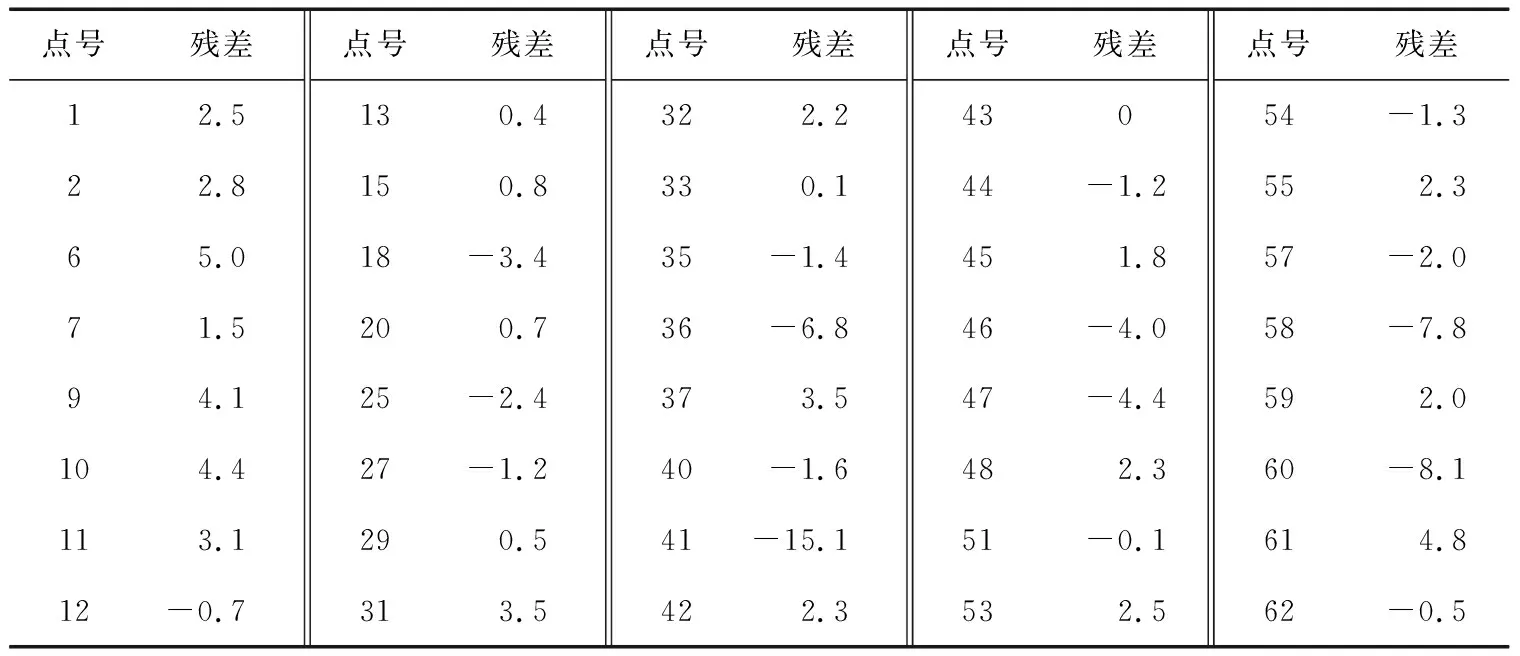
表8 模型C检验点残差 cm

由表7可得：23号点残差的绝对值最小，残差为-0.3 cm；24号点残差的绝对值最大，残差为2.3 cm，m=1.7 cm。由表8可得：43号点残差的绝对值最小，残差为0；41号点残差的绝对值最大，残差为-15.1 cm，m=4.0 cm。

4.3 拟合效果对比分析

对比3种模型的拟合精度可知，以检验点中误差为准，模型B的精度比模型A提升约60%，模型C的精度比模型A提升约65%，说明EGM2008数据对似大地水准面的精化有明显的提升效果，但神经网络的方法提升效果更好。

5 结论

1)EGM2008重力异常数据与ζ关系紧密，因此，在似大地水准面的二次多项式拟合模型中加入EGM2008重力异常数据，能明显提升模型的拟合效果。

2)以二次多项式拟合模型为基础建立的2种似大地水准面精化模型均有较好的拟合效果，其中应用融合重力数据的BP神经网络8参数模型的拟合精度可提升65%，应用效果良好，有一定的推广价值。