离网型风光储互补系统能量管理研究

马紫琬，高仕红，汤 洋，黄 京，陈 谦，董岳昆

(湖北民族大学 信息工程学院，湖北 恩施 445000)

随着温室气体过量排放，环境问题日益加剧，可再生能源成为各国青睐的发展目标能源.与传统单一能源相比，目前多能源互补已成为发展趋势，提出了利用综合能源系统降低供应成本问题[1]，推动可再生能源发展[2-3].国内外科研工作者致力于解决可再生能源存在的耦合现象和不确定性能源优化问题.对于单能源优化，宁阳天等[4]通过建立粒子群算法维持功率平衡并获得最低经济，但没有考虑系统的随机性；Piperagkas G S等[5]研究了风力发电系统的优化问题，考虑风力发电与负荷的随机性并采用粒子群优化算法求解运行费用最小运行问题，然而没有考虑多能源结合情况.对于多能源优化，顾伟等[6]、王成山等[7]研究了冷热电联供和分供对比得出特殊日的最优运行方式，但是没有兼顾系统的经济性；为了解决此问题，张晨迪等[8]研究了在孤网运行情况下引入博弈论来提高系统运行经济性；张海涛等[9]研究了针对多目标优化提出多时间多尺度的能量优化管理调度策略，然而只研究了系统给出的参考数据，没有考虑系统实际情况；朱晔等[10]研究了微电网冷热电在线运行并提出了基于微网状态空间的集中预测模型，由于缺少日前调度并不能考虑全局最优性；章子涵[11]、何畅等[12]研究提出了MPC(model predictive control)算法对日前预测结果进行实时能量优化，但缺少实时反馈环节，不能对偏差进行矫正.

通过对传统微电网能量管理的研究发现MPC控制存在以下不足：① 系统的参考电价直接影响各设备运行；② 模型预测控制策略具有非线性特征；③ 蓄电池频繁的充放电导致使用寿命缩短.针对上述不足，提出基于模型预测控制的离网型风光储互补能量优化管理策略，该控制策略采用混合整数线性规划方法构建包括运行成本、维护成本及违约成本的经济最小值目标函数，建立日前模型预测、日内模型预测和反馈矫正的优化模型，在兼顾全局经济最优的同时平抑系统功率波动，搭建全局离线、局部滚动优化及实时反馈的优化算法.

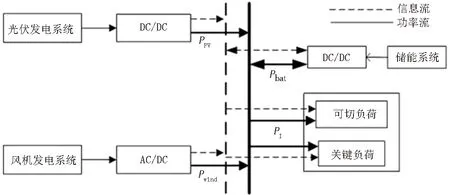
图1 风光储互补系统结构Fig.1 Structure diagram of wind/solar/battery hybrid power system

1 风光储互补系统的预测模型

1.1 风光储互补系统及结构

离网型风光储互补系统的基本结构包括风力发电系统、光伏发电系统、储能系统及全部负荷，系统的运行控制和优化管理分别由功率流和信息流来交互，其系统结构如图1所示.

1.2 预测模型

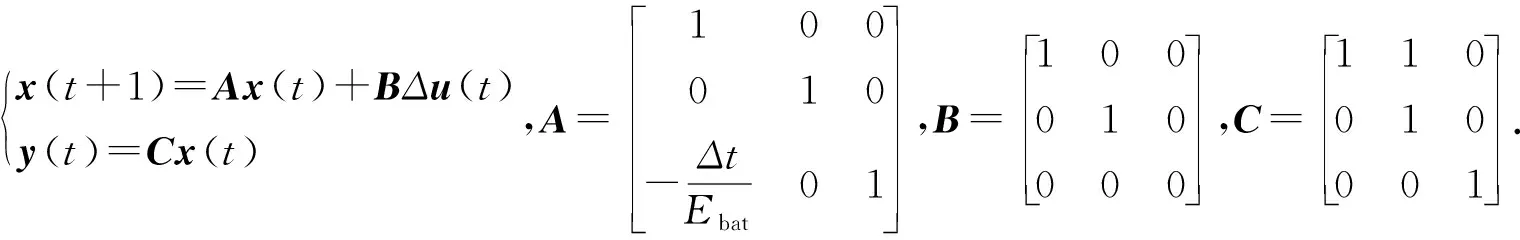
1.3 目标函数

考虑到微电网的安全和经济运行，系统控制目标主要为蓄电池系统的维护成本、切除负荷违约成本和储能系统惩罚成本.蓄电池系统的维护成本：满足负荷需求和维持系统功率平衡，保证风光储单元正常运行.切除负荷违约成本：在储能系统安全限值内减少切除负荷的次数，提高独立运行能力.储能系统惩罚成本：避免频繁的充放电导致使用寿命缩短，保持蓄电池的理想荷电状态.

(1)

(2)

(3)

(4)

其中，Mbat为蓄电池维护参考单价，MI为切负荷违约参考单价，γ为蓄电池惩罚因子，一般取值为0.714元/(kW·h)[13]，|Pbat,t|为储能系统功率交换值，|PI,t|为切除负荷值.

1.4 约束方程

1) 蓄电池储能约束方程.当系统功率富足时，蓄电池将其储存起来；当系统功率短缺时，蓄电池对系统供能.

充放电状态约束方程：

Uchr,t+Udis,t≤1，

(5)

Ebat,t=Ebat,t+ηPbat，tΔt，

(6)

(7)

Pbat,min≤Pbat(t)≤Pbat,max，

(8)

Pbat,min=-Pbat,max，

(9)

SOCmin≤SOC(t)≤SOCmax，

(10)

(11)

Ebat,min=Ebat,0×SOCmin.

(12)

其中，Uchr,t与Udis,t分别用0-1代表蓄电池启停，Ebat,0为蓄电池额定容量,ηchr,t和1/ηdis,t分别为充放电效率，Pbat,min和Pbat,max分别为蓄电池的上下限值，SOCmin和SOCmax为荷电上下限值.

2) 功率平衡约束方程：Ppv，t+Pw，t+Pbat，t=Pload，t.

(13)

其中，Ppv，t、Pw，t、Pbat，t与Pload，t分别为光伏、风机、蓄电池及全部负载功率.

图2 模型预测控制优化结构图Fig.2 Structure diagram of model predictive control optimization

2 基于模型预测控制的能量优化管理策略

2.1 模型预测控制优化策略

模型预测控制优化策略结构如图2所示，包含日前预测、日内预测及反馈矫正三部分.系统的预测精度与时间跨度成反比，通过采集历史信息和模型信息对目标函数滚动优化.日前预测控制：根据系统参考电价和负荷需求信息并结合目标函数及约束方程获得24 h的蓄电池启停状态、微电网与负荷之间的交互功率及运行成本.日内预测控制：从t时刻起，利用实时数据经过P时段运行对风机、光伏和负荷进行预测并调整日前数据，在t+1时刻开始下一轮滚动优化.反馈矫正：根据参考值与实时预测数据的偏差对系统运行状态调整.

2.2 混合整数线性规划问题转化

采用混合整数线性规划方法便于对MPC优化问题求解，通过引入δ(t)和连续辅助变量z(t)=δ(t)P(t)，将变量转换成混合整数线性规划问题，在Matlab环境中外接yalmip优化器求解混合整数线性规划问题，获得目标函数的最优解，令：

Pbat,t≥0 ⟺δbat,t=1，

(14)

Pbat,t=Pbat,tδbat,t+Pbat,t(1-δbat,t) .

(15)

则式(2)、(3)、(4)、(6)、(7)转化为：

Cbat=Mbat[2zbat,t-Pbat,t] ，

(16)

CI=MI[2zI,t-PI,t] ，

(17)

(18)

(19)

3 算例分析

为证明控制策略的可行性和有效性，对离网型风光储互补能量优化管理系统进行仿真验证.风光储互补系统参数参考文献[13]的数据，其中风电机组额定功率为300 kW，光伏额定功率为800 kW，蓄电池的额定功率为800 kW、额定容量为2 500 kW·h.图3和图4给出了风光储互补系统各时段的功率值和参考电价.

图3 光伏、风机和负荷数据图图4 维护与惩罚参考电价数据 Fig.3 Wind turbines,photovoltaic load data graph Fig.4 Maintenance and penalty reference price data

表1 日前预测和日内预测控制总运行费用Tab.1 Total operating costs of day-ahead forecast and within-day forecast control

分析日前与日内模式对经济性的影响.采用基于日前预测、日内预测控制方法分别将24组与48组实际数据进行实时滚动求解得出平均运行成本，计算出运行经济费用为987.304 2元与952.706 2元，如表1所示.由表1的数据可分析到，日内预测相比较于日前预测在运行成本上减少了34.598元，原因在于前者基于离线全时段优化，误差比较大，通过蓄电池的充放电来减少偏差；而后者是基于日前计划引导进行滚动优化运行，并考虑预测数据的不确定性，通过采用闭环矫正环节降低预测误差对经济性的影响.

由于系统设备的启停直接影响系统的经济运行成本，日前预测控制充放电状态如图5所示.由图5可看出，蓄电池充电状态与放电状态总时间相等，当光伏和风力发电系统不足，储能系统对微电网进行充电，起到削峰填谷的作用.蓄电池容量曲线如图6所示，结合图5可看出蓄电池充放电状态随容量变化，在前4时容量保持恒定，分别在5、10、16和21时处蓄电池因风机电能减少向系统供能，22时因负荷需求减少而储存能量.在一天时间内，蓄电池容量在日前与日内控制策略中分别产生了13 172.642 6 kW·h与14 575.076 2 kW·h的变化，对比得出日内预测能快速对负荷变化做出调整.

图5 日前预测控制充放电状态变化曲线图6 蓄电池容量日前、日内及反馈矫正曲线

图7 蓄电池功率日前、日内及反馈矫正曲线图8 负载功率日内与反馈矫正曲线

由于风光储互补系统具有随机性，微电网在模型预测控制策略下的计算结果如图7和8所示.在3、10、15和19时处负荷需求波动变大，MPC根据上一时的历史数据求出系统最优解作为下一时的预测参考值，负载需求波动曲线直接影响蓄电池功率变化.日内预测相比较于反馈矫正负荷功率波动在限值范围内，运行费用为952.706 2元,日内预测控制更稳定.

4 结语

本文提出了基于模型预测控制的离网型风光储互补能量优化管理策略，MPC通过引入逻辑变量和连续变量将目标函数与约束方程转化为混合整数线性规划问题，以便于yalmip求解得到最优功率控制序列.基于模型预测控制框架下设计光伏、风机、蓄电池及参考电价等数据的仿真结果表明，该策略可降低不确定性对能量优化管理的影响，并提高系统运行的经济性.