基于Barzilai-Borwein梯度法的多微电网系统递阶优化调度算法

郑鹏远，李 琴，孙忠林

(上海电力大学自动化工程学院，上海 200090)

微电网是由多种分布式电源、储能单元、能量转换装置、负荷以及控制、保护装置构成的系统单位[1-3]。微电网是一个小型的发配用电系统，为分布式电源提供良好的接入平台，可以有效地消纳和管理各种形式的分布式电源。微电网可根据微电网自身供求及大电网的状态选择工作于并网运行模式或离网运行模式。邻近的微电网通过相互交换信息和电能形成互联的多微电网系统，通过微电网间的协调互补可以进一步提高电网运行的稳定性，降低微电网的运行成本。由于多微电网系统维数高、关联复杂，如何实现多微电网系统的经济性优化且提高优化效率日益受到人们关注。

随着微电网技术的发展和成熟，微电网的建设日益增多，微电网间的关联日益紧密，如何提高邻近微电网间的协调水平，从而整体提高微电网运行经济性能成为多微电网规划、设计及建设的核心问题之一。合理的多微电网优化配置不仅能够提高各分布式电源的利用效率，还能供电可靠性，降低微电网运行成本。文献[4]基于MAS的分层结构提出了基于多代理的多微网能量协调算法，实现多微电网的能量管理；文献[5]针对微电网群，使用交替向量乘子法设计了协同控制和管理方法，实现微电网间的协调优化，降低通信负担；文献[6]考虑多种类型负荷的接入问题，考虑到自身的功率需求、请求响应时间以及持续工作时间都存在随机性，设计了Markov控制的算法，实现微网长期运行成本最优；文献[7]建立了层级式微电网互联模型，通过优化系统经济性从而优化配置储能系统容量；文献[8]针对微电网群的优化运行，考虑运行指标为二次函数时的情况，通过使用分布式牛顿法和基于一致算法的信息传递设计了优化算法，实现更好的收敛速度，且对通信的要求低；文献[9]针对多微电网的配电网需求响应问题，通过在二次调度中应用博弈理论，提出基于源荷的交互式双层调度方案，实现配电网层负荷需求的优化；文献[10-12]针对含可再生分布式能源多微网使用粒子群经济优化策略，提高了新能源的利用率；文献[13]针对开放的市场环境，先给出了含多微电网的配电系统电能交易规则，并提出了开放市场环境下的多微电网系统双层调度方法，提高了微电网的收益；文献[14] 针对多个互联电网组成的多微网系统，提出基于分解-协调思想的递阶预测控制能量优化管理方法，实现多微网能量协调，提高新能源利用率，但所研究的多微电网系统仅含有传统能源和新能源，未包含储能装置，因此未考虑多微电网储能装置的动态特性，且其模型要求子微电网之间按照固定的比例系数进行电能交互，具有一定的保守性，其微电网系统的控制性能有待进一步进行改善和提升。

针对多微电网中微电网间存在能量流动和相互关联，具有系统维数高、关联复杂特点，通过使用大系统分解协调思想的关联平衡原理将多微电网整体优化的复杂的高维整体优化问题按照一定规律分解为若干个相互独立的低维子网优化问题，将原来集中的大规模计算分散到每个子网系统中进行，从而大幅度减小计算量，降低对单个控制器的计算性能要求；考虑到通常所采用的最速上升法或共轭梯度法在协调级寻优过程中迭代计算时间较长，进一步引入Barzilai-Borwein梯度法，有效提升协调级迭代计算寻优过程的收敛速度，对各子网系统的独立优化解进行协调，驱动各子网的独立优化解快速收敛至多微电网的整体优化解。随着时间推移，反复进行基于预测控制思想的滚动优化[15-17]，可以对多微电网优化调度取得理想的控制效果。

1 多微电网系统建模及优化问题描述

考虑由n个子微电网组成的多微电网系统结构如图1所示。多微电网系统中包含若干微电网，所有微电网都与同一条母线相连接。每个微电网内包含光伏或风机等新能源发电、燃气轮机或柴油发电机组等传统能源发电、蓄电池及用户负荷。微电网内由新能源发电及传统能源发电向用户负荷供电，每个微电网的蓄电池作为电能储能装置用于储存新能源多发的电能，并在负荷过高时向用户供电。微电网间可通过母线相互传输电能，协调不同微电网间的供电，进一步提高每个微电网对负荷供电的供电质量。每个微电网内均有各自的控制器，控制器负责优化每个微电网的各种供电形式使微电网内部的运行成本最小。各微电网间通过协调器协调微电网间的电能调度。

图1 多微电网系统结构Fig.1 Structure of multi-micro grid system

1.1 微电网内各部分的模型建立

对于第i(i=1,2,…,n)个微电网,该微电网内各设备单元的模型建立具体如下。

1.1.1 新能源供电

每个微电网内均有光伏发电、风力发电等清洁能源发电形式，考虑新能源供电发出的所有电量全部用于用户负荷供电或者蓄电池充电，没有弃风弃光。t时刻新能源发电功率记为Pn,i(t)，Pn,i(t)可通过预报技术较准确地预测得到。

新能源供电的运行维护成本fn,i(t)为

fn,i(t)=rn,iPn,i(t)

(1)

式(1)中：rn,i为新能源发电运行维护的成本系数。

1.1.2 传统能源供电

每个微电网内都装有微型燃气轮机或柴油发电机，微型燃气轮机及柴油发电机是使用化石能源的传统能源供电形式，存在化石能源储量日益枯竭、对环境污染大的缺点，在微电网运行中主要作用是在新能源供电及蓄电池供电均不能满足用户需求时作为辅助供电保证供电质量。

t时刻传统能源发电功率记为Pt,i(t)，由于实际中微型燃气轮机或柴油发机的发电出力均有上、下限，故Pt，i(t)满足机组出力约束：

Pt,i,min≤Pt,i(t)≤Pt,i,max

(2)

式(2)中：Pt,i,max和Pt,i,min分别为传统能源发电功率的上限和下限。

发电功率的爬坡率ΔPt,i(t)=Pt,i(t)-Pt,i(t-1)满足约束：

ΔPt,i,min≤ΔPt,i(t)≤ΔPt,i,max

(3)

式(3)中：ΔPt,i,max和ΔPt,i,min分别为传统能源发电功率爬坡率的上限和下限。

传统能源发电的运行成本主要包括燃料成本、运行维护成本及环保治理成本，综合考虑以上各种成本，传统能源发电的运行成本可以用二次函数表示，即传统能源发电的运行成本ft,i(t)为

(4)

式(4)中：ra,i为二次项成本系数；rb,i为一次项成本系数；rc,i常数项成本系数。

1.1.3 蓄电池

每个微电网内均装有蓄电池，在微电网内新能源发电供过于求时，蓄电池作为储能装置将多余的电能储存备用，在微电网内新能源发电供不应求时，蓄电池作为供能装置向用户负荷供电，降低微电网内部供电压力。

蓄电池荷电状态模型为

Si(t+1)=(1-δi)Si(t)+ηc,iPc,i(t)-

(5)

Si,min≤Si(t)≤Si,max

(6)

mc,i(t)Pc,i,min≤Pc,i(t)≤mc,i(t)Pc,i,max

(7)

md,i(t)Pd,i,min≤Pd,i(t)≤md,i(t)Pd,i,max

(8)

式中：Si(t)为蓄电池在t时刻的荷电状态；δi为蓄电池的自放电率；Pc,i(t)和Pd,i(t)分别为蓄电池在t时刻的充电和放电功率，ηc,i和ηd,i分别为蓄电池的充电和放电效率；逻辑变量mc,i(t)和md,i(t)分别为蓄电池在t时刻的充电和放电状态标志位；Si,max和Si,min分别为蓄电池荷电状态的上限和下限；Pc,i,max和Pc,i,min分别为蓄电池充电功率的上限和下限；Pd,i,max和Pd,i,min分别为蓄电池放电功率的上限和下限。

为保证每天的优化过程的连续性及蓄电池运行的经济性，强制要求蓄电池的荷电状态在每天的00：00时Si,0回到蓄电池初始荷电状态Si,set，即

Si,0≥Si,set

(9)

蓄电池的充放电的运行成本fs,i(t)为

fs,i(t)=rs,i[Pc,i(t)+Pd,i(t)]

(10)

式(10)中：rs,i为蓄电池充放电成本系数。

1.1.4 用户负荷

每个微电网内均有用电用户，t时刻用户负荷功率记为Pr,i(t)，Pr,i(t)可通过结合历史统计数据和需求预测技术准确地预测得到。

1.1.5 网间电能交换

各个微电网都连接在同一个母线上，t时刻微电网与母线间的电能交换功率记为Pe,i(t)，Pe,i(t)满足约束：

Pe,i,min≤Pe,i(t)≤Pe,i,max

(11)

式(11)中：Pe,i,max和Pe,i,min分别为微电网与母线间的电能交换功率的上限和下限。

微电网内部的电能传输满足能量守恒原则，即

Pc,i(t)-Pd,i(t)+Pr,i(t)=Pt,i(t)+Pn,i(t)+Pe,i(t)

(12)

各个微电网都连接在同一个母线上，任意一个微电网通过母线均可向其他所有微电网供电，也可通过母线从任意一个微电网取电。不具体考虑任两个微电网间的电能交换，只考虑每个微电网与母线间的电能交换，微电网间的电能交换通过母线自动分配，但总和满足能量守恒原则，即

(13)

1.2 优化问题描述

多微电网系统经济性能优化中主要考虑优化微电网内各部分的成本指标，即主要考虑新能源发电、传统能源发电及蓄电池充放电的运行维护及环保成本，由式(1)、式(4)、式(9)可知，在t时刻整个多微电网系统的成本函数为

(14)

多微电网系统经济性能优化以24 h为优化周期，取优化时域p=24，综合式(1)～式(13)可得多微电网优化调度问题可描述为

(15)

式(15)中：⨁表示“或”运算符号。

2 基于Barzilai-Borwein梯度法的多微电网系统递阶优化调度算法

该优化问题以互联的多微电网为研究对象，该对象需要优化的变量多，整体优化问题具有很高的系统维数；涉及地理范围广，微电网间的关联复杂；受天气、用户需求等不确定因素影响，多微电网中有很多不确定的变量；多微电网系统经济性优化不简单是单一目标的优化，涉及多微电网内各部分的经济性指标，需要在不同控制指标间相互平衡，目标具有多样性，是典型的动态大系统，通常会伴随产生较繁重的在线计算负担。采用递阶优化结构，利用大系统分解协调思想将复杂的高维多微电网整体优化问题按照一定规律分解为若干个相互独立的低维子问题，大幅度地减小计算量，且将原来集中的大规模计算分散到每个子网系统中进行，降低对单个控制器的计算性能要求；在协调级采用Barzilai-Borwein梯度法对各子网系统的独立优化解进行协调，提升协调级迭代计算寻优过程的收敛速度，驱动各子网系统的独立优化解快速收敛至多微电网的整体优化解。递阶优化结构如图2所示。

λ为协调因子图2 递阶优化Fig.2 Hierarchical optimization

2.1 基于空间分解的优化问题转化

分析上一节得到的多微电网优化调度问题[式(15)]可知约束可分为两类，一类是只涉及子微电网内部变量的约束：

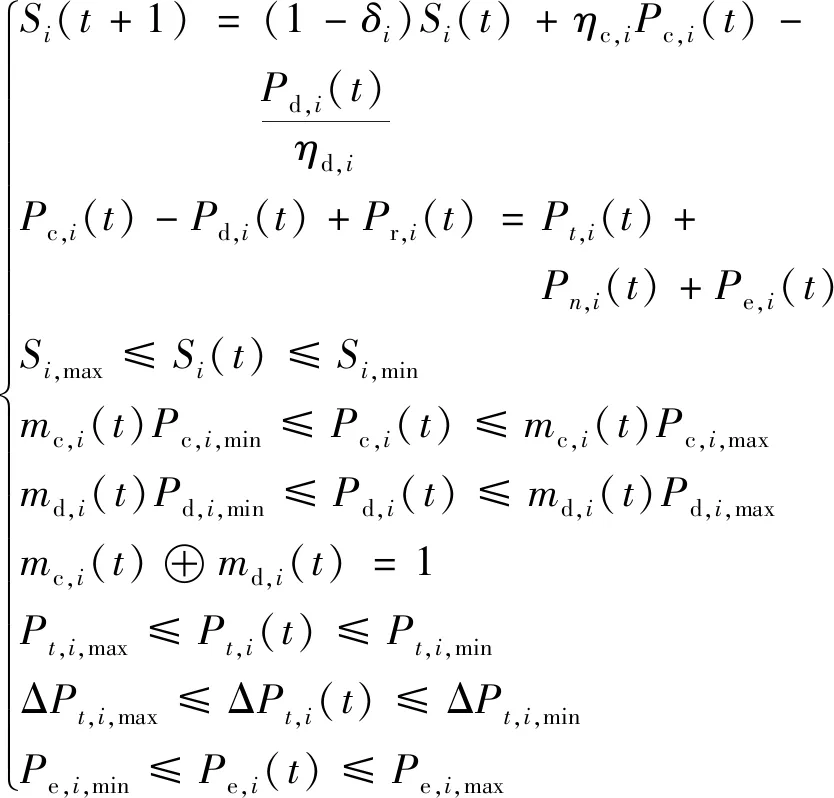
(16)

这一类约束包括蓄电池荷电状态模型、各变量的上下限约束及微电网内的能量平衡约束。

另一类式子微电网间的关联约束：

(17)

即微电网间能量流动的能量平衡约束。

针对子微电网间的关联约束[式(17)]，通过引入拉格朗日协调因子λt，t=1,2,…,24，把原优化问题的经济性能指标转化为对偶优化问题的经济性能指标：

(18)

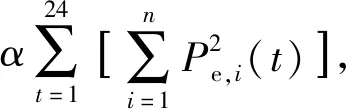
利用强对偶定理，可将原优化问题[式(15)]转化为极小极大问题：

(19)

将对偶优化问题的经济性能指标做如下整理：

(20)

由此可见对偶优化问题的指标按子系统可加性可以分离，第i个子微电网的经济性能指标为

(21)

由式(21)可见对偶优化问题的约束也按子系统可加性可以分离，则该对偶优化问题[式(19)]可拆分成每个子系统的优化问题。

(22)

分解后的子网优化问题可分别由各个子微电网内的控制器独立求解，且子问题的规模与整体优化问题相比有了很大的降低，对控制器的要求远低于集中控制。但由于各微电网独立求解的过程中没考虑其他微电网的供求，所求得的解不是多微电网系统的全局最优解，故需要设立一个协调器协调各微电网间的能量调度，即将原问题分解成两级迭代协调。

2.2 基于Barzilai-Borwein梯度法的多微电网系统递阶优化调度算法

对偶优化问题分解后可通过下述两级递阶优化算法按空间分两级求解。

第1级对于给定的协调因子λt(t=1,2,…24)，每个微电网i(i=1,2,…n)独立求解各自的子优化问题[式(22)]。该问题为混合整数二次规划问题，这里通过使用分支定界法求解。该级只进行每个子微电网的独立优化，随后将每个微电网优化得到的网间调度请求Pe,i发送给协调器。

第2级协调器的作用是通过更改协调因子λt使每个微电网的网间调度请求Pe,i满足式(13)。考虑到通常所采用的最速上升法或共轭梯度法在协调寻优过程迭代计算时间较长，因此引入Barzilai-Borwein梯度法以有效提升协调级迭代计算寻优过程的收敛速度，对各子网系统的独立优化解进一步进行协调，驱动各子网系统的独立优化解快速收敛至多微电网的整体优化解。即求解优化问题。

(23)

以得到最优的协调因子λt(t=1,2,…，24)。

记第m次迭代的解为

(24)

记φ(λ)的梯度为g，则第m次迭代φ(λ)的梯度g(m)为

g(m)=[

(25)

这里的Pe,i(t) (i=1,2,…,n；t=1,2,…,24)是第一级优化各微电网在协调因子在上一次迭代中得到的λ(m-1)的基础上求解各自优化问题得到的局部最优解。

定义s(m-1)=λ(m)-λ(m-1)，y(m-1)=g(m)-g(m-1)。

Barzilai-Borwein梯度法的求解步骤如下。

步骤1取初始解λ(0)，选取较小常数ε，0<ε<1，m=0。

步骤2每个微电网在拉格朗日协调因子取值为λ(m)下分别求解各自的子优化问题，得到每个微电网的独立最优解。

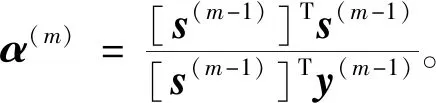
步骤5λ(m+1)=λ(m)-α(m)g(m)，m=m+1，转步骤2。

该级的计算主要进行于协调器内，协调器根据每个微电网独立优化得到的各自的网间调度请求迭代优化拉格朗日协调因子，并将新的协调因子下发给每个微电网。

该最优解为在当前预测得到的未来24 h的新能源发电及用户负荷下使多微电网系统整体的经济性指标最优的传统能源发电、蓄电池充放电及子微电网间电能调度的最优调度方案，由于实际中受天气、用户需求等不确定因素影响，每次优化用到的新能源发电及用户负荷预测值不尽相同，蓄电池蓄电量也不会跟预测值完全一致，为保证实际下发的调度指令能够及时响应新能源发电及用户负荷的变化，这里通过结合预测控制的滚动优化思想，每小时都在新的预测值下重复进行上述两级优化，只取每个优化变量的最优解序列的第一项作为实际控制量下发。

2.3 基于Barzilai-Borwein梯度法的多微电网系统递阶优化调度算法步骤

在上述两级空间分解协调基础上，综合预测控制的滚动优化思想和两级空间分解，给出基于Barzilai-Borwein梯度法的多微电网系统递阶优化调度算法。

步骤1起始时刻k=0时，初始化优化时域、迭代收敛精度、拉格朗日协调因子预估值。

步骤2k≥0时刻，检测蓄电池荷电状态信息，获取最新的新能源发电及用户负荷预测值。

步骤3按算法1所示过程执行Barzilai-Borwein算法，得到传统能源发电、蓄电池充放电及子微电网间电能调度的最优解。

步骤4取最优解第一项施加到各自的被控对象。

步骤5k=k+1，返回步骤2，重复以上步骤。

步骤6微电网间没有直接的数据交换，每个微电网与协调器之间也只交换每个微电网期望的网间调度电量和协调因子，每个微电网内其他所有变量均不需发送，本文算法可有效保护每个微电网的隐私。

3 数值仿真

多微电网系统结构如图1所示，其中每个微电网与母线间的联络线的功率约束取为Pe,i,min=-5 kW，Pe,i,max=5 kW，要求每天0时每个微电网的蓄电池初始荷电状态满足Si,0≥Si,set=60 kW·h。微电网内各设备的运行成本系数为：新能源发电运行维护的成本系数rn,i=0.5，传统能源供电二次项成本系数ra,i=10-3，一次项成本系数rb,i=1，常数项成本系数rc,i=5，蓄电池充放电成本系数rs,i=0.1。多微电网系统优化调度的优化时长为 24 h，时间间隔为15 min。

首先选取微电网个数n=6的多微电网系统进行仿真，分析本文算法的控制效果；随后，汇总和对比微电网个数为n=3、n=6及n=9时本文算法和集中式算法的优化用时及经济性指标，说明本文算法在降低求解计算量上的优势。

以微电网个数n=6组成的多微电网系统为对象进行仿真，其中每个微电网的机组容量配置如表1所示。多微电网系统24 h 内6个微电网各自的新能源发电出力及用户负荷的曲线如图3所示。

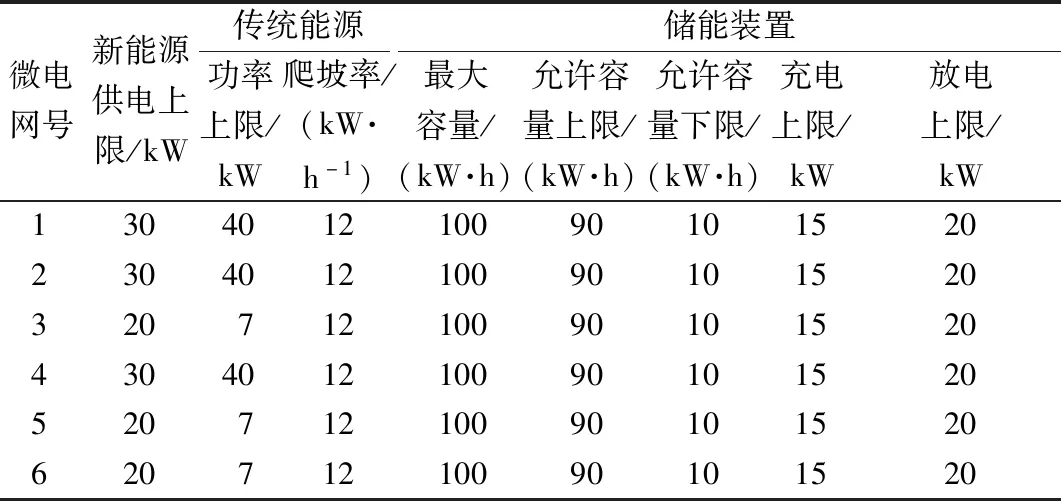
表1 机组容量配置Table 1 Unit capacity configuration

基于上述机组容量配置参数及24 h内电能供求数据，采用多微电网系统优化调度算法，其优化的调度结果如图4～图7所示。图4为在24 h内6个微电网的蓄电池荷电状态及充放电功率的仿真曲线图，其中蓄电池充放电功率取正值时表示向蓄电池充电，取负值时表示蓄电池向负荷供电；图5显示了每个微电网与母线间的电能交换数据，数据取正值时表示电能由母线流入微电网，数据取负值时表示电能由微电网流入母线；图6显示了每个微电网的传统能源发电数据。由图3知微电网3在4～15 h区间段、微电网5在0～8 h和21～24 h区间段、微电网6在12～23 h区间段，新能源发电均高于各自的用户负荷需求，从图4、图5可以看出，此时多余的电能一方面通过母线输送至其他微电网，另一方面向每个微电网内的蓄电池充电；另外，以微电网3为例，其在17 h后新能源完全不发电，而微电网3配备的传统能源供电又远不能满足负荷要求，此时优化算法调度微电网3传统能源发电(图6)，同时由蓄电池提供一部分供电，将在白天新能源发电供应充足时储存下的电能在供电存在缺口时输出，减小供电压力，实现削峰填谷(图4)，余下的用电缺口则通过母线向其他电量富裕的微电网借电(图5)，从而弥补用电缺口，实现微电网的供电量和用户负荷之间的有效平衡。

图3 各微电网的新能源发电出力及用户负荷曲线Fig.3 New energy power generation output and user load curve in microgrids

图4 微电网蓄电池调度Fig.4 Battery dispatching in microgrids

图5 微电网与母线间交换功率Fig.5 Exchanging power between microgrids and bus

图6 微电网传统能源发电功率Fig.6 Traditional energy generation power of microgrids

图7 微电网新能源发电出力Fig.7 New energy power generation output in microgrids

本文算法的求解时间及经济性能两个指标与集中式优化算法的对比详见表2中6个微电网情形下的相应数据。由表2可知，本文算法取得了与集中式优化算法相接近的系统性能。本文算法通过空间分解将多微电网这一高维系统的整体优化问题转化为各微电网低维子优化问题，有效降低了优化求解时间，表2中的求解时间数据对比也验证了本文算法在计算效率上的有效性。

为了进一步说明本文算法相比集中式优化算法在求解时间上的优势，进一步分别增加3个和9个微电网时的优化调度仿真。汇总3个、6个和9个微电网三种情况下本文算法和集中式算法的求解时间及经济性指标如表2所示。从表2可以看出，在3、6、9个微电网情况下，本文算法取得了与集中式算法相接近的系统性能。在计算效率方面，当微电网个数是6和9时，本文算法的求解时间分别是21.4、43.5 s，而集中式优化算法的求解时间分别达到266.5、1 641.4 s，可以看出本文算法在求解时间上有着较大优势，且随着微电网个数增加，本文算法在求解时间上的优势更加显著。综上可知，当多微电网系统维数规模较大时，本文算法能够有效降低多微电网优化问题求解时间，从而提高计算效率。

表2 优化时间和经济性能结果对比表Table 2 Comparison of optimization time and economic performance results

4 结论

针对多微电网系统能量管理的优化调度问题，通过关联平衡原理设计了基于Barzilai-Borwein梯度法的递阶优化算法，在多微电网优化的计算效率、系统性能和系统运行安全性方面取得了较优的控制效果。

(1)对含有储能装置动态特性的多微电网系统进行空间分解，在此基础上对微电网子系统进行优化，进而采用Barzilai-Borwein梯度法在子微电网之间进行协调，提升了协调级迭代计算寻优过程的收敛速度，高效实现了多微电网系统的能量优化管理。仿真结果表明本文方法以较低的计算量取得了良好的多微电网能量管理效果。

(2)空间分解后微电网间不存在直接的信息交换，可有效保护各个微电网的隐私；空间分解将整体优化问题大规模的计算量分解到每个微电网内进行，即使因故障问题导致某个微电网与协调器切断了通信，也能够独立优化运行，提升了整个系统运行的稳定性和安全性。