感应电机驱动系统的新型PDTC设计

李玉丹,王松涛,巴文兰

(1.郑州理工职业学院 机电工程系，郑州 451150；2.施耐德电气有限公司，郑州 450000；3.河南工业大学 机电工程学院，郑州 450001)

0 引 言

近年来，随着电力电子技术、集成电路技术和数字芯片的发展，电机驱动控制系统的控制策略趋于算法更复杂和性能更优良[1]。目前主要的电机驱动控制方案包括磁场定向控制[2-3]、直接转矩控制(Direct Torque Control，DTC)[4-5]和模型预测控制[6-7]。其中DTC首次于1985年提出[8]，其不同磁场定向控制，无需坐标变换即可直接控制输出转矩，易于实现且动态响应快，但存在转矩脉动和可变开关频率的问题[9-11]。预测控制技术提出稍晚于DTC，但近年来受到研究人员的高度重视[12-13]。预测控制基于离散时间域模型对变量的未来状态进行预测，并经由预设的成本函数直接计算和选择最优开关状态进行输出以实现电机驱动。预测控制能有效提高对外部干扰的不敏感度，故成功应用于各类电机驱动器中[14-15]。

有学者提出将DTC与预测控制相结合以形成高性能控制方案的思路，称为预测直接转矩控制(Predictive Direct Torque Control，PDTC)[16-23]。文献[16]中将模型预测控制结合直接转矩控制扇区划分原理进行开关磁阻电机的换相设计从而优化了电机输出转矩的脉动，但局限于开关磁阻电机。文献[17]针对双三相永磁同步电机引入PDTC方案以降低DTC中开关表计算量大的问题，实现了解耦控制，但依然存在对象局限的问题。文献[18]率先将PDTC应用于感应电机驱动控制，但控制器中认为负载转矩是已知扰动，故控制效果不理想，转矩脉动较高。文献[19]基于状态空间模型开发了PDTC，但文献[20]指出其离散时间域模型精确度不高。文献[21]中提出了由三电平逆变器驱动的感应电机PDTC算法，其算法能在每个采样周期中选择合适的开关序列，并在成本函数中考虑了中点电位平衡控制，但输出转矩脉动抑制的权重系数不高，转矩脉动较大。文献[22]针对降低系统损耗设计了低损耗PDTC用于感应电机控制，但局限于仿真研究，无实际实验数据。文献[23]针对矩阵变换器驱动感应电机设计了专门的PDTC算法，可降低系统共模电压，并提高驱动效率。

由上述文献研究基础，本文设计了新型PDTC方案用于驱动感应电机。PDTC中引入了卡尔曼滤波器(Kalman Filter，KF)[24-25]对磁链进行估计，并将预测转速控制器和负载转矩观测器相结合来进行转速参考值跟踪和干扰抑制。PDTC中设计了成本函数算法可处理系统非线性和各种约束以选择使得转矩和定子磁链误差最小的开关序列在下一个采样周期中应用。最后，对新型PDTC的效果进行了对比实验验证。

1 感应电机数学模型

感应电机数学模型为：

(1)

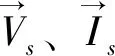
(2)

其中,p是极对数。对应到αβ分量，(1)式可改写为

(3)

系统输出为定子电流，可表示如下：

(4)

2 新型PDTC方案设计

图1为新型PDTC方案框图。

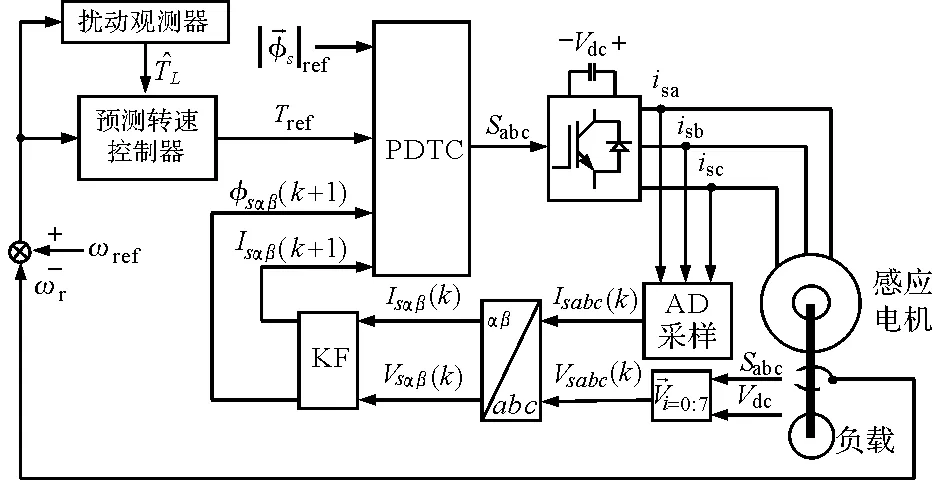
图1 新型PDTC方案框图

2.1 PDTC设计

图1所示，预测控制器取代了传统DTC中的滞环比较器和开关选择表，进一步结合KF实现了精准的磁链估计和负载转矩观测。使用测得的直流侧电压Vdc和逆变器开关状态Sa、Sb和Sc，可得到每个采样周期的定子电压表达式：

(5)

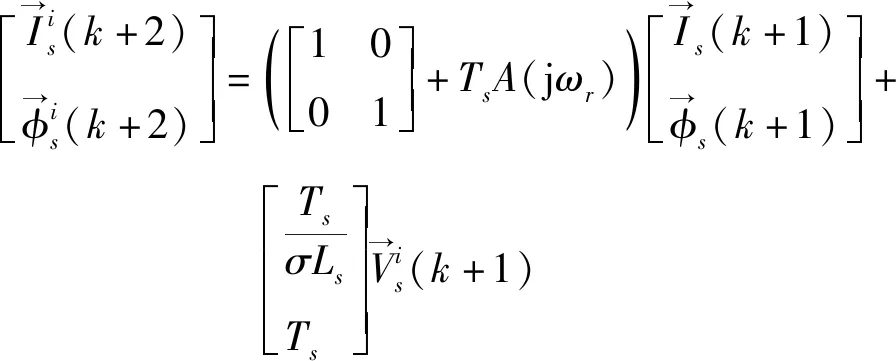
其中,Ts为采样周期，上标“i”代表i=0∶7，即对8个定子电压矢量进行遍历，故上式的计算结果将出现8组。将结果代入定义如下的成本函数Fc计算。

(7)

表1 开关状态表

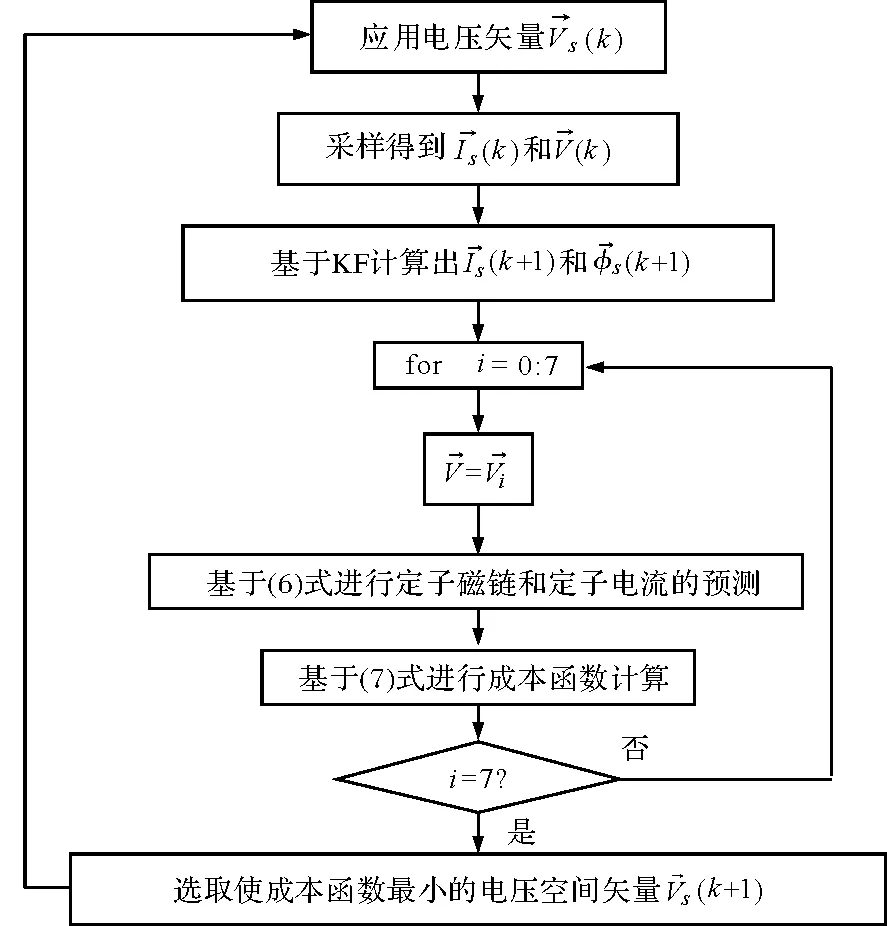
图2 PDTC算法流程图

2.2 KF设计

KF作为一种状态估计器可基于系统状态空间描述，对系统输出和输入进行数据观测以求取难以测量的系统状态的最优估计值[24-25]。考虑到状态和测量噪声，用于估算定子磁链的离散时间域电机模型如下所示：

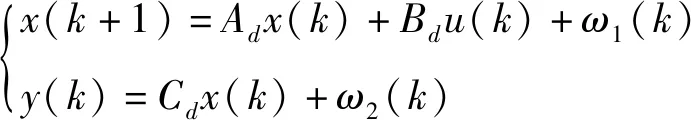
(8)

其中ω1和ω2分别为过程和测量噪声随机矢量。预测和校正步骤设计为：

(9)

(10)

P(k+1|k)=F(k)P(k|k)FT(k)+Q

(11)

(12)

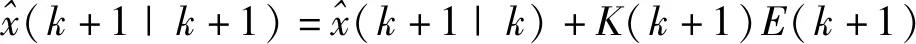
(13)

(14)

P(k+1|k+1)=P(k+1|k)
-K(k+1)H(k+1)P(k+1|k)

(15)

(16)

其中Q、R和K分别为状态矩阵、测量协方差矩阵和卡尔曼增益矩阵。

2.3 预测转速控制器设计

预测转速控制器的主要目的是为PDTC提供转矩参考。

感应电机的转子动力学方程为：

(17)

其中,Te和TL分别为电磁转矩和负载转矩，J和B分别为转动惯量和摩擦系数。Te和TL分别可视为控制变量和未知扰动，转子转速ωr为输出量。预测算法设计中允许转速跟踪误差eω在一个预测范围T内达到零，即：

eω=ωr(t+T)-ωref(t+T)=0

(18)

其中,ωr(t+T)和ωref(t+T)分别为预测范围T内的实际转速和参考转速。ωr(t+T)由泰勒级数展开后可写为：

(19)

类似地，ωref(t+T)可表示为：

(20)

因此，最优控制由下式给出。

(21)

将上式代入式(17)，并结合式(18)、(19)和(20)，可得到 的动态为：

(22)

由上式可知，预测时间应选得尽可能短以确保良好的动态性能，但这种选择可能会导致动态电流超过极限值，尤其是较大的阶跃变化动态时，为了避免这个问题，需设置较为平稳变化的转速参考。

进一步，将式(17)重写为如下形式：

(23)

定义负载转矩观测器如下：

(24)

其中,p0是观测器设置常数。转矩估计误差及其动态描述为：

(25)

(26)

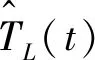
(27)

将上式代入式(24)可得：

(28)

设eω(0)=0，对上式进行积分，可得：

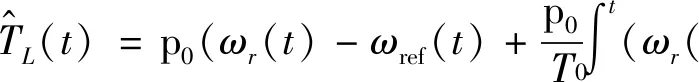
(29)

上式代表负载转矩观测器的特性与转速PI控制器类似。其可以补偿未知扰动，并改善转速参考值跟踪性能。根据式(26)，负载转矩观测器的收敛速率取决于p0/J，故需将其选择为一个较大值从而确保快速抑制干扰，但考虑到较大的观测器增益可能会放大测量噪声，故需进行权衡设计。

3 实验验证

为验证新型PDTC控制方案的效果，搭建了感应电机与永磁直流发电机对拖的测试平台，感应电机主要参数如表2所示。同时，基于IGBT构建了逆变器主体，控制算法则由基于FPGA的实时仿真系统工作站完成，该工作站运行带有Xilinx公司System Generator支持的实时代码生成器，因而预先在Matlab/Simulink中开发设计算法并整定控制参数，仿真完成后即可直接生成比特流下载文件进行实际测试。实际实验中将KF、PDTC和预测转速控制器的采样周期均分别设置为30 μs、30 μs和90 μs，预测范围T设置为4.5 ms。

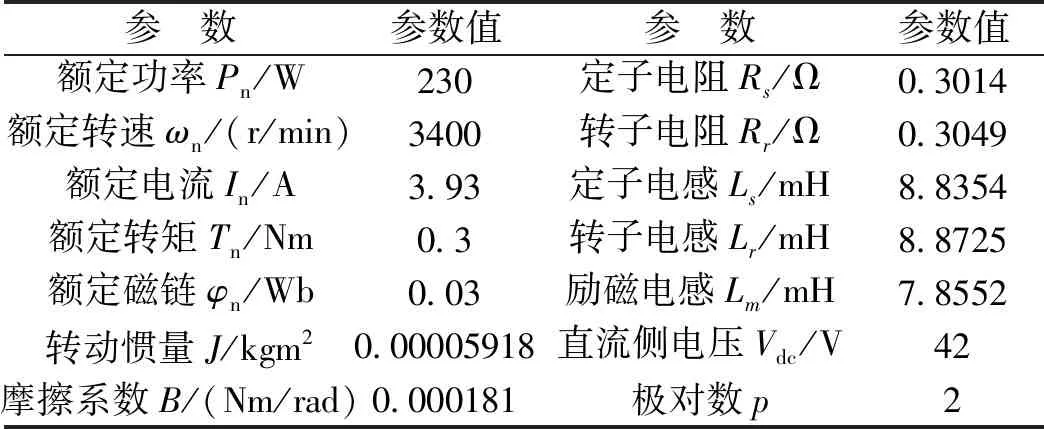
表2 感应电机参数

首先，进行了感应电机的正转和反转测试，在t=1.25 s时，电机被加速至2000 r/min，然后进行反转驱动，在t=2.75 s时，转速被控制为-2000 r/min，此后进一步控制转速在t=4 s时达到1000 r/min，最后将其减速至0 r/min。PDTC控制方案的优势通过与传统DTC方案的对比实验验证。图3和图4分别为两种方案下的实验波形。对比图3(a)和图4(a)，图3(b)和图4(b)中转速和转矩波形可得：两种控制方案的转速参考值跟踪和转矩估计均非常准确，且动态响应也很快速，但新型PDTC方案的转矩脉动更小。从图3(c)和图4(c)中磁链波形可发现，两种控制方案下的估计磁链和实际磁链均吻合，验证了KF估计磁链具有精确度较高的优点。对比图3(d)和图4(d)中的定子电流波形还可看出，新型PDTC方案作用下的定子电流纹波更小，这和转矩脉动减小是相互呼应的。图3(e)、图3(f)、图4(e)和图4(f)为两种方案下的定子电流波形细节及其THD分析，新型PDTC方案与传统DTC相比，将定子电流的THD从11.93%降低至5.76%。双向转速测试结果验证了新型PDTC在保留DTC控制方案的快速响应优势下能有效降低转矩脉动和定子电流纹波。

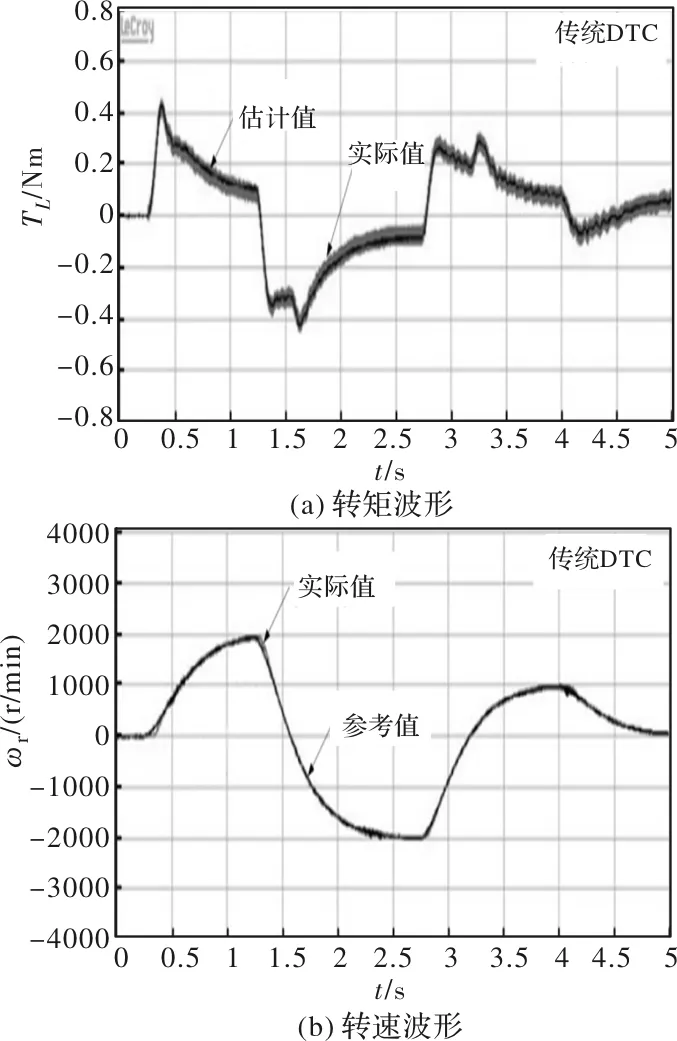
图3 双向转速测试波形(传统DTC)

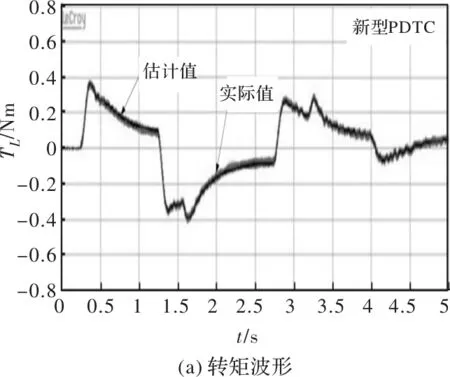
图4 双向转速测试波形(新型PDTC)

进一步，对所提出的PDTC方案的抗扰能力和鲁棒性进行了实验测试。控制电机空载运行，转速为1500 r/min，在t=2.2 s和t=4.4 s两个时间点突加负载转矩，同时参考转速保持恒定为1500 r/min。图5所示为测试结果。从图中可看出，新型PDTC控制器作用下的稳态误差可以快速消除，并实现了精确的转速参考值跟踪。

图5 突加负载转矩测试波形

4 结论与展望

本文设计了一种新的PDTC方案以克服传统DTC方案中转矩脉动大的问题。新型PDTC方案中引入KF完成了对磁链的精确估计并降低了测量噪声，实现了转速的鲁棒调节。同时，负载转矩观测器可提高干扰抑制能力。新的PDTC方案还使用了两步预测算法来补偿延迟。对比实验结果证明，PDTC保留

了传统DTC控制方案的快速动态响应特性，同时还有效降低了定子电流纹波和转矩脉动，故整体性能较优。进一步需研究的方向是如何优化新型PDTC方案的计算量，以提高工程应用适用性。