永磁同步电机无权值全速域模型预测磁链控制

霍 闯，於 锋，茅靖峰

(南通大学 电气工程学院，江苏 南通 226019)

0 引 言

永磁同步电动机(Permanent Magnet Synchronous Motor, PMSM)具有损耗小、起动力矩高、起动时间较短、过载能力高等优势[1]。传统的永磁同步电机控制方法主要有矢量控制(Vector Control, VC)和直接转矩控制(Direct Torque Control, DTC)[2]。VC是一种通过控制励磁电流和转矩电流来控制磁链和转矩的一种线性控制方法。但是坐标变换复杂，且电流调节器通常为具有滞后作用的PI控制，使得系统动态性能差。虽然DTC通过滞环控制器与离线开关表能够简化系统的运算，但存在开关频率变化大，低速时电机性能差的缺陷[3-5]。随着微处理器性能的提升，模型预测控制(Model Predictive Control, MPC)的关注度也得到提升。MPC通过预测下一时刻系统状态的变化趋势，并利用滚动优化来选取当前时刻相应的最优控制动作，从而实现对目标的精确控制[6]。因此一种源于DTC的模型预测转矩控制(Model Predictive Torque Control, MPTC)方法被提出。MPTC通过系统的预测模型直接对转矩和磁链进行预测，并通过相应的价值函数选择最优电压矢量，具有结构简单、动态响应快等优点[7-8]。

然而MPTC的目标函数中存在转矩、磁链等量纲不同的控制变量，因此，需要设计相应的权值系数来实现对多个变量的同时控制。文献[9-10]提出了全速域模型预测控制，在恒转矩区和恒功率区通过在线优化完成价值函数的确定。文献[11]提出了一种基于最大转矩电流比控制的PMSM转矩预测控制方法。在推导MTPA控制原理的基础上，分析了转矩预测的控制机理及性能指标函数。上述文献中提及的方法都有转矩脉动大的缺点，为解决这一缺点，文献[12]提出了基于占空比控制的双矢量模型预测转矩控制，利用价值函数选择出最优电压矢量与零矢量共同作用，基于占空比控制分配矢量作用时间，很好地改善了电机性能。文献[13]也分析了传统感应电机直接转矩控制的转矩脉动及磁链轨迹，并且提出一种预测控制算法与占空比控制技术相结合的新型控制方法改善系统性能。但是两种方法中权值系数设计复杂，并且无相关理论支持。

针对价值函数中权值系数设计复杂，转矩脉动大的问题，本文提出了一种适用于全速域的永磁同步电机模型预测磁链控制(Model predictive flux control, MPFC)。MPFC将定子磁链和电磁转矩的控制转换为等效的定子磁链矢量的控制，从而完成权值系数的消除。在此基础上，通过q轴磁链无差拍计算占空比，完成双矢量模型预测磁链控制。进一步地，从最大转矩电流比控制以及弱磁控制的基本理论出发，设计了全速域价值函数，实现了PMSM的全速域控制。最后，仿真和实验结果证明了所提方案在基速以下时转矩脉动较小，并且电机全速域运行时具有较高的动态响应性能。

1 PMSM数学模型

本文研究对象为内埋式永磁同步电机(Interior Permanent Magnet Synchronous Motor, IPMSM)。d-q坐标系下的数学模型如下：

定子磁链方程：

(1)

电压方程：

(2)

电磁转矩方程：

(3)

其中，id，iq和ud，uq分别为直、交轴电流和电压；Ld、Lq为直、交轴电感；ψsd、ψsq为定子磁链直、交轴分量；ωr为转子电角速度；δ为定子磁链与d轴夹角；ψf为永磁体磁链；Rs为定子每相电阻；np为极对数；Te为电磁转矩。

2 模型预测磁链控制

2.1 单矢量模型预测磁链控制

将式(1)代入式(2)，可得永磁同步电机定子电流瞬时方程为：

(4)

利用一阶欧拉式(5)将IPMSM电流微分方程式(4)离散化，求得电流预测模型为式(6)。

(5)

(6)

其中，Ts为系统的采样周期；id(k)、iq(k)为k时刻定子电流在d-q轴分量上的电流测量值；id(k+1)、iq(k+1)为k+1时刻定子电流在d-q轴分量上的电流预测值；ud(k)、uq(k)为k时刻定子电压在d-q轴分量上的电压。

将公式(6)代入公式(1)可得定子磁链预测方程：

(7)

其中，ψsd(k+1)、ψsq(k+1)为k+1时刻定子磁链在d-q轴分量上的磁链预测值。

将式(1)代入式(3)并且对δ进行求导，整理得到k+1时刻负载角参考值公式(8)，求得磁链预测参考模型为式(9)：

(8)

(9)

2.2 双矢量模型预测磁链控制

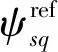
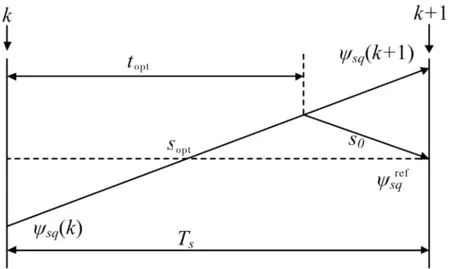
图1 占空比计算示意图

(10)

其中，topt为最优开关矢量作用时间；Sopt为最优开关矢量作用时ψsq的斜率；S0为零矢量作用时ψsq的斜率。

由式(1)和式(2)可以推得：

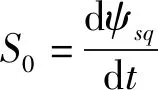
(11)

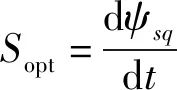
(12)

将式(11)和式(12)代入式(10)中可得最优矢量作用时间为：

(13)

3 全速域控制

3.1 最大转矩电流比控制

当电机转速为基速以下时，铁损比铜损小很多，为了利用磁阻转矩，采用MTPA控制策略。对于同一负载转矩，MTPA控制所需的定子电流更小，有更高的电流利用率，同时能够提高系统恒转矩区运行速度带宽和系统效率。

此时，定子磁链ψs满足关系式：

(14)

将式(14)和式(1)代入式(3)，并对δ求导可得：

(15)

在恒转矩区，电磁转矩Te为定值，令式(15)为0，此时定子电流为最小值，则有：

(16)

图2为MTPA的数学意义。由式(16)可知，MTPA的运行轨迹本质上是一个以式(17)为对称轴的双曲线。

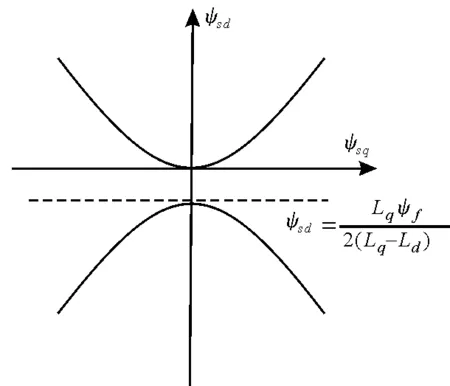
图2 MTPA数学意义

(17)

本文应用MTPA控制策略，价值函数包括：

(1) 磁链跟踪。为减小调节过程中的误差，跟踪函数设计为

(18)

(2) MTPA区域收敛。根据式(16)MTPA轨迹，可得MTPA收敛函数为式(19)。要使定子磁链处在MTPA轨迹上，需控制该函数无限接近于0。

(19)

(3) 约束条件。定子磁链受到电机给定磁链ψf的限制，因此，磁链限制条件设计为

(20)

图2所示的两条曲线满足式(16)，但上侧轨迹产生的电磁转矩大于下侧，所以定义方向选择函数：

(21)

3.2 弱磁控制

当电机速度达到基速时，电磁转矩减小，反电动势接近额定电压最大值，所以要通过弱化气隙磁链的方法，拓宽电机的调速范围。

考虑定子电压us受到最大值usmax的限制，则有：

(22)

电机高速时电阻远小于电抗，忽略定子电阻压降，将式(1)、式(2)与式(22)联立，可得电机高速运行时的定子电压us为：

(23)

可以看出，电压轨迹为d-q坐标系中的一个圆。永磁同步电机稳定运行时定子电流受到最大定子电流Imax的约束，则有：

(24)

当电机运行于基速以上时，为了防止电机运行失步，采用最小磁链转矩比控制方式[14]。将式(3)与式(19)联立，并对ψsd求导可得：

(25)

其中，ψs为定子磁链。

再令式(25)为零，可得最小磁链转矩比轨迹方程为：

(26)

对于弱磁控制的价值函数，控制要求主要有：

(1)跟踪IPMSM的磁链，跟踪函数与式(18)相同。

(2)弱磁区域收敛。弱磁区域收敛标准为：

(27)

其中，Vdc为直流母线电压；λm为电压系数。

(3)约束条件。IPMSM在弱磁区域运行时，受到逆变器的最大输出电压限制，则有：

(28)

(29)

其中，η为限制条件中间变量。

电机弱磁区域运行时需满足式(23)，则有：

ζ=[(ψsd(k+1))2-ψf·ψsd(k+1)-(ψsq(k+1))2]·
(Ld-Lq)+ψf·[ψsd(k+1)-(ψsq(k+1))2]

(30)

(31)

其中，ζ为电机高速稳定运行条件中间变量。

在转矩输出相同时，最小磁链转矩比能够进一步提高IPMSM的转速范围。

4 全速域价值函数

价值函数中包括磁链跟踪、区域收敛以及约束条件，因此：

g=gF+gc+gL

(32)

当电机转速低于基速时，gc=gMTPA且gL=gFMAX+gdir；当电机转速高于基速时，gc=gFW且gL=gFMAX+gumax+gstab。

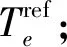
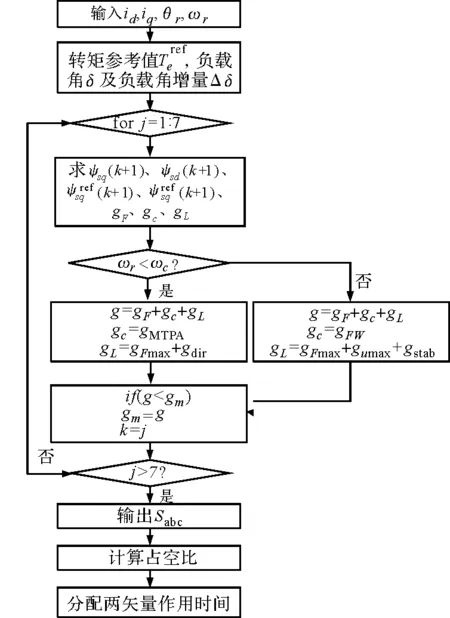
图3 全速域控制流程图

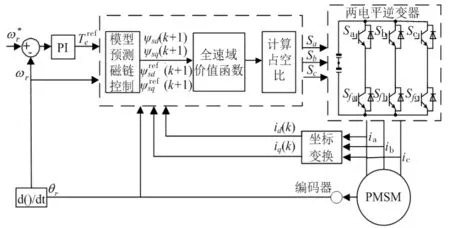
图4 全速域结构框图

5 仿真结果及分析

在Matlab/Simulink仿真环境中对图4所示的全速域MPFC策略进行仿真验证，并对仿真结果进行对比。IPMSM参数见表1。

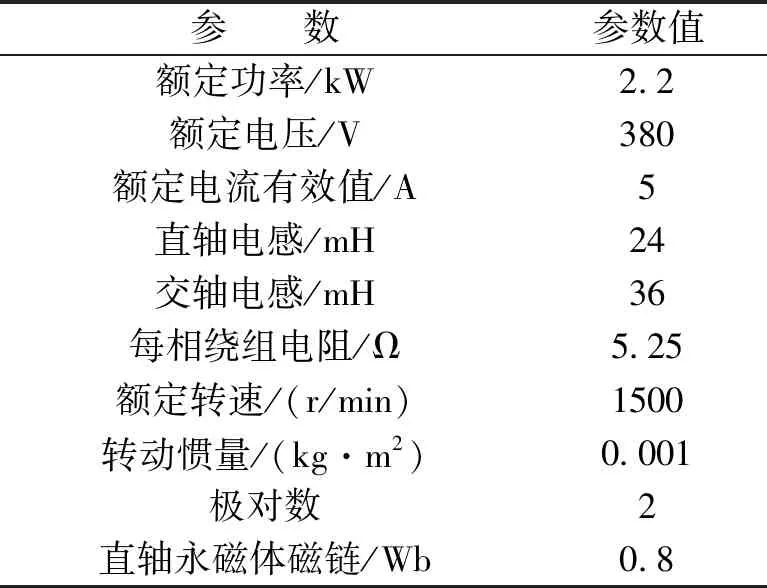
表1 IPMSM参数

5.1 基速以下单双矢量稳态仿真对比

验证基速以下基于单双矢量最大转矩电流比控制对比时，在给定转速400 r/min，电磁转矩4 Nm的条件下进行仿真验证。如图5所示为单双矢量稳态对比，此时图5(a)单矢量的转矩脉动为33%，而图5(b)双矢量的转矩脉动只有20%；对比两种方案的电流THD，单矢量电流THD为17.49%，而双矢量电流THD为7.96%。通过对两种方案的比较可以看出双矢量MPFC的稳态性能更好。

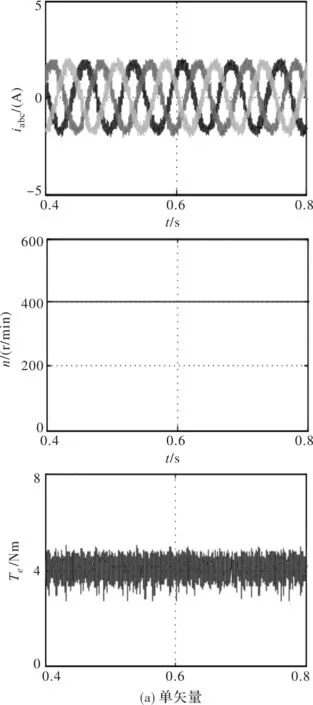
图5 单双矢量稳态波形

5.2 全速域模型预测磁链控制仿真

为分析全速域模型预测磁链控制的动态性能，仿真工况设置为：电机由空载起动到达1800 r/min，在t=0.4 s时突降转速至0 r/min。如图6所示为全速域电流、转矩及转速仿真波形，图6(a)为定子电流is及d-q轴分量id、iq波形图，图6(b)为电机转速图，电机起动5 ms后到达给定转速，当给定转速在t=0.4 s时变为0 r/min时，电机转速10 ms后变为0 r/min，同时定子电流产生较大的超调以迅速响应转速的变化；图6(c)为电机全速域运行时三相电流波形图，图6(d)为电机电磁转矩波形图。电机起动阶段采用最大转矩电流比控制，5 ms内三相电流达到10 A，转矩达到9 Nm，而后电机转速稳定在1800 r/min，三相电流值为4 A，t=0.4 s时转速突降至0 r/min，此时电流及转矩7 ms后再次到达最大值。通过上述分析可以看出全速域模型预测磁链控制的动态性能良好。

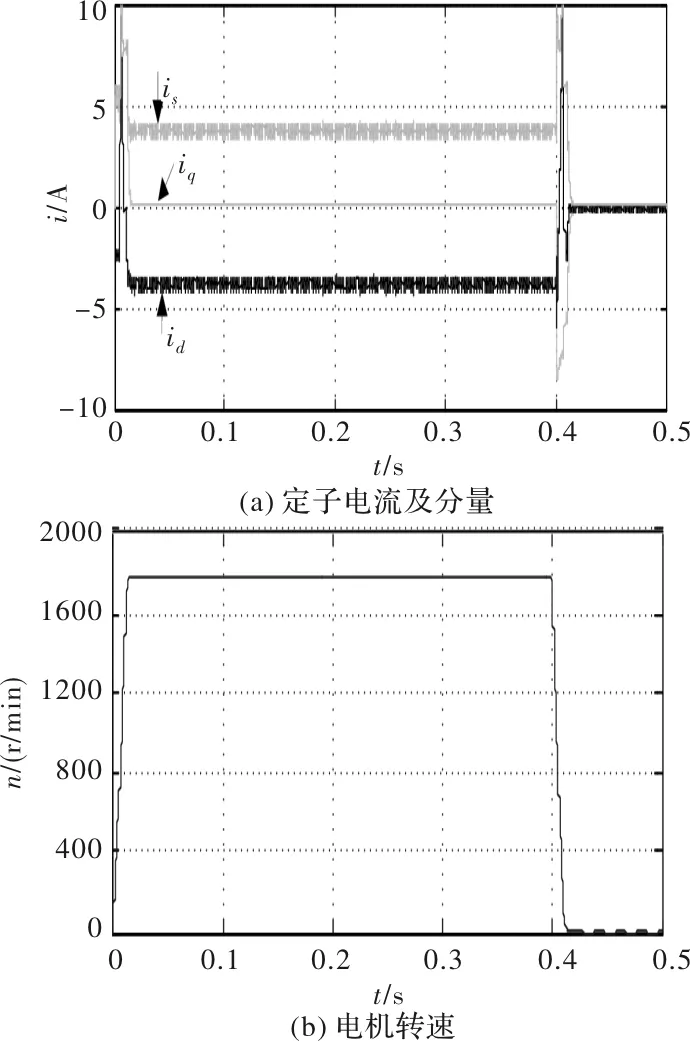
图6 全速域电流、转矩及转速波形

6 实 验

为进一步验证理论分析的正确性，本文对一台额定功率为2.2 kW的三相PMSM进行了实验研究，实验平台如图7所示。实验平台处理器采用dSPACE1104，并与Matlab/Simulink2009a的仿真平台进行连接，通过在Matlab软件下编译仿真，产生程序代码，进而建立各项参数可在线调节的实验系统。电机参数见表1，实验中单双矢量的采样频率设置为5 kHz。

图7 实验平台

为比较基速以下基于单矢量MTPA和本文所提出的基于双矢量MTPA的稳态性能，对于这两种控制策略，给定转速300 r/min，给定负载4 Nm，进行实验验证。通过对图8(a)单矢量和图8(b)双矢量MPFC比较可以看出双矢量MPFC转矩脉动更小，电流谐波含量更少。

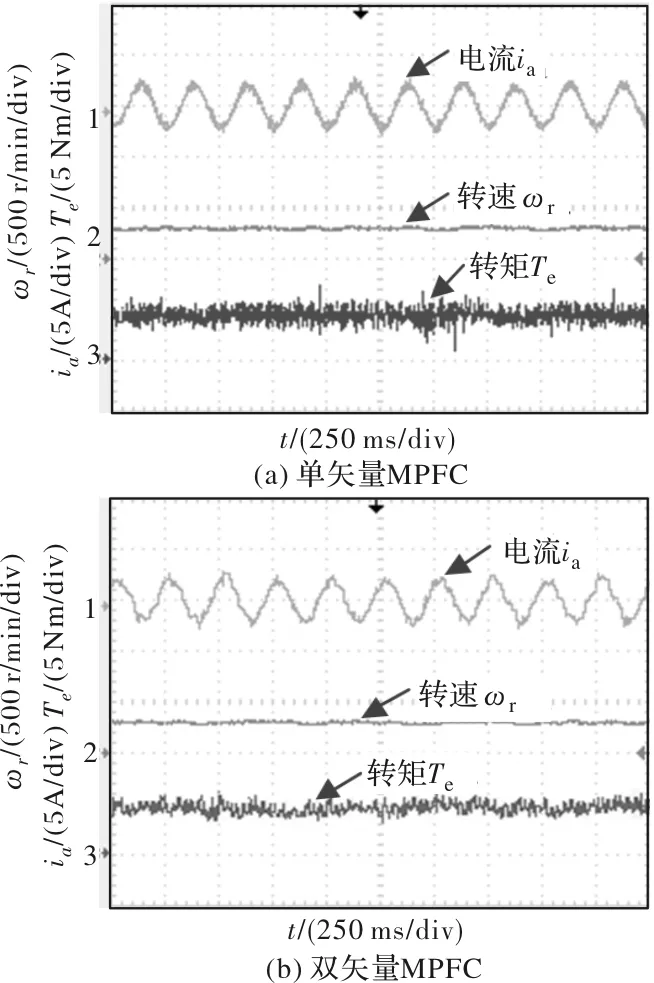
图8 单双矢量稳态性能分析

为了分析两种控制方案的动态性能，在图9中，给定转速400 r/mim，初始负载4 Nm，运行一段时间后负载突变到6 Nm，对于图9(a)单矢量MPFC和图9(b)双矢量MPFC两种控制策略，转矩均在125 ms内达到6 Nm，转速基本保持不变。在图10中，给定负载4 Nm，初始转速200 r/min，运行一段时间后转速突变到400 r/min，此时图10(a)和图10(b)两种控制策略下的转速均在100 ms内达到给定转速，转速几乎无超调。通过对图9和图10的分析可以看出单双矢量模型预测磁链控制具有基本一致的快速动态响应。

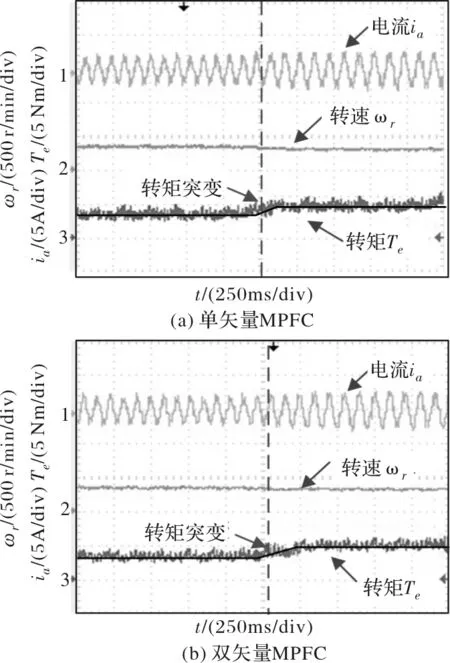
图9 转矩突变条件下实验性能分析

图10 转速突变条件下实验性能分析

7 结 语

在电机运行时，为了消除预测转矩控制中权值系数，并且减小转矩脉动，本文提出了一种永磁同步电机无权值全速域模型预测磁链控制方法。首先建立PMSM数学模型，并且详细论述了基于MPFC的MTPA策略和弱磁控制策略，并且在基速以下时加入基于占空比控制的双矢量MPFC策略，而后对该方法的稳态和动态性能进行了仿真与实验验证。电机基速以下运行时，基于占空比控制的MPFC不仅具有较高的动态响应性能，同时有效降低了转矩脉动与电流谐波含量；系统高速时也能获得较好的动稳态性能。仿真和实验结果证明了所提方案在基速以下时转矩脉动较小，并且电机全速域运行时具有较高的动态响应性能。