改进免疫遗传算法求解柔性作业车间调度问题

曹坤煜，陈永当，宋辛辛，强冰冰

(1.西安工程大学 机电工程学院，陕西 西安 710600； 2.西安市现代智能纺织装备重点实验室，陕西 西安 710600； 3.昆明理工大学 机电工程学院，云南 昆明 650500)

0 引 言

调度是企业智能化生产管理提高效率与效益的重要抓手。柔性作业车间调度(flexible job-shop scheduling problem，FJSP)，因其能够根据产品的制造需求快速响应市场变化，合理配置有限的制造资源，更符合实际生产需求而被广泛应用。但在运用过程中也会出现复杂性、动态模糊性、多约束性等特点，属于典型的NP-Hard问题[1]。因此对其研究具有重要的学术意义和应用价值。

近年来，随着企业市场化进程的不断推进，FJSP问题以成为学术界研究的热门课题。国内外学者已经相继提出了多种求解FJSP问题的有效算法。如：王春等[2]针对多目标动态柔性作业车间调度问题，通过引入虚拟工序和虚拟工时概念，提出了一种改进的遗传算法。Liu X等[3]通过使用候选操作机制构建了机器的调度方案，提出了一种基于蚁群优化(ACO)的集成过程计划与调度优化算法。李浩等[4]为了使算法跳出局部最优快速达到全局最优，提高算法的收敛性，提出了一种自适应变参粒子群算法。Li X等[5]针对FJSP问题提出了一种遗传算法与禁忌搜索算法相结合的混合策略，并通过与其他算法横向测评验证了混合算法的有效性。刘洪铭等[6]提出了自适应权重混沌的粒子群优化算法，通过引入莱维飞行、变邻域搜索、混沌，增强了算法的搜索能力。Gao等[7]针对具有模糊处理时间的车间调度问题，通过设计启发式规则来初始化种群，提出了一种改进的人工蜂群(IABC)算法。杨振泰等[8]考虑遗传算法中染色体编码的特殊性，提出了融合Powell搜索法的遗传算法。田旻等[9]为弥补遗传算法局部搜索能力的不足，提出了考虑传输时间的粒子群遗传混合算法。Qin W等[10]通过引入到期日期偏差的概念，设计了滚动视距驱动策略，提出了一种基于蚁群算法的调度方法。Lou G等[11]针对混合车间调度问题，通过添加保优记忆库，使用分组策略的工序调整结构，在引入交叉、变异运算符的基础上提出了改进的混合免疫遗传克隆选择算法。Zhang R[12]设计了一个评估工作瓶颈水平的模糊推理系统，以总加权拖延率为目标，提出了一种基于新型免疫机制的混合模拟退火算法。

以上文献基于FJSP问题的研究证明了智能算法的实用性，但由于智能算法属于概率搜索算法，存在收敛速度快、容易陷入局部最优解和种群质量低下等问题。基于此，该文提出了一种改进的免疫遗传算法。该算法采用多种策略的种群初始化方式，提出了抗体浓度的调节方式以及根据抗体浓度自适应调节的交叉算子、变异算子的构造方法，并利用种群分割的思想提高了种群的多样性和算法的收敛性。

1 FJSP问题描述

FJSP问题可以描述为：有n个工件需要在m台机器上进行加工，每个工件有Oij(Oij≥1)个工序，每道工序可供选择的机器数Oijk(Oijk≥1)，同一工序在不同机器上的加工时间不同。调度的目标就是在一定的约束下，找到最佳的加工顺序。

其数学模型如下：

(1)工件集：J={J1,J2,…,Jn}，Ji表示第i(i=1,2,…,n)个工件。

(2)机器集：M={M1,M2,…,Mm}，Mj表示工件Ji在机器集合M上所有可用机器的集合(j=1,2,…,m)。

(3)工序集合Oij={Oi1,Oi2,…,Oini}，Oij表示工件Ji的第j(j=1,2,…,ni)道工序。

(4)工序加工的时间矩阵T，tijk∈T。

tijk=eijk-bijk

(1)

其中，bijk、tijk、eijk分别表示工序Oij在机器Mk上的加工开始时间、加工时间和加工完成时间。

(5)约束条件。

①工序约束。

eij≤bi(j+1)

(2)

其中，bi(j+1)表示工件Ji的第j+1道工序的加工开始时间。

②机器约束。

各工序使用机器的总数为1次。

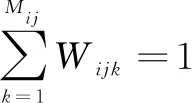
(3)

其中，Mij表示工序Oij可供选择的机器总数，且在时刻t(t>0)，如果∃Wijk=1，则对∀p或q，不存在工序Opq，使得Wpqk=1，

③时间约束。

所有工件在零时刻都可以被加工。

bij≥0

(4)

所有机器在零时刻都可以加工工件，且各机器之间相互独立，即某一机器出现故障并不会对剩余机器造成影响。

④工序的加工过程不会被中断。

(5)

(6)目标函数。

调度目标是使最大完工时间TM最小。

(6)

其中，Ti表示工件Ji的完工时间。

2 改进免疫遗传算法设计

2.1 算法流程

算法流程如图1所示。

贾宝柱(1974—)，男，辽宁阜新人，副教授，博士，研究方向为轮机工程。E-mail:jiabzh@gmail.com

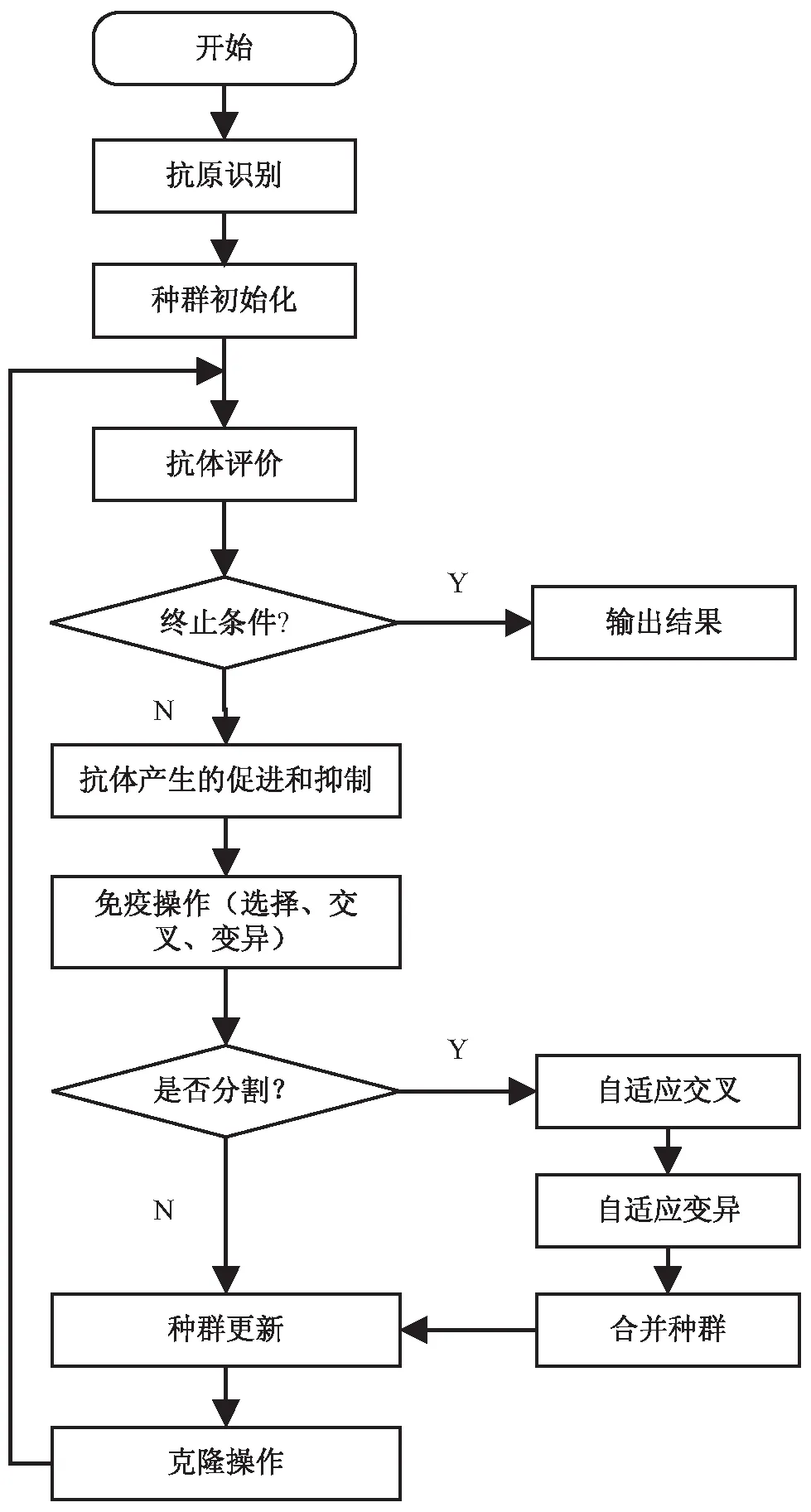
图1 改进免疫遗传算法流程

算法的具体实现步骤如下：

(1)分析问题。将目标函数和约束条件作为抗原，可行解作为抗体。

(2)产生初始抗体群。采用混合策略生成70%初始种群，剩余30%，采用多次迭代随机生成保留部分抗体的方法组成。

(3)抗体的多样性评价。以抗体的期望繁殖概率Pv为标准对抗体进行评价。

(4)终止条件判断。若满足算法的终止条件则输出结果，否则继续执行下步操作。

(5)抗体的促进和抑制。促进亲和力高浓度低的抗体，抑制亲和力低浓度高的抗体。

(6)抗体的产生。按照精英保留与轮盘赌相结合的策略进行克隆选择操作，并依据种群中抗体浓度的高低进行自适应的交叉和变异操作，产生新一代的抗体群。

(7)判断是否分割。根据预先设定的阈值，在新一代的抗体群中提取出亲和力较弱的抗体并再次进行交叉、变异操作。

2.2 改进免疫遗传算法求解FJSP过程

(1)个体编码与解码。

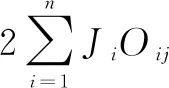
[1 3 2 1 2 3 2 1 3 1 3 2 3 4 5 1 2 4]

其中，前8位为工序的加工序列，即：O11→O31→O21→O12→O22→O32→O23→O13→O33，后8位为加工机器的序列，即：M1→M3→M2→M3→M4→M5→M1→M2→M4。

解码时采用文献[13]给出的前沿贪心方式解码成活动调度。首先根据基因串确定各工序的加工机器，然后根据各机器的可利用时间随机插入剩余工序。以此确定每台机器上各工件的加工序列。

(2)抗原识别。

抗原对应问题的目标函数与约束条件。抗体对应解决问题过程中产生的所有可行解。

(3)种群初始化。

根据上述编码原则利用最大工作剩余和最多工序剩余的思想在工序排序及加工机器分配的基础上采用混合方法产生70%初始种群。剩余30%，采用多次迭代随机生成的方法，在每次生成的抗体群中只保留部分亲和力较高的抗体。并将抗体群中亲和力较弱的抗体，在下次迭代过程中进行替代。以此为循环，直至达到随机生成的种群规模。

(4)抗体的多样性评价。

①抗体与抗体之间的亲和力。

借鉴Forrest等提出的R位连续方法计算[14]，即：

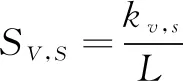
(7)

其中，kv,s表示抗体v与抗体s相同的位数，L为抗体长度。

②抗体与抗原间亲和力。

采用欧几里得距离作为衡量抗体与抗原亲和力的重要指标。针对整数编码，抗体v={v1,v2,…,vn}与抗原r={r1,r2,…,rn}之间的欧氏距离为：

(8)

亲和力为：

(9)

其中，Av,r反映了抗体v与抗原r之间的差异度，当dv=0，Av,r=1时抗体与抗原匹配度最高。

③抗体浓度。

抗体浓度Cv反映种群中相似抗体所占的比例，即:

(10)

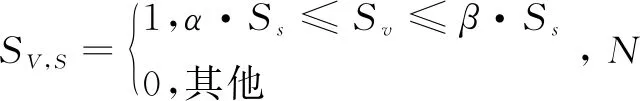
④期望繁殖概率。

在种群中，抗体的期望繁殖概率Pv由抗体与抗原的亲和力Av和抗体浓度Cv共同决定，即：

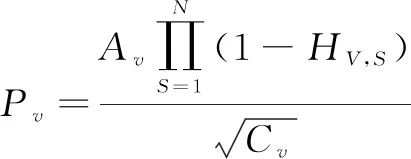
(11)

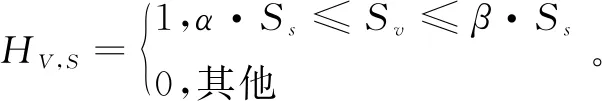
(5)免疫操作。

①克隆选择。

按照精英保留与轮盘赌相结合的策略进行克隆选择操作。这样在每次更新记忆库时，先将亲和力较高的抗体进行保存，再按照期望繁殖概率大小将种群中优秀的抗体存入记忆库。抗体被选择的概率即为式(11)计算出的期望繁殖概率。

②自适应交叉、变异。

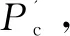
(12)

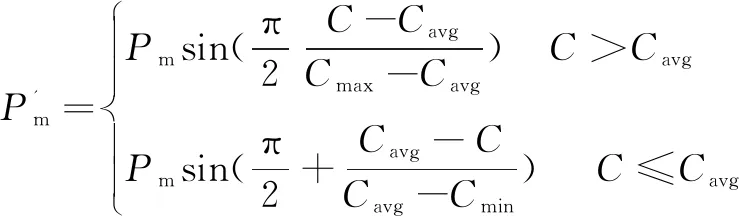
(13)

其中，C'为待交叉抗体的最大浓度，Cmax为种群的最大浓度，Cavg为种群的平均浓度，Cmin为种群的最小浓度，C为待变异抗体的浓度，Pc、Pm为交叉、变异概率的初始值。

(6)种群分割。

为了提高种群的多样性，以抗体的平均亲和力为标准，把未满足要求的抗体分割出来，进行再次交叉、变异操作，待提高抗体的亲和力后并入原种群中，进行下次迭代。

(14)

α2(i)=cross & mutation(α1(i))

(15)

α=combine(α(N-i),α2(i))

(16)

其中，α(i)为分割前的种群，α1(i)为分割后的新种群，α2(i)为经过再次交叉、变异后的种群，α为合并后的种群，Ai为抗体i的亲和力，Aavg为种群的平均亲和力，Pt为种群的分割概率。

(7)克隆记忆。

在经过以上操作后会产生大量的可行解，将效果最好的可行解即最小的目标函数值，与记忆库中的抗体进行比较，如果大于记忆库中抗体的亲和力则替换相应的记忆细胞，然后对其进行克隆操作。

克隆操作就是把最接近最优解的抗体根据亲和度的不同按照不同的尺寸复制成多个抗体的过程，抗体的克隆规模qi为：

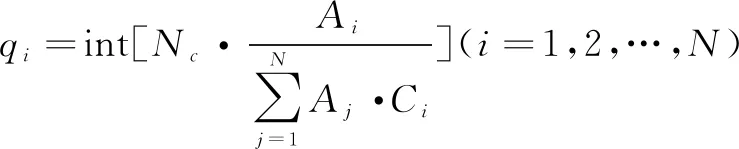
(17)

其中，Nc为种群总的克隆数目，int为向下取整，qi为第i个抗体的克隆数目。

3 仿真实验与算法比较

为了全面验证算法性能，选取文献[15-19]中的基准算例作为测试对象。算法程序是在MATLAB 2018a的基础上实现，在处理器为Intel(R)Core(TM)i5-5200U CPU、RAM为4 GB、运行环境为Windows10(64 位)的个人计算机上进行仿真测试。实验参数设置如表1所示。

表1 实验参数

首先选取4×6FJSP算例，具体信息见表2。其中-表示该工序不能在此台机器上加工。根据表2进行仿真实验20次，得到如图2、图3的仿真结果。

表2 4×6FJSP加工时间

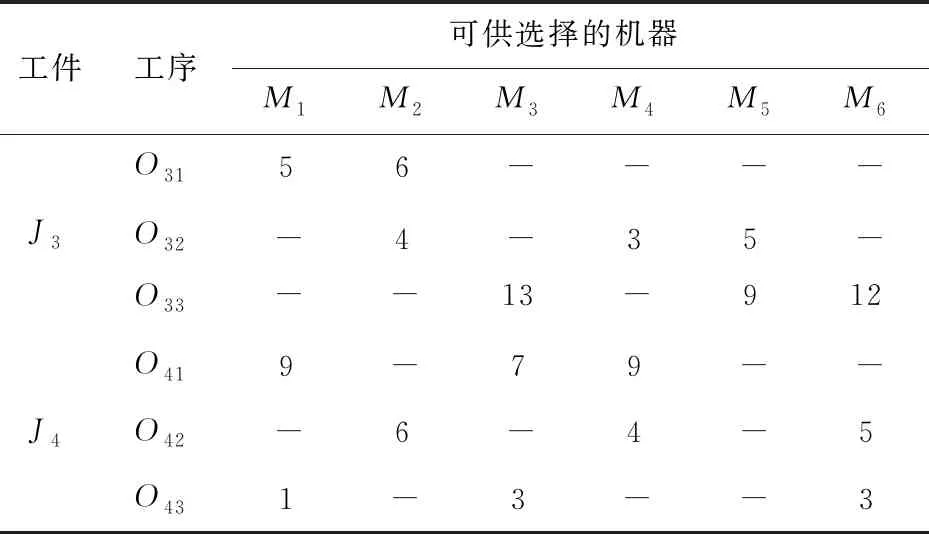
续表2

图2 4×6算例仿真甘特图

图3 4×6算例仿真收敛图

由表3可知，文中算法的最优完工时间为17 s，与文献[16]相比算法搜索能力较优。文中算法的平均收敛代数为7.8，与文献[15,17]相比算法的收敛速度快，效率高。在20次的仿真实验中，文中算法17次得到最优解，与文献[15,17]相比算法的求解稳定性较好。

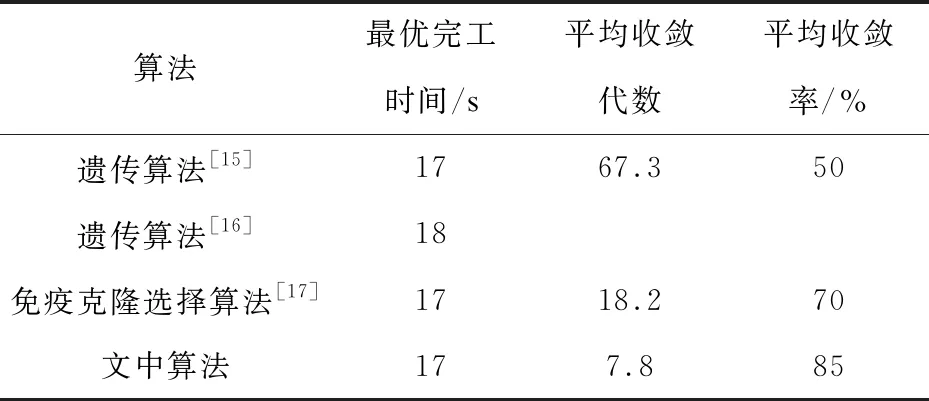
表3 4×6算例不同算法仿真结果对比

为进一步验证算法的可行性，选取6×10FJSP算例对算法性能进行再次验证，同样选取以上参数并独立运行20次。其仿真结果如图4和图5所示。

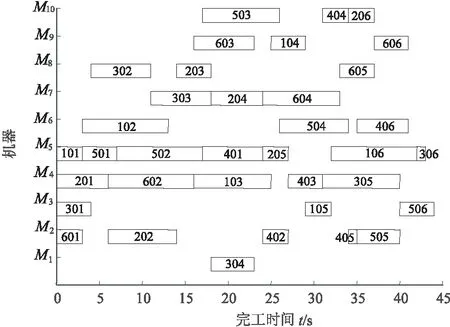
图4 6×10算例仿真甘特图

图5 6×10算例仿真收敛图

由表4可知，文中算法的最优完工时间为44 s，与文献[17-19]相比算法用时最少，算法最优解的搜索质量较高。文中算法的平均收敛代数为19，与文献[17-19]相比算法收敛速度快，效率高。在独立运行20次中，文中算法平均进化率为80%，高于文献[17,19]的进化率，算法的求解稳定性较好。

表4 6×10算例不同算法仿真结果对比

4 结束语

针对智能算法在解决柔性作业车间调度问题中的不足，在对免疫遗传算法的种群初始化方式、抗体的浓度及期望繁殖概率调节的基础上，提出了新的种群初始化方式、抗体浓度的调节方式及依据抗体浓度自适应调节的交叉算子与变异算子的设计方法，并以种群的平均亲和力为标准对种群进行分割操作设计，保证了种群多样性，提高了算法的收敛能力。最后通过与其他算法进行横向测评，验证了该算法的有效性。