EMD融合WPT和CSP的脑电特征提取方法

张学军，刘定宇，霍 延

(1.南京邮电大学 电子与光学工程学院、微电子学院，江苏 南京 210023； 2.南京邮电大学 射频集成与微组装技术国家地方联合工程实验室，江苏 南京 210023)

0 引 言

脑机接口(brain computer interface，BCI)是涉及众多学科和知识领域的控制技术。脑机接口的概念于二十世纪末期被首次提出，它建立了人脑与外部设备的通道，通过采集脑电信号，使用分类算法来识别人脑的指令[1]。脑机接口技术在近几十年取得了极大发展，应用领域也越发广泛，尤其在运动障碍患者的康复训练中得到了大量的应用，病人通过该技术提高了与外界的交互能力和自理能力。通过大脑信号，可以直接控制相关的外部设备，如计算机、机械小车，机械假肢[2]等，这些应用都增强了他们与外界的交流并加快了他们的恢复。脑机接口技术还被广泛地应用于其他一些领域，如游戏应用和导航[1]。

脑机接口技术包含信号采集、预处理、特征提取、分类以及外部设备控制。特征提取用于识别不同脑电信号的特征信息，因此在脑机接口的研究领域备受关注。之前研究的比较成熟的方法如短时的傅里叶变换(short-time Fourier transform，STFT)、小波变换(wavelet transform，WT)等等，由于EEG信号的非线性以及非平稳性，这些传统方法不能得到理想的分辨效果。经过近年来不断的研究，希尔伯特黄变换(Hilbert-Huang transform，HHT)得到了发展，经过验证能够更好地对EEG信号进行分析。采集的脑电信号，首先经过EMD[3]分解后得到一串的IMFs，随后通过HHT可以得到相应的能量谱数据，得到的数据可以作为一个特征指标，用于后续的分类。HHT被提出后，其优秀的性能，集中的特征和较高的分辨率，使其应用越发广泛[4]。对于EEG信号，目前方法得到的分类效果都无法达到期望，如需应用在BCI系统中，需对其进行更复杂的处理，可以先进行空间范畴的滤波，获得高质量的信号，提取更优质的特征信息。常用的算法包括公共空间模式CSP[5]，以及独立分量分析、滤波器组公共空间模式、判别滤波公共空间模式等改进的CSP算法[6]。传统的经验模式分解在低频区域首次得到的固有模态函数涵盖过宽的频率范围，无法得到单组份的属性，且不能分开含有低能量成分的信号。为了弥补此类问题，该文提出了一种改进方案，即在传统的EMD分解之前，使用小波包变换对信号进行处理将原始的信号分为一组窄带信号，并利用筛选去除不相关的固有模态函数。同时常规的公共空间模式分解方法在通道数及频域方面都有明显的缺陷[7]。为了弥补这些短板，该文将EMD和CSP算法相结合，筛选IMF频段，剩下的计算其能量的特征，使用CSP滤波器，得到其特征的一组数据，最后使用SVM进行分类，可以达到95.9%的平均分类准确率。

1 相关算法

1.1 经验模式分解

EMD因为在非线性序列处理方面的优越性而被广泛用于处理非线性数据。在时间域中研究其本征波动模式[8]并进行分解是其核心的思想。这种分解过程，可以将其理解为筛选的过程。需要有以下条件：(1)需得到数据的极值；(2)需知两个极值之间的时间间隔定义的特征尺度；(3)如果未满足上述条件，但是函数存在拐点并可以通过微分的方法经过一次或多次求得极值也可以被认为满足条件，但是需要注意分解结果也相应需要通过积分获得。

EMD分解具体步骤：

步骤一：读取信号x(t)的所有极值信息，然后用三次样条函数对它们进行处理，得到序列的包络线信息，上包络vmax(t)，下包络vmin(t)，以此进一步得到包络线平均值m(t)。

(1)

步骤二：计算原信号与均值的差值c(t)：

c(t)=x(t)-m(t)

(2)

IMF定义的截止条件：在时间域内，极值个数等于过零点的个数，或最大差值为1，且最大信号幅度形成的包络线和最小信号幅度形成的包络线算术平均为零，如果不满足，就重复上述过程，剩余量r(t)的公式为：

r(t)=x(t)-c(t)

(3)

步骤三：作为一种新数据，剩余量通过同一过程过滤，得到下一个低频固有模函数。直到剩余函数r(t)得到的是单调函数或只有一个极值分解的过程才会终止。假设将原始信号x(t)进行分解，得到了n个本征模函数和一个剩余函数r(t)，重构信号如下：

(4)

1.2 公共空间模式

目前基于运动图像的BCI系统中有功率谱密度[9]等方法。CSP就是一种常见的处理方法。其对输入的脑电数据进行映射处理[10]，通过这个过程获得的特征向量可以得到较好的分辨度。它以两个不同类别的协方差矩阵作为基础，通过对角化处理设计最优化的空间滤波器。对原始EEG数据进行映射，获得最大程度上的分离[11]。具体步骤为：

步骤一：设定单次想象运动的脑电信号矩阵为X(N*I维)，其中N表示EEG采集的通道数而I表示各通道的采样点数．这里将X进行归一化处理以此得到相关的协方差矩阵：

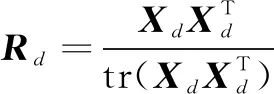
(5)

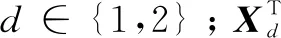
步骤二：对合成的协方差矩阵进行分解。

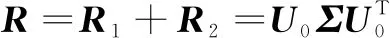
(6)

其中，Σ为特征值对角矩阵，U0为其对应的特征向量矩阵，其随相应的特征值而重新改变。

步骤三：求白化矩阵，白化矩阵P定义如下：

(7)

步骤四：白化协方差矩阵R1和R2。

(8)

步骤五：主成分分解。

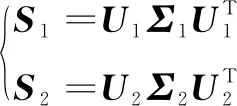
(9)

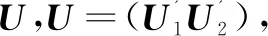
步骤六：求CSP的空间滤波器W。

W=UTP

(10)

运动图像脑电信号x，经空间滤波z=wx，得到z，特征向量数为2m。为使两个样本得到最大距离，前m个特征向量，取它们与一类运动想象方差的最大值，后m个则取最小值。而后面剩下的m维则使用相反方法[12]。其中第1个和最后1个特征向量，有最大的区别度，第2个和倒数第2个相比较小，以此类推。所以应选取合适的向量个数以使其包含最佳的特征信息。

步骤七：特征提取后，再将空间投影后的信号Zp(p=1,…,2m)取对数，从而使特征值差异更明显，其中var表示求向量的方差。

(11)

1.3 支持向量机

支持向量机(SVM)[13]，为了得到更好的分离特征向量，将低维信号通过映射的方式放到高维度的特征空间，用超平面的分类方式对数据进行下一步的处理。超平面的概念可以理解为，高阶的数据须由低一维的数据进行分割处理，比如，用一条直线划分一个二维的平面区域，用一个二维的平面来分割一个三维的立体。所以如何选取一个最好的超平面是其主要的关注点，做到分类间隔尽量大，这样准确率就可以得到提升。同时，核参数和误差惩罚因子对向量机的分类也有很大的影响。

2 EMD结合WPT和CSP算法

2.1 经验模式分解改进

传统的EMD在低频区域会产生不理想的固有模态函数，且首次得到的固有模态函数涵盖太宽的频率范围，无法得到单组份的属性，同时也不能分开含有低能量成分的信号。该文提出了一种改进方法来弥补这些不足，在传统的EMD之前，先使用小波包变换对信号进行处理，将原始的信号分为一组窄带的信号，并且利用一个筛选过程从结果中去除不相关的固有模态函数。

2.1.1 小波包变换过程

为了解决上述问题，这里先使用了小波包变换。

对于一个n层的分解，信号被分为2n个窄带信号。由于分解是基于频率而不是基于能量，因此，低能量成分被分解为不同的频带保留下来。所以，小波包变换首先用来得到若干窄带信号，然后对这些窄带信号进行分解，于是得到的固有模态函数同样有窄频带而且它们的瞬时频率更加接近IMF的真实频率模式。

由于脑电信号强度较弱，且采集的时候有如眼、肌电等众多的影响源因素，这些相对的噪声都会影响脑电信号的质量。所以该文使用了小波包变换，以此在频域对其进行过滤，有效地提高了脑电信号的信噪比。小波包变换源于小波变换，所以不仅继承了其优点，更是在基础上有部分改进。它对信号进行正交分解，同时对于频段的选择更加准确，能更好地匹配信号的有用频段，获得更有效的频谱信息，因此其分辨率也得到了提高。小波包变换的这种多分辨率特性可以在所在的频率范围内锁定更加有用的信息。在小波多分辨率信号分析中，希尔伯特空间可以变换不一样的尺度指标分解得到所有的小波子空间的正交和，并根据二进制系统进行细分，如图1所示。

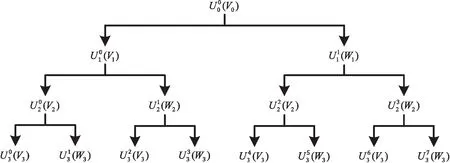
图1 小波包的空间分解

2.1.2 筛选过程

此处将信号和IMF的归一化相关系数μ作为标准来对固有模态函数进行筛选。

获得所有的相关系数[14]μi(i=1∶n，n是IMF的数量)，然后通过下式计算硬阈值：

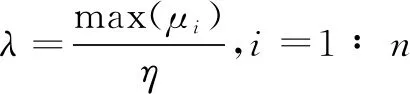
(12)

其中，η(>1)是一个比例系数，经验值为10。每一个固有模态函数都和λ进行比较，如果一个固有模态函数的相关系数大于λ，相应的固有模态函数就保留；如果不符合上述要求，相应的固有模态函数就被删除。

该文考虑了两种筛选过程，第一种用来排除由WPT得到的窄带信号关联性较差的IMF；第二种用来去除由窄带信号产生的弱相关的IMF，这些窄带信号本身就与原始信号相关性很差。

2.2 改进EMD结合WPT和CSP算法流程

该文提出的改进方案，通过采集获得脑电信号后，经由滤波器先进行预处理。接着在传统的EMD分解之前，使用小波包变换对信号进行处理，将原始的信号分为一组窄带信号，筛选去除结果中相关较差的固有模态函数。同时再将EMD和CSP算法结合，筛选IMF频段，剩下的计算其能量的特征，使用CSP滤波器，得到其特征的一组数据，最后使用SVM进行分类。算法流程如图2所示。

图2 算法流程

3 数据集描述

为了便于与经典方式进行比较实验，采用BCI2008年的竞赛数据。实验设备包括电脑及电极帽等脑电采集设备，受试者头戴电极帽坐于屏目前约1米处，根据提示做相关运动想象同时采集相关脑电信号。数据包含9名右利手的受试者的脑电数据。实验开始时，受试者保持放松并坐于距离屏幕1米处。实验中，屏幕上会显示不同方向的箭头作为想象的提示，受试者根据提示进行想象运动。在两天里完成两个session，每次session6个run，每个run20次实验，左右手分别10次。所以在一次session中，左右手各60次。

实验界面和时间序列如图3所示。

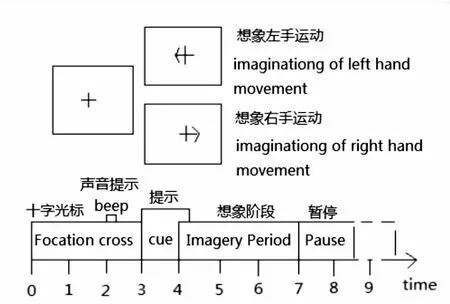
图3 实验界面和时间序列

每一次实验的时间，大概8至9秒，前两秒放松；第二秒的时候会出现提示音指示实验开始，屏幕上这个时候会出现一个十字型的光标提示预示着开始进入准备状态，时长1秒；第三秒的时候屏幕上会随机出现向左向右的箭头并持续1.25秒；第四秒开始根据屏幕的箭头提示，受试者进行3秒的想象运动并在第7秒时停止。使用Ag/Agcl电极,记录C3，Cz，C4三个通道的数据。C3和C4两个电极采用的脑电数据对应运动想象最活跃的脑部部位，同时将Cz作为参考的信号。选用0.5 Hz～100 Hz的带通滤波器。

4 实验分析

4.1 小波包分解

根据事件相关同步/去同步原理，进行想象运动会在相关的频率段产生能量的变动，因此，相关频段μ节律，β节律的脑电就非常重要。信号频带宽100 Hz，这里将脑电信号进行4层分解，分解后得到16个不同的频率段。其中最小的分辨率如式(13)所示。

Δf=100/16=6.25 Hz

(13)

频段分解后，子带信号所对应的频率范围如表1所示。

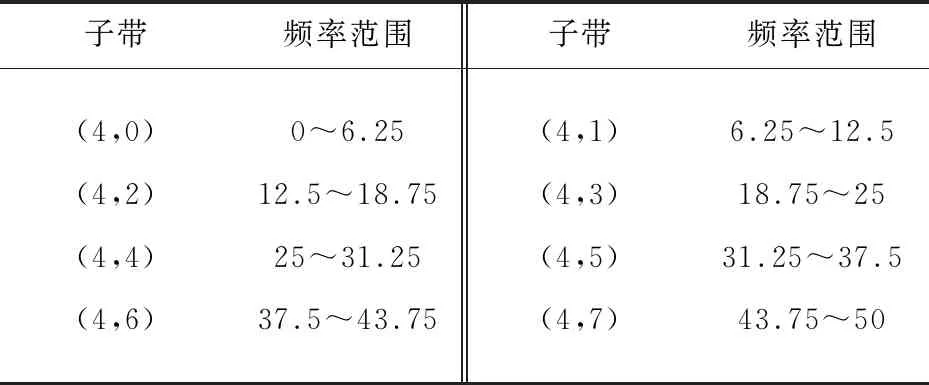
表1 各子带所对应的频率范围 Hz

当进行左右手想象运动的时候，μ节律变化主要范围为7 Hz～13 Hz，β节律在19 Hz～26 Hz。对照表1，μ节律主要落在子带(4，1)中，而子带(4，3)可以看到β节律的频段，所以，重构(4，1)及(4，3)子带，提取到μ节律和β节律脑电，保留相对有效的脑电信息，可以更好地提取特征。图4分别展示了两个子带重构后的波形及频谱状态，可以看出重构后的子带频谱显示出更加集中且明显的特征。

图4 小波分解子带信号(上：波形，下：频谱)

4.2 EMD分解结果

对脑电信号进行单纯的经验模式分解会产生频段涵盖宽泛的问题，同时在低频区域会产生不理想的IMFs，不能分开含有低能量成分的信号，从而会使结果产生错误。为了弥补这些不足，在EMD之前进行小波变换将信号分为一组窄带信号，选取合适的子带信号，分解为频率更加集中的固有模态函数。

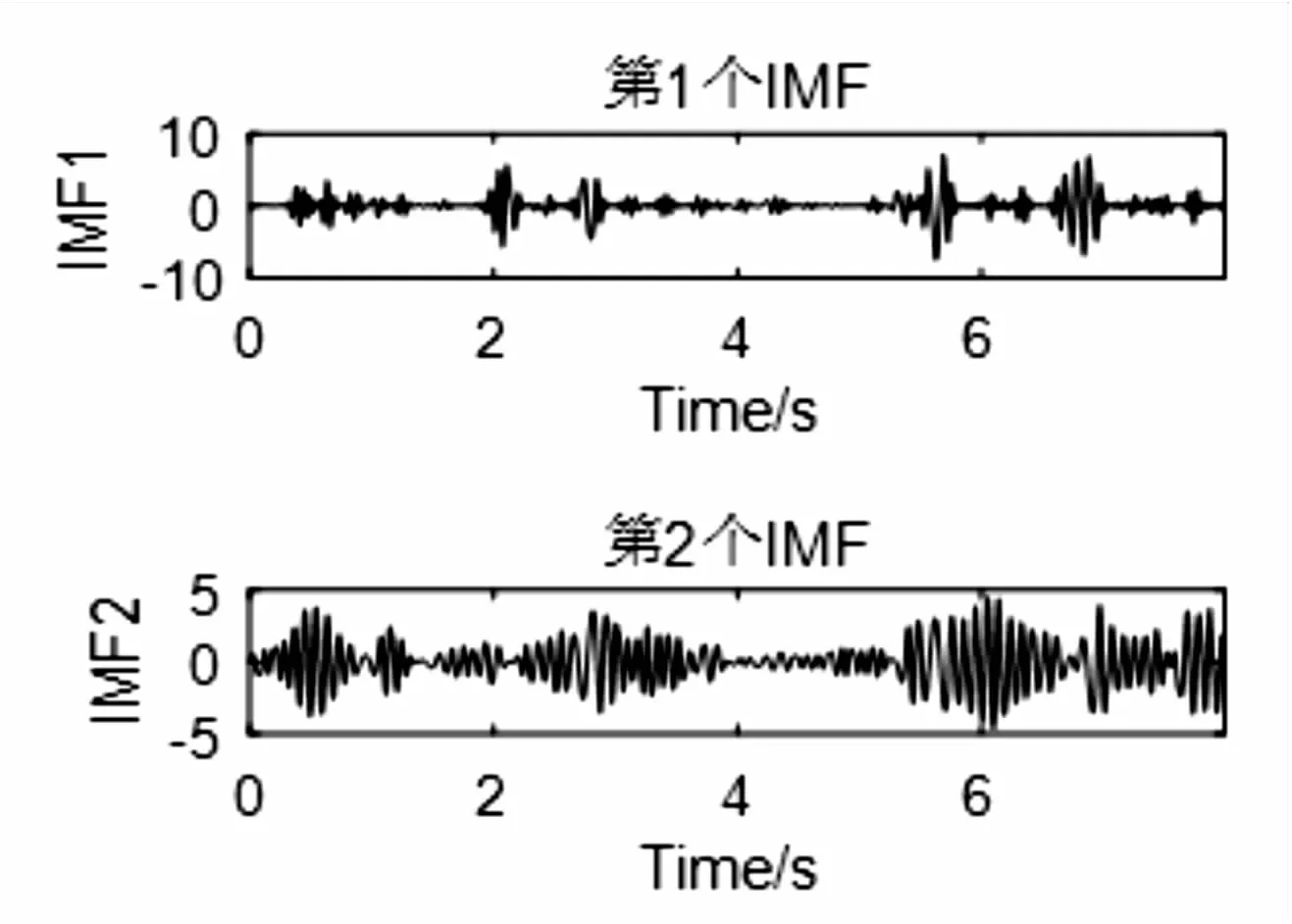
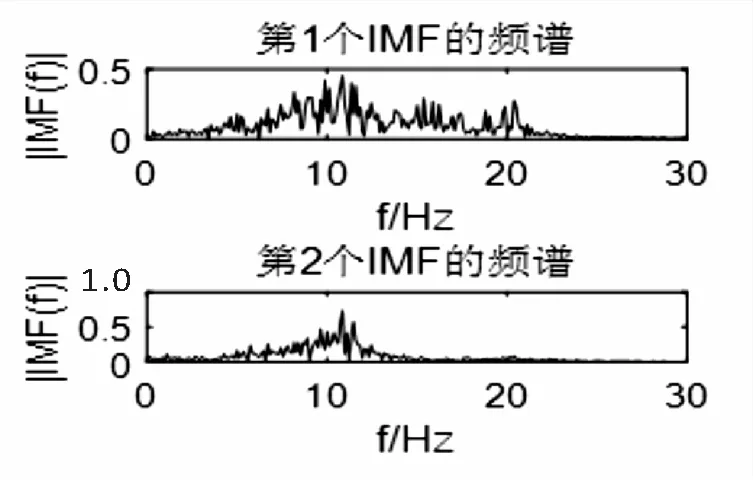
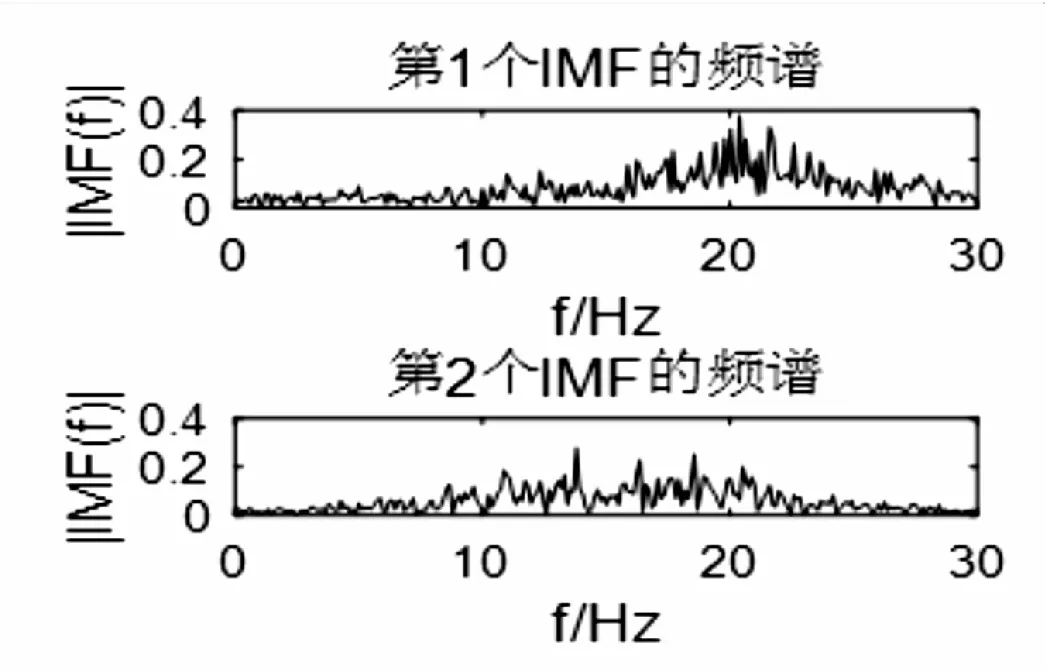
利用EMD对WPT处理后的子带信号进行处理。前两阶IMF的相关系数远大于剩余的IMF，可见前两阶IMF有EEG信号最主要的信息，将最活跃的频段包含在内，而剩下的IMF则多包含噪声及无用的信号，因此被舍弃。所以该文选择仅重构前两阶IMF。这里EMD的目的就可以看作是提取μ节律和β节律。同时，该方法可以获取更多有效的信号，提高整个脑电信号的信噪比。图5和图6分别展示了(4，1)、(4，3)子带信号经过EMD分解后前两阶的IMF信息。

通过图5和图6可以看出，得到的两个子带具有比原始信号更大的有效范围，包含了最活跃的频段信息，且信噪比也更加优越。

(a)时域图

(b)频域图

(a)时域图

(b)频域图

4.3 CSP滤波

在使用EMD之前，该文提取相关EEG信号，选取C3和C4通道的数据，并通过WPT得到一系列窄带信号。然后对相应的子带信号进行EMD分解得到多个IMFs。选取前两阶作为新的输入，形成矩阵XI(X=L左手，I=R右手)。选取两子带信号(4，1)、(4，3)，经EMD分解并选前两阶IMFs。

4.4 实验结果分析

将每次试验得到的数据，先经WPT分解，选取子带信号，然后进行EMD分解，选择IMF，组合并重构前两个IMF分量，接着利用CSP进行特征提取。图7为单个实验中的前两个IMF分量经过滤波后的脑地形图。

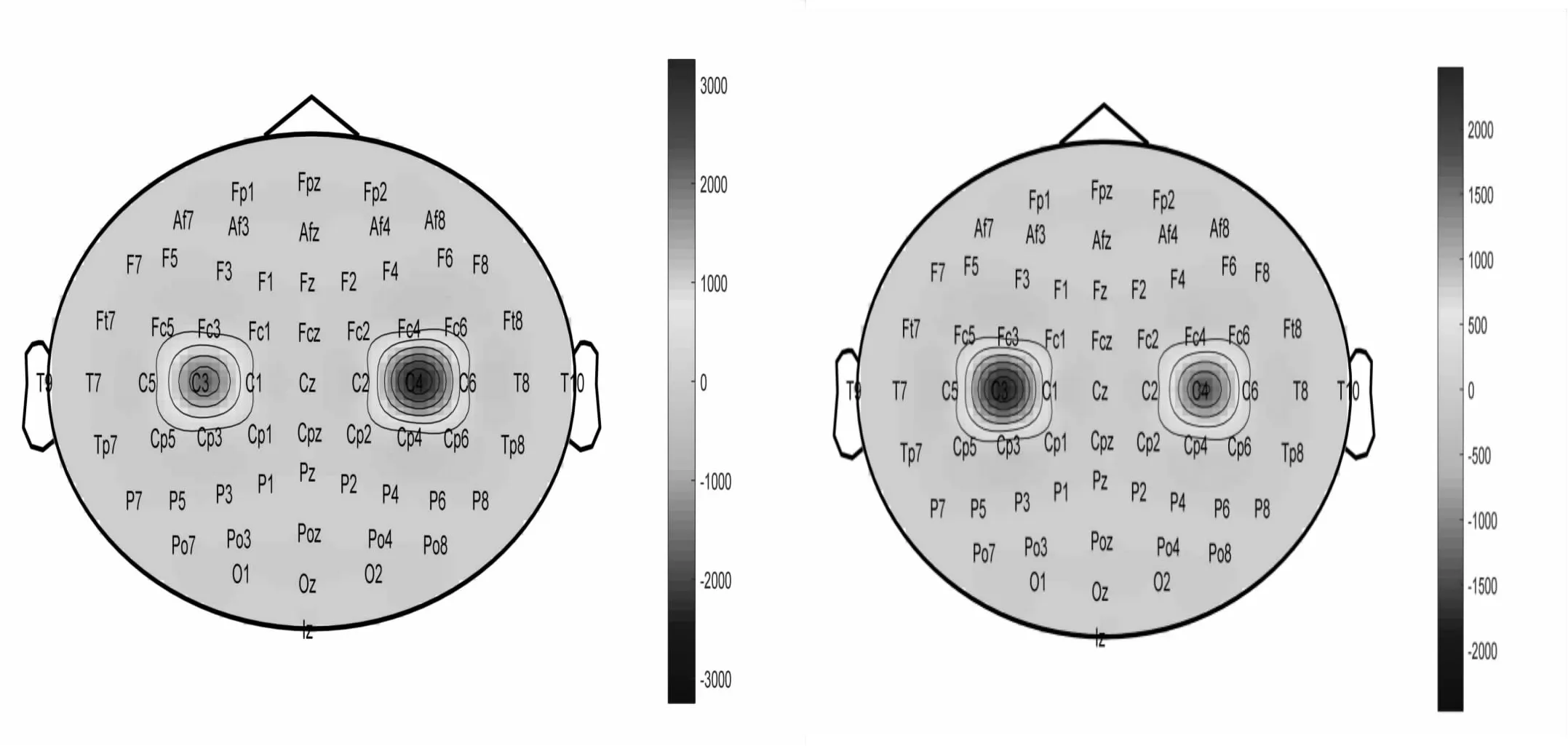
图7 想象运动前两阶IMF的脑地形图

可以看到，C3和C4电极在两个不同的想象运动之间的能量差异很大。在想象左手运动中，C4电极的活跃度明显高于C3电极而当想象右手的动作时，两个电极处于相反的位置，变为C3更为活跃，这样的结果符合了运动想象中的同步去同步特性。观察实验结果，图8展示了9位受试者所有实验的平均分类正确率。

图8 平均分类准确率比较

可以发现，文中的分类方法可以达到 94%～98%的准确率。9位受试实验得到的平均分类准确度基本上都在94.6%～96.4%，平均准确率为95.9%。

最后，对比该方法与之前的竞赛中不同算法的分辨率。在一样的数据集下，该方法的分类精度相比其他三组在分类准确度上有了一定提高。同时，该文只对两个通道信号进行采集，得到了较好的分类精度，也减少了脑电采集的信道数和数据量。 表2展示了之前的算法和文中方法的分类结果。

表2 BCI竞赛成绩和文中结果比较

5 结束语

为了弥补传统的EMD算法及CSP算法的缺点，获得更好的分类效果，提出了EMD结合WPT、CSP的特征提取方法。先对EEG信号进行预处理，对原始信号进行滤波去噪，接着用WPT将信号分成一组窄带信号,处理后的信号经EMD得到多个IMF分量。不相关的固有模函数被屏蔽和消除。然后将处理后的信号的功率谱密度作为CSP滤波的特征进行计算。最后使用SVM分类。实验结果表明，该方法在通道的减少和分类精度的提升上，相对之前的原始方法都有一定的进步。