基于经纬映射与透视投影的球形图像校正

覃 丹，崔 岩,2，刘兴林

(1.五邑大学 智能制造学部，广东 江门 529000； 2.珠海四维时代网络科技有限公司，广东 珠海 519000)

0 引 言

在这十几年中，人们越来越容易获得具有广角360°视场的球形全景图，通过具有特殊镜头的摄像机，甚至是通过能放进口袋的手机也能拍摄出广角360°视场的球形全景图。球形全景图像已成功应用于在线街道级虚拟导航(Simon Hecker等，2018)、城市规模变化检测(方旭等，2017)、场景识别和视图检测(宗海燕等，2019)和3D场景重建(王资健等，2018)等方面。

然而，球形全景图像更大范围的视角效果和广泛的应用面临着这样的困境：图像校正是许多计算机视觉任务的基本问题，但是广角360°视场的球形全景图校正的研究远远少于广角180°左右视场的鱼眼图像及平面图的校正。球形全景图与其他图片的视觉效果相比，视角范围更大，能将更多的事物容纳到视角里，并且突显出所拍摄的事物近大远小的对比效果，使所拍摄画面形成一种震撼人心的视觉效果。但是也正因为球形全景图具有广角360°的视场，所以图像畸变严重，特别是越靠近图像边缘的地方视场越模糊。

一些针对鱼眼图像设计的校正算法被提出，如王向军等人[1]提出的基于改进球面透视投影的鱼眼图像畸变校正方法和张军等人[2]提出的单幅圆形鱼眼图像的校正，但是他们提出的经纬映射校正法是针对鱼眼图像的；而变角度线扫描法和纵向压缩柱面投影校正法，在垂直方向上的校正效果较好，在水平方向上的弯曲校正效果还不是很理想。对平面图像的校正也有研究，B.Hallert首先使用最小二乘法处理摄像机校准中获得的观测数据，从而在现场测量中获得高精度结果[3]。Aziz和Karara在20世纪70年代早期提出了直接线性变换(DLT)相机校准方法。从摄影测量的角度，深入研究了摄像机图像与3D世界之间的关系，建立了线性模型。线性模型易于计算且速度快，但很难完全表示相机的非线性失真特性[4]。在20世纪80年代中期，R.Tsai提出了一种基于RAC的校准方法，并建立了经典的Tsai相机模型。该方法的核心是利用线性模型求解线性参数，然后根据径向均匀约束迭代求解非线性参数。基于RAC方法的失真模型降低了参数求解的复杂度，校准过程快速准确[5]。后来，基于最大似然估计的非线性细化将平面四边形的各个角及其对应的图像点之间的几何误差最小化以解决相机参数。Zhang等在2017年提出使用RANSAC算法来改进校准参数,基于对象的相机校准的性能高度依赖于对象的准确性。通过以上分析，可以看出目前针对球形图像校正的应用较少。

因此，为了解决球形全景图图像变形问题，以适应人眼的视觉或增加图像识别技术等对球形全景图利用的实用性，该文提出一种基于经纬映射与透视投影的球形图像校正方法。

1 相关工作

为了利用球面全景图像，应该考虑球形全景图像中包含的严重失真。关键点、角点和特征点因扭曲而受损。因此，需要克服球形全景图像的严重失真。当物体的投影远离图像中心时，径向畸变变得更加严重[6]。球面全景图像具有与径向畸变类似的非线性放大率，将其称为球面畸变。当物体的投影位于靠近极点时，球形畸变变得更严重。由于球形全景图像中物体的球面变形基本上与径向畸变非常相似，因此在进一步研究之前研究径向畸变是有帮助的。Lourenco等人[7]将径向畸变表示为非线性几何变形，其使像素位置沿径向方向并朝向畸变中心移动，他们提出了一种改进SIFT算法为径向畸变[6-7]。径向畸变是由于非平坦的镜头特性和相机镜头的不完美制造工艺造成的，使用广角镜头拍摄的图像会产生严重的扭曲。Zhang Zhengyou提出了一种灵活的平面校准方法，可以简化摄像机校准过程，同时获得高精度的校准结果。该方法基于不同角度和姿势的黑白棋盘模板拍摄三张或更多图像，提取图像中棋盘的角坐标，并替换建立的相机模型方程，以获得内部和外部参数以及失真系数。后来，开发了基于圆形模板，六边形网格图案等的校准方法[8-9]。该文的球形图像校正也需要确定图片中的相机位置，文中的数据源为球形图，因此校正过程还需计算图片的圆心及半径数据，以此建立校正模型。

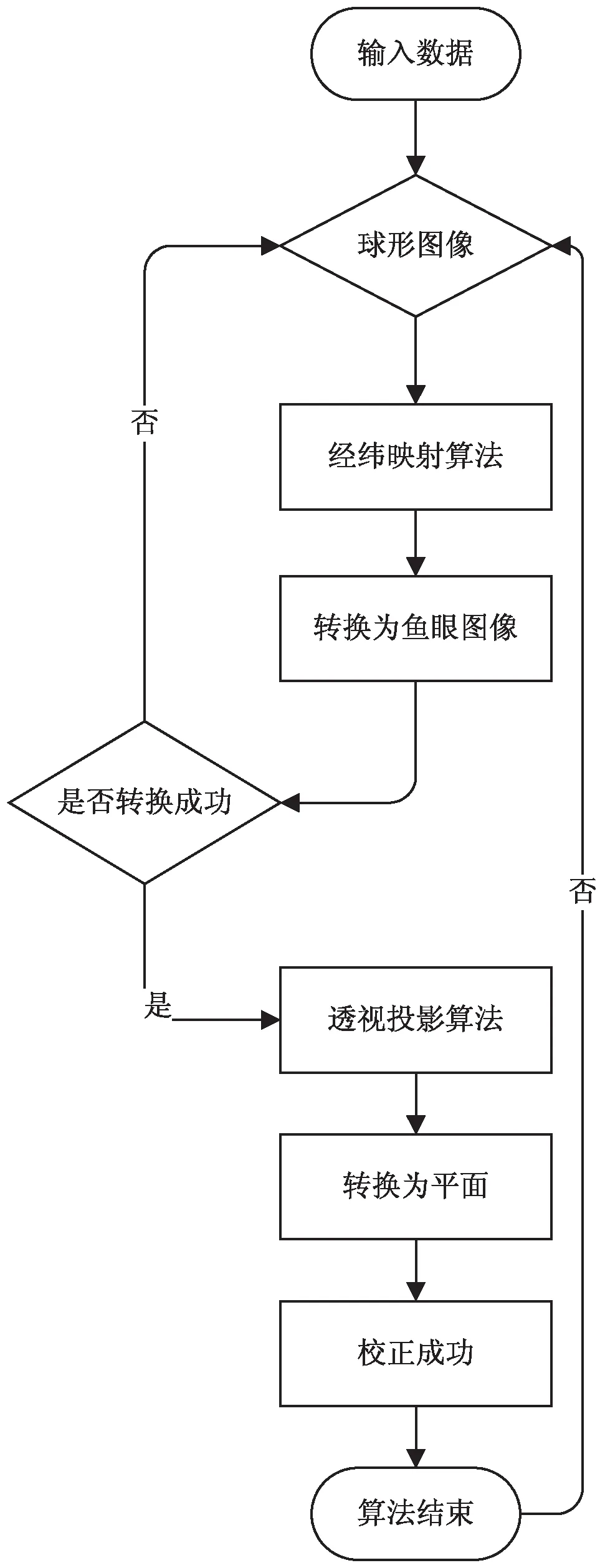
图1 工作流程框架

该文提出一种基于经纬映射与透视投影的球形图像校正方法。该方法首先是对经纬映射算法进行改进，将球形全景图通过改进的经纬映射法转换成鱼眼图；其次通过改进的透视投影算法将鱼眼图像进行最终校正。这样做是为了降低球形图像直接校正的难度。通常球形图像的广视角为360°，其计算的复杂度与存储的难易程度都远远高于广视角为180°的鱼眼图像[10-11]，因此，该算法先将球形图转换成鱼眼图，再对鱼眼图像进行校正处理。工作流程框架如图1所示。

2 球形图像校正算法描述

2.1 经纬映射算法

球面全景图像可以表示360°，描述了球形全景图像的几何特征。使用球形全景图，可以利用宽视角的优势。普通的平面相机具有有限的视角，并且所获取的视图还会受到相机的观看方向的限制。然而，无论观察方向如何，球形相机都覆盖整个视图。文中将球形全景图上的点通过经纬度映射为鱼眼图像的点，经度映射成鱼眼的水平坐标，纬度映射成垂直坐标，因为源图是整个单位球面，所以经纬映射图长宽比为2∶1，经度从0到2π，纬度从0到π[12]。地球上的任何点都可以用球坐标来描述，假设地球是一个单位球体，地理坐标系类似于球面坐标系。单位球形全景图像中扭曲的场景可以用图2中的经纬度定位图来表示[12]，图2中每一条经度上的像素点的列坐标对应着经纬映射后鱼眼图像的列坐标。假设图2垂直方向上同一经度有不同的纬度值Yi，并且Yi与Yi+1之间的角度差都为θ，此时由图2中看出在赤道上几乎没有拉伸变形，但是当同一纬度有不同的经度值Xi时，越接近南北极点，变形就越厉害[13-14]，几乎拉伸到图像的整个宽度。

图2 经纬度定位图

该文在对球形全景图求取中心点和半径之后，使用经纬映射图像的方法，将球形全景图像转化为半球的鱼眼图。从图2中可看出，因为源图像球形全景图像是单位球，目标图(球形全景图像映射的经纬映射坐标系图)和球形全景图像的尺寸一样，所以可以采用一一映射方法实现结果。如果源图像是半球单位，需要映射的结果为平面图或180°视角内的图像则采用多对一的映射方法，以避免在目标图上留下许多空隙点。

实现经纬映射算法的过程中还需要推导球形全景图像投影鱼眼图像与经纬映射图之间的映射关系。如图3(a)所示，假设有球形全景图像规格化坐标后映射为鱼眼图像上的某一点坐标为，计算P点到原点O的距离r及P点与X轴的夹角φ。图3(b)中显示了球形全景图映射时的球坐标。计算r和φ的公式[12]如下：

(1)

(2)

如图3(b)所示，r可以映射成球坐标系的θ、φ值，φ值可直接用于从照相机到实景方向向量的球坐标的φ，而θ角的值等于r乘以球形全景图视角α(文中选用的球形全景图默认视角为2π)的一半[12]。即:

θ=r*α/2

(3)

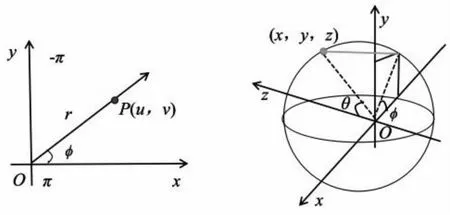
(a)极坐标平面 (b)球坐标选取

如图3所示，如果知道照相机到实景方向向量(x,y,z)，就可以推导出在经纬映射图中对应的坐标。由于在球形全景图到经纬映射图时的球坐标和球形全景图映射时的极坐标一样，因此假设有图3(b)的球坐标系(θ、φ)，θ是照相机到实景方向向量与y轴的夹角，φ是方向向量在XOZ平面上的投影与X负轴的夹角，若球面半径为1，则从照相机(球原点O)到实景中点的方向向量(x,y,z)公式[12]如下：

(4)

这样对于目标图像(所得到的鱼眼图像)上每一个像素坐标点，经过经纬映射的变换，可以映射到源图上的像素点，然后将目标图上每一点到源图的像素点取样，这样球形全景图就可以映射成鱼眼图像，为接下来的校正球形全景图像实验简化了实验复杂度。

2.2 透视投影算法

最后结合改进的球面透视投影算法实现最终的实验效果，即展开成平面图像。球面透视投影与平面透视投影原理一样[15]，需要知道球面上的点与投影面[16](文中的球面是鱼眼图像，投影面是鱼眼图像投影后的平面)的关系。如图4所示，假设有XFOFYF为鱼眼图像平面像素坐标系，并在XFOFYF上取得一点O，以点O为原点在XFOFYF上建立空间直角坐标系O-XYZ，X轴和Y轴方向向量与XFOFYF平面重叠，并以O为球心建立空间半球体，半径为r，称此半球体为鱼眼图像。当Z轴与映射后的平面图(主视图)的法线平行且经过主视图的原点Or时，OT与空间直角坐标系原点O距离为d。

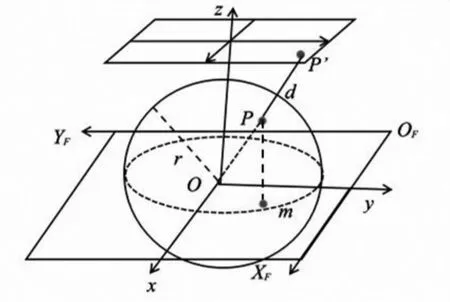
图4 鱼眼图像映射示意图

若平面图上有一点P(xp,yp)，与球心距离为dp，在球面上投影点是P，P点垂直映射点为m，在像素坐标系XFOFYF中m(Xm,Ym)满足如下关系：

(5)

(6)

假设鱼眼图像上有点m(Xm,Ym)映射到主视图上点P(xp,yp)，它们的关系可以用如下公式表示：

(7)

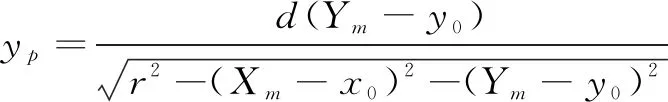
(8)

3 实验和讨论

为了评估文中算法的性能，进行了多组实验测试并将其与其他几种算法进行比较。文中选出一组室内与室外的两张图片进行展示，对于这两张图片分别采用文中算法、经纬映射算法+文献[12]算法(后文中都称为球形图坐标算法)、文献[17]算法(后文都称为球形图立体纹理映射法(sky box))进行测试，并比较实验结果，如图5和图6所示。就实验结果来说，实验在室内室外的条件下效果差别不显著，(c1)算法校正数值略有偏差，只展现了中心部分，并且四周边缘还是看得出扭曲程度较大，而文中算法虽然也存在校正数值偏差问题，但将扭曲部分校正的效果比较好，弥补了(c1)中校正不足这一点；(d1)虽然将球形全景图全部展开成平面，但是分为上下左右前后六部分进行校正后再拼合，并没有形成整体校正，这不利于后期图像处理工作的进行，而文中算法直接将球形图像以矩形形式展开成平面，弥补了(d1)中的不足。总体上来看，该算法比其他两种算法更适用于将球形全景图像展开成平面，但是不足之处还会在后期的工作中改进，后期的工作中将对球形全景图如何能完整地展现出校正效果进行优化。实验与两种球形校正方法进行了比较，如表1所示，在与球形图坐标算法的比较中，本实验校正效果扭曲程度降低，建立映射关系的时间对比上减少1.22 s，校正用时增加0.39 s；在与球形图立体纹理映射法(sky box)的比较中，实验为整张球形图的校正，而球形图立体纹理映射法(sky box)的校正为分开的六张图的校正再合为一张图的校正，实验建立映射关系的时间对比上减少2.11 s，校正用时减少0.66 s。总之，改进的算法产生了更好的输出。在球形图像校正的过程中利用改进的经纬映射和透视投影算法进行校正，有效地利用了算法的低复杂度处理思想，虽然相对于经纬映射和透视投影算法的改进并不大，但改进的算法可以实现更好的校正结果，同时在建立映射关系上所花费的时间最少。

图5 室内图测试

图6 室外图测试

表1 不同算法测试实验时间对比

从表1可以看出，文中算法应用于球形图像展开成平面图时，所需建立映射关系用时最少，而校正所用时间与其他两种算法相当，所以文中算法可用于将球形全景图展开成平面。

文中做了相关图像质量评价，实验数据为自己拍摄的球形图，文中算法将球形图校正为平面图，为了评价校正图像结果，另外拍摄了一组原场景平面图，如图7所示。

图7 图像质量评价实验数据图

图校正图像的质量评价方法由信息熵和均方根误差来表示。信息熵的表达公式为：

(9)

其中，L表示图像灰度级别，pi表示灰度值i像素占总像素的比例，E越大表示参考图像与所校正图像相似度越高。均方根误差的表达公式为：

(10)

其中，R(xi,yj)为参考图像像素，F(xi,yj)为校正图像像素，m*n为图像大小，RMSE越小，表示参考图像与校正图像差异越小。图像质量评价结果如表2所示。

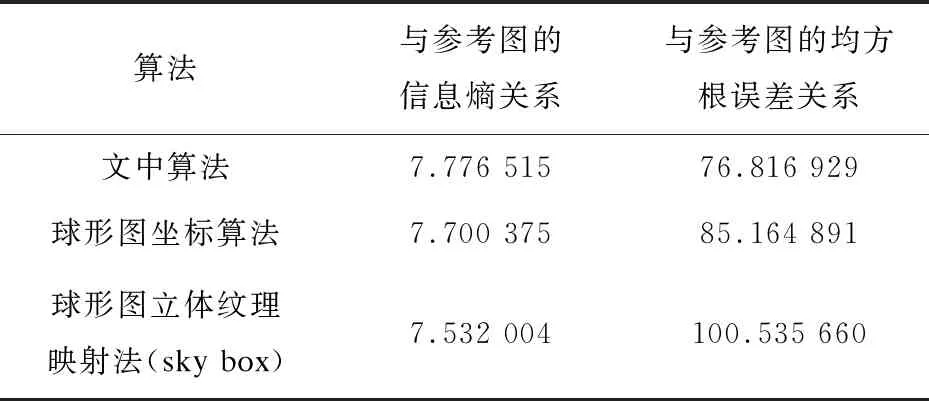
表2 图像质量评价实验结果

从表2可以看出，文中算法的校正结果与参考图的信息熵最大，与参考图的均方根误差值最小，表明文中算法的校正结果略优于球形图坐标算法和球形图立体纹理映射法(sky box)。

4 结束语

提出了一种校正球形全景图的方法：结合改进的经纬映射算法及改进的球面透视投影算法，得到了球形全景图展开成平面的方法。与依赖单纯的坐标和纹理映射来构建类似球形图校正的现有方法不同，该方法利用改进的经纬映射算法及改进的球面透视投影算法来校正球形图。从多组室内室外的实验球形图中选出一组图来展示，经实验结果看，该算法实现效果比其他两种算法的实现效果更好一些，扭曲程度得到一定程度的改善，在建立映射关系方面所用时间最少，在校正方面所用时间相差无几。但是由于没有精确地计算球形全景图的视角大小，最终纠正的效果还有不足之处，球形图像最终映射成平面图时有些地方并没有完全显示出来，所以接下来的工作是要不断完善映射的成果，力求增加其完整性。此外该球形图的校正算法可以进一步优化，以满足实时或时间要求苛刻的应用。