基于结构方程模型的雨天城市公交路段延误影响因素分析

吴 中，吴季恒，吴 琼，杨海飞

(河海大学 土木与交通学院，江苏 南京 210098)

降雨作为一种常见的天气条件，会直接造成路面溜滑、视线受阻、行车不安全因素增加，已经成为恶化道路条件、降低交通运行效率、加剧交通拥堵的重要环境因素。而城市道路具有交通量大且时空分布特性分明、城市道路等级多、瓶颈节点多、交叉口交通运行模式复杂等特点，道路行车容易受到降雨天气的不利影响。

从20世纪50年代开始，国外的学者[1]认识到降雨等不良天气会对道路交通运行产生严重影响。最初的研究主要集中在降雨对宏观道路运行特性的影响，如降雨会导致路段通行能力、交通量、交叉口饱和流率、运行速度等参数[2-4]下降，降雨还会影响出行量和出行空间分布[5]等。学者利用多层线性回归、神经网络等数据拟合方法建立了一系列雨天交通预测模型，如雨天通行能力计算模型[6-7]、雨天速度预测模型[8]、雨天交通流模型[9]、雨天拥堵预测模型[10]等。这类研究大多从整体出发，将实测数据的变化归咎于降雨单一因素，忽视了因下雨而诱发的其它因素影响以及因素之间的相互影响。

随着研究的深入，更多的因素开始纳入研究范围。研究发现降雨会增加驾驶员压力，导致驾驶行为发生改变，还会降低车速、增大车头时距[11]等。祝会兵[12]、颜冉[13]等考虑雨天驾驶行为改变对传统的交通模型进行改进，提出了一系列缓解雨天城市干道拥堵问题的措施。龚大鹏[14]研究了降雨时等级道路、运行时段、拥堵程度、是否处于交通高峰期等因素对交通运行的影响，得到一些相关成果与结论。许方经[15]通过分析确定雨天城市道路通行能力的影响因素包括降雨强度、能见度和车道净宽，建立了雨天通行能力计算模型。李秋萍[16]运用多元线性回归模型分析了降雨量、道路等级、车流量、晴天同时段对照车速等因素在速度下降和速度上升两类道路上的作用差异。

本文的研究对象为雨天城市道路，主要研究道路路段基本特征、交通管理与控制措施、环境条件等各类因素对城市道路公交运行的综合作用；选取行程车速作为反映公交车路段运行状态的指标，考虑多个因素共同作用，建立了雨天路段车速的结构方程模型；通过量化路段模型分析，得到模型各变量间的路径系数，判断不同影响因素对雨天城市道路交通运行的定向效应，分析不同因素的影响程度和内在关系。

1 公交数据及其特征

1.1 公交数据

路段作为城市道路网络的主要组成部分，交通整体运行效率受到路段的制约和影响。公交车运行具有固定的运行路线、运行距离和运行起讫点，是有较好规律性的研究对象。以佛山公交126路作为研究对象，数据选取时间为2019年8月至9月。佛山公交126路由禅城区中心医院站至鲤鱼沙站，全程17.32 km，整条线路存在多种形式的路段。结合各站点间的实际情况，选取丽日豪庭-惠景城(二级双向6车道)、劳动力市场-华远东路口(一级双向6车道)、华远东路口-山水居(一级双向6车道)、市一医院A-禅城区政府(二级双向8车道)、通济桥-儿童活动中心(一级双向4车道)、儿童活动中心-普澜一路(一级双向4车道)、祖庙路-祖庙A(一级双向4车道)、人民西-佛山中医院A(一级双向6车道)、河畔明珠-中山桥(一级双向2车道)等九个路段作为研究对象。

原始数据利用车载全球定位系统(global positioning system，GPS)记录仪记录，包括车牌号、GPS时间、服务器时间、经度、纬度、速度(km/h)和方向。公交到站时GPS反馈的经纬度保持不变，从而可以得到各个站点的时刻表，通过时刻表可以得到各站点间的行程时间和行程车速。

此外，佛山公交126路公交线路靠近佛山市南海区气象局，公交行车路线上的降雨量数据直接参考佛山市南海区的降雨量数据。

1.2 数据特征

经过筛选得到144趟工作日行车数据，包括上行82趟，下行62趟，其中高峰时段样本占比约29%，夜晚样本占比约26%，晴天占比77.2%，雨天占比22.8%。获取的公交数据按照晴天-雨天，高峰-平峰进行组合分组，并对四组数据采用K-S检验，每组数据的渐进显著性水平均为0.2(大于0.05)，可以认为每组数据均符合正态分布。画出每一类数据的行程速度频数分布直方图，并采取正态分布进行拟合可以得到图1，相关统计参数如表1所示。

图1 行程速度分布图

从表1中的数据发现，四类车辆的平均行程车速从大到小分别为：晴天平峰、雨天平峰、晴天高峰、雨天高峰；平峰时段运行车速大于高峰时段运行车速，晴天运行车速大于雨天运行车速的趋势，与正常规律相符。同处于平峰(高峰)时，晴天、雨天运行速度差距较小；同处于晴天(雨天)时，高峰、平峰运行速度差距较大。数据显示出较强的合理性。

表1 行程速度数据统计参数表

2 结构方程模型

2.1 初始模型

结构方程模型是基于变量的协方差矩阵来分析变量之间关系的统计方法。模型中既包含可以直接测量的观察变量，也包含与观测变量有关但无法直接测量的潜在变量，能够较好地分析潜变量对总体的作用及潜变量之间的关系。结构方程方法也适合于分析雨天路段交通特性的影响因子。

根据经验，本文从道路基本特征、交通管理与控制措施、环境条件三方面确定了各影响因素及其对应的观测指标，形成了路段结构方程模型变量表，如表2所示，包括3个潜变量和13个观察变量。选取行程速度作为反映公交车路段运行状态的指标。

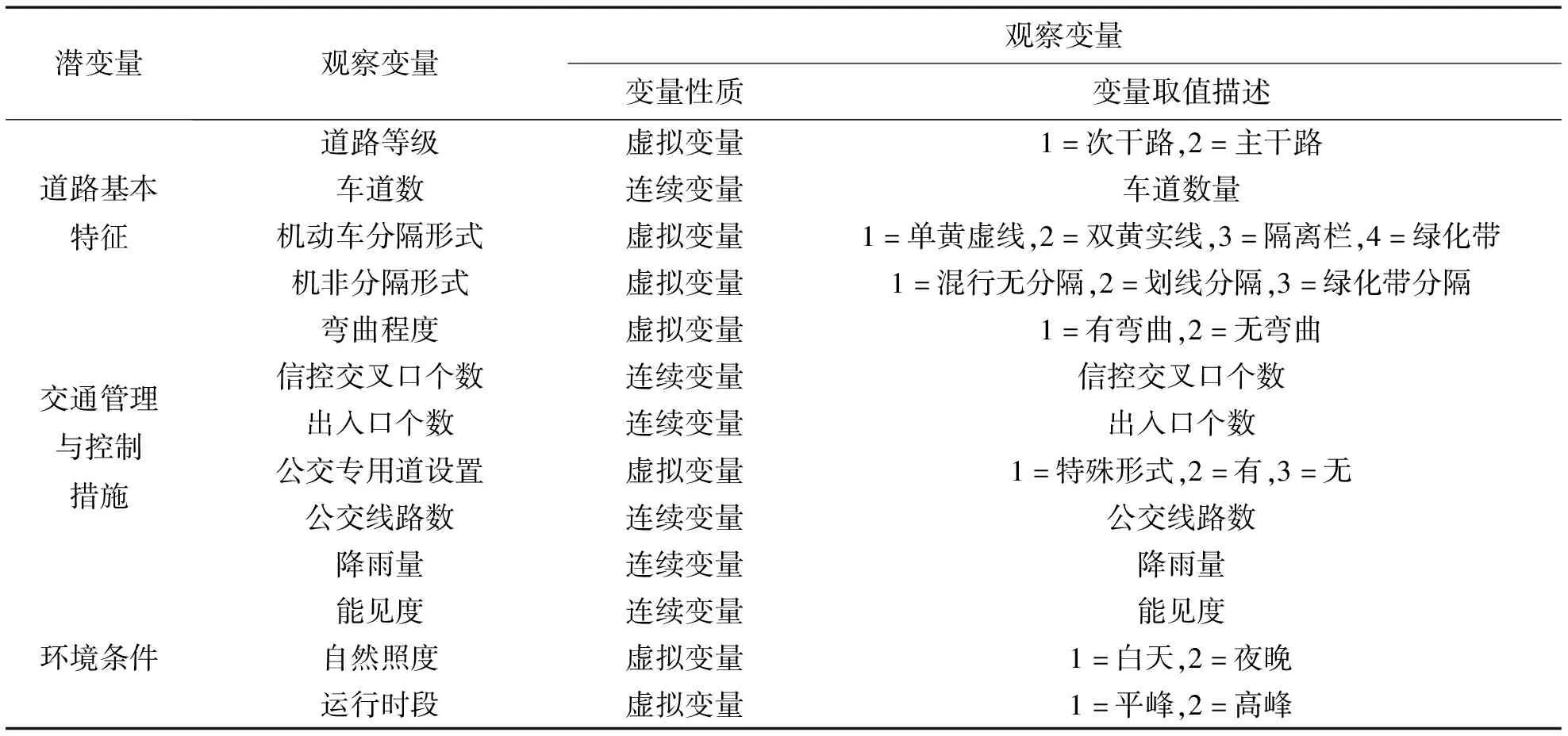
表2 路段结构方程初设模型变量表

初始模型相关关系的逻辑图如图2所示。在计算结构方程模型的矩结构分析(analysis of moment structures，AMOS)软件平台中，观察变量用长方形或正方形表示，潜变量用椭圆或圆表示，单向箭头表示单向因果关系，双箭头表示两个变量互为因果关系。模型各变量的测量误差用ei表示，且测量误差间不独立。模型可以采用极大似然估计法估算求解。由于初始模型完全凭经验主观建立，模型仍需要按一定规则和相关指标进行修正，以更加客观地表达各种变量之间的相互影响的逻辑结构关系。

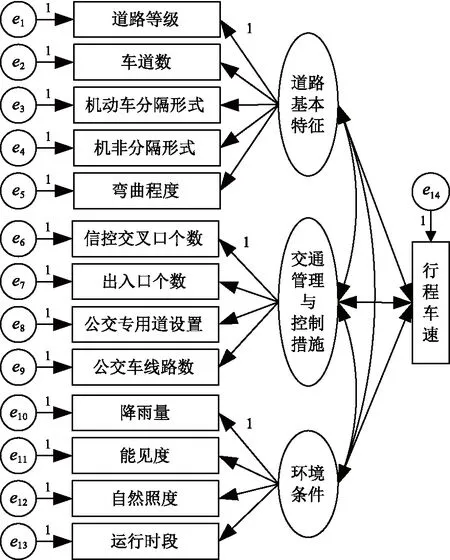
图2 路段结构方程模型路径图

2.2 模型修正依据

验证性因素分析能够检验观察变量和对应潜变量之间的关系是否正确，是模型分析与修正的基础。因素负荷量(路径系数)分为非标准化因素负荷量和标准化因素负荷量。非标准化因素负荷量表示自变量变化一个单位时，因变量的实际变化值，因而非标准化因素负荷量可以用于检验模型估计是否显著；标准化因素负荷量是非标准化因素负荷量除以标准差得到的统一量纲值，其取值在-1～1之间，能够直接进行不同系数对比，绝对值越大说明自变量对因变量的相对重要程度越大。验证性因素分析需满足的条件如下：

(1)临界比(critical ration,RC)是结构方程非标准化因素负荷量显著性检验条件的重要指标，相当于t检验中的t值。临界比大于1.96，表示参数估计值达到了0.05的显著水平，即P小于0.05。

(2)标准化因素负荷量λ在理想条件下要大于0.7，在模型修正和进行模型逻辑结构探索分析时至少要大于0.5。

(3)组成信度(composite reliability,CR)是检验潜在变量的信度指标，是衡量模型内在质量的标准之一。组成信度的理想范围为0.6～0.95，计算公式如下(1)式。其中，θ为观察变量的测量误差值。

(1)

(4)平均方差萃取量(average variance extracted,Ave)用于衡量潜在构念所解释的变异量有多少来自测量误差，其数值越大，说明来自测量误差的变异量越小，观察变量越能有效的反映对应的潜变量的特性。平均方差萃取量是一种模型收敛效度的指标，一般的判别标准要大于0.5。平均方差萃取量的计算公式如下(2)式：

(2)

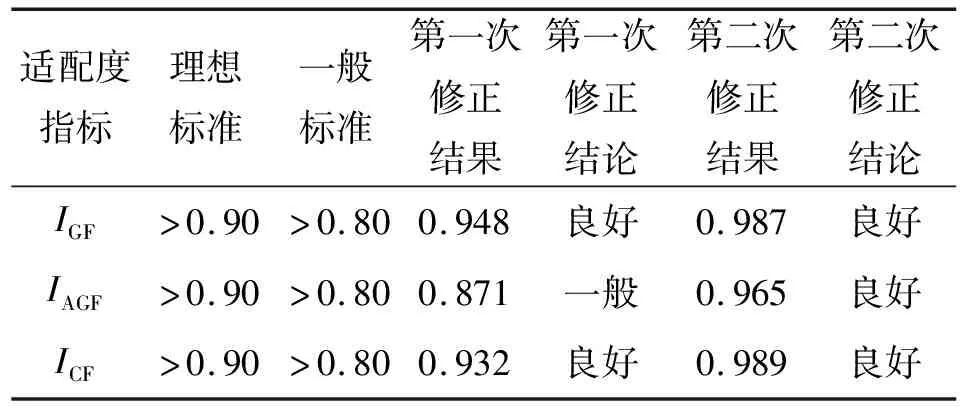
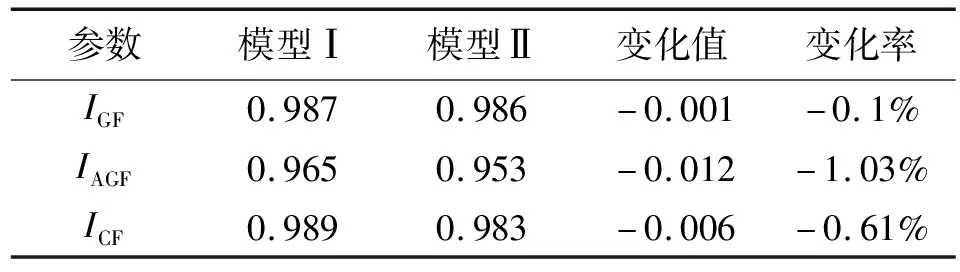
对模型期望协方差矩阵和样本协方差矩阵的差异由适配度指标进行评估，它是理论结构模型对实际数据拟合程度的统计指标。由于数学方法不同，结构方程模型常用的适配度指标有很多。本模型选取适配度指数(goodness-of-fit index，GFI)、调整后适配度指数(adjusted goodness-of-fit index AGFI)和比较适配指数(comparative fit index，CFI)等三个指标作为模型的评价指标。一般认为IGF>0.9、IAGF>0.9、ICF>0.9时模型达到理想标准，0.8

2.3 修正模型

由数据进行初始模型验证性分析，所有观察变量的非标准化因素负荷量均满足显著性检验条件(RC>1.96，P<0.05)，变量弯曲程度、公交车线路数、能见度的标准化因素负荷量均小于0.5，将这三个观察变量删除后再次进行验证性因素分析。修正后临界比值RC均大于1.96，P值均小于0.001，满足显著性条件，标准化因素负荷量均大于0.5，符合要求，具体计算值如表3所示。

根据标准化因素负荷量分别计算各潜变量的组成信度值CR和平均方差萃取量AVE，由表3可知，三个潜变量的组成信度CR均在0.6～0.95之间，平均方差萃取量AVE均大于0.5，满足验证性因素分析的要求。拟合后，初始模型中的测量模型对应的适配度指标IGF=0.885，IAGF=0.803，ICF=0.841仅达到一般指标。根据AMOS提供的修正指数IMI来释放部分限制路径、增添一些新路径来提高模型拟合度(IMI值表示将原本受限制的参数改为容许自由估计后，整个模型改良时将会减少的最小卡方值)。

表3 修正后测量模型因素负荷量表

(1)第一次修正过程

删除道路基本特征下的机非分隔形式这一观察变量；将道路等级测量误差项e1和公交专用道设置测量误差项e8设置为相关关系；将车道数测量误差项e2和机动车分隔形式测量误差项e3设置为相关关系；将车道数测量误差项e2和公交专用道设置测量误差项e8设置为相关关系；将机动车分隔形式测量误差项e3和信控交叉口个数测量误差项e6设置为相关关系；将机动车分隔形式测量误差项e3和出入口个数测量误差项e7设置为相关关系；将机动车分隔形式测量误差项e3和公交专用道设置测量误差项e8设置为相关关系。

第一次修正后，适配度指标IGF和ICF的拟合结果均大于0.9，IAGF拟合结果小于0.9，模型仍不够理想。

(2)第二次修正过程

将道路等级测量误差项e1和出入口个数测量误差项e7设置为相关关系；将车道数测量误差项e2和出入口个数测量误差项e7设置为相关关系。

两次修正后的模型称为模型Ⅰ，其适配度指标拟合结果见表4，模型Ⅰ适配度指标IGF、ICF、IAGF的拟合结果均大于0.9，达到理想标准。说明模型Ⅰ与实际数据之间契合度有较大提高，模型结果有说服力。模型Ⅰ对应的标准路径系数图如图3所示(注：“***”表示P<0.001,SE为估计参数的标准误)。

表4 模型Ⅰ适配度指标拟合结果

3 单一因素模型对比

如果不考虑环境条件下自然照度和运行时间两个影响因素，仅研究降雨这一单一变量对行程速度的影响，可以建立对比模型Ⅱ。模型Ⅱ重复检验、修正、运算后得到的路段结构方程模型标准路径系数如图4所示。

图4 模型Ⅱ标准路径系数图

表5对比表明，模型Ⅰ的适配度指标高于模型Ⅱ，即模型Ⅰ与实际数据的拟合度更高。模型Ⅰ中降雨量对行程车速的路径系数为-0.17，模型Ⅱ路径系数为-0.13，模型Ⅱ仅为模型Ⅰ的76.5%，表明仅考虑降雨量而忽视其他环境因素的相互作用及对运行车速的共同影响，这会使得由降雨诱发的影响行程车速的其他边际效应被低估或被忽略。

表5 模型Ⅰ及模型Ⅱ对比表

4 模型路径分析

4.1 运行速度路径系数

对模型Ⅰ(图3)中的结果进行整理，观察变量影响潜变量的路径系数称为一级效应，潜变量影响评价指标(运行车速)的路径系数称为二级效应，综合效应为一级效应、二级效应乘积，绝对值反映观测变量影响公交车雨天行驶速度的权重关系，正负表示观测变量和因变量的变化方向是否相同。模型Ⅰ各影响因素效应如表6所示。

图3 模型Ⅰ标准路径系数图

4.2 影响机理

由表6可知，在三类影响因素中，环境条件对公交行程车速的影响最大，交通管理与控制措施的影响次之，道路基本特征的影响最小，其影响系数为分别为-0.298、-0.222、0.080。道路基本特征包含三个变量，且影响均为正向的，即道路等级越高、车道数越多、采取更有力的双向车流分离形式会使得行程车速提高。交通管理与控制措施的三个观测变量影响均为负向，即出入口个数越多、信控交叉口个数越多、未设置公交专用道会使得行程车速降低。环境条件中降雨量、自然照度和运行时段三个变量影响均为负向，降雨量越多、自然照度越低的夜晚、运行越接近高峰时段会使得行程车速降低。

表6 各影响因素综合效应表

9个观测变量对行程车速的影响可分为三类:(1)综合效应大于0.2的影响较大变量：运行时段(-0.270)、自然照度(-0.239)。(2)综合效应在0.1～0.2之间的变量：出入口个数(-0.175)、降雨量(-0.170)、信控交叉口个数(-0.164)、公交专用道设置(-0.141)。(3)综合效应小于0.1的影响较小变量：道路等级(0.066)、车道数(0.063)、机动车分隔形式(0.053)。

从模型观测变量的综合效应看，降雨量并不是影响公交行驶速度的最主要因素，而运行时段、自然照度、出入口个数对行车速度的影响更大。这表明雨天对城市公交运行的影响是通过雨天诱发其他条件劣化或是降雨因素与其他因素共同作用完成的。城市道路车辆运行的某些瓶颈条件在降雨作用下会更加制约交通的运行。某些对交通影响不大的因素，虽然有降雨的作用，对城市车辆运行的阻碍作用仍不显著。

天气正常时，高峰期城市道路会发生拥堵表明高峰时段道路通行能力已经制约了交通运行，若雨天与高峰期叠加会使得这种阻碍作用更加显著。由此可以看出雨天会使大部分阻碍因素更加突显，解决城市雨天交通阻塞应该从那些突显的主要因素入手，通过硬件设施建设和管理措施的综合治理起到缓解雨天交通拥堵的作用。

5 结语

本文应用结构方程模型和实际调查数据得到不同降雨强度下城市干道基本路段影响公交运行的显著影响因素，分析了城市交通路段延误产生原因及降雨对公交运行的影响，确定了影响城市道路公交运行因素间的逻辑关系，解释了雨天城市交通拥堵或延误的机理，宏观交通流的影响因素的影响权重表达在模型图3中。研究结果表明，交通高峰期和夜晚工况下雨天对城市公交运营的影响最大。

从分析结果看，平峰期降雨对公交的影响很小甚至没有影响，为减少高峰期降雨对城市道路的影响，城市应多设置公交专用道，减少信号灯数量或设置信号灯公交优先，对公交线路上的出入口(包括人行横道)进行管制。在城市宏观交通管理上应注重交通流的空间均衡、削减高峰时段交通流峰值、实行瓶颈路段交通分流、改变雨天信号灯控制方案等，降低雨天道路环境控制因素对行车速度的影响。

本文是针对公交车进行研究的，但研究结论和雨天影响交通的基本特性对其他车辆雨天运行也有参考价值。