电-磁-弹功能梯度板中的波动瞬态响应分析

谢根全，宋鑫朋

(湖南科技大学 土木工程学院，湖南 湘潭 411201)

磁电多场耦合的理论研究可追溯到上世纪50年代。至今，国内外在压电、压磁等功能材料结构的材料性能和力学性质方面进行了一系列的研究，尤其在理论研究方面取得了重要进展。在电-磁-弹材料结构的动力学性能研究方面：KALISKI[1]推导出热-电-磁-弹的波动方程；文献[2-12]对压电-压磁层合板或功能梯度材料板和壳中波的传播特性(弥散特性、特征波面、相速度和群速度)进行了研究。在波动瞬态响应方面的研究：HOU等[13]，WANG等[14]推导并分析了多铁空心圆柱在轴对称平面应变变形下的瞬态响应；DAGA等[15]应用四节点Runge-Kutta法的半解析有限单元法研究了磁-电-弹三相材料组成的简支层合圆柱壳的瞬态响应，对弹性圆柱壳和电-磁-弹耦合的圆柱壳的计算结果进行了比较；WANG等[16]借助商业软件Abaqus建立了多铁复合材料结构的三维有限元模型，使用直接时间积分法对双层多铁复合材料中波动瞬态响应进行了计算。

求功能梯度材料中的波动响应的混合数值法首先由LIU等[17]提出,并在板、壳结构中的波动力学研究中得到各国广泛应用[18-20]。混合数值法的基本思想是在材料梯度变化的方向划分层单元，在垂直梯度方向应用解析法。划分单元的目的主要是对材料参数的变化进行近似并不是对位移进行近似，因此，其解具有很高的精度。磁电弹性功能梯度材料结构不仅材料参数梯度变化，而且存在多场耦合。对于有些材料参数变化梯度的结构，要获得结构中波动瞬态响应的解析解很困难;混合数值法比有限元法求解具有高效性，因为其单元数远少于有限元法的单元数。对于反问题来说，因为要反复调用正问题，正问题求解的高效性显得尤为重要，因此用混合数值法求解具有优越性。

本文假设电-磁-弹(electric-magneto-elastic，EME)板材料参数在厚度方向呈二次梯度变化,应用能量变分原理和层单元法建立板的动力学微分非常方程,用傅立叶变换、反傅立叶变换方法和模态叠加法获得板在力激励和电极激励下的波动瞬态响应,研究磁电参数对电磁弹板中的波动瞬态响应的影响。

1 理论模型

1.1 基本方程

如图1所示，板厚为h的无限大电磁功能梯度材料板，在厚度方向上划分上、中、下三个节面。

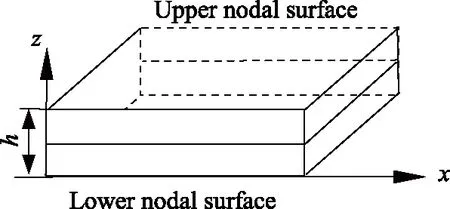
图1 电磁功能梯度材料板的单元模型

设各层材料为各向异性材料，电-磁-弹材料板的本构关系[10]为

(1)

式中：σ为应力向量；C为弹性系数矩阵；ε为应变向量；E为电场强度向量；H为磁场强度向量；D为电位移向量；B为磁感强度(磁流密度)向量；e,q,g,α,μ分别为压电系数、压磁系数、介电常数、磁电效应系数、磁导率矩阵。

压电-压磁-弹性板的广义几何方程为

(2)

式中：u1,u2,u3分别为x,y,z方向的弹性位移分量u,v,w；φ，ψ分别为电势函数、磁势函数，下标中的逗号表示求导(偏导)。

将压电-压磁板沿厚度方向划分为上、中、下三个节面，板内的位移、电势、磁势分别用形函数和节面位移、电势、磁势表示，即

(3)

式中：下标k为层数编号，1为底层，3为顶层；形函数Nk(z)为

(4)

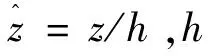
假设材料按二次抛物线规律

(5)

式中：p为弹性参数；上标u、l分别表示单元层的上层和下层。

1.2 控制方程

压电-压磁-弹性板的能量泛函为

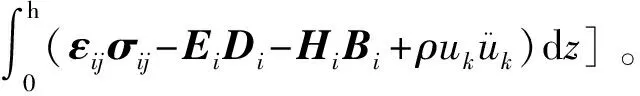
(6)

式中：Fi为施加在第i节面上的力；Di3是第i节面上沿z轴向的电位移向量，Bi3是第i节面上沿z轴向的磁感强度向量,ρ为质量密度。

对能量泛函变分δΠ=0,得到

(7)

其中：

(8)

(9)

(10)

(11)

式中：0为零矩阵；I为三维单位矩阵。AD为如下微分算子[11]

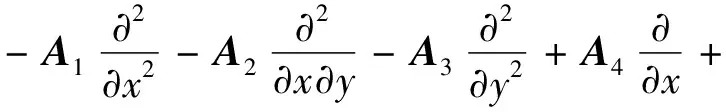
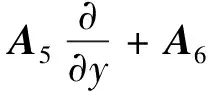
(12)

CD,QD,GD,RD,YD参照式(12)计算，其中Ai,Ci,Qi,Gi,Ri,Yi的表达式见附录A。

引入如下的傅里叶变换:

(13)

式中：kx为x方向的波数；ky为y方向的波数。

对式(7)施加傅里叶变换得

(14)

其中：

(15)

C、Q、G、Y、R参照A计算，其中Ai,Ci,Qi,Gi,Yi,Ri的表达式见附录A。

为了获得力载荷激励下的位移和静电势、静磁势响应，假设

(16)

为了获得电极激励下的位移和静电势、静磁势响应，假设

F=0,φi=φe,Bz=0。

(17)

1.3 瞬态响应分析

对式(14)降维，可以变换为

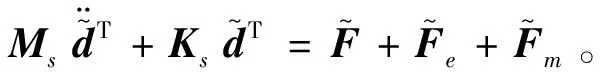
(18)

式中右边三项分别为力载荷、等效电极载荷和等效磁极载荷的傅里叶变换。

(19)

(20)

Ks=A+CE-1Σ+QX-1Γ，

(21)

其中：

X=R-TY-G-1R，

(22)

(23)

Σ=R-1CT+Y-1QT，

(24)

E=R-1G-Y-1RT。

(25)

对于整数个电极和磁极激励，假设电极、磁极反对称分布在y轴上，电势、磁势的傅里叶变换分别为[21]

(26)

(27)

式中：p0为静电势常数；he为电极宽度；Ne为电极总数；de为两个电极间的距离；m0为静磁势常数；hm为磁极宽度；Nm为磁极总数；dm为两个磁极间的距离。

在计算时，对以下参数进行无量纲化：

式中：t0是剪切波横穿板厚的时间；c0为电磁材料中剪切波的速度；ρ0,c66分别为电磁材料的密度和弹性的参考值；es=1 C/m2；gs=10-10F/m；c66=1 GPa；ρ0=1 kg/m3；f0=1 N/m2；qs=1 Vs/m2；μs=10-6Vs/Am；αs=10-12Ns/Vm。

应用反傅里叶变换得到位移和静电势、静磁势响应

(28)

φ=E-1Σd，

(29)

ψ=X-1Γd。

(30)

2 算例与分析

2.1 算例 施加力荷载

板的厚度h=0.5 m，在板的上表面x=0这根线上施加一个阶跃载荷F=q0δ(x)H(t)，q0=1 kN,H(t)为单位阶跃函数。

傅里叶变换波数域内的位移响应为

(31)

一维反傅里叶变换得到时域内的位移

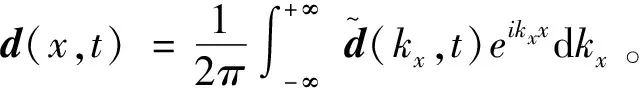
(32)

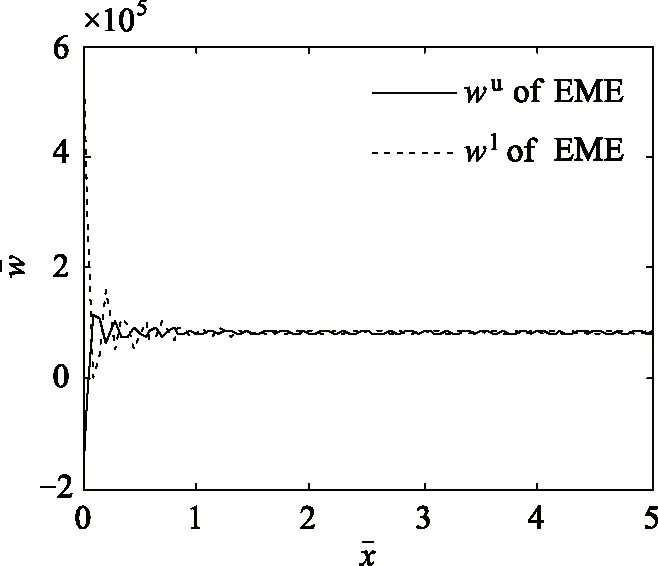
图2 电-磁-弹功能梯度板顶面和底面的位移w沿x轴方向的分布

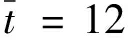
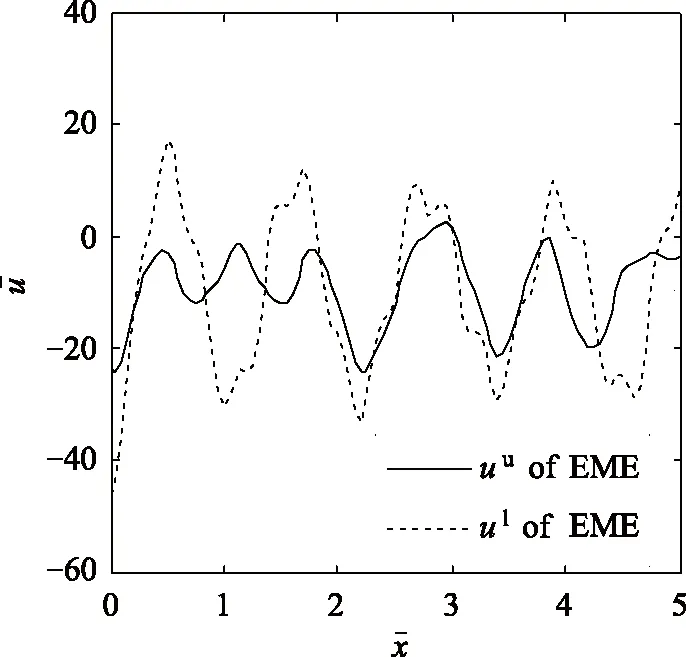
图3 电-磁-弹功能梯度板顶面和底面的位移u沿x轴方向的分布

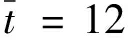
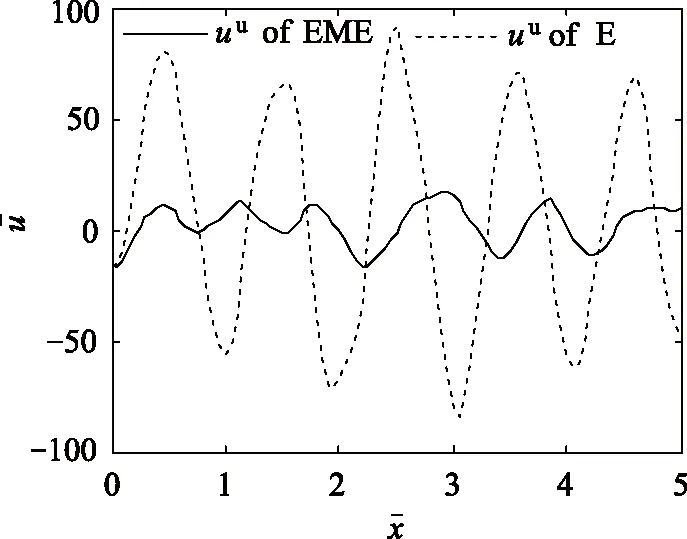
图4 功能梯度弹性板(E)和功能梯度电磁弹性板(EME)顶面位移u沿x轴方向的分布

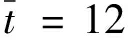
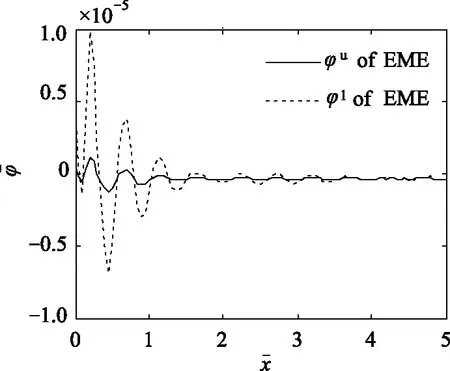
图5 电-磁-弹功能梯度板顶面和底面的电势φ沿x轴方向的分布

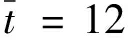
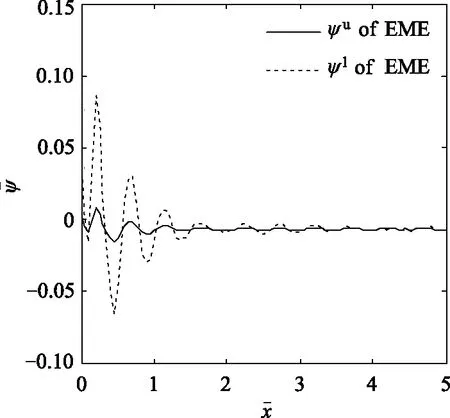
图6 电-磁-弹功能梯度板顶面和底面的磁势ψ沿x轴方向的分布

2.2 算例 施加电极激励

在x=0线上反对称布置Ne=10个电极对，电极宽度he=0.01 m，电极间距de=0.05 m，静电势常数p0=10 V，大数α=1015。

电极激励的等效载荷为

(33)

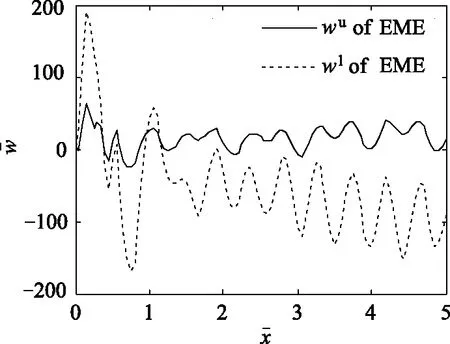
图7 电极激励下，电-磁-弹功能梯度板顶面和底面的位移w 沿x轴方向的分布

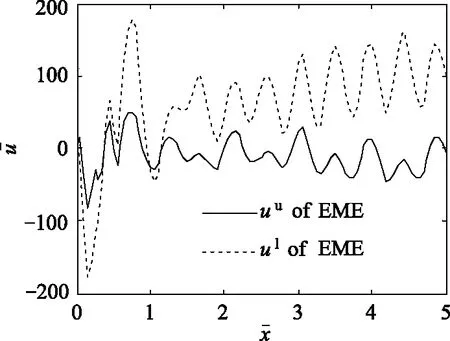
图8 电极激励下，电-磁-弹功能梯度板顶面和底面的位移u沿x轴方向的分布

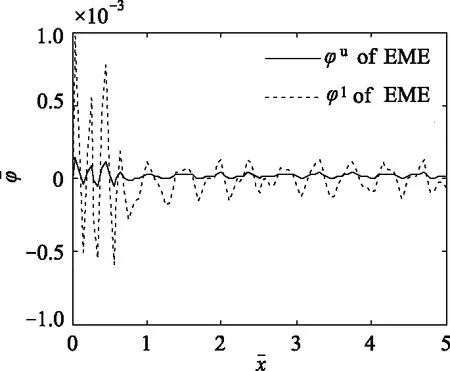
图9 电极激励下，电-磁-弹功能梯度板顶面和底面的电势φ沿x轴方向的分布

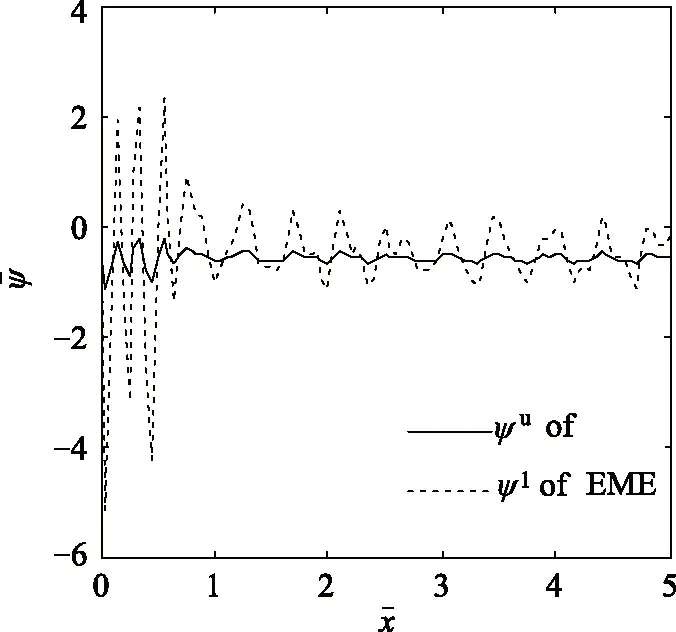
图10 电极激励下，电-磁-弹功能梯度板顶面和底面的磁势ψ沿x轴方向的分布

3 结论

应用混合数值法研究电-磁-弹功能梯度材料板中波动瞬态响应。分别在板的x=0直线上施加力和电极激励，应用混合数值法获得了电-磁-弹功能梯度材料板的上、下表面的弹性波动响应和电势、磁势响应，得出如下结论：

(1)在力激励下，电-磁-弹功能梯度材料板中的横波w的波幅沿梯度增大的方向减小，在厚度方向是拉伸波。

(2)在力激励下，电-磁-弹功能梯度材料板中的纵波u的波幅沿梯度增大的方向减小。

(3)在力激励下，电-磁-弹功能梯度材料板中的电势和磁势的幅值沿梯度增大的方向减小。

(4)在电极激励下，电-磁-弹功能梯度材料板中的纵波u的波幅沿梯度增大的方向减小。

(5)在电极激励下，电-磁-弹功能梯度材料板中的电势和磁势的幅值沿梯度增大的方向减小。

(6)在力激励下，磁势响应与电势响应的波形相似，只是波幅大小不一样；但在电极激励下，磁势响应与电势响应的波形存在差异。

附录A

下面各表达式中的上标u、l分别表示单元层的上层和下层。

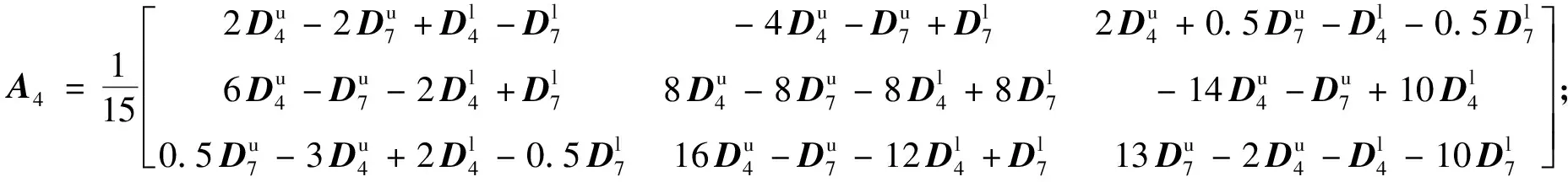
只要将e改为q，Qi的表达式和Ci一样；只要将g改为μ、α，Yi、Ri的表达式和Gi一样。

附录B

下层磁电材料参数如下：

上层材料参数为下层的1.5倍。