Klein瓶的一种简单生成方法

赵姣珍，许道云

(1.贵州民族大学人文科技学院 大数据与信息工程学院，贵州 贵阳 550025；2.贵州大学 计算机科学与技术学院，贵州 贵阳 550025)

2020年，两位数学家Joshua Evan Greene和Andrew Lobb解决了一个百年未解的数学难题——平面闭环上内接矩形问题[1-2]，问题的最终解决与莫比乌斯带和克莱因瓶嵌入到四维空间密切相关。所谓的内接矩形问题是指：对于平面上任何简单闭曲线(闭环)，对任意给定的比值r，是否存在环上的4个点，以此形成的矩形其长宽比为r？问题于1911年提出，看似简单，其实解决起来困难。2019年，著名华人数学家陶哲轩用积分方法证明了内接矩形是正方形时结论成立[3]，其论文长达49页。

早在1977年，数学家Herbert Vaughan在解决该问题时曾经引入一种方法[2]：将矩形表示转化为两条“长度相等、中点重合”线段。这两条线段就是矩形的对角线，对于一条线段AB，取中点坐标为(x,y)，线段长度为d，可以编码AB到三维空间中的一个点(x,y,d)。Herbert Vaughan发现，如果在曲线上按每一对点并对其进行绘制，得到一个令人惊讶的形状——Mobius带。

对于一条线段AB的编码，进一步考虑线段AB与X轴正向的夹角α。于是，平面上的一条线段AB可以编码到四维空间中的一个点(x,y,d,α)。2019年，C.Hugelmeyer运用Mobius带嵌入到四维空间的方法证明了至少对1/3的长宽比值，问题的结论成立[4]。

Joshua Evan Greene和Andrew Lobb再次利用Herbert Vaughan的方法，运用Mobius带嵌入到四维辛空间，最终解决了这个百年未解的数学难题[5]，其论文一共只有6页。当他们把证明结果发表出来时，布朗大学数学家Richard Schwartz赞叹[2]：万万没想到，解决此问题的正确方式是这样的！

本文基于Herbert Vaughan的思路和方法，给出Klein瓶的一种简单生成方法。

1 基本原理

基于Herbert Vaughan的思路和方法[2]，由平面上一条简单闭曲线C(闭环)和位于闭环C内部的一条简单曲线段L可以构成一条Mobius带(图1)。

图1 环线扫描生成的Mobius带

同一条Mobius带，也可以认为是由曲线段沿环线扫描生成(图2)。

图2 曲线段扫描生成的Mobius带

基于上述原理，由平面上一条简单C闭环和位于闭环C内部的另一条简单闭环C0就可以生成一个Klein瓶。

在图3中，将内环C0切分为两条有向曲线段：AB和BA。两条有向曲线段首尾相接，按图1中的方式，AB和BA分别与外环C生成两条Mobius带。以A、B两点对应生成的环线作为两条Mobius带的“粘合”边沿，从而形成一个Klein瓶。

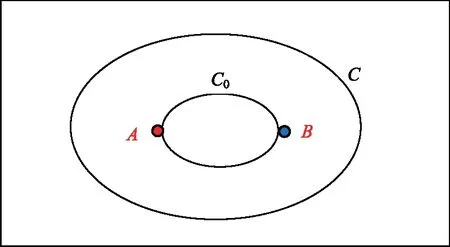
图3 生成Klein瓶的基本部件

2 数学描述

平面上一条连续曲线可以用如下参数方程表示：

x=x(t),y=y(t)(0≤t≤T)，

(1)

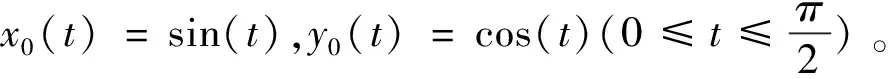
值得注意的是：用参数方程表示曲线时，以参数t从小到大(或从大到小)取值，隐示曲线段具有“方向”。

假定C为平面上一条闭环，L为位于C内部的一条简单曲线，其参数方程分别为

C:x=φ(t),y=ψ(t)(0≤t≤T)；

L:x=φ0(τ),y=ψ0(τ)(0≤τ≤T0)。

(2)

我们先看平面上一个闭环与环内部一点如何形成三维空间中一条闭环。

三维闭环：对于平面上C闭环，以及环内部任意一点P0(a,b)，如下参数方程构成三维空间一条闭环：

(3)

当函数z(t)不是一个常函数时，存在一个平面π，该闭环投影到平面π上有交点。即该闭环在三维空间是简单封闭曲线(图4)，当投影到某个二维空间上后，可能不再是简单闭曲线。

图4 闭环内一点与闭环生成的三维闭环

Mobius带：对于平面上C闭环，以及位于闭环C内部的简单曲线段

L:x=φ0(τ),y=ψ0(τ)(0≤τ≤T0)。

(4)

记简单曲线段起始点(φ0(0),ψ0(0))为A,终止点(φ0(T0),ψ0(T0))为B。动点P(φ0(τ),ψ0(τ))从始点A开始，沿曲线C0连续变动到达终止点B。每个动点P(φ0(t),ψ0(t))与闭环C分别作三维空间一条闭环：

(5)

由此生成一条Mobius带(图5)。

图5 闭环内曲线段与闭环生成的Mobius带

离散化曲线段L参数方程的自变量区间[0,T0]:τ0=0<τ1<…<τn=T0。产生曲线L上离散点P0,P1,…,Pn(Pi=(φ0(τi),ψ0(τi),0≤i≤n)。对应的三维闭环为CP0,CP1,…,CPn。生成的Mobius带可以视为由这样的闭环序列连续(扫描)生成。

3 Klein瓶的生成方法

如图3所示，在平面上给定一个较大闭环C(大环), 在大环C内部给定另一个较小闭环C0(小环)。将小环C0切分为两条有向曲线段：AB和BA。两条有向曲线段首尾相接。

按上述原理，曲线段AB与大环C生成一条Mobius带(左带)；曲线段BA与大环C生成另一条Mobius带(右带)。由A、B两点对应生成的三维环线作为两条Mobius带的“粘合”边沿。于是，由AB和BA分别与C闭环生成的两条Mobius带“粘合”成一个Klein瓶。

从方向上看：由A到B生成左带；由B到A生成右带。以A、B点“粘合”，这相当于动点P在小环C0上从A点出发变动一圈后回到A。

图6中Klein瓶是取圆环生成的，其中：

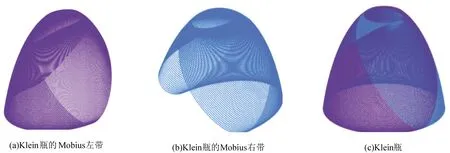
图6 Klein瓶及其Mobius左带和Mobius右带

C:x=2sin(t),y=2cos(t)(0≤t≤2π)；

C0:x=sin(τ),y=cos(τ)(0≤τ≤2π)。

(6)

左带对应单位圆C0的下半部分(曲线)，右带对应单位圆C0的上半部分(曲线)。

4 讨论

本文给出了Klein瓶的一种简单生成方法，其基本原理来源于平面上一个闭环与位于该闭环内的一条曲线段可以生成一条Mobius带。在作三维闭环时，XY平面上的(x,y)坐标是取曲线上的点P到闭环C上的点Q的中点，z-坐标是取P与Q之间的距离。其实，(x,y)坐标可以取P、Q连线上任一个固定比例点λP+(1-λ)Q(0<λ<1)，z-值可以取为P与Q之间的距离d的一个单调非负函数都可以。

其次，两个闭环C与C0之间的关系是取小环C0在大环C内部。其实，C与C0之间的关系还可以取成“相交”“相离”等关系。

相交(图7)：

图7 闭环相交产生的曲面

C0:x2+y2=1，C:(x-1)2+y2=1。

相离(图8)：

图8 闭环相离产生的曲面

C0:x2+y2=1，C:(x-3)2+y2=1。

当然，也可以在三维空间中考虑C与C0，以及不同位置关系，也许对理解某些物理现象有帮助。正如：太阳、地球和月亮的运行轨道、位置关系、引力函数、引力场等。太阳、地球和月亮沿各自轨道运动所产生的引力场所模拟图可参见相关文献。

Mobius带和Klein瓶在拓扑学中是一类简单而有趣的几何类型，作为单侧曲面尚有一些有意思的问题值得研究。如：基于Mobius带和Klein瓶定义函数的曲面积分等。涉及积分，首先得将曲面的表达式弄清楚。本文给出的Mobius带和Klein瓶的生成有助于深入研究这方面的问题。