基于SVM的BLDCM直接转矩和磁链控制研究

李泽宇，王家军

(杭州电子科技大学自动化学院，浙江 杭州 310018)

0 引 言

无刷直流电机(Brushless DC Motor，BLDCM)继承了直流电机控制简单、效率高等优点，同时解决了其机械换相所带来的火花、噪音等问题，在许多行业得以广泛应用[1]。为获得更好的运行性能，文献[2]通过直接转矩控制算法(Direct Torque Control，DTC)实现了对BLDCM电磁转矩和定子磁链的控制，使电机在负载变化时迅速响应，大大提高了电机的动态性能。传统DTC算法在转矩环中采用滞环控制，且使用6个位置固定的电压空间矢量进行电机驱动，换相时易产生较大的转矩脉动[3]。为此，国内外学者对其转矩脉动的抑制进行了大量研究。文献[4]采用二三相导通模式形成12个电压空间矢量对扇区进行细分，转矩脉动抑制能力有所提高，但换相时的脉动仍明显存在。文献[5]在二三相导通控制的基础上，采用优化的分时换向策略，由转矩偏差决定换相时刻和非零电压空间矢量作用时间，一定程度上抑制了转矩脉动，但效果仍不够理想。文献[6]采用三相导通形成的电压空间矢量对换相时非换流相相电流进行稳定控制，达到较好的转矩脉动抑制效果。上述方法均在传统DTC算法基础上进行优化，依然沿用查询开关表来获取电压空间矢量，转矩脉动抑制效果有限。为此，本文将空间矢量调制技术(Space Vector Modulation，SVM)[7-8]引入到传统DTC算法中，使可供选择的电压空间矢量不再局限于固定方向，实现了对电磁转矩和定子磁链的高性能控制，对BLDCM的转矩脉动抑制效果明显，在不同速度段均具有较好的性能表现。

1 BLDCM数学模型

为简化BLDCM数学模型，做如下假设：(1)电机定子绕组三相完全对称；(2)BLDCM转子为表贴式结构，忽略磁路饱和以及电枢反应，假定d，q轴电感值恒定且相等，即Ld=Lq=L；(3)忽略齿槽效应以及转子铁芯磁滞、涡流所带来的损耗。

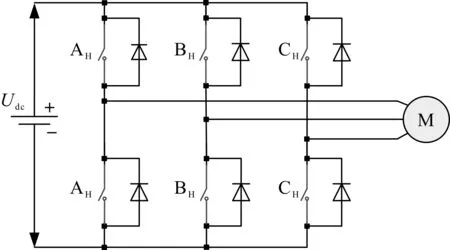
图1 电机与逆变器连接图

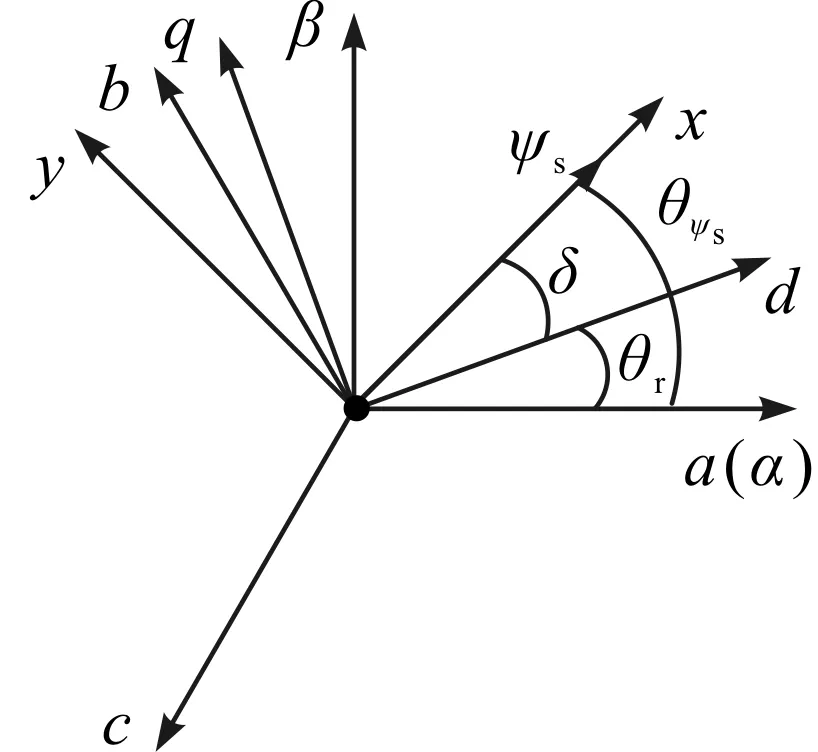
图2 各坐标系位置关系图

基于上述假设，建立的BLDCM在dq坐标系下的数学模型。电压平衡方程为：

(1)

式中，ud，uq分别为定子电压在d，q轴上的分量，R为定子电阻，id，iq分别为定子电流在d，q轴上的分量，Ld，Lq分别为d，q轴电感，ed，eq分别为反电动势在d，q轴上的分量。

定子磁链方程为：

(2)

电磁转矩方程为：

(3)

式中，ω为转子机械转速。

2 基于SVM的直接转矩和磁链控制系统

2.1 定子磁链与电磁转矩计算模块

(4)

式中，pn为转子极对数。

通过定子磁链方程进一步简化式(4)可得：

(5)

本文基于式(2)和式(5)搭建了用于求解电磁转矩和定子磁链的计算模块，其框图结构如图3所示。

图3中，ia，ib，ic，θr分别为实测的定子三相电流以及转子位置角；“^”标注的量均为计算量，f1，f2分别表示定子磁链幅值求解模块和定子磁链位置角求解模块。其中，f1模块中的定子磁链幅值求解函数表示为：

(6)

f2模块中的定子磁链位置角求解函数表示为：

(7)

图3 定子磁链和电磁转矩计算模块框图

2.2 定子磁链与电磁转矩的解耦

本文控制方法的关键在于对定子磁链和电磁转矩进行解耦，实现对两者的独立控制，解耦过程需借助xy坐标系，坐标系位置如图2所示。

BLDCM在xy坐标系下的电压方程为：

(8)

定子磁链矢量ψs位于x轴上，因此不含垂直分量，有：

(9)

通过式(8)和式(9)，可求得定子相电压合成矢量us在xy坐标轴上的分量：

(10)

(11)

式中，ix，iy分别为定子电流在xy坐标轴上的分量。

对于式(11)中的iy，可利用电磁转矩计算公式将其替换。将电磁转矩计算式(4)转换至xy坐标系下，可得：

(12)

(13)

将式(13)代入式(11)，可得：

(14)

2.3 SVM模块

传统DTC算法虽然简单，但控制信号由滞环控制器产生，且只能选择固定方向上的电压空间矢量，极易产生较大的转矩脉动。本文搭建的SVM模块基于空间矢量脉宽调制算法(Space Vector Pulse Width Modulation，SVPWM)，SVPWM算法按照平均值等效原理，在一个开关周期Ts内合理组合多个基本电压空间矢量，可调制出任意方向上的电压空间矢量，从而达到高效控制电磁转矩和定子磁链的目的。

本文采用七段式SVPWM算法[10]，该算法可形成对称的PWM波形，有利于降低谐波分量。算法所使用的6个基本非零电压空间矢量和2个零电压空间矢量均由逆变器产生，其空间分布及所划分的扇区位置如图4所示。各电压空间矢量与逆变器功率开关管状态的对应关系使用3位二进制数表示，其中每位二进制数代表1个桥臂，1表示其上桥臂导通，0表示其下桥臂导通。

以所需电压空间矢量Us位于扇区Ⅰ为例，其合成示意图如图4所示，合成Us的各基本电压空间矢量的施加顺序如图5所示。

图4 基本电压空间矢量以及扇区位置分布

图5 各基本电压空间矢量施加顺序

基于平均值等效原理，图5所示的各电压空间矢量作用时间之间的关系如下：

(15)

式中，T0，T1，T2分别为零电压空间矢量U0和U7、非零电压空间矢量U1、非零电压空间矢量U2在一个开关周期Ts内的作用时间。

图6 基于SVM的BLDCM直接转矩和磁链控制系统框图

3 仿真实验验证与结果分析

根据上述分析并结合图6所示的控制系统框图结构，在MATLAB/Simulink中搭建控制系统的仿真模型，如图7所示。图7中，直流母线电压Udc设置为24 V；速度环PID控制器的参数设置为：kp=1 000，ki=100，kd=0.5；饱和控制器上下限分别设置为0.5和-0.5；BLDCM的参数如表1所示。

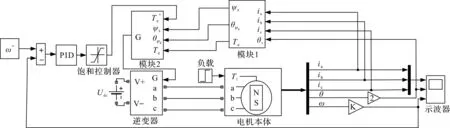
图7 控制系统仿真结构图

表1 电机模型参数表

图7中，模块1为定子磁链和电磁转矩计算模块，其结构如图8所示。

图8 模块1结构图

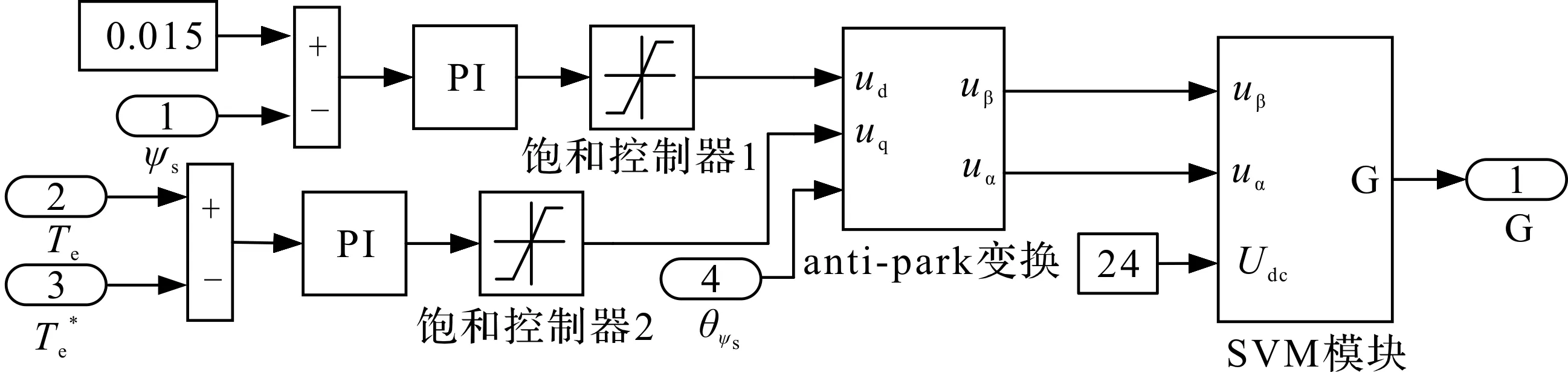
图9 模块2结构图

额定转速为2 500 r/min，带载为0.2 N·m条件下，BLDCM运行所产生的仿真波形如图10所示。从图10可以看出，在基于SVM的BLDCM直接转矩和磁链控制方法下，电机能快速准确地进行速度跟踪，转矩脉动抑制在5%以内，且相电流和定子磁链均无较大脉动。

图10 额定转速下的系统仿真波形

采用本文控制方法，转速分别为30 r/min和1 200 r/min时，进行仿真实验，初始带载均为0.05 N·m。其中，1 200 r/min转速下，在0.03 s时刻负载由0.05N·m增加至0.20 N·m。BLDCM的动态性能及不同转速段的转矩脉动抑制效果仿真波形如图11所示。通过图11可以看出，在较宽的速度范围内，BLDCM均具有良好的转矩脉动抑制效果，并表现出较好的动态性能。

图11 不同转速下的系统仿真波形

4 结束语

传统DTC算法能够加快BLDCM的动态响应速度，但换相时所产生的转矩脉动阻碍了其应用范围。为了弥补该缺陷，本文采用SVM技术对传统DTC算法进行改进，使换相过程变得更加平稳，大大改善了传统控制方法在转矩脉动抑制方面的不足。但是，本文采用的基于SVM的BLDCM直接转矩和磁链控制方法是在转子位置已知情况下实现，接下来将结合无传感技术对该控制方法进一步完善。