无人直升机吊挂系统滑模反步减摆控制

何荣荣，陈 谋，吴庆宪，刘 楠

(南京航空航天大学 自动化学院，南京 210016)

0 引 言

直升机机外吊挂运输一直是军用和民用直升机的重要任务之一，地面设备无法取代其在军事和民用救援领域的作用，而且直升机是在需要垂直起降和悬停能力的作战中最合适的选择[1]。然而,直升机吊挂系统复杂的非线性和动态不稳定性使其难以控制，并且在运输过程中，吊挂负载的振荡是极其危险的，当负载的振荡幅度超过限度时，可能对负载产生损坏甚至威胁到无人直升机的安全[2]。所以直升机吊挂飞行安全问题是目前亟需解决的问题，控制直升机吊挂系统，减小吊挂负载振荡对提高飞行安全十分重要。

目前，国内外对于直升机吊挂的研究主要是对直升机吊挂飞行的空气动力学模型的建立和飞行稳定性的研究和理论分析，无人直升机吊挂系统飞行过程中吊挂负载有效减摆的方法还需进一步研究。文献[2-3]对直升机吊挂系统的稳定性进行分析，并设计了线性纵向模型反步控制器。文献[4]基于CFD方法对CONEX吊挂物进行气动建模，针对直升机吊挂耦合系统操稳特性进行了相关研究，并将模型线性化后设计PID控制器。文献[5]从气动导数和运动模态两个层面分析了直升机吊挂飞行中的耦合。文献[6]建立了直升机吊挂耦合非线性模型，并在小扰动线性化后进行吊挂飞行操纵响应的时域和频域特性分析。文献[7-9]主要对直升机吊挂系统飞行过程中的稳定性和平衡特性进行了分析和研究。尽管无人直升机吊挂系统已有较多的研究成果，但其吊挂子系统全状态非线性鲁棒减摆控制还需进一步研究。

本文将实现无人直升机平面飞行中的有效吊挂减摆控制，受文献[10]的启发，建立直升机刚体吊挂的模型，并且采用反步法解算出减摆的虚拟控制律。参考文献[11]，采用滑模反步和反步的控制方法，对直升机的速度、直升机的姿态角和姿态角速度进行跟踪控制，最终达到无人直升机吊挂非线性系统的减摆跟踪控制效果。

1 无人直升机吊挂动力学模型

本文研究的无人直升机吊挂系统由吊索、吊挂负载等组成，图1所示为其系统组成示意图[12]。其中；oxyz为机体坐标系，其坐标原点o在直升机重心的正下方；ox轴以直升机参考平面内平行机身轴线并指向直升机前方为正；oy轴以垂直直升机参考面并指向直升机右方为正；oz轴以参考面内垂直xoy平面并指向直升机下方为正；θL，φL分别为直升机吊挂负载的侧摆角和后摆角。

图1 直升机吊挂系统示意图Fig.1 Schematic diagram of helicopter slung-load system

1.1 直升机动力学模型的建立

本文建立的六自由度无人直升机非线性系统模型处于悬停和低速平飞状态，首先假设[13]：(1)地面坐标系为惯性坐标系；(2)直升机是质量分布不变的刚体，质心不发生变化；(3)直升机严格左右对称；(4)忽略桨叶弹性形变，且主旋翼转速不变。

(1)

(2)

式中：

R11=cosθcosφ

R12=sinφsinθcosφ-cosφsinφ

R13=cosφsinθcosφ+sinφsinφ

R21=cosθsinφ

R22=sinφsinθsinφ+cosφcosφ

R23=cosφsinθsinφ-sinφcosφ

R31=-sinθ

R32=sinφcosθ

R33=cosφcosθ

(3)

H为姿态角到姿态角速度的转换矩阵，具体表达式如下[13]：

(4)

1.2 吊挂子系统模型的建立

本文建立的吊挂非线性动力学系统模型为刚体模型，为建立此模型，做以下假设[14]：

(1) 吊索为刚体，无重力和空气阻力；

(2) 吊索时刻处于紧绷的状态；

(3) 吊挂点处于直升机的重心的正下方；

(4) 吊挂负载处于较小角度振荡。

吊挂子系统的输出包括吊挂负载的后摆角φL和侧摆角θL，负载相对于吊挂点在图1所示坐标PL为[15]

(5)

式中：l为吊索的长度。吊挂负载相对于直升机重心的坐标P为[15]

P=PL+PH

(6)

式中：

(7)

其中：lH为吊挂点到直升机质心的直线距离；PH为吊挂点在以直升机重心为原点的机体坐标系的坐标。吊挂负载的绝对速度为[15]

(8)

负载作用在直升机上的力F与力矩Mb可表示为[15]

(9)

(10)

通过解算式(10)可得出吊挂负载的动力学方程，然后通过反步法解算出为达到减摆效果所需的直升机速度，最后控制直升机的速度即可达到减摆效果。

2 无人直升机吊挂系统减摆控制

无人直升机吊挂的减摆控制原理如图2所示[15]。

由图2可知，直升机刚体吊挂系统滑模减摆控制的原理如下：首先，通过反步法得到控制吊挂物摆角稳定的直升机速度；然后，设计滑模反步和反步控制器对直升机速度及姿态进行跟踪控制[16]，最终达到减摆效果。

2.1 吊挂摆角减振虚拟控制律解算

(11)

(12)

式中：

(13)

定义变量R，V为

(14)

摆角和摆角速度的跟踪误差可定义为

e1=Rd-R

e2=Vd-V

(15)

式中：Rd，Vd为摆角和摆角速度的期望输入。设计吊挂子系统反步法虚拟控制律为

(16)

结合式(14)～(16)，对e1求导可得：

(17)

设计减摆虚拟控制律为

(18)

式中：k1，k2为设计的正定矩阵。由于直升机吊挂负载处于较小角度振荡，可将矩阵A简化为以下形式：

(19)

根据吊挂子系统模型建立假设条件4将da简化，简化后的表达式为

(20)

根据假设条件4可得da不为0，且A为可逆矩阵。选择李雅普诺夫函数为

(21)

结合式(15)，(17)对式(21)求导可得：

(22)

2.2 直升机速度控制

直升机速度子系统采用反步法，系统共有三个输入Tmr，φ，θ，分别为主旋翼总矩输入、滚转角和俯仰角，三个输出u，v，w分别为直升机三个方向的线速度，并假设偏航角φ=0，直升机速度子系统可表示为

(23)

e3=Γ-Γd

(24)

(25)

(26)

设计速度子系统控制律为

(27)

式中：k3为设计的正定矩阵，可由直升机子系统模型解算出：

(28)

(29)

对式(29)求导得：

(30)

2.3 直升机姿态滑模反步控制

直升机姿态子系统采用滑模反步控制方法[18]。直升机姿态子系统的三个输入L，M，N分别为直升机所受三个方向的分力矩，三个输出φ，θ，φ分别为直升机的滚转角、俯仰角、偏航角。考虑姿态系统的未知干扰，则直升机姿态子系统可表示为

(31)

(32)

定义直升机姿态子系统的姿态角和姿态角速率的跟踪误差为

e4=Θd-Θ

e5=Ωd-Ω

(33)

(34)

式中：k4为设计的正定矩阵。对e4求导并将式(34)代入式(33)可得：

(35)

设计滑模面为

s=e4+e5

(36)

对式(36)求导，并将式(35)和式(33)代入可得：

(37)

最终设计姿态控制律为[19]

(38)

(39)

式中：γ>0为设计的参数。设计李雅普诺夫函数为

(40)

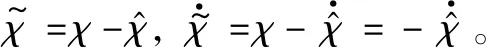
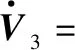
(41)

3 稳定性分析

以上关于直升机刚体吊挂耦合非线性系统减摆控制的稳定性分析可归纳为如下定理：

定理1：本文建立的刚性直升机吊挂非线性系统，对吊挂子系统(11)的减摆虚拟反步控制律按式(18)设计，对直升机速度子系统(23)的反步控制律按式(26)设计且对直升机姿态子系统(31)的滑模反步控制律和自适应律按式(38)～(39)设计，则闭环系统的所有信号收敛。

证明：选择李雅普诺夫函数为

(42)

将式(42)求导，并考虑式(15)，(17),(18)，(34)，(36)可得以下表达式：

(43)

式中：k5=min{2k1,2k2,2k3,2k4,2η-I}，由李雅普诺夫稳定性分析方法可知，本文所设计的无人直升机吊挂减摆系统是闭环稳定的，证毕。

4 仿真结果

为了验证直升机吊挂系统控制器设计的有效性，进行数字仿真，仿真参数如表1所示。

表1 仿真参数Table 1 Simulation parameters

通过Simulink仿真可得如图3～7所示的仿真结果。

图3 直升机吊挂减摆控制仿真结果Fig.3 Simulation results of helicopter anti-swing control

吊挂子系统与直升机速度子系统依然使用控制律(17)，(24)，设计直升机姿态子系统传统反步法虚拟控制律为

(44)

式中：k6为设计的正定矩阵，反步法控制律为

(45)

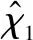
(46)

式中：γ1>0。

直升机姿态子系统反步法控制仿真参数如表2所示。Simulink仿真结果如图8所示。

表2 仿真参数Table 2 Simulation parameters

图8 系统传统反步控制仿真结果Fig.8 Simulation results of system traditional backstepping control

将系统参数m，Jxx，Jyy,Jzz摄动50 kg，20，15，25,参数摄动后的Simulink仿真结果如图9所示。

图9 参数摄动后系统滑模反步控制与传统反步控制仿真结果对比Fig.9 Comparison of simulation results between sliding mode backstepping control and traditional backstepping control after parameter perturbation

由图3可知，吊挂负载开始有一较小角度(本文假设初始摆角为0.1 rad)的摆动，通过所提出的一系列滑模反步和反步减摆跟踪控制，直升机吊挂负载得以减摆，由于直升机飞行速度较低，空气阻力相对于负载的重量较小，故吊挂负载几乎垂直于直升机前进，摆角稳定在0°左右。由图4和图5可知，直升机最终以初始速度(本文直升机x，y方向初始飞行速度均为5 m/s，z方向初始速度为0 m/s)于98 m的高度平飞，由图6和图7可知直升机姿态角速度和姿态角均稳定在0 rad/s和0 rad，最终对直升机速度与姿态以及吊挂子系统的摆角均完成跟踪控制，进一步证明了本文设计的一系列控制器的有效性。由图3以及图8～9可知，与传统的直升机吊挂系统的反步控制方法相比，本文设计的滑模反步控制方法具有对系统参数不敏感的特性，鲁棒性更强，且本文针对非线性系统进行跟踪减摆控制相对于线性横纵向解耦系统控制更具有现实意义。

图4 直升机速度仿真结果Fig.4 Simulation results of helicopter velocity

图5 直升机位移仿真结果Fig.5 Simulation results of helicopter displacement

图6 直升机姿态角速度仿真结果Fig.6 Simulation results of helicopter attitude angular velocity

图7 直升机姿态角仿真图Fig.7 Simulation results of helicopter attitude angle

5 结 论

本文针对建立的无人直升机刚体吊挂耦合非线性系统，以减小吊挂负载的摆角以及控制直升机速度和姿态为目标，对直升机速度和姿态，以及吊挂负载的摆角均进行了跟踪控制，并通过Simulink仿真对所设计控制器的有效性进行了验证。基于已有的理论基础，在不对直升机吊挂系统进行横纵向解耦和线性化的情况下，不仅对吊挂负载进行非线性减摆控制，也对直升机平面运动的速度以及姿态进行非线性控制，更具有现实意义，且滑模反步法对系统参数不敏感，闭环系统鲁棒性更强。但本文仅考虑直升机平面运动时的摆角控制，仅限小角度摆动，并且将吊挂负载视为质点，没有考虑其姿态建模，今后将对直升机空间运动的减摆控制展开研究。