旋流驻涡燃烧室预混燃烧流动特性数值分析

要晋龙，徐 青*，鄢平华，孙海俊

(1.华东交通大学 土木建筑学院，南昌 330013；2.江西应用科技学院 人工智能学院，南昌 330100；3.南昌航空大学 飞行器工程学院，南昌 330063)

0 引 言

高速来流下的火焰稳定是燃烧室设计过程重点关注的问题。20世纪90年代，Hsu[1]等人提出通过凹腔实现火焰稳定的驻涡燃烧室，相比于传统旋流燃烧室，驻涡燃烧室稳定工作范围宽、贫油熄火极限(LBO)以及污染物(NOx)排放进一步降低。在此基础上，双/三通道驻涡燃烧室[2-3]、液体燃料驻涡燃烧室[4-6]以及双凹腔驻涡燃烧室[1,7]等各类改进的驻涡燃烧室被相继提出。上述驻涡燃烧室研究大多是在低速来流(14～42 m/s)的航空发动机/燃气轮机工作状态下开展。此外，凹腔结构也越来越多地应用于超燃冲压燃烧室中[8]。

在冲压发动机燃烧领域，为探究驻涡燃烧室的可行性，文献[9-12]分别研究了冲压发动机流动工况下驻涡燃烧室的性能，实验结果表明：在高入口速度、压力及温度条件下，驻涡燃烧室依旧表现出优越的稳焰性能。文献[13]设计了一种带导流片的冲压发动机驻涡燃烧室，并对不同来流工况进行数值研究。文献[14]设计了一种燃烧室壁面高速旋转(30 000 r/m)的微型冲压发动机，并对其燃烧室性能进行了数值分析，研究表明：在燃烧室壁面高速旋转时的影响下，科氏力引起的凹腔旋涡破裂促进油气掺混，而在离心力作用下，主燃区形成的短回流区会造成燃烧室轴线附近燃料聚集，油气间掺混作用被削弱，火焰被拉长。文献[15]等将第二代旁侧凹腔驻涡燃烧室应用到微型冲压发动机燃烧室设计中，并对入口带旋流的燃烧室冷态流场进行了数值分析，结果表明：旋流条件下，凹腔内形成稳定的驻涡，在变工况时，凹腔驻涡保持稳定，且燃烧室流场的湍流强度提高。凹腔与旋流的组合稳焰方式为冲压发动机燃烧室性能提升提供了一个新的研究方向。

为进一步研究旋流流动对冲压发动机驻涡燃烧室性能的影响，本文基于文献[15]的研究，采用数值分析方法，深入分析不同旋流数对旋流驻涡燃烧室预混燃烧流动性能的影响，为旋流驻涡燃烧室的设计提供一定参考。

1 几何模型和计算条件

1.1 几何模型及工况

燃烧室结构尺寸如图1所示，其中燃烧室入口段(Inelt)直径D=50 mm，考虑到燃烧室中流动的充分发展，燃烧室长度取10D，凹腔结构参数：L/D=0.72，H/D=0.5。为便于研究，本文采用直接给出入口旋转速度的方式模拟旋流，旋流模拟工况如表1所示，其中旋流

表1 旋流计算工况Table 1 Swirl calculation working conditions

数的计算公式为

(1)

1.2 数值模型及边界条件

由于冲压发动机燃烧室入口流动Ma>0.3，所以在计算过程中考虑了气体的可压缩性，本文选用可压缩N-S方程求解。由于涉及到高旋流强度的计算，湍流模型选用线性压力应变(Linear Pressure-Strain)假设下的Reynolds Stress (7 eqn)模型[16]；选用甲烷为燃料，燃烧模型为单步反应的Eddy Dissipation Model(EDM)；近壁面采用标准壁面函数，控制方程离散格式为二阶迎风，对流通量离散采用Roe-FDS格式 。通过将流体运动类型设置为Moving reference frame，并输入旋转速度实现旋流模拟。燃烧室入口采用Pressure Far-Field边界条件，根据文献[14]，采用stream-thrust analysis推导得出：静压1.01 MPa，Ma=0.6，混气总温681 K，湍流强度20%，水力直径50 mm，燃料与空气在入口处已充分混合，总当量比为0.26。燃烧室出口为Pressure Outlet边界，出口压力为0.1 MPa，湍流强度20%，水力直径100 mm。壁面为绝热、无滑移壁面边界条件；同时为节约计算时间，采用1/4几何模型进行计算，并设置为周期性边界条件。

1.3 网格独立性及燃烧模型验证

1/4模型采用六面体结构化网格进行划分，如图2所示。网格独立性检验结果如图3所示，21万网格与41万网格的计算结果差异较小，可认为21万网格已达到网格无关性要求，各工况均采用21万网格数进行数值计算。

图2 燃烧室1/4模型网格划分Fig.2 Grid division of combustor 1/4 model

图3 燃烧室中心线上的温度分布Fig.3 Temperature distribution at the center line of combustor

关于湍流模型的验证可参见文献[17]，燃烧模型验证如图4所示，选用文献[1]中的燃烧室模型，模拟在入口空气速度Uair=42 m/s、燃烧室总当量比Φo=0.21、凹腔局部当量比ΦP=4.4工况时，凹腔中部z=24 mm处的温度分布，并与实验结果进行对比，由于文献中没有给出具体温度测点位置，所以选取了三个不同角度(0°，11.25°，22.5°)截面的温度分布。从图4可以看出，在0°截面的计算值与实验值的相对误差小于0.08，认为两者吻合较好，从而验证了本文所选数值计算模型的合理性。

图4 模型验证Fig.4 Model validation

2 计算结果分析与讨论

2.1 流场特性

图5为不同旋流数时燃烧流场中z=0平面的凹腔内速度流线图。由图可见，凹腔处于低速区，在涡心位置处流速约在20～40 m/s，远小于主流速度，这为实现凹腔内的点火以及火焰稳定提供了速度条件。对比流线分布，在各个旋流工况下凹腔内均形成单涡结构，而且这些旋涡的滞止点都位于凹腔后体壁面，所以，凹腔内的流动处于被挤压阶段[18]。在不同旋流强度下，凹腔内旋涡的涡心位置有所差别，当旋流数S=0时，旋涡的涡心位于凹腔左上角，因此旋涡的上部和左侧发展受到凹腔壁面的阻碍，而旋涡右侧和下侧发展更为充分，引起旋涡被挤压的原因可以根据燃烧引起的“热缩”效应[19]来解释；当旋流数S>0时，凹腔内旋涡的涡心高度回到凹腔的中间位置，根据稳定旋流中径向力平衡公式[14]

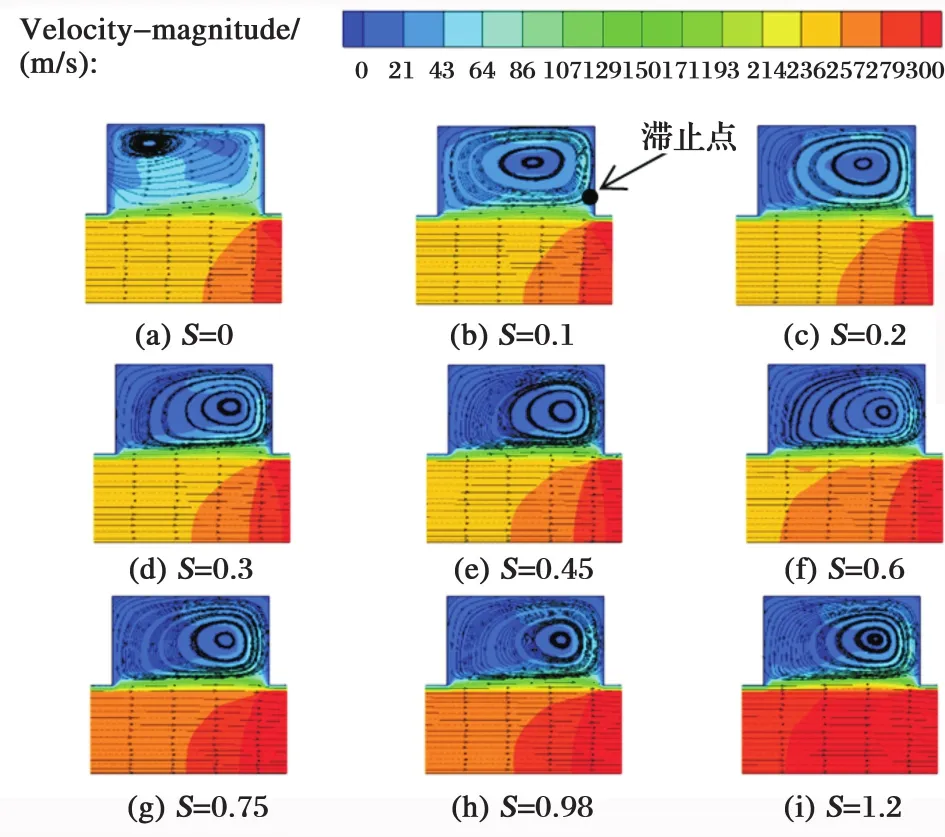
图5 凹腔局部速度流线图Fig.5 Partial velocity streamlines of cavity

(2)

式中：Ω表示角速度；Ω2r表示离心力；ρ为流体密度，p为流场静压。由于离心力方向为径向，所以离心力通过径向压力梯度来平衡。当S>0时燃烧室中引入旋流，凹腔内流体的旋转产生了离心力，从而产生了径向压力梯度，因此，涡心在径向压力梯度的作用下，重新回到凹腔中间高度水平。另外，当S=0.1时，旋涡的涡心基本位于凹腔的几何中心，而随着旋流数继续增大，涡心会稍微向右移动。

工程上，通常采用湍动能来表示流动过程中湍流的强弱。图6描述了旋流数S=0和S=0.1时，燃烧室中Z=0截面的湍动能分布。从图中可以看出，在两种旋流工况下，湍动能分布基本相同，凹腔内由于流速低，因此湍动能较小，减少了流动过程中的脉动，利于凹腔内火焰的稳定；而高湍流强度区域，主要集中在凹腔后的台阶面附近，并向后延伸，主要是由于在台阶面附近的突扩区域主流与回流区之间的强烈掺混作用引起的，并由此而促进该区域中未燃气体与高温烟气之间的热量传递，激发了燃烧反应，结合燃烧室总体温度分布可以看出，在该区域内进行了明显的燃烧过程。

图6 燃烧室三维流线图及Z=0平面湍动能分布Fig.6 Combustor 3D streamlines and turbulent-kinetic energy distribution at plane Z=0

然而根据两种工况下的三维流线图，在凹腔内均形成了旋涡，而在凹腔之后的突扩区域，对于S=0工况，只在台阶面附近形成回流区，这个回流区的形成主要是由于突扩区域产生的总压损失引起流动分离而产生的压力梯度涡[14]，容易受到流动工况的影响；对于S=0.1工况，在台阶面之后出现了流体的三维旋转，而在二维流线图中同样表现为一个回流旋涡，其成因如下：由于在燃烧室入口引入旋流，虽然流体在凹腔下游进入了面积更大的突扩区域，但是对于那些进入更小直径区域的流体而言，为保证动量守恒，必须以更大的角速度旋转，此时，根据公式(2)可以看出，角速度Ω增加，离心力Ω2r也随之增加，所以就需要产生更大的径向压力梯度∂p/∂r来平衡离心力。也就是说，在台阶面附近产生低压区，引起流体的反向旋转，从而形成旋涡回流区[14]，又因为在燃烧室后段，旋流的影响逐渐消失，所以流体重新回到最初的旋向，而旋转强度逐渐减弱。

根据以上分析，虽然在S=0.1时，燃烧室内形成了三维旋转流场，但是流场的湍动能并没有因此而显著提高，说明弱旋流对于流场湍流水平的影响不大，这样就可以避免过强的湍流流动引起耗散而增加总压损失的问题，三维的旋转流动对于燃料与氧化剂以及燃料与高温烟气的掺混却大有裨益，由于本文计算采用预混气体，所以三维旋转对于掺混过程的影响并不明显。

2.2 总压恢复系数

总压恢复系数是评价燃烧室流动过程中不可逆损失大小的一个重要参数，计算公式为

(3)

图7为燃烧室总压恢复系数与旋流数之间的关系。可见，随着旋流数的增加，总压恢复系数σ*先增加后降低再增加。当S=0.1时，σ*达到最大值0.851，而S=0.98时，σ*最小，这表明，旋流强度过大会使流体的流动损失增加量大于燃烧过程中流体内能和动能的增加量，导致总压恢复系数降低。而在S=1.2时，由于旋流强度很高，在流动过程中引入了很大的切向速度，使得燃烧室内动能大幅增加，但考虑到高速流动带来的流动损失，此时总压恢复系数虽有所上升，但依旧处于较低的水平。

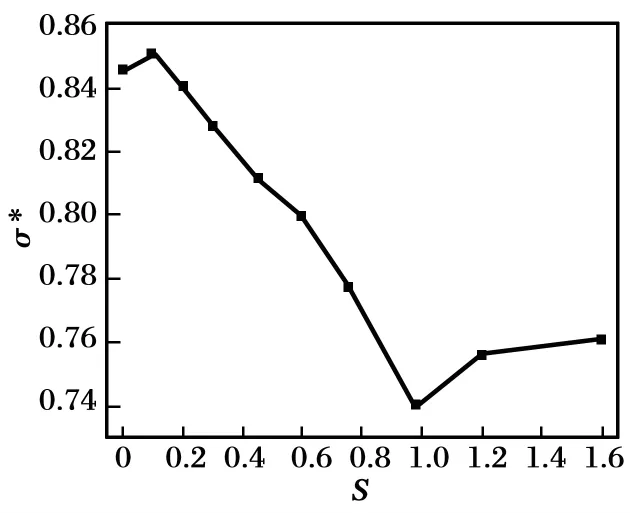
图7 不同旋流数下燃烧室总压恢复系数Fig.7 Combustor total pressure recovery coefficient at different swirl number

2.3 燃烧室温度分布

燃烧室总体温度分布如图8所示。从图中可以看出，燃烧室的高温区域基本分布在凹腔内以及凹腔后的台阶面附近，主要是由于在这两个区域中形成了旋涡回流区，一方面，回流区低的流速可以保护火焰不被高速主流吹熄；另一方面，回流区的卷吸作用能够促进未燃气体与高温烟气之间的热量传递，为维持燃烧反应提供温度条件。此外，当S=0时，台阶面高温区靠近燃烧室壁面，容易造成局部壁面超温的现象；而当S=0.1时，该高温区域逐渐远离壁面并向燃烧室中心轴线附近扩展，这主要由于在径向压力梯度的作用下，回流区向远离壁面的方向移动，这样一来能够有效缓解旁侧凹腔带来的火焰壁面局部温度过高的现象[20]；当旋流数继续增加时，台阶面后的高温区域分布变得更加复杂，且火焰长度明显大于S=0和S=0.1时的火焰长度，当S>0.3时，高温区又重新回到了燃烧室壁面附近，这是由于燃烧室引起的“热缩”效应[19]，对台阶面后回流区的挤压强度超过了旋流引起的径向压力梯度而使回流区重新回到近壁面的位置，同时根据图9中S=0.3时的压力及流线图可以看出，此时的台阶面后的回流区一直延伸到燃烧室出口，而旋流的影响则主要集中在燃烧室入口附近区域，所以在燃烧室出口附近区域压力变为轴向分布，径向压力梯度基本消失，使得后半段火焰难以向燃烧室中心扩展，而又重新回到近壁面处；在S=0.6和S=1.2时，由于回流区长度较长，在沿燃烧室长度方向上回流区与主流交界面处由于强烈的动量及热量交换，也会发生小范围的燃烧，这种局部间断的燃烧现象，会造成燃烧室内压力波动过大，对燃烧的稳定工作会产生不利影响；另外，在S=1.2时，凹腔以及台阶面处的高温区域温度及面积明显小于其他工况，表明在凹腔以及台阶面附近的燃烧效率较低，而在燃烧室出口却出现了大面积的高温区，这对燃烧室以及喷管工作的稳定性和可靠性产生负面影响。根据以上分析可以看出，当旋流数S=0.1时，台阶面火焰向燃烧室中心扩展，且火焰长度短，燃烧集中。

图8 燃烧室温度分布云图Fig.8 Combustor temperature contours

图9 S=0.3时的燃烧室压力分布和流线图Fig.9 Combustor pressure distribution and streamlines at S=0.3

2.4 燃烧效率

燃烧效率表示燃烧室内燃料燃烧的完全程度，本文采用焓增法来计算燃烧效率，公式为

ηc=

(4)

不同旋流数时的燃烧效率如图10所示。从图中可以看出，在不同的旋流工况下燃烧室的燃烧效率ηc>0.93。当旋流数S≤0.1时，燃烧效率ηc>0.96，结合图8的温度分布可知，在S=0和S=0.1时，燃烧室在短距离内高效完成了燃烧过程；随着旋流数增大(0.2≤S≤0.98)，燃烧效率均低于0.96，虽然在温度图中这些旋流工况下燃烧室的高温区域面积很大，但是燃料的燃烧效率却不高；另外，当旋流数S=1.2时，由于在燃烧室出口出现二次燃烧现象，导致燃烧效率出现骤升。

图10 不同旋流数时燃烧效率Fig.10 Combustion efficiency at different swirl number

图11所示为三种旋流工况下燃烧效率沿燃烧室长度方向的变化关系。在不同旋流工况下，燃烧效率沿燃烧室长度方向的变化规律基本相同：在燃烧室入口段由于流速高、温度低，未发生燃烧反应，从凹腔前体开始燃料与氧化剂反应，燃料的燃烧效率逐渐上升，直至该工况下最高的燃烧效率。但是，在x/D≤2时，三种旋流工况下燃烧效率沿轴线方向变化基本一致；当x/D>2，旋流数S=0和S=0.1时，燃烧效率沿轴向速度明显快于S=1.2工况，且S=0和S=0.1时，分别在x/D=6.4和x/D=6.6达到最高的燃烧效率ηc=0.966，而S=1.2时，在x/D=8时才达到最高的燃烧效率ηc=0.982，这说明S=0和S=0.1工况能够在更短的距离内实现更高效的燃烧，这样就有望将燃烧室的长度缩短到x/D=7左右，从而能够进一步提高发动机的推重比。

图11 燃烧效率沿燃烧室长度方向的变化Fig.11 Variation of combustion efficiency along the x/D

综合流场特性、燃烧室总压恢复系数、温度分布和燃烧效率等因素，认为旋流数S=0.1时，燃烧室的性能更为优异。

3 结 论

本文以冲压发动机旋流驻涡燃烧室为研究对象，采用数值计算方法，分析了旋流强度对预混燃烧条件下燃烧室的燃烧流动特性的影响规律，获得如下结论：

(1) 对比有、无旋流时流场特性：在凹腔内均形成光滑的单涡结构，当旋流数S=0.1时，涡心最接近凹腔的几何中心，且在弱旋流工况下(S=0.1)，三维旋流的引入并没有过大增加燃烧室流动的湍动能，避免了过大的湍流强度带来的流动损失；

(3) 当旋流数S=0.1时，燃烧室火焰长度缩短，火焰向燃烧室中心扩展，燃烧室的燃烧效率较高，且有望缩短燃烧室长度。

因此，燃烧室在弱旋流工况下有更好的燃烧流动特性，同时也符合发展高推重比发动机的趋势。然而，本文中只研究了单一当量比预混燃烧特性，在实际的驻涡燃烧室中更多采用扩散燃烧方式，所以应进一步开展燃烧室变当量比以及非预混燃烧时性能表现的相关研究。