高原环境下小型旋翼悬停性能数值模拟研究

姜心淮，赵良玉，李兴城

(北京理工大学 宇航学院，北京 100081)

0 引 言

我国领土面积广阔，地貌复杂多样，高原地区约占总领土面积的26%，主要覆盖我国重点防御的边疆地区，其环境恶劣、自然灾害频发。小型旋翼无人机具有垂直起降、原地回转、自由悬停等独特优势[1-2]，可应用于高原地区弹载蜂群、边防巡查、包裹投递、抢险救灾等，在民用和军用领域都具有重要意义。

多年的研究积累和飞行试验表明，在平原执行飞行任务的旋翼飞行器很难在高原环境中保持同等级别的工作性能。复杂的高原环境对旋翼飞行器性能的影响有多个方面，仅就气动性能而言，旋翼提供飞行所需的绝大部分动力，是旋翼飞行器稳定飞行的主要依靠[3]。文献[4]指出高原环境下直升机的旋翼性能明显下降，主要是由于高原环境气压、空气密度低等物理因素造成的。高原环境会对旋翼气动性能带来更大的不利因素，导致执行高原任务的旋翼飞行器航行时间短、有效载荷低、可靠性和安全性差等，严重时甚至无法成功起飞[5-6]。因此，有必要对高原任务环境下旋翼的气动性能进行研究分析。

国外对高原环境旋翼性能的研究成果并不多，国内学者更关注高原环境对直升机性能的影响规律。田磊等[7]研究了直升机高原悬停时的地面效应，针对高原地面效应函数模型的不足，提出了一种适合高原环境的修正函数。黄启斌[8]分析了无人直升机在高原环境下的起降能力，针对高原环境发动机起飞功率下降快的问题，提出了使用高性能发动机和大直径旋翼的结论。徐自芳等[9]对直升机高原飞行性能计算方法进行了研究，基于叶素理论和飞行动力学模型提出了一种适合高原地区的高精度直升机飞行性能计算方法。蔡伟等[4]采用自由涡理论模拟桨叶空气动力的作用，分别对UH-60“黑鹰”直升机在低海拔及高海拔地域的旋翼性能开展悬停状态的计算和分析，得出高原环境下直升机旋翼性能显著下降、需要发动机具有足够功率储备的结论。

上述对旋翼飞行器的研究多为全尺寸旋翼的直升机，对小型旋翼飞行器在高原环境下的气动性能则鲜有研究。小型旋翼无人机因尺寸小、速度慢的特点，一般在雷诺数低于105范围内飞行，远低于常规全尺寸飞行器，高原环境使其雷诺数水平进一步降低[10]。低雷诺数使粘性力的影响水平更接近惯性力，基于高雷诺数假设的直升机旋翼理论并不能对小型旋翼气动性能给出可靠的预测[11]。因此，准确预测并研究小型旋翼高原环境下的气动性能是一项具有挑战性的工作。

本文根据计算模型特点，采用适用于求解小型旋翼悬停流场的数值模拟方法，计算了不同转速条件下旋翼的气动性能，并通过拉力试验验证了该方法的准确性，继而采用该数值模拟方法分别预测了T-Motor P15×5旋翼转速相同海拔不同的悬停性能及海平面和5 km高原环境不同转速的悬停性能。

1 数值模拟方法

采用T-Motor P15×5作为研究对象，其旋翼直径为381 mm。通过三维扫描技术获得其坐标点，并应用三维建模软件建立其几何模型。为了能够准确预测小型旋翼高原任务环境下的悬停性能，对旋翼周围流场区域进行高质量网格划分，采用CFD方法对不同转速条件的旋翼进行数值模拟，最后通过旋翼拉力试验测得的数据验证数值模拟方法的准确性。

1.1 网格划分及数值模拟

采用软件ANSYS ICEM 18.2对T-Motor P15×5旋翼进行结构网格的划分。结构网格具有数据结构简单、网格质量好、收敛速度快等优势[12]。将旋翼结构网格分为两部分：一部分是包裹桨叶的圆柱体旋转区域，该区域底面直径为1.1倍旋翼直径，高为0.2倍旋翼直径；最大网格尺寸小于8 mm，旋翼表面第一层网格厚度取足够小，以保证y+≤1；网格整体尺度以旋翼为中心向外线性增长，增长率小于或等于1.1，网格节点数约为261.7万。旋转域网格如图1所示。

图1 旋转域网格Fig.1 Mesh in the moving reference frame

另一部分为包围旋转域的固定区域网格，采用圆柱体形状，上下底面和圆柱面与旋翼几何中心的距离均为25倍旋翼半径[13]；网格最小尺寸约为3 mm，以旋转域为中心向外线性增长，增长率为1.1，网格节点数约为37.5万。固定域网格如图2所示。

图2 固定域网格Fig.2 Mesh in the stationary reference frame

数值模拟采用ANSYS FLUENT 18.2，其遵循微分形式的三维雷诺平均Navier-Stokes方程：

(1)

式中：ρ为密度；t为时间；ui和uj分别为xi方向和xj方向的Favre平均速度(i，j=1，2，3)；P为静压；μ为动力粘度；e为单位体积的能量；q为由热传导产生的热流。

采用结合了ω方程和ε方程的SSTk-ω湍流模型，近壁面区域和远离壁面区域分别采用k-ω湍流模型和k-ε湍流模型，兼顾了鲁棒性和对自由流的敏感性，且在预测低雷诺数壁面边界层特征方面较S-A湍流模型具有更高的精度，适用于小型旋翼悬停流场的求解[14]。

数值模拟采用基于密度的双精度稳态求解器，空气视为理想气体，粘性系数由Sutherland公式给出。采用多参考坐标系(MRF)方法，将旋转域和固定域通过交界面分割开来，包裹桨叶的旋转域相对固定域做匀角速度旋转运动。该方法的原理是将惯性系中的非定常问题转化为运动坐标系的定常问题，是一种稳态近似。圆柱体远场边界的上下底面分别设置压力入口、压力出口边界条件，圆柱面设置为无滑移壁面。梯度的空间离散采用基于网格单元的最小二乘法，对流项、湍流动能和比耗散率的空间离散均采用二阶迎风格式。

1.2 旋翼拉力试验

为验证本文数值模拟方法的准确性，采用旋翼拉力测试系统进行该旋翼的拉力试验。整个测试系统分为驱动系统、测量系统、底座和辅助系统四部分，如图3所示。压力传感器采用轮辐式拉压力称重传感器DYLY-102(0～20 kg)，转速传感器为欧姆龙光纤放大器E3x-a21，传感器供电为DC12V 60 mA。试验过程通过遥控器控制输入电流，从而起到控制旋翼转速的作用，通过转速显示仪表确定当前转速，分别测量了3 000 r/m,3 300 r/m,3 600 r/m,3 900 r/m,4 200 r/m,和4 500 r/m六种转速情况下的拉力数据。

图3 小型旋翼拉力测试系统Fig.3 Tension test system of the small rotor

1.3 数值模拟方法验证

利用数值模拟方法，对单个T-Motor P15×5旋翼进行了悬停状态的数值模拟，计算了与拉力试验相同的六个状态，将数值模拟结果同试验数据进行对比，如图4所示。可以看出，数值模拟和试验测得的结果符合较好。在3 000 r/m到4 200 r/m转速范围内，试验测得的拉力略小于数值模拟数据，而在大于4 200 r/m的转速下，则情况相反。3 000 r/m至4 200 r/m转速范围内，误差随着转速的增加先增大后减小，3 000 r/m转速条件下拉力误差约为1.6%，3 300 r/m的误差达到最大，约为4%，而当转速提高到4 200 r/m时，误差仅为0.14%。

图4 不同转速的旋翼拉力数据对比Fig.4 Tension comparison of the rotor at different rotating rates

总之，无论是从变化趋势，还是计算精度上来看，本文所采用的小型旋翼在其常规转速条件下的数值模拟结果都能较好地符合试验数据，说明本文所采用的数值模拟方法能较准确地预测小型旋翼在低雷诺数条件下的气动性能。

2 高原环境小型旋翼悬停性能分析

为研究小型旋翼高原环境下的气动性能，采用同样的数值模拟方法，对不同状态的小型旋翼悬停性能进行了预测。

2.1 不同海拔高度旋翼气动性能分析

标准大气压下，海平面大气温度为T0=288.15 K，压强为p0=101.325 kPa；对流层中，海拔高度每增加1 km，温度减小6.5 ℃[15]。高度h处的气温为

T=288.15-0.006 5h

对流层中忽略重力加速度随高度的变化，将其视为常数，则高度h处的大气压强ph只和该处的温度有关，其计算公式为

(2)

为研究小型旋翼悬停性能受海拔高度的影响，本文计算了海平面到5 km海拔高度的大气温度和压强，海拔每增加1 km计算一组数值。根据计算得到的大气参数进行T-Motor P15×5旋翼在不同海拔高度条件下的气动性能预测，计算状态为悬停，旋翼转速为4 500 r/m。图5～6分别为数值模拟得到的不同海拔高度下旋翼的拉力和功率值。

图5 不同海拔高度旋翼拉力Fig.5 Tension of the rotor at different altitudes

从图中可以看出，在海平面到海拔5 km范围内，随着飞行高度的增加，小型旋翼的拉力和功率有明显下降，下降趋势没有明显变化，飞行高度较低时变化率较大，较大飞行高度的变化率略有下降，整体下降趋势近似线性。与海平面处相比，海拔5 km处的旋翼拉力降低约41.2%，功率降低约40.4%。

图6 不同海拔高度旋翼功率Fig.6 Power of the rotor at different altitudes

图7分别为海平面大气条件下旋翼下表面、上表面的压力云图和海拔5 km大气条件下旋翼下表面、上表面的压力云图。由桨根到桨叶中段，旋翼上下表面压力变化相对平缓，下表面压力略大于上表面。桨叶中段向桨尖过渡区域，旋翼上表面压力有明显下降，下表面压力明显上升；靠近桨尖处上表面压力由桨叶后缘向桨叶前缘呈逐渐减小趋势，在桨叶前缘处压力达到最小；下表面压力由桨叶前缘、后缘向中间逐渐增大， 靠近中心的位置压力达到最大。由桨根到桨叶中段，旋翼上下表面的压力差较小，而桨叶中段到桨尖区域上下表面的压力差较大，为旋翼提供飞行所需的升力。

图7 旋翼表面压力云图Fig.7 Contour of pressure of the rotor surface

在海平面和海拔5 km两种不同的大气条件下，旋翼上下表面的压力云图在形态上并没有明显的不同，最大的区别是数值上的变化。图8为将压力范围扩大到包含两个计算状态的压力值得到的压力云图，更直观地描绘出两种状态旋翼表面压力在数值上的差异。在海平面大气条件下，旋翼表面压力分布最低约为93 728.7 Pa，最高约为105 475 Pa；海拔5 km条件下，旋翼表面压力分布最低约为49 664.8 Pa，最高约为56 518.5 Pa。

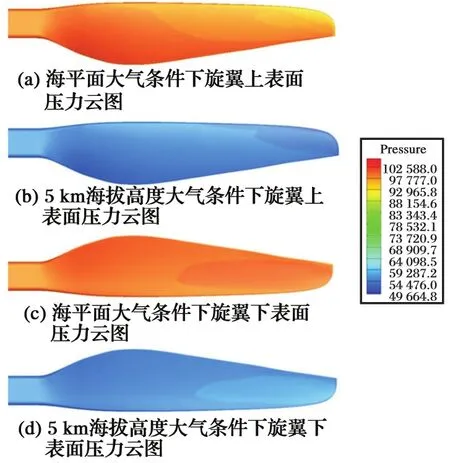
图8 不同海拔旋翼表面压力云图对比Fig.8 Pressure contour of the rotor surface at different altitudes

因此，就压力分布而言，可认为由于海拔高度不同导致的温度、大气压强和空气密度等大气条件的变化对小型旋翼悬停状态的表面压力分布规律无显著影响，气动外形相同的旋翼，在不同海拔高度条件下表面压力分布规律基本相同。而对于在不同海拔高度，旋翼表面承受压力的大小而言，相同转速条件下，海拔5 km与海平面相比旋翼表面低压减小约47%，高压减小约46.4%。所以，对于不同海拔高度使用的小型旋翼来说，如果要在同样的旋翼半径和同样的转速条件下维持相等或相近的拉力性能，有必要对其几何构型展开优化设计。

2.2 不同转速旋翼气动性能分析

为研究不同转速对旋翼悬停性能的影响，分别计算了在海平面和5 km海拔两种条件下不同转速旋翼的气动性能。同样选取上述的六个转速，在两种大气环境下不同转速的拉力和功率对比如图9～10所示。

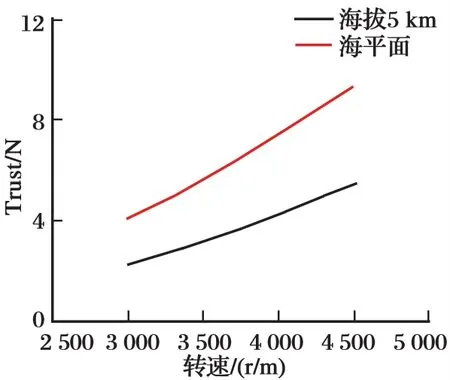
图9 不同转速旋翼拉力Fig.9 Tension of the rotor at different rotating rates

随着转速的增大，旋翼拉力和功率随之增大。拉力增大趋势近似线性，与海平面相比，5 km海拔高度旋翼拉力增长趋势较平缓。海平面大气环境下，从3 000 r/m到4 500 r/m，拉力增加了近130%，约为5.3 N；在5 km高原大气环境下，从3 000 r/m到4 500 r/m，拉力增加了近141.2%，约为3.23 N。转速越大，功率增长越快，与海平面相比，5 km海拔高度旋翼功率增长相对缓慢。海平面大气环境下，从3 000 r/m到4 500 r/m，功率增加了近243%,约为68 W；海拔5 km大气环境下，从3 000 r/m到4 500 r/m，功率增加了近242.8%，约为40.5 W。

图10 不同转速旋翼功率Fig.10 Power of the rotor at different rotating rates

3 结 论

本文利用CFD技术研究了高原大气环境下小型旋翼的悬停性能，从不同海拔高度、不同转速多种角度进行分析，通过拉力试验技术验证了CFD方法的准确性。

(1) 旋翼悬停状态的数值模拟结果能够较好地与试验数据吻合，本文采用的数值模拟方法可以较为准确地预测与本文运动状态相似、尺度相似的旋翼悬停性能。

(2) 与海平面处相比，在海拔5 km条件下，旋翼拉力和功率均有明显下降，即小型旋翼在高原环境下的拉力和功率均有显著下降。

(3) 高原大气环境对旋翼表面的压力分布规律无显著影响，旋翼表面压力数值具有显著差异，这是造成旋翼拉力在高原环境下明显下降的根本原因。

(4) 需要在同样旋翼半径和同样的转速条件下，维持相等或相近的旋翼拉力，建议对高原环境下的旋翼几何形状进行优化设计。