基于邻域最优控制律的再入轨迹在线修正

李世杰，李 炯，刘 滔，陈文钰

(1.空军工程大学 防空反导学院，西安 710051；2.中国空气动力研究与发展中心 计算空气动力研究所，四川 绵阳 621000；3.中国空气动力研究与发展中心 空气动力学国家重点实验室，四川 绵阳 621000)

0 引 言

高超声速飞行器再入大气层，初始能量巨大，飞行速度较高，过程非常复杂，必须寻找一种快速可行轨迹优化的方法。再入轨迹优化问题实质上是一个带有状态约束和控制约束条件的非线性最优控制问题，当前求解最优控制问题的方法主要有间接法和直接法两类[1-4]。其中，间接法利用Pontryagin极小值原理和一阶最优必要条件，将最优问题转换为两点或多点边值问题。这种方法控制参数较少，方程积分性好，不易发散，但对初值敏感。

间接法满足最优性一阶必要条件，且其解的精度较高。邻域优化算法就是在其基础上发展起来的[5-6]，该方法相比于一阶变分的最优控制方法，具有二阶精确度，且最为重要的特点是，在一阶最优弹道小邻域范围内，能够一次计算满足一族初始或终端约束的最优弹道族，非常适用于形成优化弹道数据。

相比间接法，直接法对初值不敏感，其利用参数化方法将连续空间的最优控制问题转化为NLP问题，然后再利用NLP问题求解工具[7]进行求解。直接法在解决实际复杂问题上具有优势[8-9]，其典型代表就是伪谱法。近年来，由于伪谱法的快速求解效率，已逐渐成为求解轨迹优化问题方法的研究热点[10-15]。

文献[12]基于Radau多段伪谱法对最优机动突防弹道进行了求解，将突防脱靶量提高到百米量级，充分发挥了高超声速飞行器的纵向机动性能，同时也证明了伪谱法处理弹道优化问题的优越性。文献[13]基于伪谱法研究了高超声速助推-滑翔飞行器的最大化射程以及最大化横程的弹道优化问题。文献[14]研究了基于间接Legendre伪谱法的最优制导律，通过Legendre伪谱法离线获得参考轨迹，通过LQR方法在LG配点上求得控制量的修正值。文献[15]在文献[14]的基础上，研究基于间接Radau伪谱法的轨迹跟踪控制律，两者的不同之处在于配点的选择不同。文献[14-15]中制导律的计算不需迭代及求解Riccati方程等复杂数值计算，能快速获得控制量的修正值，但未解决增益矩阵的选择问题，对计算结果影响较大。本文在此基础上，提出基于邻域最优控制的再入轨迹制导律，首先基于分段Radau伪谱法获得最优参考轨迹，基于参考轨迹将最优控制问题转化为状态量偏差与协态量偏差的两点边值问题，然后求解LGR(Legendre-Gauss-Radau)配点上的最优反馈控制律，解决了LQR法的增益矩阵选择问题，对初始状态量的较大范围偏差具有良好的鲁棒性，并且能够满足实时性的需求。

1 再入轨迹制导问题

1.1 再入滑翔运动模型

忽略地球自转的影响，高超声速飞行器再入飞行的三自由度运动模型建立如下：

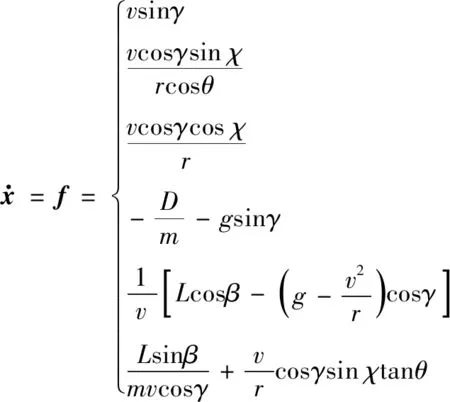
(1)

式中：飞行器的状态量x=(r,φ,θ,v,γ,χ)，分别为地心矢径、经度、纬度、速度、航迹倾角、航迹偏角；控制量u=[α,β]，分别为攻角和倾侧角；m为飞行器质量；g=μ/r2为重力加速度，μ=398 603.2 km3/s2为地球引力常数)。

升力L和阻力D分别为

(2)

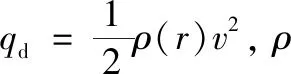
CL(α)=CL0+CLαα

CD(α)=CD0+CDαα+CDα2α2

(3)

式中：CL0=-0.207 0；CLα=1.676；CD0=0.078 54；CDα=-0.352 9；CDα2=2.040；α为攻角。

1.2 再入约束条件

再入约束包括过程约束、终端约束及控制量约束，其中过程约束主要有动压约束、过载约束、状态量约束及热流密度约束等。

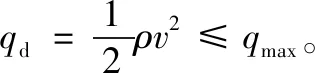
热流密度约束：Q=QaQr≤Qmax。

式中：Qa=h0+h1α+h2α2+h3α3，h0=1.067，h1=-1.101，h2=0.698 8，h3=-0.190 3；Qr=CρNvM，N=0.5，M=3.07，C=9.289×10-9(kJ/m3.57)/kg。

其他变量约束-89°≤χ≤89°,-89°≤γ≤89°。

初始条件：r0=(Re+79.248) km,θ0=0°,φ0=0°,v0=6.492 km/s,γ0=-1.5°,χ0=0°。

终端约束条件包括位置、速度和角度等，即rf=(Re+24.384) km，vf=0.762 km/s，γf=-10°。其中：Re是平均地球半径。

优化轨迹以最大化经度为目标函数，同时满足上述一系列约束条件：

J=min{-θf}

(4)

1.3 最优参考轨迹的生成

最优轨迹生成即求解控制量u=[α,β]，使目标函数最小(或最大)，并且状态满足运动方程及各种约束条件。轨迹优化问题可当成是一般的最优控制问题。首先需将最优控制问题的时域[t0,tf]转化为[-1,1]区间，对时间变量做变换，即

(5)

为不失一般性，考虑Bolza形式的一般最优控制问题，性能泛函指标为

(6)

式中：状态变量x(t)∈Rn；初始时间和终端时间t0,tf(自由或固定)满足动力学微分方程约束。

(7)

初始状态x(t0)=x0，终端边界条件约束为

N[x(tf),tf]=0

(8)

针对上述典型的两点边值最优控制问题，采用文献[16]中的分段Radau伪谱法进行求解。该方法在求解中采用Legendre多项式进行状态量、控制量和协态量估计与离散化，将微分约束转化为代数约束，将最优控制问题转化为非线性规划问题，再采用非线性规划求解器SNOPT[7]等进行求解。针对上述飞行器再入过程，采用文献[16]中的分段Radau伪谱法计算最优参考轨迹。

2 再入轨迹在线修正问题

2.1 邻域最优控制问题

由于随机扰动及系统误差，飞行器的实际飞行轨迹与最优参考轨迹并不一致。为解决此问题，一般是重新规划最优轨迹，但这种方法计算量较大，花费时间较多，难以实现；另一种方法是采用邻域最优控制理论，通过计算获得控制量的修正值。邻域最优控制问题描述如下：

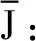
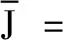
(9)

设u*(t)为最优控制，x*(t)为由此产生的最优曲线，存在与之相对应的协态λ*(t)，根据极小值原理，满足正则方程：

(10)

哈密尔顿函数为

H(x,u,λ,t)=L(x,u,t)+λTf(x,u,t)

(11)

最优控制条件为

(12)

若终端状态受约束，则边界约束条件为

(13)

若终端状态自由时，则边界约束条件为

(14)

不论终端状态，终端边界条件可统一为

ψ[x(tf),λ(tf)]=0

(15)

若终端时刻自由时，确定tf的终端横截条件为

(16)

考虑飞行器实际飞行轨迹与最优参考轨迹的细小初始偏差δx(t0)，初始偏差会产生状态量、协态量及控制量与最优参考轨迹的偏差，分别为δx，δλ和δu，对其进行局部线性化得

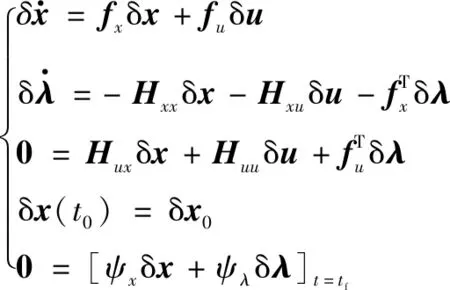
(17)

当Huu为非奇异矩阵时，可得

(18)

式(17)中，δx(t)和δλ(t)的状态方程及初始条件δx(t0)=δx0与终端约束条件0=[ψxδx+ψλδλ]t=tf形成了δx(t)和δλ(t)的线性两点边值问题。

2.2 邻域最优控制律设计

最优参考轨迹是在域[-1,1]中求解的，所以邻域最优控制设计在此域中，状态和协态偏差量微分及边界条件转换为

(19)

δx(τ0)=δx0

(20)

ψxδx(τf)+ψλδλ(τf)=0

(21)

伪谱法是将状态变量与控制变量在LGR点上进行离散[16]，在区间Sk,(k=1，2，…，K)中，利用Lagrange 插值方法对状态量偏差量δx(τ)和协态变量偏差δλ(τ)在LGR点进行近似：

(22)

(23)

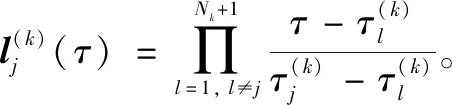
利用LGR点处近似值的微分仍为代数形式，对状态量偏差量和协态变量偏差微分得

(24)

(25)

(26)

(1+τi)[PNk(τi)-PNk-1(τi)]，PNk(τi)为Nk阶Legendre多项式。从而有

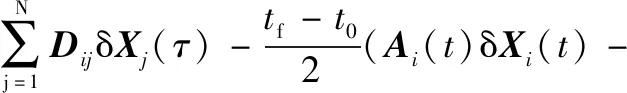
(27)

式中：i=1，2，…，N

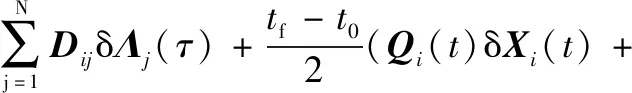
(28)

式中:

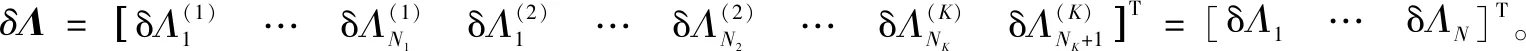
为计算简便，令

(29)

(30)

(31)

(32)

式中:In与0n分别为n×n阶单位矩阵和n×n阶零矩阵，则有

(33)

(34)

边界条件为

δx(t0)=δx0

(35)

ψxδxN+ψλδλN=0

(36)

为解方程式(33～34)，将其与边界条件合并，则有

(37)

式中:P1与P2为n×n的N阶矩阵，P1=[0n,…,0n,ψx]，P2=[0n,…,0n,ψλ]。令ZT=[XT,ΛT]，V=[V1,…,Ve]，可得

V1δX1+VeZe=0

(38)

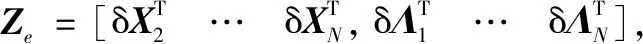
Ze=-VeV1δX1=WδX1

(39)

式中：为MATLAB中的左除算子。令Z=[δX1Ze]T，则可得

(40)

式中：Wx和Wλ为[InW]T的分块矩阵，且均为nN×n阶。因而有

δXi=WxiδX1

δΛi=WλiδΛ1

(41)

式中：Wxi和Wλi分别为矩阵Wx和矩阵Wλ的部分。则有

(42)

从而可得

(43)

基于最优轨迹的在线修正求解过程为：首先，采用文献[16]中的伪谱法计算最优参考轨迹X*(τ)和参考控制量U*(τ)，然后根据实际轨迹与最优参考轨迹的状态偏差量，通过邻域最优控制律计算获得LGR点处的修正控制量δu(τi)，节点处修正后的控制量为u(τi)=u*(τi)+δu(τi)，最后通过插值可获得整个轨迹修正后的控制量。

这种邻域最优控制算法在执行过程中不需要迭代运算和积分运算，只是进行矩阵运算，减小了计算量，具有较强的实时性。

2.3 初始偏差下的邻域最优控制律验证

针对上述的高超声速飞行器再入过程，首先生成最优参考轨迹，采用文献[16]中的分段Radau伪谱法进行计算，在联想CPU 3.4 GHz Intel Core i7计算机上运行，仿真结果如图1所示。

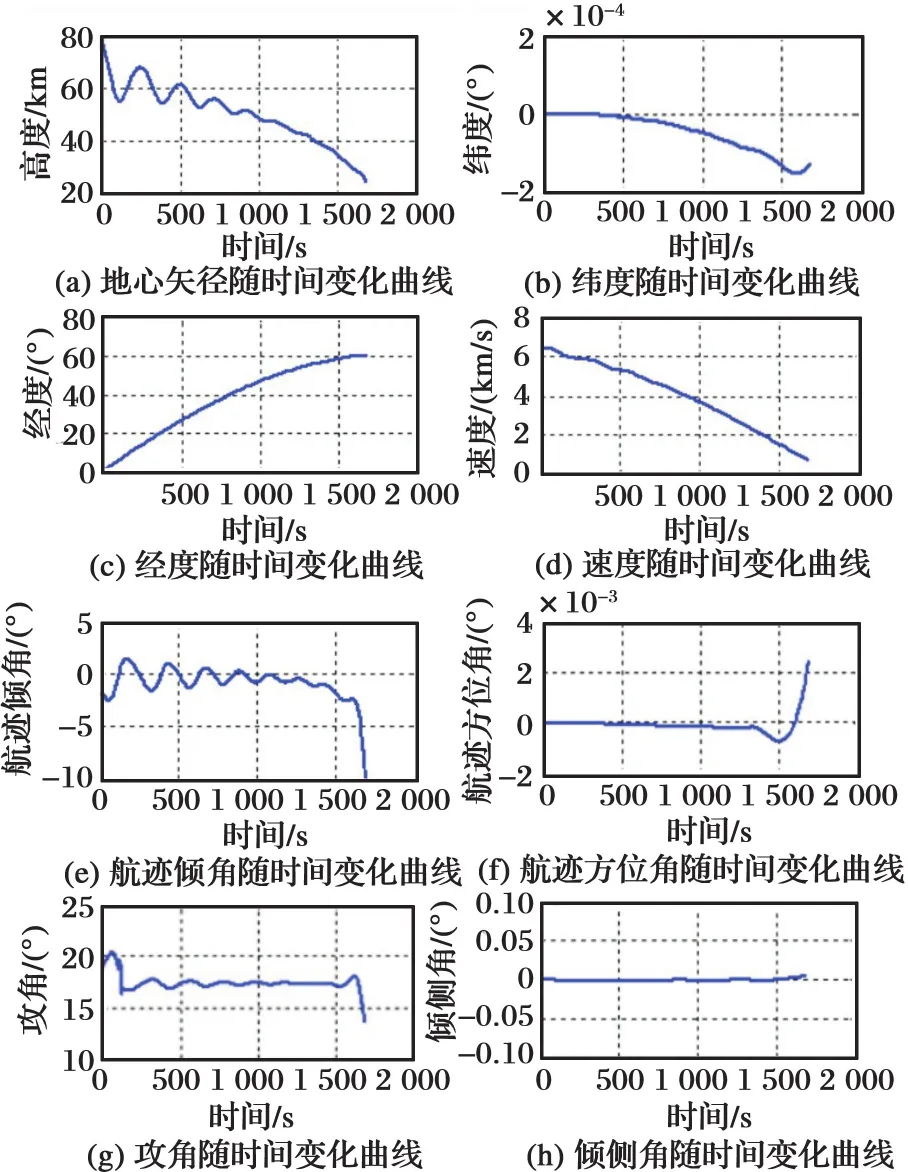
图1 基于分段Radau伪谱法的仿真结果Fig.1 Simulation results based on multi-stage Radau pseudospectral method

图1为飞行器飞行状态地心矢径、纬度、经度、速度、航迹倾角、航迹方位角以及控制变量攻角与倾侧角随时间变化的曲线。整个飞行过程为1 656 s，最终经度为60.56°，仿真计算时间为6.87 s。在给定的初始条件下，整个飞行中状态量及控制量满足各自的上下边界约束条件，飞行器最终状态满足给定的终端约束条件。

为了验证邻域最优控制律的有效性，令状态量初始扰动为|Δr(0)|≤1 000 m；|Δφ(0)|≤0.5°;|Δθ(0)|≤0.5°；|Δv(0)|≤100 m/s;|Δγ(0)|≤0.5°；|Δχ(0)|≤0.5°。

为了便于比较，令case 1和case 2分别为状态量初始扰动取最大正值和最大负值。close 1和close 2分别为扰动case 1和case 2时采用上述邻域最优控制律求得的修正控制量。与其对应，open 1和open 2分别为未采用邻域最优控制律求得的偏差量,仿真结果如图2所示。

图2 飞行器状态与标准参考轨迹的比较Fig.2 Comparison of aircraft state and standard reference trajectory

close 1和close 2的偏差量最终都趋近于零。而open 1和open 2中的偏差量均有较大值，且有的状态量的偏差绝对值逐渐增大。仿真结果表明，邻域最优控制律对飞行器初始状态量的较大范围偏差具有良好的鲁棒性。

考虑到整个再入过程中高超声速飞行器的热流密度、动压、过载等过程约束，分别设定Qmax=79.5 kW/m2，qmax=0.013 4 MN/m2，nmax=2.5g，验证如图3所示。图3中normal为初始状态量无扰动时采用文献[16]分段Radau伪谱法仿真的结果。close 1与close 2分别为初始扰动取case 1和case 2时采用邻域最优控制律仿真的结果。与其对应，open 1与open 2分别为未采用邻域最优控制律仿真的结果。

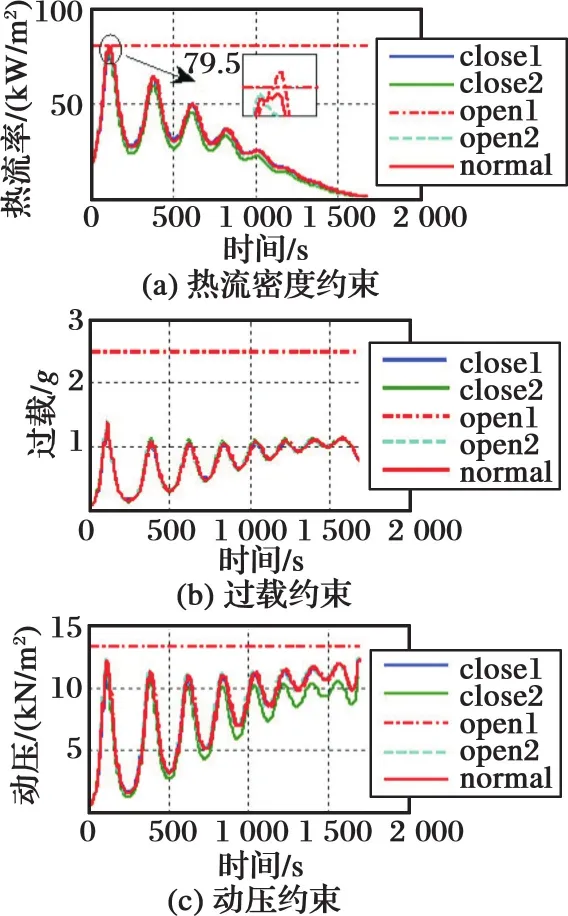
图3 过程约束情况Fig.3 The case of the process constraint

从图3可以看出，文献[16]方法对再入最优参考轨迹的求解是有效的。close 1与close 2曲线表明，存在初始状态量大范围扰动时的实际飞行轨迹满足动压、过载、热流等路径约束条件。open 1与open 2曲线表明，当不采用本文邻域最优控制律时，热流约束超过了限制值。仿真结果表明,本文设计的邻域最优控制律在最优轨迹跟踪中的有效性。

3 结 论

本文在多段Radau伪谱法生成最优参考轨迹的基础上，针对轨迹制导中存在初始扰动的问题，提出一种基于间接Radau伪谱法的邻域最优控制律，得出以下结论：

(1) 多段Radau伪谱法能够快速求解获得一条精确的再入最优轨迹，并满足路径约束条件及终端约束条件。

(2) 本文提出了基于Radau伪谱法的邻域最优控制律，对该制导律的性能进行了仿真验证。首先过程采用文献[16]中的分段Radau伪谱法获得了最优参考轨迹，然后验证了在状态量具有较大初始扰动的情况下，本文基于Radau伪谱法的邻域最优控制律可以在线修正最优参考轨迹，减少了初始扰动引起的偏差，证明了其具有良好的鲁棒性。通过进行矩阵运算，能够快速获得控制量的修正值，证明了其具有良好的实时性。

(3) 当终端约束条件发生变化，重新规划新的轨迹不能满足实时性要求时，如何通过邻域最优控制律使实际轨迹能够适应终端约束条件的变化，是下一步的研究内容。