基于ARIMA模型的制动摩擦衬片磨损预测
何晰浩 李金龙 郝占武 隋清海
(1. 中国第一汽车股份有限公司 研发总院,长春130013;2. 汽车振动噪声与安全控制综合技术国家重点实验室,长春130013)
主题词:摩擦衬片 ARIMA 磨损 制动
1 引言
随着国内汽车保有量的爆发式增长,交通事故的数量也随之升高。为了减少交通事故,降低人员伤亡,行车安全被越来越多的关注。汽车制动系统的制动器摩擦副在工作时产生摩擦阻力,将车辆行驶的机械能转化为热能,让车辆减速或者停车[1]。在能量转化的过程中,制动器摩擦衬片会出现磨损现象。当摩擦材料磨损到极限时,制动系统性能会下降甚至功能失效,影响汽车驾乘安全。因此摩擦材料的寿命预测显得非常重要。
汽车摩擦材料磨损性能试验是检验摩擦材料耐磨程度和预测整车寿命的检验方法,可分为摩擦材料小样试验、摩擦片台架试验和整车道路试验3种[2]。
摩擦材料小样试验具有简捷、快速、设备投资与试验费用低等优点[3],但通常小样试验只会在基础摩擦材料研发时进行,当摩擦材料应用到具体车型时,其磨损特性与车型惯量、摩擦材料形状、散热条件关系密切。摩擦片台架试验各个整车厂均有相关的台架试验方法,典型的有krauss 试验和惯性台架试验,惯性台架试验成本高,方法复杂,完整试验时间长。
整车道路试验常由整车厂进行,涵盖市区、高速、乡村、山路等工况,如美国的洛杉矶LACT试验以及西班牙Mojcar 试验等[4];虽然整车道路试验对摩擦衬片寿命预测准确,但试验耗时长,开发验证的时间较晚。
因此,需要建立摩擦衬片寿命的预测方法。王丽贤[5-7]等人指出,预测是指运用适当的手段搭建符合过去状态、当前水平和未来发展趋势的模型。传统的数据预测方法有回归分析预测法、灰色系统预测法、时间序列预测法等。李王宇辰[8]和张彦[9]利用灰色系统预测法对摩擦衬片的寿命进行预测,但预测精度有限。罗庆生[10]应用回归分析法对摩擦衬片的寿命进行预测,但缺乏工程应用价值。自回归求积移动平均模型(Auto Regressive Integrated Moving Average model,ARIMA)[11]是Box 和Jenkins 等在上个世纪七十年代提出的一种时间序列预测方法,能够排除扰动,不依赖外部变量、克服其他因素的影响,根据时间序列历史值对未来值进行预测[12],简称ARIMA 模型,是目前应用最广、精度最高的线性时间预测方法。
本文建立了一定时间范围内的摩擦片磨损量ARIMA模型。研究结果表明,该模型可以实现对摩擦片磨损趋势的预测,且预测精度较高,具有一定的工程应用价值。
2 ARIMA模型基本理论
当汽车制动时,摩擦衬片便会磨损,磨损量随着车辆的里程增加而随之增加,因此可以将摩擦衬片的磨损过程看作随时间变化而发展的时间序列,时间序列的观测值要求时间是等间隔的。从上个世纪二十年代起,陆续有学者开始研究时间序列并建立数学分析模型[12],时间序列模型包括自回归AR(p)模型、移动平均MA(q)模型、自回归移动平均ARMA(p,q)模型、自回归求积移动平均ARIMA(p,d,q)模型。
2.1 时间序列模型简介
2.1.1 自回归AR模型
如果一个时间序列{yt;t=1,2,…}只与该序列的历史数据有关,与其他因素无关。那么该时间序列可以用自回归(AR)模型进行预测。
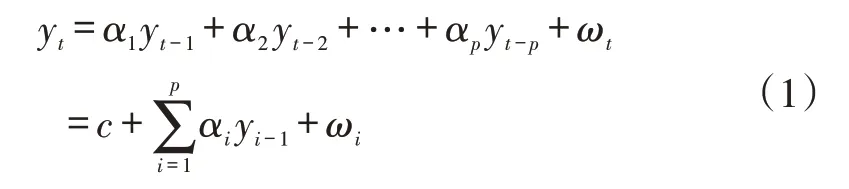
式中,p为自回归模型的阶数,记为AR(p),α和ω是回归系数,c为常数。
2.1.2 移动平均MA模型
如果一个时间序列{yt;t=1,2,…}可以用过去各个时期的随机干扰或预测误差的线性组合来表达当前预测值,那么可以用移动平均MA(q)模型进行预测。

式中,yi-1为t时刻和t-i时刻的随机误差,q表示模型的阶数,记为MA(q)。
2.1.3 自回归移动平均ARMA模型
如果一个时间序列{yt;t=1,2,…}既有自回归模型AR(p)和移动平均模型MA(q)的特点时,该序列可以用自回归移动平均ARMA模型进行预测。
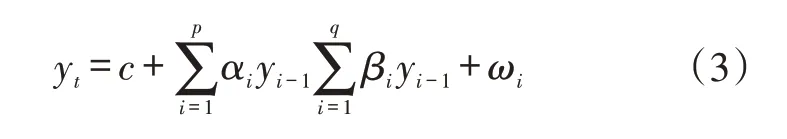
式(3)可以看作自回归模型AR(p)和移动平均模型MA(q)的组合,当p=0 时,模型表现为移动平均模型;当q=0 时,模型表现为自回归模型。
2.1.4 自回归求积移动平均ARIMA模型
如果时间序列是非平稳的,需要先对序列进行差分处理,将其转化为平稳序列后再使用ARMA(p,q)模型进行预测,即ARIMA(p,d,q)模型。模型中p表示自回归项数,d表示时间序列差分次数、q表示移动平均项数。
2.2 时间序列预测流程
时间序列的预测首先要以时间为标准收集一系列数据。其次对时间序列进行平稳性检验。对于平稳序列,应建立ARMA模型的识别,确定模型参数p值和q值;对于非平稳序列,要先通过d次差分得到平稳序列,再建立ARIMA 模型。模型建立之后,需要对其拟合效果进行检验,拟合效果较好的模型方可用于时间序列的预测。
3 ARIMA模型构建
3.1 ARIMA模型建模步骤
首先采集一组随时间变化的数据,应用Python或者EViews 等软件对数据进行平稳性检验。如果数据平稳,进行ARMA分析,确定p、q值;如果数据不平稳,则需要差分后再次进行平稳性检验,差分的次数是d值。最终建立差分后平稳序列的ARIMA模型,模型即可用于该序列的数据预测,图1是ARIMA建模流程。

图1 ARIMA模型预测流程
3.2 获取原始数据
根据徐仁泉等人的研究[13],为获取某摩擦片磨损量的下限与工作时间的试验数据,采用相同的工作时间间隔(5 h)检测得到的磨损量下限随时间的变化关系为研究对象。取前45 h的测量值为原始数据,对第50 h的磨损量进行预测,验证ARIMA模型的预测精度和可靠性(表1)。

表1 摩擦片磨损量下限与工作时间的数据
3.3 模型及参数的确定
3.3.1d值的确定
首先应用ADF 检验法查看时间序列的稳定性。ADF检验法假设时间序列存在单位根,即假设时间序列是不平稳的,存在周期性的波动。如果检验结果显示T值的绝对值低于1%、5%、10%的观测水平,并且显著概率P-value值大于0.05时,则认为序列不平稳,此时不能拒绝原假设。
表2给出了原始序列、一阶差分序列、二阶差分序列的ADF 检验结果,可以看出,原始序列T值的绝对值小于1%,5%,10%的观测水平,显著概率P-value值大于0.05,说明原始序列不平稳。一阶差分序列T值的绝对值大于5%,10%的观测水平,但小于1%的观测水平,说明当序列的置信度大于99%时,一阶差分序列不平稳。二阶差分序列的T值的绝对值大于1%水平的绝对值,且原假设的接受概率为0,证明了二阶差分序列平稳,故ARIMA模型的参数d取值为2。
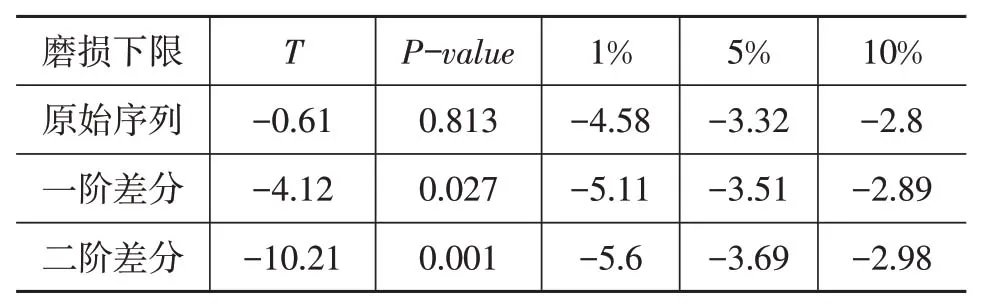
表2 ADF检验结果
3.3.2p值和q值的确定
ARIMA分析可以通过自相关图(ACF)和偏自相关图(PACF)来判断序列的大概范围。
如图2所示,经过数据处理可以看出,差分序列在自相关图一阶截尾,偏自相关图一阶拖尾,所以p值取1,q值取1。

图2 差分序列的自相关图和偏自相关图
因此,经过数据分析后,可以用ARIMA(1,2,1)对原始序列建模,进行模型预测和数据分析工作。
4 模型预测及分析
4.1 模型预测
对摩擦衬片磨损的序列建立ARIMA(1,2,1)的模型,建模参数如表3。拟合数据的R2达到0.997,证明拟合程度非常好,AR和MA的系数分别为0.429 和0.989,显著性水平都不为0。

表3 ARIMA(1,2,1)模型建模结果
表4给出了ARIMA模型的预测结果,第50 h的预测值与真实值相比,绝对残差为-4.17,相对残差为-1.67%,拟合精度达到了预测的要求。

表4 ARIMA模型预测结果
4.2 与其他预测方式的比较
与灰色数学预测方法的比较见表5,可以看出,ARIMA模型的预测数据更完整,预测精度更高。

表5 ARIMA模型与灰色数学模型比较
5 结论
通过实例分析可以看出,采集摩擦衬片的磨损量随时间变化的数据,建立的基于ARIMA 的摩擦衬片磨损量模型在工程上是可行的。
相比于残差修正的灰色数学模型,ARIMA模型具有更高较高的精度,更贴合工程实际,可以较为真实的反应摩擦衬片的随时间变化的磨损变化趋势,有助于相关从业者通过试验数据分析预测摩擦衬片的磨损寿命。
针对目前常用的制动器台架试验磨损方法,SAE J2707 中的method A 章节的试验数据,可以用本文介绍的方法进行分析,method B 章节block wear 的试验数据,更适合用非均匀采样数据的相关试验方法进行分析研究,笔者也将继续深入研究。

