基于光度立体和级数展开法的金属表面缺陷检测方法

朱勇建，罗 坚，秦运柏，秦国峰，唐楚柳

(广西师范大学 电子工程学院，广西 桂林 541004)

光度立体法[1]被广泛应用于农产品质量检测[2]、医疗诊断[3]、服装织物质量检测[4]等领域。将该技术应用于产品表面质量检测领域，可精确检出表面微小缺陷，具有分辨率高、受环境影响小、硬件成本低廉等特点。

黄秀玲等[5]提出一种基于光度立体法的药品泡罩包装中铝箔缺陷检测方法，该方法使用 4 个白光条形LED光源，从 4 个不同照射方向采集图像，利用光度立体法提取待测物表面梯度数据，再利用表面高斯曲率算法，完成缺陷检测；程耀瑜等[6]提出一种基于光度立体法的地板疵点检测方法，该方法同样使用 4 个白光条形LED光源采集图像，利用光度立体法突出地板表面的疵点特征，通过SVM分类器完成疵点检测与分类；刘根等[7]提出一种基于光度立体法的皮革缺陷检测方法，该方法使用 4 个柔性条形光源采集图像，利用光度立体法提取待测物表面反射率及曲率滤波图像，结合图像显著性[8]完成缺陷检测。但是，上述方法仅对具有近朗伯特性且有良好表面的物体检测时能取得较好的结果，而应用在金属表面缺陷检测时，则会存在严重的误检、漏检问题。

王磊等[9]提出一种基于光度立体法带钢表面缺陷三维检测方法，该方法使用红色、蓝色线激光光源对称分布于 3CCD线阵相机两侧，两光源以45°入射，同时照射同一目标区域，采集 1 幅彩色图像，再从彩色图像分离R、B颜色通道，利用光度立体法提取待测物梯度数据，使用积分算法，恢复待测物的三维形貌，以完成缺陷检测。但是，该方法光源参数的标定趋于理想化且操作复杂；三维重建时将x方向的梯度假设为零，仅利用y方向的梯度数据进行三维形貌恢复，如此一来，损失了x方向的信息；而且三维重构曲面也存在变形问题，影响缺陷的检测。Soukup等[10]结合卷积神经网络，提出一种基于光度立体法的金属表面缺陷检测方法，该方法也是使用红色、蓝色光源采集 1 幅彩色图像，根据卷积神经网络原理，训练5 000 个样品，以完成缺陷检测。但该方法样本量大且训练时间长，而且在实际应用时，较难获取样本。

为了解决机器视觉系统[11-12]对具有粗糙纹理的金属表面缺陷检测时出现误检、漏检，甚至无法检出的问题，本文提出使用光度立体法对金属表面进行三维重构，提取表面深度信息，根据深度信息实现缺陷检测，从而提高缺陷的检出率。本文对比了多种基于梯度数据的积分算法，选择了最能还原金属表面形貌的一种算法。同时，针对光度立体在金属表面三维形貌重构时存在重构曲面扭曲、翘曲等变形问题，提出一种基于级数展开的曲面拟合方法解决此问题，相较于曲面拟合前，检出率提高了4个百分点以上。本文中进行的仿真与实际实验均验证了所提算法在实际应用中具有一定的优越性与灵活性。

1 基于立体视觉的金属表面三维重构方法研究

本文金属表面三维形貌重构的流程如图 1 所示，详细步骤为：使用图像采集装置，采集待测金属表面不同光源照射方向下的 9 幅图像，利用已标定好的光源方向数据，通过构造偏微分方程[13]提取待测金属表面梯度；对梯度数据进行积分，获取待测金属表面的深度图；利用级数展开法原理拟合曲面，得到最终的待测金属表面三维形貌重构图。

图1 本文方法流程Fig. 1 Method flow of this article

1.1 光度立体法

经典光度立法是通过公式 (1) 构造线性方程组求解物体表面法向量。光度立体关键在于光度信息，因而光源方向的标定是首要的。文献[13]使用单采样球法，选择圆上的全部采样点参与计算，利用最小二乘法求解光源方向参数。本文光源标定算法与文献[13]有所区别：本文通过设置一个阈值，选择大于阈值的采样点参与计算，也能获得较为准确的光源方向参数，且减少了数据运算量，提高了计算效率。

Ii=ρLiN,i∈(1,k)，

(1)

式中：k是图像数量；ρ是物体表面的反射率；Ii是第i幅图像的灰度值；Li是第i幅图像的光源向量；N是物体的法向量。

光度立体法是利用不同光照方向的光度信息提取待测物体的梯度数据。文献[14]利用彩色图像，分离RGB颜色通道，通过光度比消除反射率，构造线性偏微分方程组，通过最小二乘估计的正规方程对深度直接进行求解。本文梯度提取方法与文献[14]有所区别：本文利用灰度图像信息，构造偏微分方程提取待测物梯度数据，再对梯度数据进行积分，得到深度信息。通过构造偏微分方程，有效避免了经典光度立体法由反射率求解法向量的误差积累，而且计算效率更快。而利用灰度图像信息有效避免了文献[14]从彩色图像分离RGB颜色通道时的信息缺失，且大大降低了数据运算量，提高了计算效率。本文偏微分方程组是根据灰度图像物体表面的反射率特性进行构建：

Ii(x,y)=ρ(x,y)LiN(x,y)，

(2)

Ij(x,y)=ρ(x,y)LjN(x,y)。

(3)

式中的Ii(x,y)、Ij(x,y)是第i幅图像和第j幅图像在(x,y)处的灰度值。式(2)与式(3)相比，同时化简有：

(Ii(x,y)×LjN(x,y)-Ij(x,y)×LiN(x,y))=0。

(4)

将式(4)再次化简，可转为用梯度表示的方程组，即：

(5)

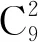
G=(WTW)-1WTU，

式中：

1.2 曲面重建算法

利用光度立体法提取待测物表面梯度数据后，为得到待测物表面三维形貌，需要对梯度数据进行积分。本文研究并分析了 7 种积分算法，其中包括Frankot-Chellappa算法[15]、Frankot-Chellappa-new算法[16]及SouthWell算法[17]，还分别使用 DCT、DST、FFT方式求解的泊松方程算法及Horn and Brooks算法[18-20]。依据重建效果，选择适合本文的一种曲面重建算法。

本文实验均是使用Intel(R) Core(TM) i5-3230M 2.60 GHz CPU，4.0 GiB RAM的Windows 10 64bit 计算机，同时使用MATLAB 2016b软件中的peaks函数模拟生成三维形状图，使用上述7种积分算法还原模拟三维形貌。图2显示了7种积分算法的重构曲面结果，直接观察进行分析，可知：使用DCT泊松算法、DST泊松算法、FFT泊松算法会存在变形问题；Horn and Brooks算法的还原性较差；Frankot-Chellappa算法、Frankot-chellappa-new算法及SouthWell算法能够较真实地还原模拟曲面形貌。因而采集实际场景中手机金属冲压片样品，可利用还原性较好的Frankot-Chellappa算法、Frankot-chellappa-new算法及SouthWell算法对梯度数据进行重构。图3是实际金属样品表面三维形貌结果图，所采用的3种积分算法均能表现金属表面形貌，但是，重建曲面存在扭曲及翘曲问题。表1是3种积分算法运行时间，实验中，在相同环境下，每种积分算法运行10次后取均值，得到算法运行时间。SouthWell算法迭代次数较多，因而花费的时间较长。根据还原性及算法运行时间，选择适合本文研究内容的Frankot-Chellappa积分算法。

根深蒂固的应试观念影响了高中生的思想教育，要改变这种现状，要认识到应试体制已不适应时代的发展要求。学校要树立新时代的人才培养观，要建立科学的思想教育管理体系，尽快推进应试教育向素质教育转变。要立足于人的发展，将人的素养提升置于首位，要重视学生潜能的发掘、个性的培养。

图2 模拟曲面三维形貌重构结果Fig. 2 Reconstruction result map of 3D topography of simulation surface

注：黑色框为手动标注缺陷位置。图3 实际金属样品表面三维形貌结果Fig. 3 3D morphology results of actual metal samples

表1 积分算法运行时间

1.3 级数展开法

光度立体法是基于理想的朗伯体反射模型，因而在实际应用时，很难满足理想的光照条件，尤其是在金属表面的三维形貌重建应用场景。利用光度立体原理恢复金属表面三维形貌时，重建曲面会出现扭曲及翘曲问题，本文针对此问题，提出了级数展开法的最小二乘法，可解决重建曲面出现的扭曲与翘曲问题，使得重建曲面更加接近实际物体形貌。具体步骤是：将重建曲面数据进行级数展开，利用最小二乘法求取多项式系数，再利用此系数重构曲面，得到无纹理光滑的曲面数据，最后将重构曲面数据减去无纹理光滑曲面数据，得到最终的重构曲面。

本文以 5 阶次进行级数展开为例说明。5 阶次方程是：

Z=p00+p10x+p01y+p20x2+p11xy+p02y2+

p30x3+p21x2y+p12xy2+p03y3+

p40x4+p31x3y+p22x2y2+p13xy3+p04y4+

p50x5+p41x4y+p32x3y2+p23x2y3+p14xy4+p05y5。

(6)

利用最小二乘法求解式(6)的系数，其转为矩阵形式

P=(MTM)-1MTS，

(7)

式中：

P=[p00,p10,p01,p20,p11,p02,p30,p21,p12,p03,p40,p31,p22,p13,p04,p50,p41,p32,p23,p14,p05]T；

M=[1,x,y,x2,xy,y2,x3,x2y,xy2,y3,x4,x3y,x2y2,xy3,y4,x5,x4y,x3y2,x2y3,xy4,y5]；

S=Z。

求取到系数P后，将其结合图像坐标重构无纹理光滑的曲面，最后将初次重构曲面减去无纹理光滑的曲面，得到接近真实重构曲面。

2 实验结果分析

2.1 金属表面三维形貌重构实验结果分析

图4 图像采集三维示意Fig. 4 3D image acquisition

采用本文所介绍的光度立体原理与级数展开法对所采集的仿真数据进行测试，同时对比不同阶次的拟合效果和结构相似性(SSIM)、均方误差及算法的计算时间，选择最合适的拟合阶次。对仿真数据进行三维形貌重建，重建曲面出现了扭曲和翘曲问题，其效果如图5(b)所示，将重建曲面进行曲面拟合，其拟合效果如图5(c)所示。本文对比了2阶次到15阶次的拟合效果，不同拟合阶次的结构相似性(SSIM)和均方误差如图6(a)所示，各阶次的计算时间如图6(b)所示。由图6可见，对于仿真数据的曲面拟合，虽然均方误差在4阶次时最小(均方误差为0.138 7，结构相似性为0.999 6)，但是在5阶次时，结构相似性(SSIM)和均方误差趋于稳定(均方误差为0.138 8)，4阶次和5阶次的均方误差仅相差0.000 1。因此，对于仿真数据的曲面拟合，选择 5 阶次是最合适的。

图5 模拟金属样品三维形貌重建效果Fig. 5 Reconstruction rendering of 3D topography of simulated metal samples

图6 仿真金属样品拟合效果衡量指标Fig. 6 Measurement index of fitting effect of simulated metal samples

在实际应用中，使用本文的实验装置采集手机金属冲压片图像，对其进行三维形貌重建，重建效果如图7(b)所示，同时，对其进行曲面拟合，拟合效果如图7(c)和(d)所示。对样品进行2阶次到15阶次拟合，其拟合效果衡量指标如图8所示。根据图8的指标分析，在8阶次时，结构相似性(SSIM)和均方误差趋于平缓，均方误差为0.263 5；在5阶次时，均方误差为0.316 3，两者的均方误差相差0.052 8。究其原因是因为采集图像的环境、采集图像的质量和噪声等干扰因素的影响。但是，实际应用时，需要考虑算法的计算时间，且考虑到计算时间是随着拟合阶次而递增的，5阶次和8阶次的计算时间相差2倍，因此，对于手机金属冲压片的曲面拟合，考虑到时间的评估指标，选择 5 阶次是较为合适的。

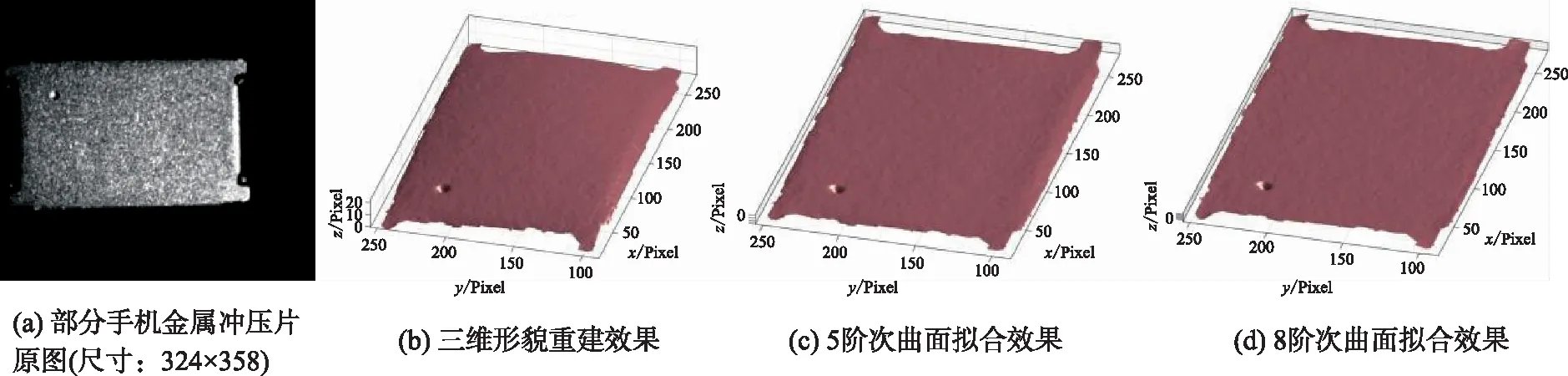
图7 手机金属冲压片三维形貌重建效果Fig. 7 3D shape reconstruction effect of metal stamping sheet of mobile phone

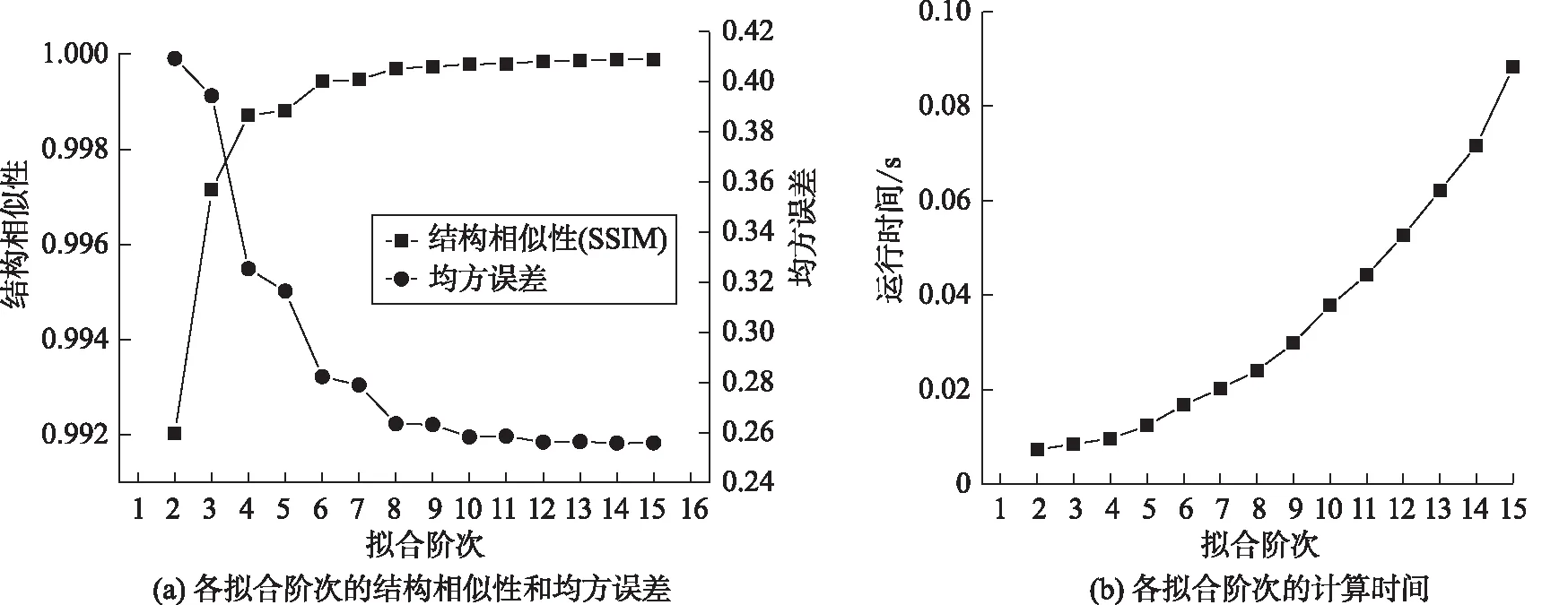
图8 手机金属冲压片拟合效果衡量指标Fig. 8 Measurement index for fitting effect of metal stamping sheet of mobile phone

此外，本文采用Zernike多项式[21-22]和级数展开算法重构目标三维形貌，并对重建效果进行对比分析。图9是使用3ds Max 2018仿真的实验效果。根据仿真实验结果分析，实验样品是具有粗糙金属特性的平面，但利用光度立体法重构后出现了扭曲及翘曲等变形现象。使用Zernike多项式进行曲面拟合和级数展开法拟合还原了金属表面真实的三维形貌。但是，Zernike多项式拟合曲面较为平滑，损失了部分图像信息，而级数展开法获得的图像细节信息更为丰富。

图9 模拟金属样品三维曲面拟合效果Fig. 9 3D surface fitting effect diagram of simulated metal sample

在与仿真场景相同条件下，根据图4(c)硬件装置采集金属硬币图像，同时采用本文算法对其进行三维形貌重建，并消除重建曲面变形问题，效果如图10所示。根据实际实验验证，使用Zernike多项式进行曲面拟合时，金属表面变得平滑，部分纹理信息缺失。如图11，使用Zernike多项式拟合的曲面，存在缺陷处对比度低的问题。

图10 五角硬币三维形貌重建效果Fig. 10 Rendering of the 3D shape reconstruction of Wujiao coin

图11 实际金属样品三维曲面拟合效果Fig. 11 3D surface fitting effect diagram of actual metal sample

综合上述实验分析可得，级数展开法解决了金属表面三维形貌重建时出现变形问题，还原了金属表面三维形貌。在对仿真数据测试时，5 阶次的算法计算效率比Zernike多项式算法的计算效率更高，详见表2。

表2 拟合算法运行时间

2.2 金属表面缺陷检测实验结果分析

使用本文设计的图像采集装置采集待测金属表面图像，并利用本文方法对其表面进行三维形貌重建。图12是缺陷检测流程，实现步骤是：首先对重建曲面采用级数展开法消除变形问题；其次使用已标定好的相机模型参数[23-24]将拟合后的曲面转为点云数据；接着对点云数据进行曲率滤波[25]处理；最后对滤波图像进行形态学处理[26]，实现缺陷的检测。实验中，选择了 3 种不同大小的手机金属冲压片样品进行缺陷检测实验，缺陷类型主要有凹坑、划痕及锈迹。表3是对手机金属冲压片样品的3种缺陷检出率的统计。图13中展示了实际金属样品的三维形貌重建效果、级数展开法拟合效果以及缺陷检测结果。

图12 缺陷检测流程Fig. 12 Defect detection flowchart

表3 本文方法缺陷检测结果

图13 实际金属样品缺陷检测Fig.13 Defect detection in actual metal samples

根据上述实验结果分析，重建曲面存在的变形问题会影响曲率计算，表面缺陷被凸显的同时也会引入较多干扰点，后续处理较为复杂。而级数展开法有效解决了因非朗伯特性及光照条件引起的重构曲面变形现象，解决了重构曲面扭曲及翘曲问题，拟合后曲面的曲率图能够清晰凸显缺陷特征，也降低了因翘曲而导致曲率突变的影响，更利于后续检测。对表3分析发现，在消除重建曲面变形问题前后，金属表面缺陷检出率均提高了4个百分点，其原因是：重建曲面存在变形问题，在对表面三维缺陷检测时，变形曲面影响检测，造成误检量和漏检量的提升，而拟合后的曲面更能凸显缺陷特征，从而降低了误检量和漏检量，因此，缺陷的检出率得到了提高。同时发现，5阶次和8阶次拟合后的缺陷检测结果一致，分析其原因是：对手机金属冲压片使用级数展开法拟合曲面后，金属表面缺陷细节信息保留在5阶次以上的曲面中，因此，更进一步验证了选择5阶次是较为合适的方案。

但是，将本文方法应用于手机金属冲压片表面缺陷检测时，对于凹坑缺陷的检出率是96.5%，划痕缺陷的检出率是76.2%，存在漏检和误检现象，其原因是：有些凹坑缺陷位于样品边缘，而样品边缘具有弧度的特点，在打光时边缘出现阴影和高反光的现象，在图像采集时，拍摄不到缺陷，影响到缺陷的检测；其次，因为凹坑缺陷分为中度、轻度凹坑，对于比较微小的轻度凹坑，在高斯曲率滤波后凸显不清晰；另外，对于划痕缺陷也分为中度、轻度划痕，对于比较细小的划痕，也会存在缺陷特征不明显的问题。本文方法能够对部分锈迹缺陷检测，其原因是：光度立体法是通过不同方向照射同一目标表面采集多幅图像，充分利用了图像亮度信息，而当金属表面出现大块锈迹时，会存在亮度较暗区域，对其提取梯度数据时，会出现较大误差，存在信息缺失，重建曲面出现严重形变，根据形变信息检测锈迹缺陷。但是，相较于机器视觉采用的良好打光方式，本文方法对锈迹的检出率较低，机器视觉方法的检出率较高。因此，在将金属表面缺陷检测方法应用于实际检测时，为提升缺陷检测率，会先使用机器视觉方法进行初步筛选，再使用三维缺陷检测方法解决机器视觉无法检测的问题。

综上所述，本文对于缺陷检测的方法较已有方法有一定的优势，但也存在不足，金属表面存在的高光和阴影是光度立体领域的难点与痛点。在本文实验中，使用单个LED光源，光照强度和单色性均会影响图像采集，实际应用时，使用单色性较好的光源，缺陷的检出率将会提升。

3 结语

本文通过光度立体和级数展开法还原金属表面三维形貌，解决了重建曲面存在扭曲及翘曲等变形问题，降低了因重建曲面变形导致的金属表面缺陷检测误差。本文针对金属表面缺陷检测，利用表面三维重构曲面的点云数据进行曲率滤波处理及形态学处理方式，完成缺陷检测，缺陷检出率均有所提高，算法鲁棒性更好。所提方法可应用于工业产品质量检测中，也可能推广至其他检测领域。本文所提的级数展开法虽然有效解决了因非朗伯特性及光照条件引起的重构曲面变形现象，但是该方法有其自身的适用性与局限性：该方法适用于测量对象为平整的金属表面；对于复杂曲面，该方法会消除复杂曲面本身的宏观形状。同时，所提检测方法对较浅划痕检出率还不理想，下一步将针对所述问题进行更加深入的研究及优化。